Topic semi perimeter of triangle: The semi perimeter of a triangle is a fundamental concept in geometry, representing half the perimeter of the triangle. It plays a crucial role in various geometric calculations, including Heron's formula for finding the area. Understanding the semi perimeter is essential for solving problems related to triangle measurements and properties.
Table of Content
- Semi Perimeter of Triangle
- Introduction
- Definition
- Formula
- Calculating Semi Perimeter
- Applications
- Properties of Semi Perimeter
- Using Semi Perimeter in Various Triangles
- Practice Problems
- Frequently Asked Questions
- YOUTUBE: Tìm hiểu về chu vi nửa của một tam giác, cách tính chu vi nửa của tam giác và công thức chu vi nửa của tam giác trong video này.
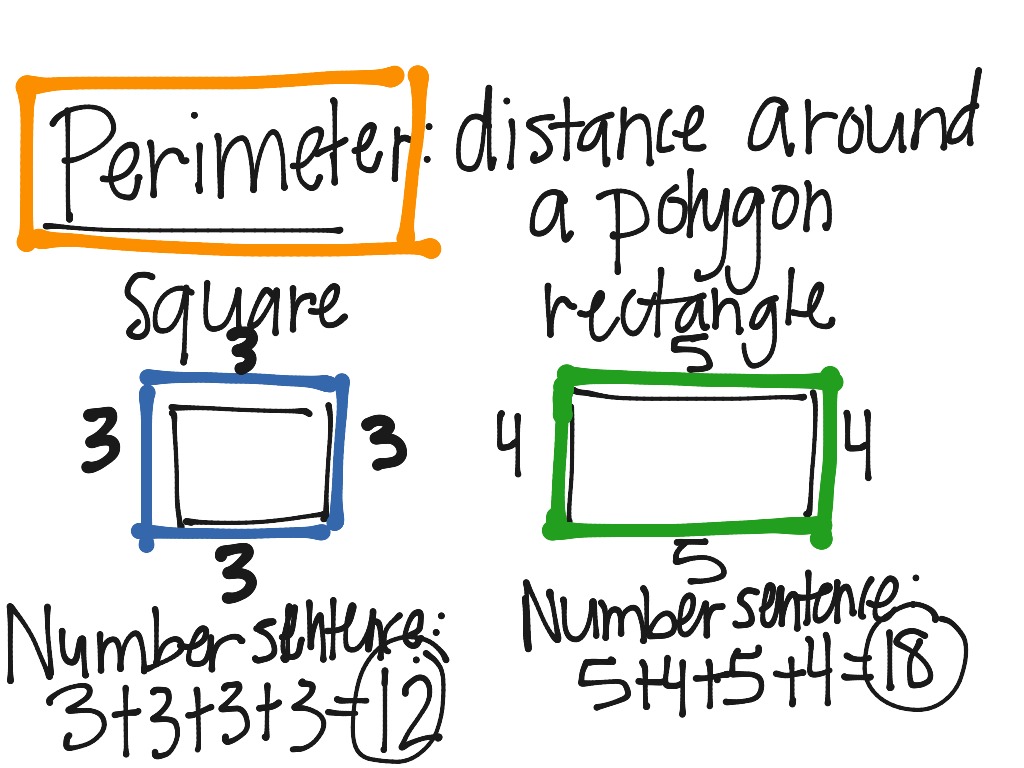
Semi Perimeter of Triangle
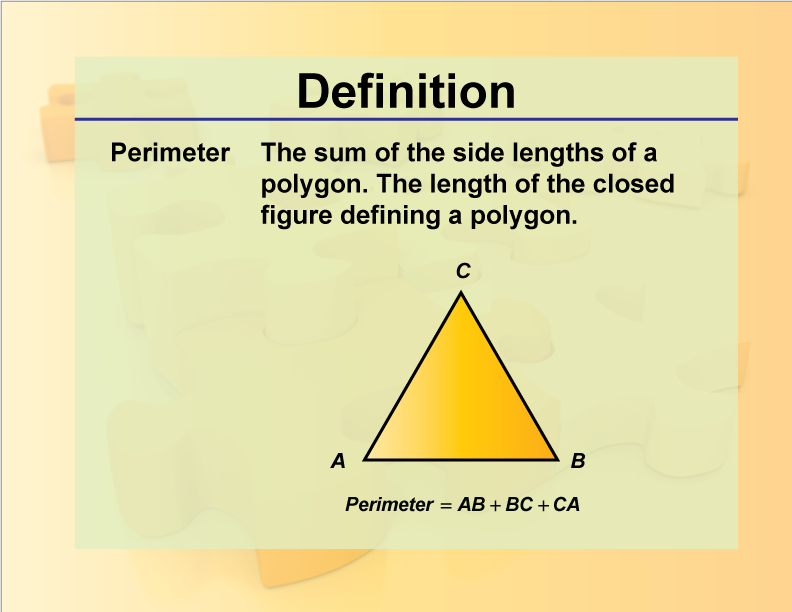
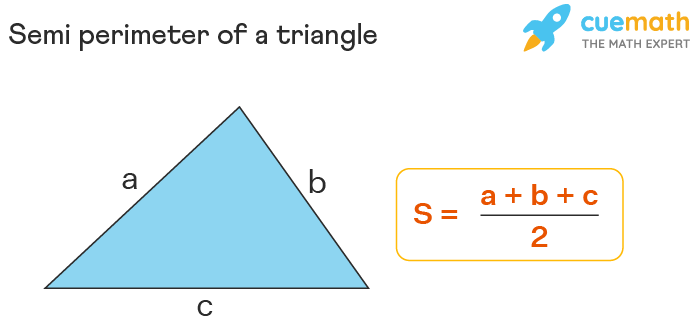
The semi perimeter of a triangle is defined as half of its perimeter. It is a significant value in various geometric calculations, particularly in Heron's formula for finding the area of a triangle. The semi perimeter is denoted by \(s\) and is calculated using the formula:
\( s = \frac{a + b + c}{2} \)
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Formulas for Semi Perimeter in Different Types of Triangles
| Type of Triangle | Formula | Explanation |
|---|---|---|
| Equilateral Triangle | \( \frac{3a}{2} \) | All sides are of equal length \(a\). |
| Isosceles Triangle | \( a + \frac{b}{2} \) | \(a\) is the length of the congruent sides, \(b\) is the base. |
| Scalene Triangle | \( \frac{a + b + c}{2} \) | All sides \(a\), \(b\), and \(c\) have different lengths. |
| Right Angle Triangle | \( \frac{base + height + hypotenuse}{2} \) | Using the base, height, and hypotenuse. |
Heron's Formula
Heron's formula allows us to find the area of a triangle when all three sides are known. The formula is expressed as:
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)
where \(s\) is the semi perimeter, and \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Examples
-
Example 1: Calculate the semi perimeter of a triangle with sides 15 units, 13 units, and 14 units.
Solution:
\( s = \frac{15 + 13 + 14}{2} = \frac{42}{2} = 21 \) units.
-
Example 2: Find the semi perimeter of an equilateral triangle with a side length of 16 units.
For an equilateral triangle, \( s = \frac{3a}{2} \). Here, \( a = 16 \) units, so:
\( s = \frac{3 \times 16}{2} = \frac{48}{2} = 24 \) units.
-
Example 3: Calculate the semi perimeter of an isosceles triangle with two sides of 7 cm and a base of 10 cm.
\( s = 7 + \frac{10}{2} = 7 + 5 = 12 \) cm.
Applications of Semi Perimeter
- Used in Heron's formula to calculate the area of a triangle.
- Helps in determining the inradius of a triangle.
- Useful in various geometric properties and theorems.
READ MORE:
Introduction
The semi-perimeter of a triangle is an essential concept in geometry and plays a crucial role in various mathematical formulas and applications. It is defined as half of the perimeter of the triangle, making it a valuable tool for simplifying and solving problems related to triangles.
Understanding the semi-perimeter helps in calculating the area of a triangle using Heron's formula and is also useful in various geometric properties and theorems. In this guide, we will explore the definition, formula, calculation methods, and applications of the semi-perimeter in detail.
Whether you are a student, a teacher, or a mathematics enthusiast, this comprehensive guide will provide you with a thorough understanding of the semi-perimeter and its significance in the study of triangles. Let's begin by diving into the definition and basic formula of the semi-perimeter.
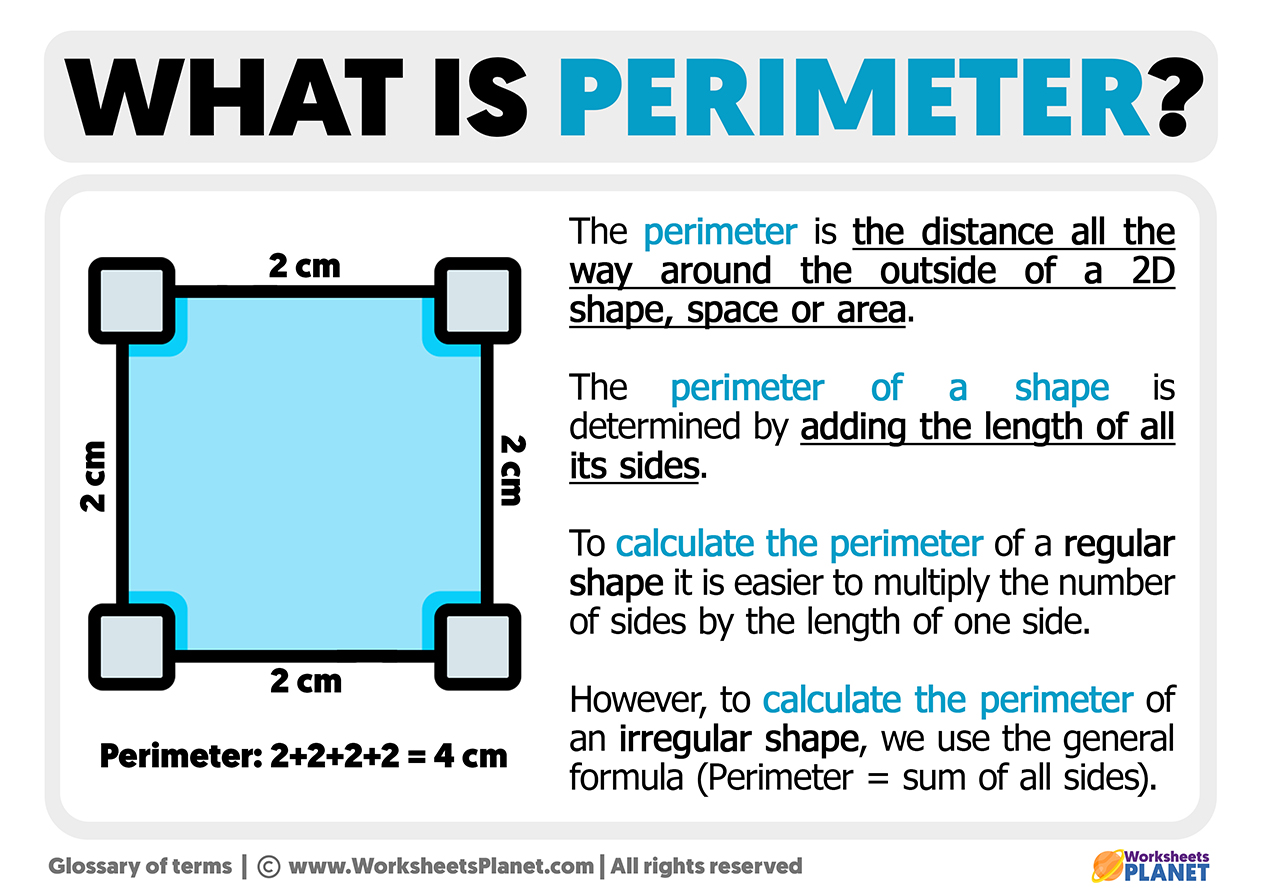
Definition
The semi-perimeter of a triangle is a key concept in geometry. It is defined as half of the perimeter of the triangle. The perimeter of a triangle is the total length of its three sides. Therefore, the semi-perimeter is calculated by summing the lengths of the three sides and then dividing the result by two.
Mathematically, the semi-perimeter s of a triangle with sides a, b, and c is expressed as:
\[ s = \frac{a + b + c}{2} \]
The semi-perimeter is an important measure because it is used in several key formulas in triangle geometry, including Heron's formula for finding the area of a triangle.
Example Calculation
Consider a triangle with side lengths of 14 cm, 8 cm, and 11 cm. The semi-perimeter s can be calculated as follows:
\[ s = \frac{14 + 8 + 11}{2} = \frac{33}{2} = 16.5 \, \text{cm} \]
Therefore, the semi-perimeter of this triangle is 16.5 cm.
The concept of semi-perimeter is not limited to triangles. It can also be applied to other polygons, although it is most commonly discussed in the context of triangles due to its use in Heron's formula.
Formula
The semi perimeter of a triangle is an important concept in geometry, particularly useful in various calculations such as finding the area using Heron's formula. The semi perimeter (\(s\)) of a triangle is defined as half of the perimeter of the triangle.
Given a triangle with side lengths \(a\), \(b\), and \(c\), the formula for the semi perimeter is:
\[ s = \frac{a + b + c}{2} \]
To illustrate, let's consider a triangle with sides of lengths 15 units, 13 units, and 14 units. The semi perimeter (\(s\)) is calculated as follows:
\[ s = \frac{15 + 13 + 14}{2} = \frac{42}{2} = 21 \, \text{units} \]
The semi perimeter is a fundamental value used in various geometric formulas, including Heron's formula for the area of a triangle. Heron's formula states that the area (\(A\)) of a triangle can be found using the semi perimeter (\(s\)) and the lengths of its sides (\(a\), \(b\), and \(c\)):
\[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
For example, to find the area of a triangle with sides of 21 units, 16 units, and 13 units, we first calculate the semi perimeter:
\[ s = \frac{21 + 16 + 13}{2} = 25 \, \text{units} \]
Using Heron's formula, the area is:
\[ A = \sqrt{25(25 - 21)(25 - 16)(25 - 13)} = \sqrt{25 \times 4 \times 9 \times 12} = \sqrt{10800} = 60 \sqrt{3} \, \text{square units} \]
Thus, the semi perimeter is not only a crucial intermediate step in these calculations but also a useful measure in its own right, often simplifying the expressions for further geometric analysis.
Calculating Semi Perimeter
The semi perimeter of a triangle is a crucial concept in geometry, often used in various calculations, including Heron's formula for finding the area of a triangle. The semi perimeter (denoted as s) is defined as half of the perimeter of the triangle.
To calculate the semi perimeter, follow these steps:
- Measure the lengths of all three sides of the triangle. Let these lengths be a, b, and c.
- Sum the lengths of the three sides to find the perimeter: \[ \text{Perimeter} = a + b + c \]
- Divide the perimeter by 2 to find the semi perimeter: \[ s = \frac{a + b + c}{2} \]
Here is a step-by-step example to illustrate the calculation:
- Consider a triangle with sides measuring 14 cm, 8 cm, and 11 cm.
- Calculate the perimeter: \[ \text{Perimeter} = 14 + 8 + 11 = 33 \text{ cm} \]
- Calculate the semi perimeter: \[ s = \frac{33}{2} = 16.5 \text{ cm} \]
Thus, the semi perimeter of this triangle is 16.5 cm.
Another example involves an equilateral triangle where all sides are equal. Suppose each side is 10 units:
- Calculate the perimeter: \[ \text{Perimeter} = 10 + 10 + 10 = 30 \text{ units} \]
- Calculate the semi perimeter: \[ s = \frac{30}{2} = 15 \text{ units} \]
Therefore, the semi perimeter of the equilateral triangle is 15 units.
Applications
The semi perimeter of a triangle has various practical applications, particularly in geometry and trigonometry. Here are some of the key uses:
- Heron's Formula: The semi perimeter is crucial in Heron's formula, which is used to find the area of a triangle when the lengths of all three sides are known. Heron's formula is given by:
\[ A = \sqrt{s(s-a)(s-b)(s-c)} \]
where \( s \) is the semi perimeter, and \( a \), \( b \), and \( c \) are the sides of the triangle. - Area of a Quadrilateral: Heron's formula can also be extended to find the area of a cyclic quadrilateral (a quadrilateral with all vertices on a circle). The semi perimeter is used in the formula for calculating the area of such quadrilaterals.
- Trigonometry: In trigonometry, the semi perimeter is used in various identities and calculations involving triangles, such as finding the radius of the inscribed circle (incircle) of the triangle.
- Engineering and Architecture: The semi perimeter is often used in engineering and architectural calculations to determine areas and other properties of triangular components in structures.
- Geographical Calculations: In geography, the semi perimeter is used in land surveying to calculate the area of triangular plots of land.
Overall, the concept of the semi perimeter is a fundamental tool in many fields that involve geometric and trigonometric calculations.
Properties of Semi Perimeter
The semi perimeter of a triangle, denoted as \(s\), is a fundamental concept in geometry with several useful properties and applications. Here are some key properties:
- Relation to Perimeter: The semi perimeter is exactly half of the triangle's perimeter. If \(a\), \(b\), and \(c\) are the side lengths of a triangle, then the semi perimeter \(s\) is given by: \[ s = \frac{a + b + c}{2} \]
- Heron's Formula: The semi perimeter is crucial in Heron's formula for finding the area of a triangle. Heron's formula states that the area \(A\) of a triangle can be calculated as: \[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
- Symmetry: The semi perimeter is symmetric with respect to the sides of the triangle, meaning it does not change if the sides are permuted.
- Half-Angle Formulas: The semi perimeter is used in trigonometric identities involving the half-angles of a triangle's internal angles. For example: \[ \sin \frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{bc}} \] \[ \cos \frac{A}{2} = \sqrt{\frac{s(s - a)}{bc}} \]
- Application in Other Formulas: The semi perimeter appears in various other geometric formulas and properties, such as in the calculation of the inradius \(r\) of a triangle: \[ r = \frac{A}{s} \] where \(A\) is the area of the triangle.
Understanding the semi perimeter is fundamental for solving many geometric problems, particularly those involving the calculation of areas and the application of trigonometric identities.
Using Semi Perimeter in Various Triangles
The concept of the semi-perimeter is widely used in various types of triangles, and its applications extend beyond simple calculations. Here are some specific uses and properties in different types of triangles:
- Equilateral Triangle: In an equilateral triangle, where all three sides are equal, the semi-perimeter simplifies the calculation of the area and other properties. The semi-perimeter \(s\) is equal to \( \frac{3a}{2} \), where \(a\) is the length of a side.
- Isosceles Triangle: For an isosceles triangle, which has two equal sides, the semi-perimeter helps in calculating the height and the area. The semi-perimeter \(s\) is \( \frac{2a + b}{2} \), where \(a\) is the length of the equal sides, and \(b\) is the base.
- Scalene Triangle: In a scalene triangle, where all sides are of different lengths, the semi-perimeter is crucial for using Heron's formula to find the area. The semi-perimeter \(s\) is \( \frac{a + b + c}{2} \), where \(a\), \(b\), and \(c\) are the lengths of the sides.
- Right Triangle: In a right-angled triangle, the semi-perimeter is used to find the radius of the excircle on the hypotenuse and to calculate the area more efficiently. The semi-perimeter \(s\) is \( \frac{a + b + c}{2} \), where \(c\) is the hypotenuse.
The semi-perimeter is also involved in various geometric properties and theorems, such as:
- Inradius and Circumradius: The semi-perimeter is used to calculate the inradius (\(r\)) and circumradius (\(R\)) of a triangle. The relationships are given by: \[ r = \frac{A}{s} \quad \text{and} \quad R = \frac{abc}{4A} \] where \(A\) is the area of the triangle.
- Medial Triangle: The semi-perimeter of a triangle is equal to the perimeter of its medial triangle, which is formed by connecting the midpoints of the sides of the original triangle.
- Splitters and Cleavers: In any triangle, the semi-perimeter can be used to describe splitters and cleavers, which are lines that partition the triangle into paths of equal lengths. These lines intersect at notable points like the Nagel point and the center of the Spieker circle.
Understanding the semi-perimeter and its properties allows for deeper insights into the geometry of triangles and aids in solving complex problems involving triangles.
Practice Problems
Here are some practice problems to help you understand and apply the concept of the semi-perimeter of a triangle:
-
Given a triangle with sides \( a = 7 \) cm, \( b = 24 \) cm, and \( c = 25 \) cm:
- Calculate the semi-perimeter \( s \).
- Use the semi-perimeter to find the area of the triangle using Heron's formula.
-
For an equilateral triangle with each side measuring 6 cm:
- Find the semi-perimeter.
- Calculate the area of the triangle.
-
A right-angled triangle has legs of 8 cm and 15 cm:
- Find the semi-perimeter of the triangle.
- Verify the area using the semi-perimeter and compare it with the direct calculation.
-
An isosceles triangle has a base of 10 cm and equal sides of 13 cm:
- Calculate the semi-perimeter.
- Determine the area using the semi-perimeter.
-
If the sides of a triangle are in the ratio 3:4:5 and its perimeter is 36 cm:
- Determine the lengths of the sides.
- Calculate the semi-perimeter.
- Find the area of the triangle.
These problems are designed to test your understanding of how to calculate the semi-perimeter and use it in various formulas. Ensure you practice thoroughly to gain confidence in these concepts.

Frequently Asked Questions
-
What is the Semi Perimeter of a Triangle?
The semi perimeter of a triangle is half the perimeter of the triangle. It is calculated as the sum of the lengths of the sides divided by 2. For a triangle with sides \(a\), \(b\), and \(c\), the semi perimeter \(s\) is given by the formula:
\[
s = \frac{a + b + c}{2}
\] -
How to Find the Semi Perimeter of a Triangle?
To find the semi perimeter of a triangle, add the lengths of all three sides and divide the sum by 2. For example, if the sides of a triangle are 4 units, 8 units, and 6 units, the semi perimeter is:
\[
s = \frac{4 + 8 + 6}{2} = \frac{18}{2} = 9 \text{ units}
\] -
Where is the Semi Perimeter of a Triangle Used?
The semi perimeter of a triangle is used in various formulas, including Heron's formula for finding the area of a triangle. Heron's formula is:
\[
\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}
\]where \(s\) is the semi perimeter and \(a\), \(b\), and \(c\) are the sides of the triangle.
-
What is the Semi Perimeter Formula for Different Types of Triangles?
- Equilateral Triangle: \[ s = \frac{3a}{2} \] where \(a\) is the side length.
- Isosceles Triangle: \[ s = a + \frac{b}{2} \] where \(a\) is the length of the two equal sides, and \(b\) is the length of the base.
- Scalene Triangle: \[ s = \frac{a + b + c}{2} \]
-
What is the Semi Perimeter of a Triangle with sides 40 cm, 24 cm, 32 cm?
To find the semi perimeter of a triangle with sides 40 cm, 24 cm, and 32 cm, use the formula:
\[
s = \frac{40 + 24 + 32}{2} = \frac{96}{2} = 48 \text{ cm}
\] -
How do you use the Semi Perimeter to Find the Area of a Triangle?
Using Heron's formula, you can find the area of a triangle when you know its sides. For a triangle with sides 21 units, 16 units, and 13 units, first calculate the semi perimeter:
\[
s = \frac{21 + 16 + 13}{2} = 25 \text{ units}
\]Then, use Heron's formula:
\[
\text{Area} = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{25(25-21)(25-16)(25-13)} = \sqrt{25 \times 4 \times 9 \times 12} = 60\sqrt{3} \text{ square units}
\]
Tìm hiểu về chu vi nửa của một tam giác, cách tính chu vi nửa của tam giác và công thức chu vi nửa của tam giác trong video này.
Chu vi nửa của một tam giác | Cách tìm chu vi nửa của tam giác | Công thức chu vi nửa của tam giác
READ MORE:
Video này cung cấp chứng minh trực quan về cách tính diện tích tam giác từ bán kính nội tiếp và chu vi nửa của tam giác.
Diện tích tam giác từ bán kính nội tiếp và chu vi nửa (chứng minh trực quan)