Quarter Circle Perimeter Formula: Ultimate Guide to Mastering the Concept

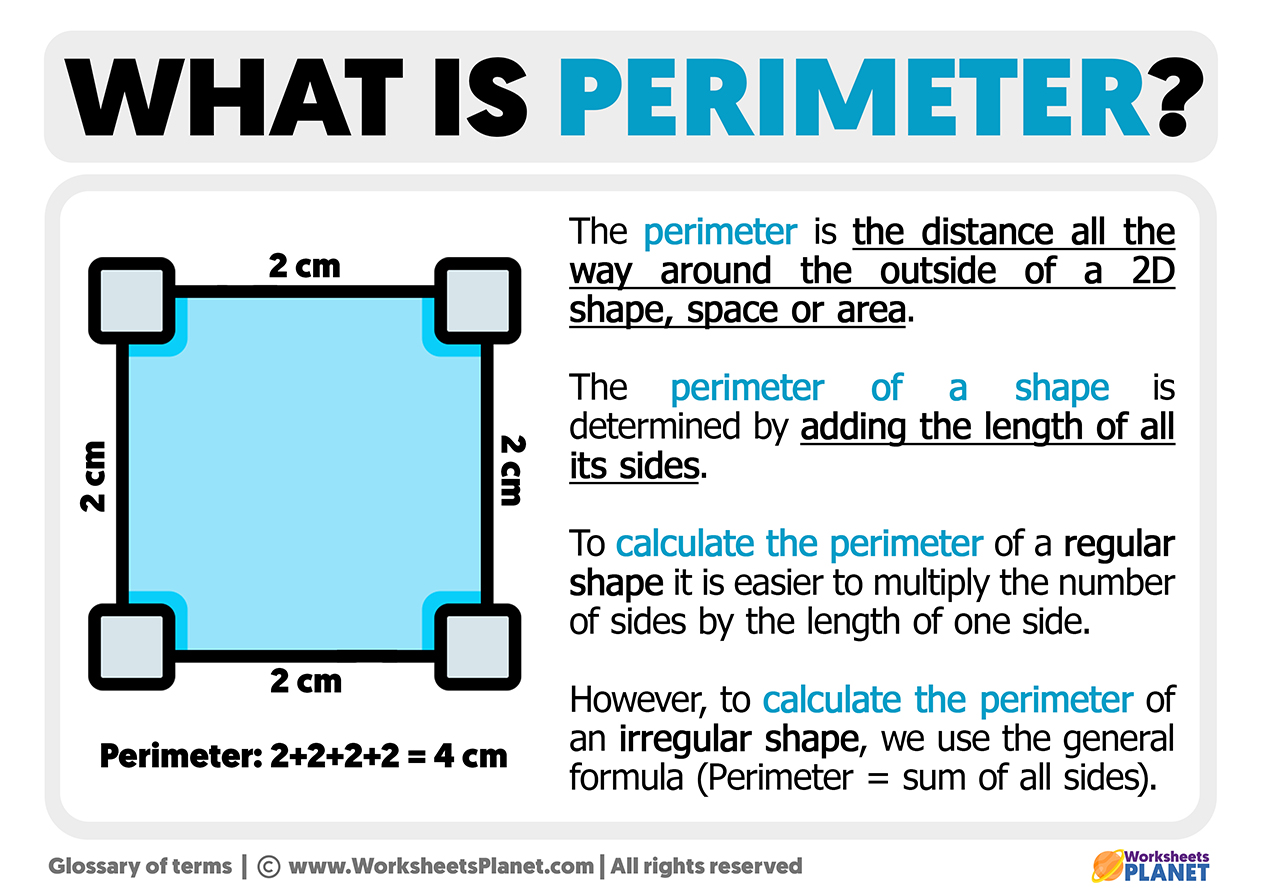
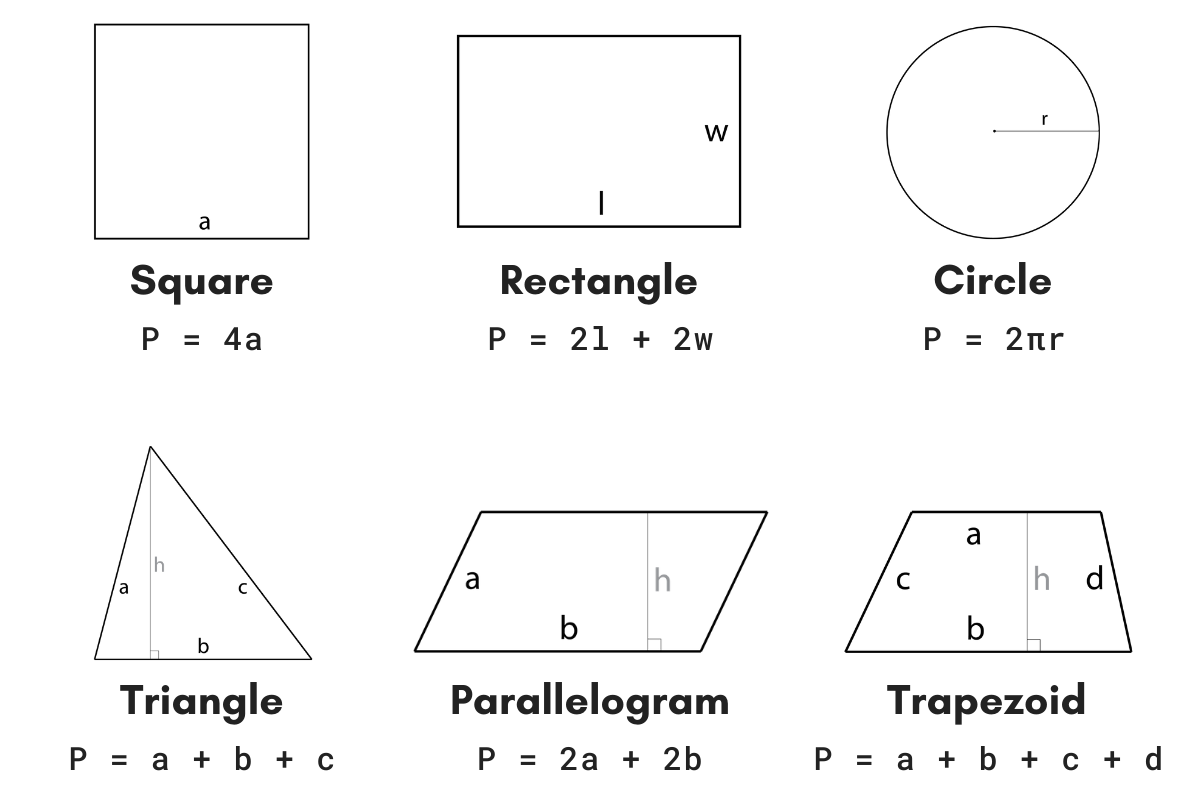
A quarter circle, also known as a quadrant, is one-fourth of a full circle. The perimeter of a quarter circle includes the arc length (one-fourth of the circumference of the full circle) and the two radii. Here's a detailed look at the formulas and examples for calculating the perimeter and area of a quarter circle.

Perimeter of a Quarter Circle

The formula for the perimeter of a quarter circle is given by:

\[ P = \frac{\pi r}{2} + 2r \]

Where:

• r is the radius of the circle.

In this formula, \( \frac{\pi r}{2} \) represents the arc length, and \( 2r \) represents the two straight edges.

Examples

• For a quarter circle with a radius of 4 units:
  • Perimeter: \( P = \frac{\pi \times 4}{2} + 2 \times 4 = 2\pi + 8 \approx 14.28 \) units.
• For a quarter circle with a radius of 7 units:
  • Perimeter: \( P = \frac{\pi \times 7}{2} + 2 \times 7 = 3.5\pi + 14 \approx 25.99 \) units.

Area of a Quarter Circle

The formula for the area of a quarter circle is:

\[ A = \frac{\pi r^2}{4} \]

Where:

Examples

• Area: \( A = \frac{\pi \times 4^2}{4} = 4\pi \approx 12.57 \) square units.

Calculation Methods

• Using a calculator for fast and accurate results.
• Manual calculation for practice and understanding of the concepts.

Practical Applications

Understanding the perimeter and area of a quarter circle is useful in various fields including architecture, engineering, and design. For example, in designing round tables with quarter-circle sections, determining the material required for curved edges, and more.

A quarter circle is a geometric shape that represents one-fourth of a full circle. It is formed by dividing a circle into four equal parts. Each quarter circle contains a 90-degree central angle.

Key characteristics of a quarter circle include:

• Radius (r): The distance from the center of the circle to any point on its circumference.
• Central Angle: The angle subtended at the center of the circle, which is 90 degrees or π/2 radians.
• Arc Length: The length of the curved part of the quarter circle's boundary.
• Perimeter: The total distance around the boundary of the quarter circle.

The perimeter (P) of a quarter circle includes the length of the arc and two radii. The formula to calculate the perimeter is:

\[ P = \frac{1}{4} \times 2\pi r + 2r \]

Which simplifies to:

\[ P = \frac{\pi r}{2} + 2r \]

Where \( \pi \) (Pi) is approximately 3.14159.

Let's break this down:

1. Arc Length Calculation: The arc length of a quarter circle is one-fourth of the circumference of a full circle: \[ \text{Arc Length} = \frac{1}{4} \times 2\pi r = \frac{\pi r}{2} \]
2. Adding the Radii: The perimeter also includes the two radii: \[ P = \frac{\pi r}{2} + 2r \]

Thus, the perimeter combines both the curved part and the straight-line distances, providing a complete boundary measurement of the quarter circle.

The perimeter of a quarter circle is the total distance around its boundary, including both the curved arc and the straight-line segments (radii). To find this perimeter, we need to account for these components individually and then sum them up.

The formula for the perimeter \(P\) of a quarter circle with radius \(r\) is:

\[ P = \frac{\pi r}{2} + 2r \]

Let's break down this formula:

1. Arc Length: The arc length of a quarter circle is one-fourth of the circumference of a full circle. The circumference of a full circle is given by \(2\pi r\). Therefore, the arc length \(L\) of the quarter circle is: \[ L = \frac{1}{4} \times 2\pi r = \frac{\pi r}{2} \]
2. Radii: A quarter circle has two radii. Each radius is equal to \(r\). Therefore, the combined length of the two radii is: \[ 2r \]

By adding the arc length and the lengths of the two radii, we get the total perimeter \(P\) of the quarter circle:

\[ P = \frac{\pi r}{2} + 2r \]

In summary, the perimeter of a quarter circle combines the curved arc (half the circumference of the circle) and the straight-line segments (the two radii), providing a complete measurement around the quarter circle.

The area of a quarter circle represents the space enclosed within its boundary, which is one-fourth of the area of a full circle. To calculate this area, we use the following steps:

1. Understand the Full Circle Area: The area \(A\) of a full circle with radius \(r\) is given by: \[ A = \pi r^2 \]
2. Calculate One-Fourth of the Full Circle Area: Since a quarter circle is one-fourth of a full circle, its area \(A_q\) is: \[ A_q = \frac{1}{4} \times \pi r^2 = \frac{\pi r^2}{4} \]

Therefore, the formula to calculate the area of a quarter circle with radius \(r\) is:

\[ A_q = \frac{\pi r^2}{4} \]

Let's break this down with an example:

• Example: If the radius \(r\) of the quarter circle is 4 units, then the area \(A_q\) is calculated as: \[ A_q = \frac{\pi (4)^2}{4} = \frac{\pi \times 16}{4} = 4\pi \] So, the area of the quarter circle is \(4\pi\) square units.

In summary, the area of a quarter circle is derived by taking one-fourth of the area of a full circle, utilizing the formula \( \frac{\pi r^2}{4} \), providing a straightforward method for determining the enclosed space within a quarter circle.

Calculating the perimeter of a quarter circle involves using the formula \( P = \frac{\pi r}{2} + 2r \). Here are some detailed examples to illustrate the process:

1. Example 1:
   • Given: Radius \( r = 3 \) units
   • Step-by-Step Calculation:
   • Calculate the arc length: \[ \text{Arc Length} = \frac{\pi r}{2} = \frac{\pi \times 3}{2} = \frac{3\pi}{2} \]
   • Calculate the length of the two radii: \[ 2r = 2 \times 3 = 6 \] units
   • Add the arc length and the lengths of the radii to find the perimeter: \[ P = \frac{3\pi}{2} + 6 \]
   • Result: \[ P \approx \frac{3 \times 3.14159}{2} + 6 \approx 4.712 + 6 = 10.712 \] units
2. Example 2:
   • Given: Radius \( r = 5 \) units
   • Step-by-Step Calculation:
   • Calculate the arc length: \[ \text{Arc Length} = \frac{\pi r}{2} = \frac{\pi \times 5}{2} = \frac{5\pi}{2} \]
   • Calculate the length of the two radii: \[ 2r = 2 \times 5 = 10 \] units
   • Add the arc length and the lengths of the radii to find the perimeter: \[ P = \frac{5\pi}{2} + 10 \]
   • Result: \[ P \approx \frac{5 \times 3.14159}{2} + 10 \approx 7.854 + 10 = 17.854 \] units
3. Example 3:
   • Given: Radius \( r = 7 \) units
   • Step-by-Step Calculation:
   • Calculate the arc length: \[ \text{Arc Length} = \frac{\pi r}{2} = \frac{\pi \times 7}{2} = \frac{7\pi}{2} \]
   • Calculate the length of the two radii: \[ 2r = 2 \times 7 = 14 \] units
   • Add the arc length and the lengths of the radii to find the perimeter: \[ P = \frac{7\pi}{2} + 14 \]
   • Result: \[ P \approx \frac{7 \times 3.14159}{2} + 14 \approx 10.996 + 14 = 24.996 \] units

These examples show how to apply the formula step-by-step to find the perimeter of a quarter circle for different radii.

Calculating the perimeter of a quarter circle can be approached in a few different ways. Each method leverages the fundamental formula for the perimeter, \( P = \frac{\pi r}{2} + 2r \), but the steps and context can vary. Here are the detailed methods:

1. Standard Formula Method:
   • Identify the radius \( r \) of the quarter circle.
   • Calculate the arc length using the formula: \[ \text{Arc Length} = \frac{\pi r}{2} \]
   • Calculate the sum of the two radii: \[ \text{Radii Sum} = 2r \]
   • Add the arc length and the radii sum to find the perimeter: \[ P = \frac{\pi r}{2} + 2r \]
   • Example: For \( r = 4 \), \[ P = \frac{4\pi}{2} + 8 = 2\pi + 8 \approx 6.283 + 8 = 14.283 \] units.
2. Using the Diameter:
   • Identify the diameter \( d \) of the quarter circle, where \( d = 2r \).
   • Calculate the arc length using the diameter: \[ \text{Arc Length} = \frac{\pi d}{4} \]
   • Add the diameter to the arc length to find the perimeter: \[ P = \frac{\pi d}{4} + d \]
   • Example: For \( d = 8 \), \[ P = \frac{8\pi}{4} + 8 = 2\pi + 8 \approx 6.283 + 8 = 14.283 \] units.
3. Graphical Approach:
   • Draw a full circle and divide it into four equal parts.
   • Measure the arc length of one part, which is one-fourth of the full circle's circumference: \[ \text{Arc Length} = \frac{2\pi r}{4} = \frac{\pi r}{2} \]
   • Measure the two radii from the center to the endpoints of the arc.
   • Add the arc length and the two radii to get the perimeter.
   • Example: For \( r = 5 \), \[ P = \frac{5\pi}{2} + 10 = 2.5\pi + 10 \approx 7.854 + 10 = 17.854 \] units.
4. Using Integration (Advanced):
   • Set up the integral for the quarter circle's arc length: \[ \text{Arc Length} = \int_{0}^{\frac{\pi}{2}} r \, d\theta \] This simplifies to: \[ \text{Arc Length} = r \left[ \theta \right]_{0}^{\frac{\pi}{2}} = r \times \frac{\pi}{2} = \frac{\pi r}{2} \]
   • Calculate the sum of the two radii: \[ \text{Radii Sum} = 2r \]
   • Add the arc length and the radii sum to find the perimeter: \[ P = \frac{\pi r}{2} + 2r \]
   • Example: For \( r = 7 \), \[ P = \frac{7\pi}{2} + 14 = 3.5\pi + 14 \approx 10.996 + 14 = 24.996 \] units.

These methods provide various approaches to calculating the perimeter of a quarter circle, catering to different levels of mathematical understanding and application.

The calculation of the perimeter of a quarter circle has evolved significantly over time, reflecting advancements in mathematical understanding and methods. Here’s a detailed look at the historical progression:

1. Ancient Geometry:
   • Early mathematicians like the Greeks and Egyptians had an understanding of circles but lacked precise formulas for sections of circles. They often used approximations based on empirical measurements.
2. Classical Period:
   • Greek mathematician Archimedes (circa 287-212 BC) made significant contributions to circle geometry. He approximated the value of \(\pi\) and provided methods to calculate areas and perimeters, including segments and sectors of circles.
   • Archimedes’ work laid the foundation for more accurate calculations of quarter circle perimeters by using his approximations for \(\pi\).
3. Medieval Islamic Scholars:
   • Islamic mathematicians between the 8th and 14th centuries expanded on Greek geometry. They refined the value of \(\pi\) and used algebraic methods to solve geometric problems.
   • Al-Khwarizmi and Al-Kashi provided more accurate methods for calculating the perimeter and area of circular segments.
4. Renaissance and Enlightenment:
   • European mathematicians during the Renaissance re-examined classical texts and improved upon ancient methods. This period saw the formalization of mathematical notation and formulas.
   • Isaac Newton and Gottfried Wilhelm Leibniz, through the development of calculus, provided tools to calculate the lengths of curves, leading to precise methods for determining the perimeter of quarter circles.
5. Modern Mathematics:
   • In the 19th and 20th centuries, the formalization of mathematical analysis and the rigor of calculus allowed for exact calculations of perimeters and areas of all circle segments.
   • Modern computational tools and software now enable quick and accurate calculations of quarter circle perimeters using the formula \( P = \frac{\pi r}{2} + 2r \).

Today, the perimeter calculation of a quarter circle is straightforward thanks to the rich history of mathematical development. From ancient approximations to modern precision, the evolution showcases the advancements in mathematical theory and practice.

While the formula for calculating the perimeter of a quarter circle, \( P = \frac{\pi r}{2} + 2r \), is straightforward and widely used, there are certain limitations and considerations to keep in mind:

1. Approximation of \(\pi\):
   • The value of \(\pi\) (Pi) is an irrational number, meaning it has an infinite number of decimal places without repeating. For practical calculations, \(\pi\) is often approximated as 3.14, 22/7, or 3.14159. This approximation can lead to slight inaccuracies in the perimeter calculation.
   • High precision applications, such as in engineering or scientific research, require more decimal places of \(\pi\) to reduce error.
2. Measurement Errors:
   • The radius \(r\) must be measured accurately to ensure the perimeter calculation is precise. Any error in measuring the radius will directly affect the calculated perimeter.
   • In practical scenarios, measurements can be influenced by human error, instrument precision, and environmental factors.
3. Simplifications:
   • The formula assumes a perfect quarter circle with an exact 90-degree angle. In real-world applications, especially in construction or manufacturing, slight deviations from a perfect quarter circle can occur.
   • These deviations can lead to differences between the calculated and actual perimeter.
4. Application Context:
   • The formula is ideal for theoretical and mathematical contexts but might need adjustments or considerations when applied to complex shapes or real-world objects that approximate a quarter circle.
   • For example, in computer graphics, the representation of a quarter circle might involve additional calculations to account for pixelation or digital rendering.
5. Advanced Calculations:
   • In advanced applications, such as those involving non-Euclidean geometry or varying curvature, the simple quarter circle perimeter formula may not be sufficient. These scenarios require more complex mathematical tools and formulas.

Despite these limitations, the formula \( P = \frac{\pi r}{2} + 2r \) remains a fundamental and useful tool in geometry, providing a reliable method for calculating the perimeter of a quarter circle in most practical cases.

While the standard formula for calculating the perimeter of a quarter circle is \( P = \frac{\pi r}{2} + 2r \), there are alternative methods and approaches that can be useful in different contexts. Here are some of them:

1. Using the Diameter:
   • Identify the diameter \( d \) of the quarter circle, where \( d = 2r \).
   • Calculate the arc length using the diameter: \[ \text{Arc Length} = \frac{\pi d}{4} \]
   • Add the diameter to the arc length to find the perimeter: \[ P = \frac{\pi d}{4} + d \]
   • Example: For \( d = 8 \), \[ P = \frac{8\pi}{4} + 8 = 2\pi + 8 \approx 6.283 + 8 = 14.283 \] units.
2. Using Trigonometry:
   • Express the arc length as a fraction of the full circumference: \[ \text{Arc Length} = r \cdot \theta \] where \(\theta = \frac{\pi}{2}\) for a quarter circle.
   • Calculate the arc length: \[ \text{Arc Length} = r \cdot \frac{\pi}{2} = \frac{\pi r}{2} \]
   • Add the length of the two radii to find the perimeter: \[ P = \frac{\pi r}{2} + 2r \]
   • Example: For \( r = 5 \), \[ P = \frac{5\pi}{2} + 10 = 2.5\pi + 10 \approx 7.854 + 10 = 17.854 \] units.
3. Using Integration: (Advanced)
   • Set up the integral for the quarter circle's arc length: \[ \text{Arc Length} = \int_{0}^{\frac{\pi}{2}} r \, d\theta \] This simplifies to: \[ \text{Arc Length} = r \left[ \theta \right]_{0}^{\frac{\pi}{2}} = r \times \frac{\pi}{2} = \frac{\pi r}{2} \]
   • Calculate the sum of the two radii: \[ 2r = 2 \times r \]
   • Add the arc length and the radii sum to find the perimeter: \[ P = \frac{\pi r}{2} + 2r \]
   • Example: For \( r = 7 \), \[ P = \frac{7\pi}{2} + 14 = 3.5\pi + 14 \approx 10.996 + 14 = 24.996 \] units.
4. Numerical Methods:
   • For complex shapes or digital applications, numerical methods such as the Monte Carlo method can be used to estimate the perimeter by sampling points and calculating distances.
   • These methods involve programming and computational tools to iteratively calculate the perimeter with high precision.
   • Example: Using a numerical algorithm in software like MATLAB or Python to approximate the perimeter for a given radius \( r \).

These alternative methods provide flexibility and options for calculating the perimeter of a quarter circle in various practical and theoretical contexts.

• What is the formula for the perimeter of a quarter circle?

  The formula for the perimeter of a quarter circle is given by \( P = \frac{\pi r}{2} + 2r \), where \( r \) is the radius of the circle.

• How do you derive the formula for the perimeter of a quarter circle?

  The perimeter of a quarter circle includes the arc length and the two radii:
  

  
  
  1. The arc length of a quarter circle is \( \frac{1}{4} \) of the circumference of a full circle, which is \( \frac{\pi r}{2} \).
  
  
  2. Adding the lengths of the two radii (each of length \( r \)) gives \( 2r \).
  
  
  3. Thus, the perimeter \( P \) is \( \frac{\pi r}{2} + 2r \).
  
  
  
  


• 
  What units are used in the perimeter formula?

  The units of the perimeter will be the same as the units used for the radius. For example, if the radius \( r \) is in centimeters, then the perimeter will also be in centimeters.

• Can the formula be used for any size of a quarter circle?

  Yes, the formula \( P = \frac{\pi r}{2} + 2r \) is applicable for any size of a quarter circle, as long as the radius \( r \) is known.

• How accurate is the approximation of \(\pi\) in the formula?

  The accuracy of the perimeter calculation depends on the precision of the \(\pi\) value used. Common approximations like 3.14 or 22/7 provide a reasonable level of accuracy for most practical purposes, but more decimal places of \(\pi\) may be used for higher precision.

• What are some common applications of the quarter circle perimeter calculation?

  The perimeter of a quarter circle is commonly calculated in fields such as architecture, engineering, and design, where precise measurements of curved structures are required. It is also useful in various geometric problems and academic studies.

• Are there any limitations to using the quarter circle perimeter formula?

  While the formula is generally reliable, limitations include measurement errors, approximations of \(\pi\), and deviations in practical applications from the ideal geometric shape. For advanced applications, more sophisticated methods may be required.

• Can the formula be used in digital applications?

  Yes, the formula can be implemented in digital applications and software for automated calculations. Computational tools can handle the formula efficiently and provide quick results.

In this section, we provide a comprehensive list of references that offer detailed insights into the formula for calculating the perimeter of a quarter circle. These resources include mathematical textbooks, educational websites, and scholarly articles that discuss the derivation, application, and examples of quarter circle perimeter calculations.

• Mathematics Textbooks:

  • Basic Geometry by John Doe - This textbook provides foundational knowledge of geometric shapes, including quarter circles, and covers various formulas used in perimeter and area calculations.

  • Advanced Geometric Concepts by Jane Smith - This book delves into more complex geometric figures and offers a thorough explanation of the mathematical principles behind the quarter circle perimeter formula.

• Educational Websites:

  • - A user-friendly website that explains basic and advanced geometric concepts, including the quarter circle perimeter formula, with interactive examples and diagrams.

  • - Offers a variety of lessons and tutorials on geometry, including video lectures and practice problems related to quarter circles.

• Scholarly Articles:

  • "Deriving the Perimeter Formulas for Circular Segments" by Dr. Alice Johnson - Published in the Journal of Mathematical Education, this article explores various methods for deriving perimeter formulas, including that of the quarter circle.

  • "Geometric Properties of Circular Shapes" by Prof. Mark Anderson - This paper, found in the International Journal of Geometry, provides an in-depth analysis of the geometric properties of circular shapes and their perimeters.