Topic kite perimeter formula: The perimeter of a kite is a fundamental concept in geometry, defined as the total distance around its edges. By understanding the kite perimeter formula, you can easily calculate this value, making it a crucial skill for students and enthusiasts alike. Explore the key properties and examples to master the calculations and enhance your geometry knowledge.
Table of Content
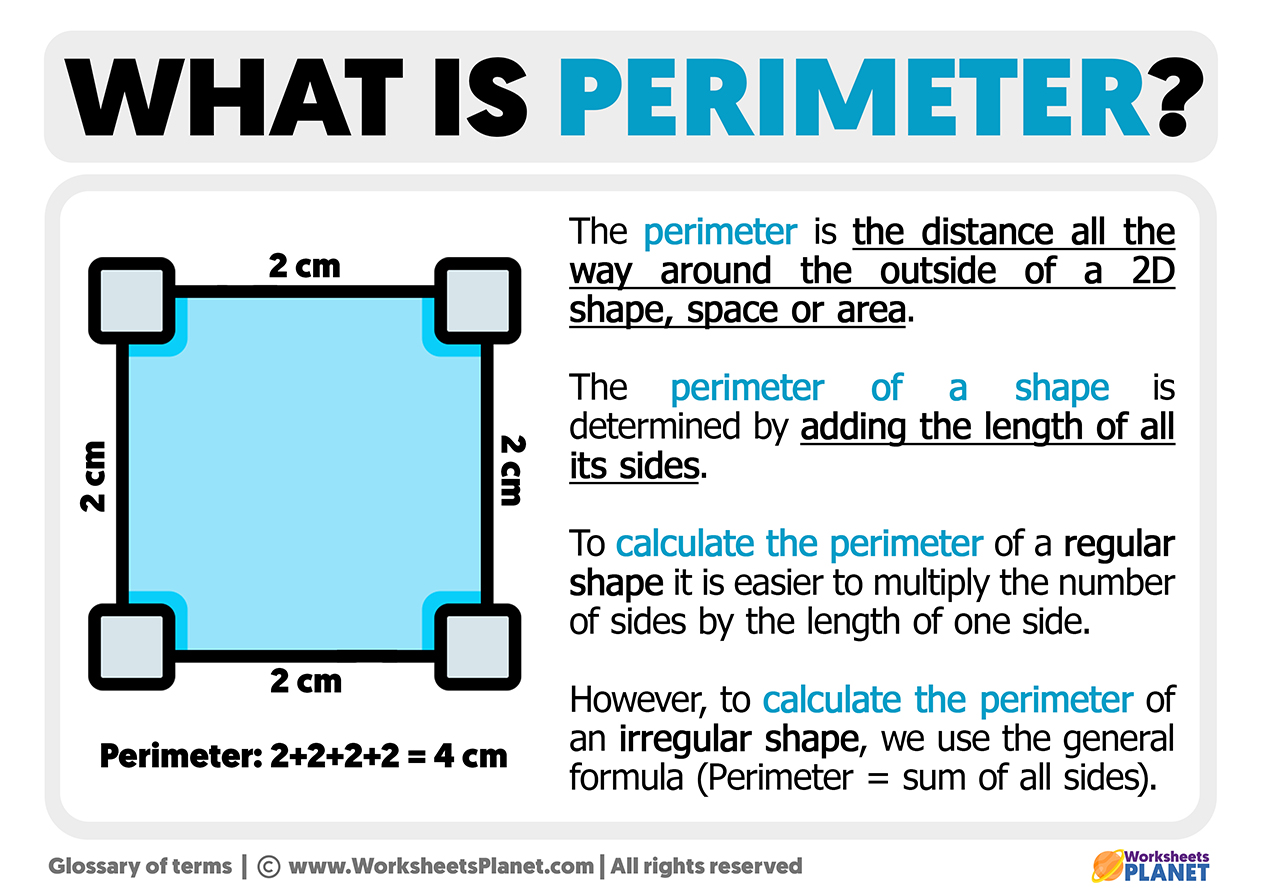
Perimeter of a Kite
The perimeter of a kite is the total distance around its edges. To calculate the perimeter, you can use the lengths of the kite's sides. A kite has two pairs of equal-length adjacent sides.
Formula
The basic formula to find the perimeter of a kite is:
Perimeter \( P = 2(a + b) \)
Where:
- \( a \) is the length of each side in one pair
- \( b \) is the length of each side in the other pair
Examples
Example 1: A kite has sides of lengths 12 cm and 10 cm. What is its perimeter?
Using the formula:
Perimeter \( P = 2(a + b) = 2(12 + 10) = 2 \times 22 = 44 \) cm
Example 2: Find the perimeter of a kite whose 2 adjacent sides are of lengths 9.3 cm and 17 cm.
Using the formula:
Perimeter \( P = 2(a + b) = 2(9.3 + 17) = 2 \times 26.3 = 52.6 \) cm
Perimeter Using Diagonals
In some cases, the perimeter of a kite can also be determined if the lengths of the diagonals are known, but typically the side lengths are used for simplicity.
Visual Representation
Below is a visual representation of a kite with its sides labeled:
Additional Resources
For further information on calculating the perimeter of a kite and other geometric properties, you can explore more detailed explanations and interactive tools on educational websites.

READ MORE:
Introduction
A kite is a fascinating geometric shape with distinct properties that set it apart from other quadrilaterals. Understanding the perimeter of a kite involves a simple yet interesting formula. A kite has two pairs of adjacent sides that are equal in length. To calculate its perimeter, you sum the lengths of these sides. This concept not only aids in geometric calculations but also finds applications in various real-world scenarios.
- Definition of a Kite
- Properties of a Kite
- Formula for Perimeter
- Example Calculation
The formula for the perimeter of a kite is given by:
\[
P = 2(a + b)
\]
where \(a\) and \(b\) are the lengths of the two pairs of equal sides. This formula is derived from the basic principle of adding the lengths of all sides of the kite.
Let's explore the concept with a practical example. Suppose a kite has sides of lengths 5 cm and 7 cm. Using the perimeter formula, we get:
\[
P = 2(5 + 7) = 2 \times 12 = 24 \, \text{cm}
\]
This step-by-step approach helps in reinforcing the understanding of geometric principles and their practical applications.
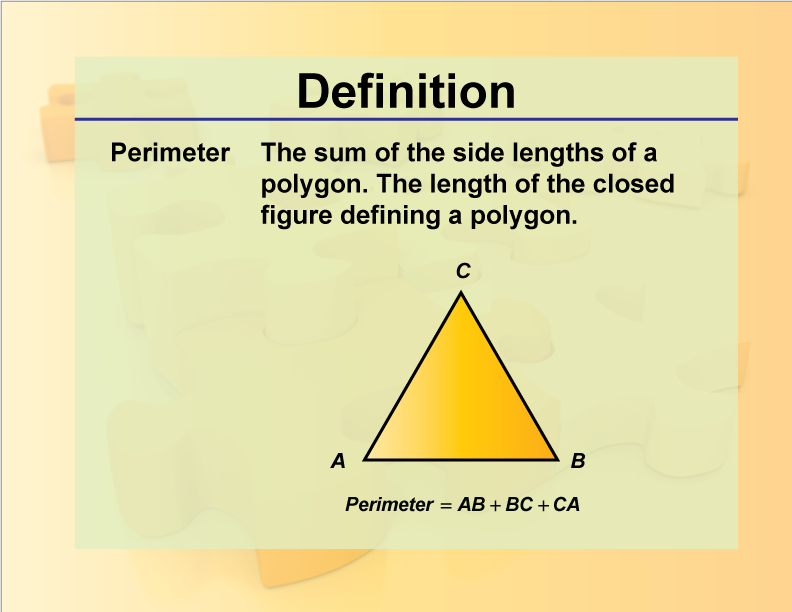
Definition of a Kite
A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent. This means that in a kite, two pairs of consecutive sides are of equal length. A kite is a special type of polygon that has unique properties and characteristics.
To understand the definition of a kite better, consider the following points:
- Two Pairs of Congruent Sides: In a kite, there are two pairs of adjacent sides that are equal in length. These pairs are distinct from each other.
- Diagonals: The diagonals of a kite intersect at right angles (90 degrees). One of the diagonals bisects the other.
- Angles: A kite has one pair of opposite angles that are equal. These are the angles between the pairs of congruent sides.
Here is a visual representation of a kite:

|
The main features of a kite can be summarized as follows:
- Adjacent Congruent Sides: Two pairs of sides next to each other are of equal length.
- Perpendicular Diagonals: The diagonals intersect at right angles.
- Symmetrical: The kite is symmetrical along the axis that bisects one of the diagonals.
Mathematically, a kite can be defined as follows:
- If \(AB = AD\) and \(BC = CD\), then quadrilateral ABCD is a kite.
- Let the diagonals intersect at point \(O\), then \(OA = OC\) and \(OB = OD\).
Properties of a Kite
A kite is a fascinating quadrilateral with several unique properties. Understanding these properties helps in recognizing kites and solving related geometric problems. Below are the key properties of a kite:
- Two Pairs of Adjacent Congruent Sides: A kite has two distinct pairs of adjacent sides that are equal in length. If we label the kite as ABCD, then AB = AD and BC = CD.
- One Pair of Opposite Angles are Congruent: The angles between the pairs of equal sides are congruent. For kite ABCD, ∠B = ∠D.
- Diagonals are Perpendicular: The diagonals of a kite intersect at right angles (90 degrees). If the diagonals are AC and BD, then they meet at right angles.
- One Diagonal Bisects the Other: One of the diagonals bisects the other diagonal at the point of their intersection. In kite ABCD, if AC and BD intersect at point O, then AO = CO and BO = DO.
- Symmetry: A kite is symmetric along the diagonal that bisects the angles between the pairs of congruent sides.
Here is a visual representation of the properties of a kite:

|
In addition to the above properties, consider the following mathematical characteristics:
- Perimeter: The perimeter of a kite can be calculated using the formula: \[ P = 2(a + b) \] where \(a\) and \(b\) are the lengths of the pairs of adjacent congruent sides.
- Area: The area of a kite can be determined using the lengths of its diagonals. If the diagonals are \(d_1\) and \(d_2\), then the area \(A\) is given by: \[ A = \frac{1}{2} d_1 d_2 \]
These properties make kites distinct and help in solving geometric problems involving kites efficiently.
Types of Kites
Kites, as geometric shapes, come in various types based on their properties and dimensions. Understanding these types helps in recognizing their unique characteristics and applications. Here are the main types of kites:
- Convex Kites: These are the most common types of kites where all interior angles are less than 180 degrees. The diagonals intersect at a right angle, and one diagonal bisects the other.
- Concave Kites: Also known as arrowhead kites, concave kites have one interior angle greater than 180 degrees. They still maintain the property of having two pairs of adjacent sides that are equal in length.
Here is a visual representation of the types of kites:

|

|
| Convex Kite | Concave Kite (Arrowhead) |
Convex and concave kites can further be classified based on their specific properties:
- Right Kite: A special type of convex kite where one pair of adjacent sides are perpendicular to each other, forming a right angle. This type is often used in tiling and various geometric constructions.
- Rhombic Kite: This is a kite where all four sides are of equal length, essentially making it a rhombus. It retains the properties of kites but with additional symmetries.
These classifications help in identifying and understanding the different forms kites can take in geometry and their respective properties.

Perimeter of a Kite
The perimeter of a kite is the total length around the shape, which can be calculated easily if the lengths of its sides are known. Since a kite has two pairs of adjacent sides that are equal in length, the formula for the perimeter is straightforward.
Let the lengths of the two pairs of adjacent sides be \(a\) and \(b\). Then the perimeter \(P\) of the kite can be calculated using the formula:
\[
P = 2(a + b)
\]
Here is a step-by-step method to find the perimeter of a kite:
- Identify the lengths of the sides: Measure the lengths of the two pairs of adjacent sides. Let these lengths be \(a\) and \(b\).
- Apply the perimeter formula: Use the formula \(P = 2(a + b)\) to calculate the perimeter.
- Calculate the result: Add the lengths of the sides and then multiply by 2 to get the perimeter.
For example, if the lengths of the sides of a kite are 5 cm and 7 cm, the perimeter can be calculated as follows:
- Let \(a = 5\) cm and \(b = 7\) cm.
- Apply the formula: \(P = 2(a + b) = 2(5 + 7) = 2 \times 12 = 24\) cm.
Therefore, the perimeter of the kite is 24 cm.
Here's a visual representation to help understand the calculation:

|
By following these steps, you can easily find the perimeter of any kite, provided you know the lengths of its sides.
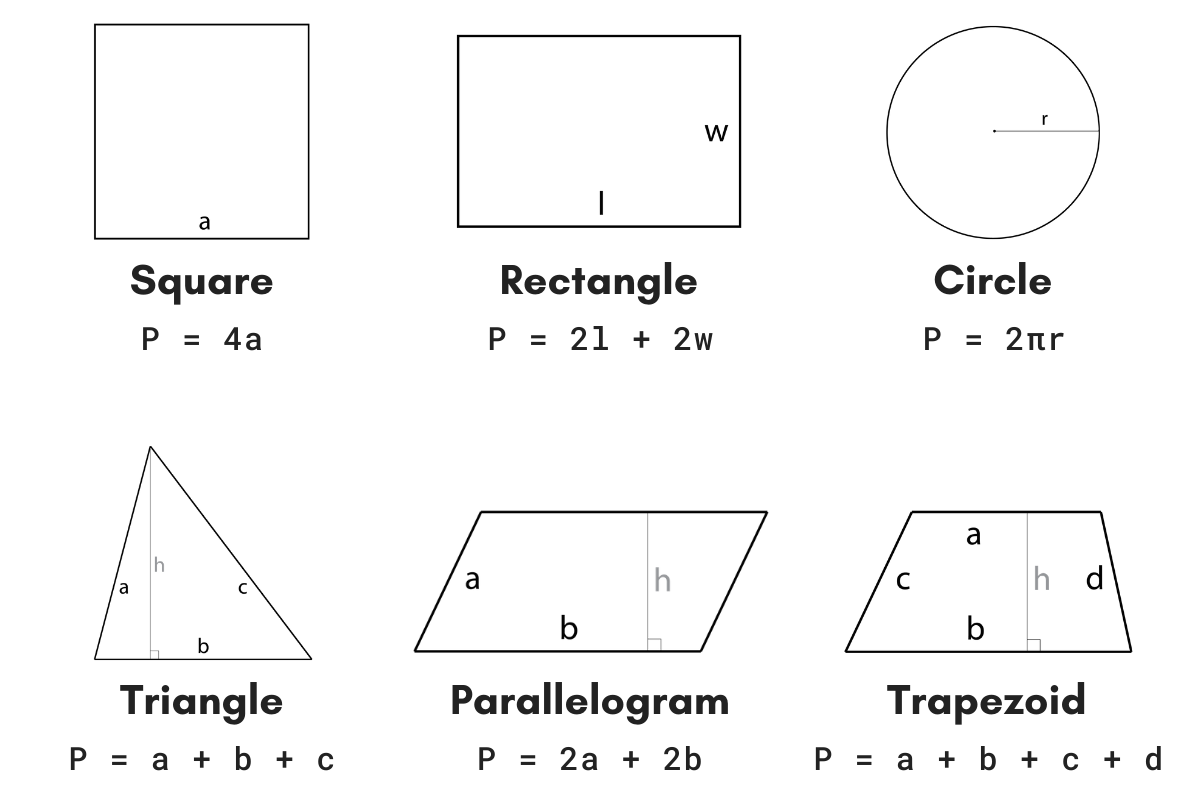
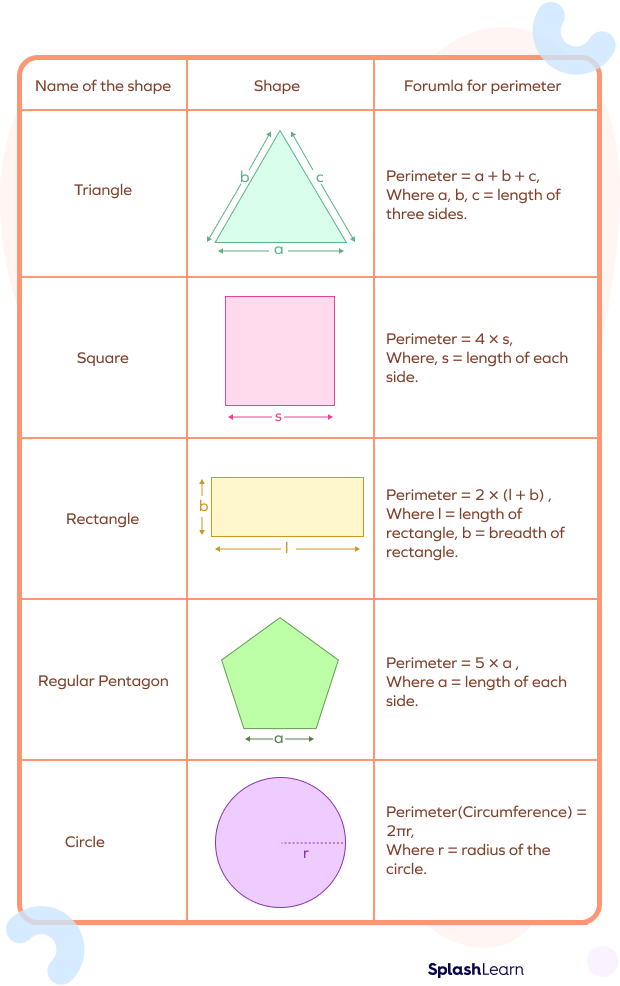
Formulas Related to Kites
Kites possess unique geometric properties that can be expressed through various mathematical formulas. These formulas help in calculating important aspects such as perimeter, area, and the lengths of the diagonals. Below are the essential formulas related to kites:
- Perimeter of a Kite: The perimeter (P) of a kite can be calculated using the lengths of its two pairs of adjacent sides, \(a\) and \(b\). \[ P = 2(a + b) \]
- Area of a Kite: The area (A) of a kite can be determined using the lengths of its diagonals, \(d_1\) and \(d_2\). \[ A = \frac{1}{2} d_1 d_2 \]
- Length of Diagonals: The lengths of the diagonals can be found if the area and one diagonal are known. For example, if the area (A) and one diagonal (\(d_1\)) are known, the length of the other diagonal (\(d_2\)) can be calculated as follows: \[ d_2 = \frac{2A}{d_1} \]
- Relation Between Sides and Angles: If the angles between the pairs of congruent sides are known, trigonometric formulas can be applied to find side lengths or other angles. For instance, if the angle between sides \(a\) and \(b\) is \(\theta\), the length of one of the diagonals can be expressed as: \[ d_1 = \sqrt{a^2 + b^2 + 2ab \cos(\theta)} \]
Below is a table summarizing these formulas:
| Formula | Description |
|---|---|
| \(P = 2(a + b)\) | Perimeter of the kite, where \(a\) and \(b\) are the lengths of adjacent sides. |
| \(A = \frac{1}{2} d_1 d_2\) | Area of the kite, where \(d_1\) and \(d_2\) are the lengths of the diagonals. |
| \(d_2 = \frac{2A}{d_1}\) | Length of the second diagonal, given the area and the length of the first diagonal. |
| \(d_1 = \sqrt{a^2 + b^2 + 2ab \cos(\theta)}\) | Length of a diagonal given the lengths of adjacent sides \(a\) and \(b\), and the angle \(\theta\) between them. |
These formulas are fundamental in solving various geometric problems involving kites and help in deriving other related properties and measures.
FAQs
Here are some frequently asked questions about kites, their properties, and related formulas:
1. What is a kite in geometry?
A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent. This means that each pair of adjacent sides are of equal length.
2. How do you calculate the perimeter of a kite?
The perimeter of a kite is calculated using the lengths of its two pairs of adjacent sides. If the lengths are \(a\) and \(b\), the formula for the perimeter \(P\) is:
\[
P = 2(a + b)
\]
3. What is the formula for the area of a kite?
The area of a kite can be calculated using the lengths of its diagonals \(d_1\) and \(d_2\). The formula for the area \(A\) is:
\[
A = \frac{1}{2} d_1 d_2
\]
4. How are the diagonals of a kite related?
The diagonals of a kite intersect at right angles (90 degrees). One of the diagonals bisects the other. This means that if the diagonals are \(d_1\) and \(d_2\), they form two right-angled triangles at the intersection point.
5. Can a kite be a rhombus?
Yes, a rhombus is a special type of kite where all four sides are of equal length. In this case, the rhombus retains all the properties of a kite, but with additional symmetries.
6. What is a concave kite?
A concave kite, also known as an arrowhead, has one interior angle greater than 180 degrees. It still has two pairs of adjacent sides that are equal in length, but the shape appears 'indented' or 'arrow-like' at one vertex.
7. How can you find the length of a diagonal in a kite?
If you know the area of the kite and the length of one diagonal, you can find the length of the other diagonal using the formula:
\[
d_2 = \frac{2A}{d_1}
\]
where \(A\) is the area and \(d_1\) is the length of the known diagonal.
8. Are the opposite angles in a kite equal?
In a kite, one pair of opposite angles are equal. These are the angles between the pairs of congruent sides.
9. What are the properties of the sides and angles of a kite?
- Two pairs of adjacent sides are equal in length.
- One pair of opposite angles are equal.
- The diagonals intersect at right angles, and one diagonal bisects the other.
These FAQs cover the fundamental aspects and properties of kites, helping to understand their geometric characteristics and related formulas.
Video hướng dẫn chi tiết cách tính diện tích và chu vi của một cánh diều, giúp bạn hiểu rõ các công thức liên quan.
Tìm Diện Tích và Chu Vi Của Một Cánh Diều: Hướng Dẫn Từng Bước
READ MORE:
Chu vi của Một Tam Giác, Hình Chữ Nhật, Cánh Cầu Vồng, Hình Thoi được Hình Thức Hóa
Chu vi của Một Tam Giác, Hình Chữ Nhật, Cánh Cầu Vồng, Hình Thoi được Hình Thức Hóa