Topic perimeter equals: Perimeter equals the total distance around the edges of any two-dimensional shape. From basic polygons like triangles and squares to circles and irregular shapes, understanding how to calculate perimeter is essential in geometry. This article explores formulas, examples, and practical applications to help you master perimeter calculations with ease.
Table of Content
- Perimeter Calculation
- Introduction to Perimeter
- Perimeter Formulas for Basic Shapes
- Perimeter Formulas for Polygons
- Perimeter of Complex Shapes
- Applications of Perimeter Calculation
- Perimeter in Advanced Geometry
- Historical Context and Mathematical Approximations
- Tools and Resources for Calculating Perimeters
- YOUTUBE: Xem video này để hiểu cách tính chu vi của các hình học cơ bản và phức tạp.
Perimeter Calculation
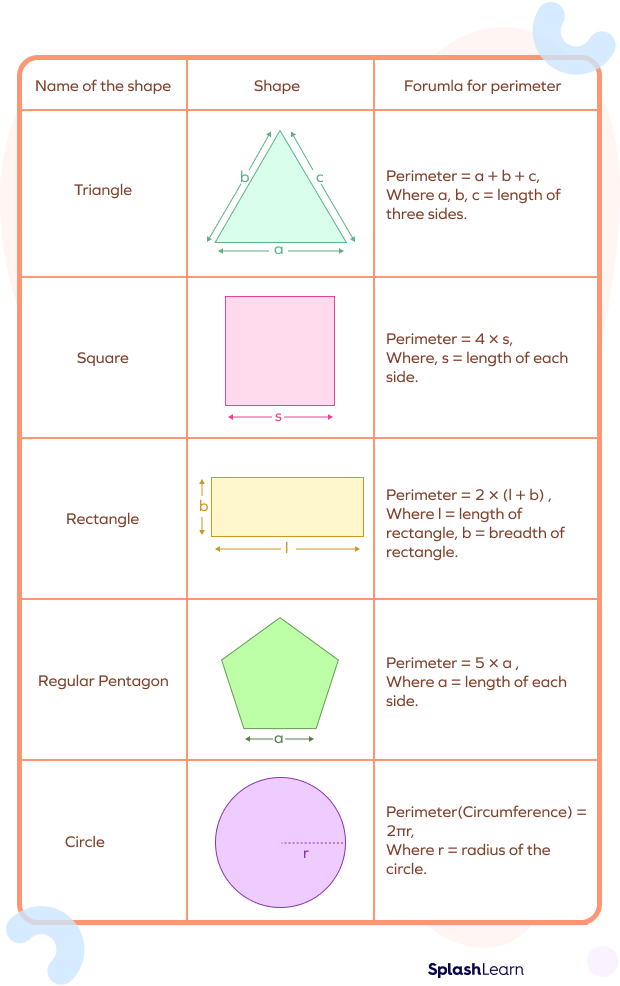
The perimeter of a shape is the total length of its boundary. It can be calculated using different formulas depending on the shape. Here are some common shapes and their perimeter formulas:
Perimeter Formulas
- Circle: \(P = 2 \pi r\)
- Triangle: \(P = a + b + c\)
- Square: \(P = 4a\)
- Rectangle: \(P = 2(l + w)\)
- Parallelogram: \(P = 2(a + b)\)
- Polygon: \(P = \sum_{i=1}^{n} a_i\)
Examples
-
Example 1: Circle
Given a circle with a radius of 7 cm:
Perimeter \(= 2 \pi \times 7 = 44 \, \text{cm}\)
-
Example 2: Rectangle
Given a rectangle with length 5 cm and width 3 cm:
Perimeter \(= 2(5 + 3) = 16 \, \text{cm}\)
-
Example 3: Equilateral Triangle
Given an equilateral triangle with side length 6 cm:
Perimeter \(= 3 \times 6 = 18 \, \text{cm}\)
Using Tools to Calculate Perimeter
There are various online tools available to help calculate the perimeter of different shapes accurately. These tools can simplify complex calculations and provide quick results.

READ MORE:
Introduction to Perimeter
The perimeter of a shape is the total length of its boundary. It is a fundamental concept in geometry and is used to measure the distance around various two-dimensional shapes. The perimeter is calculated by adding the lengths of all the sides of the shape. Different formulas are used for regular and irregular polygons to determine their perimeters.
- Regular Polygons: For regular polygons, where all sides are of equal length, the perimeter (P) can be calculated using the formula:
$$ P = n \times a $$
where \( n \) is the number of sides and \( a \) is the length of one side.
- Irregular Polygons: For irregular polygons, the perimeter is the sum of the lengths of all sides:
$$ P = a_1 + a_2 + a_3 + \ldots + a_n $$
where \( a_i \) represents the length of each side.
- Common Shapes:
- Square: \( P = 4a \) where \( a \) is the side length.
- Rectangle: \( P = 2(l + w) \) where \( l \) is the length and \( w \) is the width.
- Triangle: \( P = a + b + c \) where \( a, b, \) and \( c \) are the side lengths.
- Circle: Perimeter (Circumference) \( P = 2\pi r \) where \( r \) is the radius.
Understanding the concept of perimeter helps in solving various real-life problems such as fencing a garden, framing a picture, or any scenario involving the boundary of a shape.
Perimeter Formulas for Basic Shapes
The perimeter is the total distance around the edge of a two-dimensional shape. Here are the perimeter formulas for some basic geometric shapes:
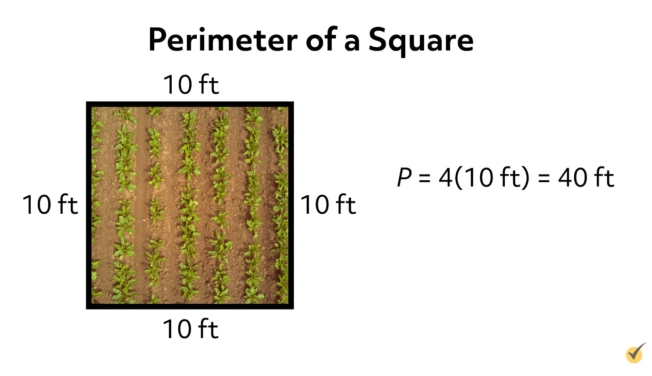
- Square: The perimeter of a square with side length \( s \) is: \[ P = 4s \]
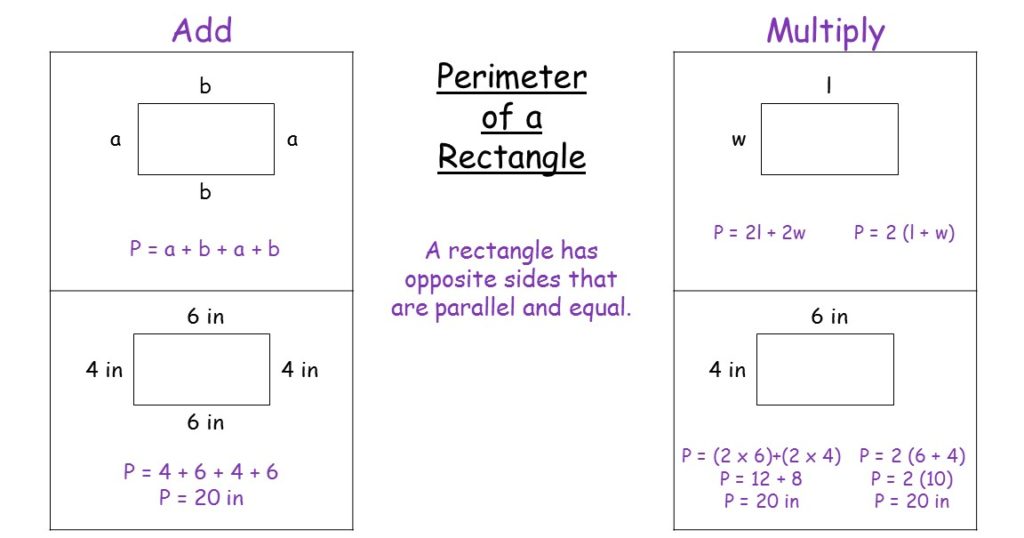
- Rectangle: The perimeter of a rectangle with length \( l \) and width \( w \) is: \[ P = 2l + 2w \]
- Triangle: The perimeter of a triangle with sides \( a \), \( b \), and \( c \) is: \[ P = a + b + c \]
- Circle (Circumference): The perimeter of a circle with radius \( r \) is: \[ C = 2\pi r \]
- Regular Polygon: The perimeter of a regular polygon with \( n \) sides, each of length \( s \), is: \[ P = ns \]
- Parallelogram: The perimeter of a parallelogram with sides \( a \) and \( b \) is: \[ P = 2(a + b) \]
- Trapezoid: The perimeter of a trapezoid with sides \( a \), \( b \), \( c \), and \( d \) is: \[ P = a + b + c + d \]
Using these formulas, you can calculate the perimeter of most basic shapes by simply knowing the lengths of their sides or radii.
Perimeter Formulas for Polygons
The perimeter of a polygon is the total distance around the outer sides of the shape. For regular polygons (where all sides and angles are equal), and irregular polygons (where sides and angles are not necessarily equal), there are specific formulas to calculate the perimeter.
| Shape | Formula | Example Calculation |
|---|---|---|
| Triangle | \( P = a + b + c \) | If \( a = 3 \, \text{cm}, b = 4 \, \text{cm}, c = 5 \, \text{cm} \), then \( P = 3 + 4 + 5 = 12 \, \text{cm} \) |
| Square | \( P = 4s \) | If \( s = 5 \, \text{cm} \), then \( P = 4 \times 5 = 20 \, \text{cm} \) |
| Rectangle | \( P = 2(l + w) \) | If \( l = 6 \, \text{cm} \) and \( w = 4 \, \text{cm} \), then \( P = 2(6 + 4) = 20 \, \text{cm} \) |
| Pentagon | \( P = 5s \) | If \( s = 3 \, \text{cm} \), then \( P = 5 \times 3 = 15 \, \text{cm} \) |
| Regular n-sided Polygon | \( P = ns \) | If \( n = 6 \) and \( s = 4 \, \text{cm} \), then \( P = 6 \times 4 = 24 \, \text{cm} \) |
| Irregular Polygon | \( P = a_1 + a_2 + \cdots + a_n \) | If the sides are \( 2 \, \text{cm}, 3 \, \text{cm}, 4 \, \text{cm}, \) and \( 5 \, \text{cm} \), then \( P = 2 + 3 + 4 + 5 = 14 \, \text{cm} \) |
To summarize, the perimeter of any polygon can be found by adding the lengths of all its sides. For regular polygons, you can use a simpler multiplication formula based on the number of sides and the length of one side.
Perimeter of Complex Shapes
Calculating the perimeter of complex shapes involves adding the lengths of all sides. For irregular shapes, this process can be broken down into simpler steps by dividing the shape into familiar geometric figures like rectangles, squares, and triangles.
Example 1: Perimeter of a Complex Shape
Consider a shape composed of a rectangle and a square:
- The rectangle has a width of 7 km and a height of 2 km.
- The square has sides of 5 km each.
To find the perimeter, sum the lengths of all sides:
Perimeter = 7 km + 2 km + 7 km + 2 km + 5 km + 5 km = 28 km
Example 2: Perimeter of a Combined Shape
Consider a shape that can be divided into two rectangles:
- Rectangle 1: 8 m by 9 m
- Rectangle 2: 6 m by 16 m
Calculate the perimeter by summing the sides:
- Rectangle 1: Perimeter = 2(8 m + 9 m) = 34 m
- Rectangle 2: Perimeter = 2(6 m + 16 m) = 44 m
Since the rectangles share a common side, subtract the shared side from the total:
Total Perimeter = 34 m + 44 m - 16 m = 62 m
Example 3: Irregular Polygon
For an irregular polygon, sum the lengths of all its sides. For instance, a polygon with side lengths of 6 cm, 5 cm, 5 cm, 4 cm, and 3 cm would have:
Perimeter = 6 cm + 5 cm + 5 cm + 4 cm + 3 cm = 23 cm
Steps to Calculate Perimeter of Complex Shapes
- Identify and label the sides of the shape.
- Break down the complex shape into simpler geometric figures if possible.
- Calculate the perimeter of each simple shape.
- Add the perimeters of all simple shapes, adjusting for any shared sides or overlapping areas.
Tools and Tips
Using graph paper or geometry software can help visualize and accurately measure complex shapes. Online calculators and math learning websites often provide interactive tools to practice these calculations.
Applications of Perimeter Calculation
The concept of perimeter is widely used in various real-life applications. Here are some of the key areas where perimeter calculations are essential:
- Real-life Examples
Gardening and Landscaping: When planning a garden or landscaping project, knowing the perimeter helps in determining the amount of fencing, edging materials, or boundary markers required. For example, to enclose a rectangular garden, the perimeter is calculated as \( P = 2(l + w) \), where \( l \) is the length and \( w \) is the width.
Home Improvement: Perimeter calculations are used to measure the borders of rooms for installing baseboards, wallpaper, or painting. For a square room, the perimeter is \( P = 4s \), where \( s \) is the length of one side.
Sports Fields: The perimeter is crucial for designing and maintaining sports fields and tracks. For example, a rectangular football field's perimeter is \( P = 2(l + w) \).
- Practical Problems
Construction and Architecture: Perimeter calculations help in determining the materials needed for building structures. For instance, the perimeter of a rectangular plot is used to calculate the length of the fence required.
Urban Planning: City planners use perimeter calculations for designing roads, parks, and property boundaries. The perimeter of a block or lot is essential for zoning and planning purposes.
- Games and Exercises
Educational Tools: Perimeter problems are used in educational games and exercises to teach students geometry and spatial awareness. Calculating the perimeter of various shapes helps students understand the concept of measurement.
Fitness and Recreation: In fitness routines, tracking the perimeter of running tracks or walking paths helps in measuring distances covered. For example, the perimeter of a circular track is its circumference, \( C = 2\pi r \), where \( r \) is the radius.
Understanding the applications of perimeter calculation can significantly enhance problem-solving skills and practical knowledge in various fields.
Perimeter in Advanced Geometry
In advanced geometry, the concept of perimeter extends beyond simple shapes to more complex figures and higher-dimensional objects. Here are some key topics within this area:
-
Perimeter in Higher Dimensions
When dealing with higher dimensions, the perimeter often refers to the boundary length of shapes in higher-dimensional spaces. For instance, in three dimensions, the perimeter of a shape might be referred to as its surface perimeter.
- Example: The perimeter of a cube is the sum of the lengths of its edges, which can be calculated as \( 12 \times \text{side length} \).
-
Perimeter of Hypersurfaces
Hypersurfaces are generalizations of surfaces to higher dimensions. Calculating their perimeter involves understanding complex integrals over these surfaces.
- Example: The "perimeter" of a hypersphere (often called its surface area) in four dimensions is given by \( 2 \pi^2 r^3 \), where \( r \) is the radius.
-
Caccioppoli Sets
Caccioppoli sets, or sets of finite perimeter, are used in geometric measure theory to study shapes whose perimeter can be defined even if the shape is irregular or fractal-like.
- Example: For a set \( E \) in \( \mathbb{R}^n \), the perimeter can be defined using the concept of the measure of the boundary of \( E \).
Key Formulas and Concepts
Here are some important formulas and concepts related to advanced perimeter calculations:
- Surface Perimeter in 3D: For a polyhedron, the surface perimeter is the sum of the perimeters of its faces.
- Integral Formulas: In higher dimensions, perimeter calculations often involve integrals. For example, the perimeter (or length) of a curve in space can be found using: \[ \text{Perimeter} = \int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} \, dt \]
- Fractals: For fractal shapes, the perimeter may be infinite or depend on the scale at which it is measured, often requiring the use of fractal dimension in calculations.
Advanced geometry provides tools and frameworks for understanding and calculating the perimeter in complex scenarios, significantly extending the concept beyond simple shapes.
Historical Context and Mathematical Approximations
The concept of perimeter has been explored throughout history, leading to the development of various mathematical approximations and techniques. One of the earliest known instances of perimeter calculation is related to the approximation of pi (π), a fundamental constant in geometry.
-
Ancient Approximations
In ancient Babylon, around 1900–1680 BC, the value of π was approximated to be 3.125, while the Rhind Papyrus from ancient Egypt (ca. 1650 BC) indicates a value of 3.1605. These early attempts laid the foundation for more precise calculations in the future.
-
Archimedes' Method
Archimedes of Syracuse (287–212 BC) made a significant advancement by using inscribed and circumscribed polygons to approximate π. He demonstrated that the value of π lies between 3 1/7 (approximately 3.142857) and 3 10/71 (approximately 3.140845). Archimedes’ method involved iteratively doubling the number of polygon sides to narrow down the range.
His formulas for calculating the semi-perimeters of polygons are given by:
- For the inscribed polygon: \( b_k = 3 \cdot 2^k \sin(\theta_k) \)
- For the circumscribed polygon: \( a_k = 3 \cdot 2^k \tan(\theta_k) \)
Where \( \theta_k = 60^\circ / 2^k \).
-
Chinese Contributions
Zu Chongzhi (429–501 AD), an eminent Chinese mathematician, independently approximated π to be 355/113, a remarkably accurate value for his time. He likely used a method similar to Archimedes, involving inscribed polygons with up to 24,576 sides.
-
Development of Modern Notation
The Greek letter π was first introduced by Welsh mathematician William Jones in 1706 and later popularized by Leonhard Euler in 1737. This notation has since become a standard in mathematics.
-
Buffon's Needle Experiment
In the 18th century, Georges-Louis Leclerc, Comte de Buffon, devised a probabilistic method to estimate π, known as Buffon's Needle. This experiment involves dropping a needle on a lined surface and using the probability of the needle crossing a line to calculate π.
-
Advancements in the 18th and 19th Centuries
Over the centuries, mathematicians continued to improve the precision of π. In 1701, John Machin developed a formula allowing π to be calculated to 100 decimal places. Subsequent mathematicians, including Vega and Rutherford, extended this precision to over 400 decimal places by the mid-19th century.
-
Transcendence of π
In 1882, Ferdinand von Lindemann proved that π is transcendental, meaning it is not the root of any non-zero polynomial equation with rational coefficients. This discovery confirmed that it is impossible to square the circle using only a finite number of steps with compass and straightedge.
Tools and Resources for Calculating Perimeters
- Online Perimeter Calculators: Numerous websites offer free tools where you can input the dimensions of a shape, and they'll instantly calculate its perimeter. These calculators are convenient for quick computations and are often accompanied by explanations or formulas.
- Worksheets and Practice Problems: Educational platforms and math websites provide downloadable worksheets and practice problems specifically focused on perimeter calculations. These resources range from simple exercises for beginners to complex challenges for advanced learners, catering to various skill levels.
- Educational Games: Interactive games and apps designed for learning perimeter make the subject engaging and enjoyable for students of all ages. These games often incorporate puzzles, quizzes, and interactive activities to reinforce understanding and improve retention of perimeter concepts.

Xem video này để hiểu cách tính chu vi của các hình học cơ bản và phức tạp.
Video hướng dẫn "Toán Antics - Chu vi"
READ MORE:
Xem video này để tìm hiểu cách tính diện tích và chu vi của hình chữ nhật một cách dễ dàng và hiệu quả.
Cách tính Diện tích và Chu vi của Hình Chữ Nhật