Topic ellipse perimeter: Discover the fascinating world of ellipse perimeter calculations. This article delves into the mathematical intricacies, approximation methods, and practical applications. Whether you're a math enthusiast or a student, you'll gain a comprehensive understanding of how to determine the perimeter of an ellipse using various formulas and techniques.
Table of Content
- Ellipse Perimeter
- Introduction to Ellipse Perimeter
- Mathematical Definition of an Ellipse
- Formula for the Perimeter of an Ellipse
- Ramanujan's Approximation for Ellipse Perimeter
- Hudson's Approximation for Ellipse Perimeter
- Series Expansion for Ellipse Perimeter
- Complete Elliptic Integral Method
- Numerical Methods for Calculating Ellipse Perimeter
- Applications of Ellipse Perimeter Calculations
- Practical Examples
- YOUTUBE:
Ellipse Perimeter
The perimeter (or circumference) of an ellipse is more complex to calculate than that of a circle. There is no simple formula involving elementary functions to compute the exact perimeter of an ellipse. However, there are several approximations and series expansions that are commonly used.
Approximation Formulas
Here are some commonly used approximations for the perimeter \( P \) of an ellipse with semi-major axis \( a \) and semi-minor axis \( b \):
- Ramanujan's Approximation (1st Formula)
\[ P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \] - Ramanujan's Approximation (2nd Formula)
\[ P \approx \pi \left[ a + b \right] \left[ 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right] \]
where \( h = \frac{(a - b)^2}{(a + b)^2} \) - Hudson's Approximation
\[ P \approx \pi \left[ 1.5(a + b) - \sqrt{ab} \right] \]
Series Expansion
The exact perimeter of an ellipse can be expressed as an infinite series:
\[ P = 2\pi a \left[ 1 - \left( \frac{1}{4} \right) e^2 - \left( \frac{1}{64} \right) e^4 - \left( \frac{1}{256} \right) e^6 - \cdots \right] \]
where \( e \) is the eccentricity of the ellipse given by \( e = \sqrt{1 - \frac{b^2}{a^2}} \).
Elliptic Integrals
The perimeter can also be exactly calculated using elliptic integrals:
\[ P = 4a E(e) \]
where \( E(e) \) is the complete elliptic integral of the second kind.
Numerical Methods
For practical purposes, numerical methods can be used to compute the perimeter of an ellipse to a high degree of accuracy. These methods are particularly useful when dealing with ellipses where \( a \) and \( b \) differ significantly.
Conclusion
While there is no simple exact formula for the perimeter of an ellipse, various approximations and numerical methods provide accurate results. For most applications, Ramanujan's approximations are sufficiently precise and easy to use.

READ MORE:
Introduction to Ellipse Perimeter
The perimeter of an ellipse is a fundamental concept in geometry, describing the total distance around the ellipse. Unlike a circle, where the perimeter (or circumference) is straightforward to calculate, an ellipse presents a more complex challenge due to its elongated shape. The formula for calculating the perimeter of an ellipse does not have a simple closed-form solution involving elementary functions. Instead, various approximation methods and series expansions are used.
An ellipse is defined by two principal axes: the semi-major axis \( a \) and the semi-minor axis \( b \). These axes are perpendicular to each other and intersect at the ellipse's center. The complexity of calculating the perimeter arises from the continuous change in curvature along the ellipse.
Here are the key aspects of ellipse perimeter calculation:
- Exact Formulas: Involving elliptic integrals, which provide precise values but are complex to compute.
- Approximation Methods: Such as those developed by mathematicians like Ramanujan and Hudson, offering simpler yet highly accurate formulas.
- Numerical Methods: Using iterative techniques and computer algorithms to achieve high precision in practical applications.
Understanding the perimeter of an ellipse is not only a theoretical exercise but also has practical implications in fields such as astronomy, engineering, and physics, where elliptical shapes frequently occur.
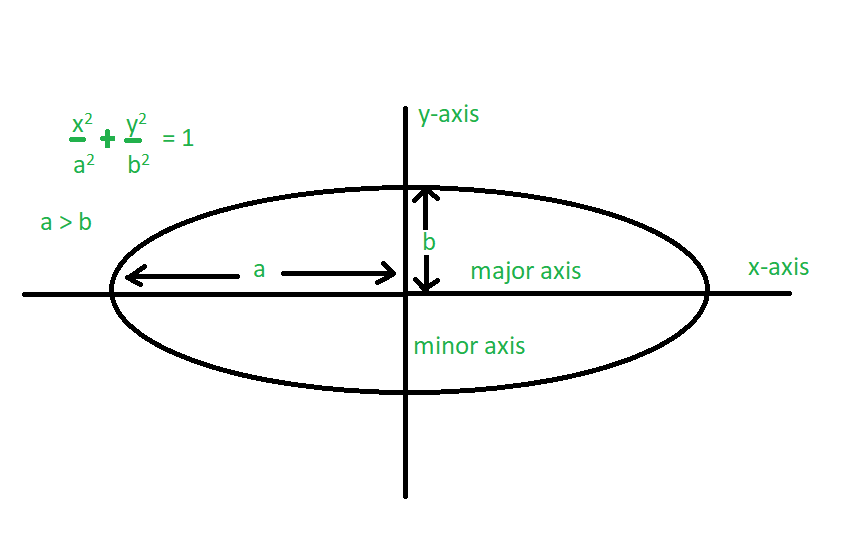
Mathematical Definition of an Ellipse
An ellipse is a geometric shape that appears as a flattened circle. It is defined as the set of all points in a plane where the sum of the distances from two fixed points (known as the foci) is constant. This unique property distinguishes ellipses from other conic sections.
The standard equation of an ellipse in Cartesian coordinates is given by:
\[
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
\]
where:
- \( a \) is the length of the semi-major axis (the longest radius).
- \( b \) is the length of the semi-minor axis (the shortest radius).
The foci of the ellipse are located along the major axis, at a distance of \( c \) from the center, where \( c \) is defined by the relationship:
\[
c = \sqrt{a^2 - b^2}
\]
The eccentricity \( e \) of the ellipse, a measure of its deviation from being a circle, is given by:
\[
e = \frac{c}{a} = \sqrt{1 - \frac{b^2}{a^2}}
\]
Important properties of an ellipse include:
- Axes: The major and minor axes intersect at the center of the ellipse, which is also the midpoint of the segment joining the foci.
- Vertices: The points where the ellipse intersects its major axis are called the vertices, located at \( (\pm a, 0) \).
- Co-vertices: The points where the ellipse intersects its minor axis, located at \( (0, \pm b) \).
An ellipse can also be described parametrically using the equations:
\[
x = a \cos(t) \quad \text{and} \quad y = b \sin(t)
\]
where \( t \) is a parameter that varies from 0 to \( 2\pi \).
These properties and equations provide a comprehensive understanding of the mathematical structure of an ellipse, allowing for various methods to analyze and calculate its perimeter.
Formula for the Perimeter of an Ellipse
The perimeter of an ellipse is more complex to calculate than the circumference of a circle. There is no simple closed-form formula involving elementary functions for the exact perimeter of an ellipse. However, several approximations and series expansions are used to estimate the perimeter accurately.
Let's start with the general form of the perimeter \( P \) for an ellipse with semi-major axis \( a \) and semi-minor axis \( b \). One of the common formulas used is based on the elliptic integral:
\[
P = 4a E(e)
\]
where:
- \( E(e) \) is the complete elliptic integral of the second kind.
- \( e \) is the eccentricity of the ellipse, given by \( e = \sqrt{1 - \frac{b^2}{a^2}} \).
Calculating the complete elliptic integral \( E(e) \) directly can be complicated, so various approximations are commonly used. Here are a few notable approximations:
- Ramanujan's Approximation (1st Formula):
\[
P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]
\] - Ramanujan's Approximation (2nd Formula):
\[
P \approx \pi \left( a + b \right) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right)
\]
where \( h = \frac{(a - b)^2}{(a + b)^2} \). - Hudson's Approximation:
\[
P \approx \pi \left[ 1.5(a + b) - \sqrt{ab} \right]
\]
For those who prefer a series expansion, the exact perimeter can be expressed as an infinite series:
\[
P = 2\pi a \left[ 1 - \left( \frac{1}{4} \right) e^2 - \left( \frac{1}{64} \right) e^4 - \left( \frac{1}{256} \right) e^6 - \cdots \right]
\]
Here, each successive term in the series provides a more accurate approximation of the ellipse's perimeter. The eccentricity \( e \) plays a significant role in these calculations, influencing the accuracy and convergence of the series.
Overall, while there is no simple exact formula for the perimeter of an ellipse, the approximations and series expansions provide effective methods for obtaining accurate results. These methods are essential for applications in various scientific and engineering fields where precise measurements of elliptical shapes are required.
Ramanujan's Approximation for Ellipse Perimeter
Srinivasa Ramanujan, a renowned mathematician, developed several approximations for calculating the perimeter of an ellipse. These approximations are widely appreciated for their simplicity and accuracy. Here, we explore two of Ramanujan's most famous formulas for approximating the perimeter of an ellipse with semi-major axis \( a \) and semi-minor axis \( b \).
First Approximation
Ramanujan's first approximation for the perimeter \( P \) of an ellipse is given by the formula:
\[
P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]
\]
This formula provides a good approximation and is relatively easy to use, involving only basic arithmetic operations and a square root.
Second Approximation
Ramanujan's second approximation is slightly more complex but offers an even higher degree of accuracy. It is expressed as:
\[
P \approx \pi (a + b) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right)
\]
where:
\[
h = \frac{(a - b)^2}{(a + b)^2}
\]
In this formula, \( h \) represents the squared difference of the axes divided by their squared sum. This approximation is particularly useful when the difference between \( a \) and \( b \) is significant.
To summarize the steps involved in using Ramanujan's second approximation:
- Calculate \( h \):
\[
h = \frac{(a - b)^2}{(a + b)^2}
\] - Substitute \( h \) into the formula:
\[
P \approx \pi (a + b) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right)
\]
Both of these approximations provide highly accurate results and are useful tools for mathematicians, engineers, and scientists working with elliptical shapes. Ramanujan's contributions continue to be valuable in the field of mathematical approximations.
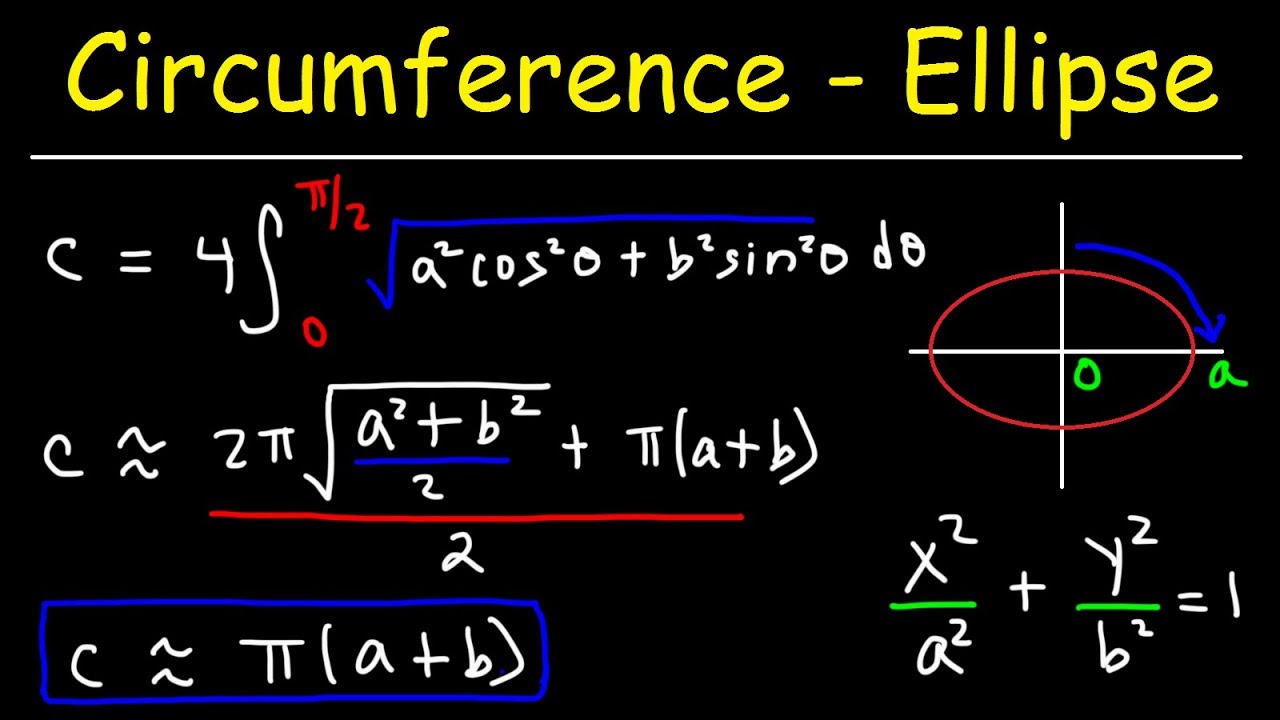
Hudson's Approximation for Ellipse Perimeter
Hudson's approximation provides a simple yet effective method for estimating the perimeter of an ellipse. This approximation is particularly useful for its straightforwardness and ease of calculation. For an ellipse with semi-major axis \( a \) and semi-minor axis \( b \), Hudson's approximation is given by:
\[
P \approx \pi \left[ 1.5(a + b) - \sqrt{ab} \right]
\]
This formula balances simplicity with accuracy, making it a convenient choice for quick calculations. Here are the steps to use Hudson's approximation:
- Calculate the sum of the semi-major and semi-minor axes:
\[
S = a + b
\] - Calculate the product of the semi-major and semi-minor axes:
\[
P = ab
\] - Apply Hudson's formula:
\[
P \approx \pi \left[ 1.5S - \sqrt{P} \right]
\]
This approximation, while not as precise as Ramanujan's, offers a quick and reasonably accurate method to estimate the perimeter, especially when an approximate value suffices.
Hudson's approximation simplifies the complex nature of elliptical perimeter calculations, providing an accessible tool for various practical applications in science and engineering.
Series Expansion for Ellipse Perimeter
Calculating the exact perimeter of an ellipse can be approached using a series expansion. This method provides a way to express the perimeter as an infinite series, converging to the exact value. The series expansion involves the eccentricity of the ellipse and offers high precision for practical computations.
The general form of the series expansion for the perimeter \( P \) of an ellipse with semi-major axis \( a \) and semi-minor axis \( b \) is given by:
\[
P = 2\pi a \left[ 1 - \left( \frac{1}{4} \right) e^2 - \left( \frac{1}{64} \right) e^4 - \left( \frac{1}{256} \right) e^6 - \cdots \right]
\]
where \( e \) is the eccentricity of the ellipse, defined as:
\[
e = \sqrt{1 - \frac{b^2}{a^2}}
\]
To utilize this series expansion, follow these steps:
- Calculate the eccentricity \( e \):
\[
e = \sqrt{1 - \frac{b^2}{a^2}}
\] - Substitute \( e \) into the series expansion formula:
\[
P = 2\pi a \left[ 1 - \left( \frac{1}{4} \right) e^2 - \left( \frac{1}{64} \right) e^4 - \left( \frac{1}{256} \right) e^6 - \cdots \right]
\]
Each term in the series provides a more accurate approximation of the ellipse's perimeter. The series converges rapidly for ellipses with low eccentricity (i.e., shapes closer to a circle).
In practice, truncating the series after a few terms often yields a sufficiently accurate approximation for most applications. For example, considering the first three terms gives:
\[
P \approx 2\pi a \left[ 1 - \left( \frac{1}{4} \right) e^2 - \left( \frac{1}{64} \right) e^4 \right]
\]
This approach provides a balance between computational simplicity and precision, making it useful for various scientific and engineering applications where the exact perimeter of an ellipse is required.
Complete Elliptic Integral Method
The perimeter of an ellipse can be accurately calculated using the complete elliptic integral of the second kind. This method is derived from the integral calculus and provides a precise value for the ellipse perimeter, especially when the ellipse's eccentricity is not too close to 1.
The complete elliptic integral of the second kind, \( E \), is given by the integral:
\[ E(k) = \int_0^{\pi/2} \sqrt{1 - k^2 \sin^2 \theta} \, d\theta \]
For an ellipse with semi-major axis \( a \) and semi-minor axis \( b \), the eccentricity \( e \) is defined as:
\[ e = \sqrt{1 - \frac{b^2}{a^2}} \]
The parameter \( k \) in the elliptic integral is the eccentricity \( e \) of the ellipse.
The formula for the perimeter \( P \) of the ellipse using the complete elliptic integral of the second kind is:
\[ P \approx 4aE(e) \]
Where \( E(e) \) is the complete elliptic integral of the second kind evaluated at \( e \).
To calculate the perimeter using this method, follow these steps:
- Determine the semi-major axis \( a \) and semi-minor axis \( b \) of the ellipse.
- Calculate the eccentricity \( e \) using the formula:
\[ e = \sqrt{1 - \frac{b^2}{a^2}} \] - Evaluate the complete elliptic integral of the second kind, \( E(e) \), for the calculated eccentricity.
- Multiply \( 4a \) by \( E(e) \) to get the perimeter \( P \) of the ellipse:
\[ P \approx 4aE(e) \]
This method is precise and widely used in mathematical calculations involving ellipses. The complete elliptic integral can be computed using numerical methods or approximations available in many mathematical software packages.
Numerical Methods for Calculating Ellipse Perimeter
Calculating the exact perimeter of an ellipse involves complex integrals that generally cannot be solved in closed form. However, numerical methods provide effective ways to approximate the perimeter with high precision. Here, we outline some of the key numerical methods used for this purpose.
1. Approximation Formulas
- Ramanujan's Approximation: One of the most famous approximations by Srinivasa Ramanujan is given by: \[ P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \] where \(a\) is the semi-major axis and \(b\) is the semi-minor axis of the ellipse.
- Hudson's Approximation: Another useful approximation is provided by Hudson: \[ P \approx \pi \left[ (a + b) \left( 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right) \right] \] where \(h = \left( \frac{a - b}{a + b} \right)^2\).
2. Series Expansion
The perimeter can be approximated using a series expansion involving the eccentricity \(e\). The series is:
\[
P = 2\pi a \left[ 1 - \left( \frac{1}{2} \right)^2 e^2 - \left( \frac{1 \cdot 3}{2 \cdot 4} \right)^2 \frac{e^4}{3} - \cdots \right]
\]
where \(e = \sqrt{1 - \frac{b^2}{a^2}}\) is the eccentricity of the ellipse.
3. Numerical Integration
The perimeter can be numerically integrated using the following integral:
\[
P = 4a \int_0^{\frac{\pi}{2}} \sqrt{1 - e^2 \sin^2 \theta} \, d\theta
\]
Since this integral does not have a closed-form solution, numerical methods like Simpson's Rule or Gaussian Quadrature can be used to evaluate it.
Simpson's Rule Example:
- Divide the interval \([0, \frac{\pi}{2}]\) into \(n\) equal parts.
- Calculate the function values at each division point.
- Apply Simpson's Rule to approximate the integral: \[ \int_0^{\frac{\pi}{2}} \sqrt{1 - e^2 \sin^2 \theta} \, d\theta \approx \frac{\pi}{2n} \left[ f(0) + 4 \sum_{i=1,3,5,\ldots}^{n-1} f(\theta_i) + 2 \sum_{i=2,4,6,\ldots}^{n-2} f(\theta_i) + f\left(\frac{\pi}{2}\right) \right] \]
4. Computational Tools
Various online calculators and software tools can perform these numerical integrations with ease. For example, entering the semi-major and semi-minor axis lengths into an ellipse perimeter calculator can yield quick and accurate results.
Conclusion
While exact calculation of an ellipse's perimeter is complex, these numerical methods and approximations provide practical means to obtain precise results. Whether through approximation formulas, series expansions, or numerical integration, these methods make the task manageable.
Applications of Ellipse Perimeter Calculations
Calculating the perimeter of an ellipse has a variety of applications across different fields. Below are some key areas where these calculations are particularly useful:
- Engineering and Architecture
In engineering and architecture, ellipses are often used in the design of structures such as arches, bridges, tunnels, and domes. Calculating the perimeter helps in determining the amount of material needed, ensuring structural integrity and cost-efficiency. For example, the length of the fence around an elliptical garden or the framing needed for an elliptical window can be determined using the ellipse perimeter.
- Astronomy
Ellipses play a crucial role in astronomy, particularly in the study of planetary orbits. The orbits of planets and other celestial bodies are often elliptical in shape. By calculating the perimeter, astronomers can determine the distance a planet travels in its orbit, which is essential for understanding orbital dynamics and predicting celestial events like eclipses and alignments.
- Sports
In the design of running tracks, the curved portions are typically elliptical to allow athletes to maintain speed while turning. Calculating the perimeter ensures that the track meets regulatory standards and provides a fair and safe surface for competitions.
- Automotive Engineering
The motion of pistons within an engine can be approximated using elliptical shapes. Calculating the perimeter helps in optimizing the size and shape of pistons, which in turn improves the engine's efficiency and performance.
- Medical Prosthetics
In the design of prosthetic limbs, elliptical shapes are often used to match the natural contours of the human body. Calculating the perimeter ensures a snug fit, enhancing comfort and functionality for the user.
- Jewelry Design
Elliptical shapes are popular in jewelry design for items like rings, bracelets, and necklaces. Calculating the perimeter is important for ensuring that the pieces fit well and are comfortable to wear.
Overall, the ability to calculate the perimeter of an ellipse is a valuable tool in various scientific, engineering, and design applications, helping professionals create more efficient, effective, and aesthetically pleasing results.
Practical Examples
Ellipses appear in various real-world applications, showcasing their importance in multiple fields. Here are some practical examples where the calculation of the perimeter of an ellipse is essential:
- Astronomy:
The orbits of planets and satellites are elliptical. Accurate calculations of these elliptical paths are crucial for understanding celestial mechanics and planning space missions.
- Engineering:
In engineering, elliptical shapes are used in the design of gear systems and components like camshafts, which optimize motion and efficiency in machinery.
- Architecture:
Architects often use ellipses in the design of structures such as arches, domes, and buildings. Calculating the perimeter helps in material estimation and structural integrity assessments.
- Sports:
Elliptical tracks and fields are common in sports like cycling and athletics. Knowing the perimeter is important for designing tracks and measuring distances for training and competitions.
- Technology:
In optics, elliptical mirrors and lenses are used to focus light and other forms of energy. Calculations of the ellipse perimeter contribute to the precision of these devices.
- Recreational Facilities:
Elliptical swimming pools and racetracks provide unique aesthetic and functional benefits. The perimeter calculation is vital for construction and maintenance.
- Art and Design:
Elliptical shapes are prevalent in various forms of art and design, including jewelry, furniture, and visual art. Understanding the perimeter aids in creating balanced and harmonious designs.
Here are some specific examples illustrating the practical use of ellipse perimeter calculations:
- Example 1: Satellite Orbits
To maintain a satellite in a stable orbit, engineers must calculate the perimeter of its elliptical path around Earth. This ensures the satellite remains within its designated trajectory.
- Example 2: Elliptical Racetracks
Designing an elliptical racetrack requires precise perimeter measurements to ensure accurate distance markers for athletes. This is critical for fairness in competitive events.
- Example 3: Optical Instruments
Elliptical mirrors used in telescopes and microscopes require exact perimeter calculations to enhance their focusing abilities, leading to clearer and more accurate observations.
- Example 4: Elliptical Pools
Constructing an elliptical swimming pool involves determining the perimeter to estimate the amount of materials needed for the pool's edge, ensuring cost-effective construction.
- Example 5: Jewelry Design
Designers create elliptical jewelry pieces that require precise perimeter measurements to fit stones accurately and maintain aesthetic proportions.
Tại sao không có phương trình cho chu vi của hình elip‽
READ MORE:
Độ Dài Cung: Chu Vi của Hình Elip | Bài Giảng 36 | Tính Toán Vectơ cho Kỹ Sư