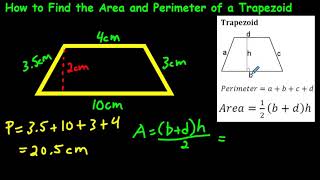
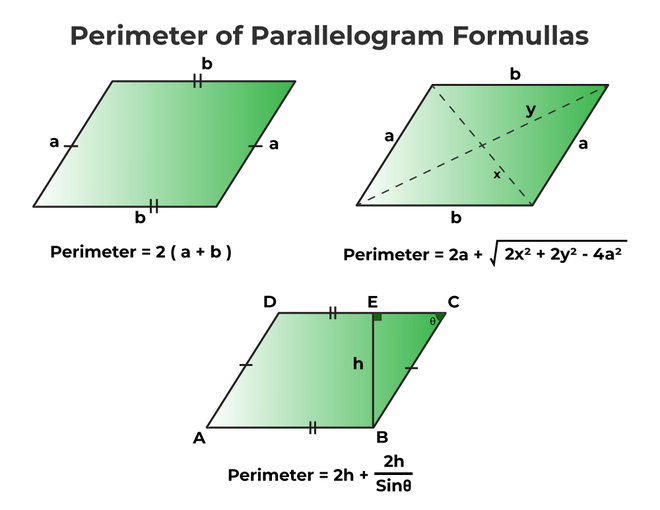
Topic find the perimeter and area of the polygon shown below: Welcome to our comprehensive guide on finding the perimeter and area of polygons. In this article, we will explore the various types of polygons, their properties, and provide step-by-step instructions for calculating their perimeter and area. Let's dive in and simplify the process of understanding and solving these mathematical problems.
Table of Content
- Perimeter and Area of a Polygon
- Introduction to Polygons
- Types of Polygons
- Basic Properties of Polygons
- Understanding Perimeter and Area
- Formulas for Perimeter of Polygons
- Formulas for Area of Polygons
- Step-by-Step Guide to Calculate Perimeter
- Step-by-Step Guide to Calculate Area
- Examples of Finding Perimeter
- Examples of Finding Area
- Practical Applications
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Complex Polygons
- Frequently Asked Questions
- Conclusion
- YOUTUBE:
Perimeter and Area of a Polygon
To find the perimeter and area of a polygon, follow the steps below:
Finding the Perimeter
The perimeter of a polygon is the sum of the lengths of all its sides. If the polygon has n sides, and the lengths of the sides are a1, a2, ..., an, then the perimeter P is given by:
\( P = a_1 + a_2 + \cdots + a_n \)
Finding the Area
The area of a polygon can be found using various methods depending on the type of polygon and the available information. Here are some common methods:
Area of a Regular Polygon
A regular polygon has all sides of equal length and all interior angles of equal measure. The area A of a regular polygon with n sides, each of length a, and an apothem r (the distance from the center to the midpoint of a side) is given by:
\( A = \frac{1}{2} \times n \times a \times r \)
Area of an Irregular Polygon Using Coordinates
If the coordinates of the vertices of the polygon are known, the area can be calculated using the Shoelace formula. For a polygon with vertices \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\), the area A is given by:
\( A = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) + (x_n y_1 - y_n x_1) \right| \)
Example Calculation
Consider a polygon with vertices at the following coordinates: \((1, 2)\), \((4, 5)\), \((7, 8)\), and \((1, 8)\). To find the area:
- List the coordinates cyclically: \((1, 2), (4, 5), (7, 8), (1, 8), (1, 2)\).
- Apply the Shoelace formula:
| \( x \) | 1 | 4 | 7 | 1 | 1 |
| \( y \) | 2 | 5 | 8 | 8 | 2 |
| \( x \times y \) (sum part) | \( 1 \times 5 = 5 \) | \( 4 \times 8 = 32 \) | \( 7 \times 8 = 56 \) | \( 1 \times 2 = 2 \) | |
| \( y \times x \) (subtract part) | \( 2 \times 4 = 8 \) | \( 5 \times 7 = 35 \) | \( 8 \times 1 = 8 \) | \( 8 \times 1 = 8 \) |
Summing these values:
\( \left| (5 + 32 + 56 + 2) - (8 + 35 + 8 + 8) \right| = \left| 95 - 59 \right| = 36 \)
Thus, the area is:
\( A = \frac{1}{2} \times 36 = 18 \text{ square units} \)
By following these steps, you can calculate the perimeter and area of any polygon given the necessary measurements.

READ MORE:
Introduction to Polygons
Polygons are fundamental shapes in geometry, defined as closed, two-dimensional figures with straight sides. These sides, or edges, are connected by vertices, forming a variety of shapes such as triangles, quadrilaterals, pentagons, and more. Understanding polygons is essential for comprehending more complex geometric concepts.
Key characteristics of polygons include:
- Number of Sides: Polygons are classified based on the number of sides they possess. For example, a triangle has three sides, a quadrilateral has four, and a pentagon has five.
- Angles: The internal angles of a polygon are the angles formed by two adjacent sides. The sum of the internal angles depends on the number of sides and can be calculated using the formula: \((n-2) \times 180^\circ\), where n is the number of sides.
- Vertices: These are the points where two sides of a polygon meet. The number of vertices in a polygon is equal to the number of sides.
Polygons can be categorized into regular and irregular polygons:
- Regular Polygons: All sides and angles are equal. Examples include equilateral triangles and squares.
- Irregular Polygons: Sides and angles are not equal. Examples include scalene triangles and rectangles.
Polygons are utilized in various practical applications, including architecture, engineering, and computer graphics, making them a crucial topic in both academic and real-world contexts.
Types of Polygons
Polygons are closed, two-dimensional shapes with straight sides. They are classified based on the number of sides they have. Here are the most common types:
- Triangle: A polygon with three sides and three angles. Examples include equilateral, isosceles, and scalene triangles.
- Quadrilateral: A polygon with four sides. Types include squares, rectangles, trapezoids, and rhombuses.
- Pentagon: A polygon with five sides. Regular pentagons have all sides and angles equal.
- Hexagon: A polygon with six sides. A regular hexagon has six equal sides and angles.
- Heptagon: A polygon with seven sides. Regular heptagons have seven equal sides and angles.
- Octagon: A polygon with eight sides. Regular octagons are commonly seen in stop signs.
- Nonagon: A polygon with nine sides. A regular nonagon has nine equal sides and angles.
- Decagon: A polygon with ten sides. Regular decagons have ten equal sides and angles.
Polygons can also be categorized as regular or irregular:
- Regular Polygons: All sides and angles are equal. Examples include equilateral triangles and squares.
- Irregular Polygons: Sides and angles are not all equal. Examples include scalene triangles and rectangles.
Understanding these basic types is crucial for learning how to calculate their perimeter and area.
Basic Properties of Polygons
A polygon is a two-dimensional geometric figure with a finite number of straight sides that are connected to form a closed shape. Here are some basic properties of polygons:
- Sides: Polygons are made up of line segments called sides. The number of sides determines the name of the polygon (e.g., triangle, quadrilateral, pentagon).
- Vertices: The points where two sides meet are called vertices (singular: vertex).
- Angles: Polygons have interior and exterior angles. The sum of the interior angles of a polygon with \(n\) sides is given by \( (n-2) \times 180^\circ \).
- Diagonals: A diagonal is a line segment that connects two non-adjacent vertices. The number of diagonals in a polygon with \(n\) sides is given by \( \frac{n(n-3)}{2} \).
Regular and Irregular Polygons
Polygons can be classified as regular or irregular:
- Regular Polygon: All sides and angles are equal. Examples include equilateral triangles and squares.
- Irregular Polygon: Sides and angles are not equal. Examples include scalene triangles and rectangles.
Convex and Concave Polygons
Another classification of polygons is based on their shape:
- Convex Polygon: All interior angles are less than 180°, and no vertices point inward.
- Concave Polygon: At least one interior angle is greater than 180°, and some vertices point inward.
Formulas for Perimeter and Area
The perimeter and area are two essential properties of polygons:
- Perimeter: The perimeter is the total length of all the sides of a polygon. For a regular polygon, it is given by: \[ P = n \times a \] where \( n \) is the number of sides, and \( a \) is the length of one side. For irregular polygons, the perimeter is the sum of the lengths of all sides: \[ P = \sum_{i=1}^{n} a_i \] where \( a_i \) are the side lengths.
- Area: The area is the space enclosed within the sides of a polygon. The formula varies depending on the type of polygon. For a regular polygon, it is: \[ A = \frac{1}{4} n a^2 \cot \left(\frac{\pi}{n}\right) \] For other polygons, methods like triangulation, the Shoelace theorem, or specific formulas for triangles, rectangles, etc., are used.
Understanding these basic properties helps in identifying and working with various types of polygons effectively.
Understanding Perimeter and Area
Understanding the concepts of perimeter and area is fundamental in geometry, especially when dealing with polygons. Both terms describe different aspects of a polygon and are crucial for various applications in mathematics, engineering, and real life.
Perimeter of a Polygon
The perimeter of a polygon is the total length of its sides. To find the perimeter, you simply add the lengths of all the sides together. For regular polygons, where all sides are of equal length, the formula is straightforward:
For a polygon with \( n \) sides, each of length \( a \):
\[ P = n \times a \]
For irregular polygons, sum the lengths of all individual sides:
\[ P = a_1 + a_2 + a_3 + \ldots + a_n \]
Area of a Polygon
The area of a polygon is the measure of the space enclosed within its sides. The method to calculate the area depends on the type of polygon.
Area of Regular Polygons
For a regular polygon (all sides and angles are equal), the area can be calculated using the formula:
\[ A = \frac{1}{4} n a^2 \cot\left(\frac{\pi}{n}\right) \]
where \( n \) is the number of sides and \( a \) is the side length.
Area of Irregular Polygons
For irregular polygons, one common method is to divide the polygon into simpler shapes (like triangles) and sum their areas. If the coordinates of the vertices are known, the area can be found using the Shoelace Theorem:
\[ A = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - x_{i+1} y_i) + (x_n y_1 - x_1 y_n) \right| \]
Examples
Consider a square and a triangle as examples:
Square
- Perimeter: For a square with side length \( a \), the perimeter is \( P = 4a \).
- Area: The area of a square is \( A = a^2 \).
Triangle
- Perimeter: For a triangle with side lengths \( a, b, \) and \( c \), the perimeter is \( P = a + b + c \).
- Area: Using Heron's formula, the area can be found as: \[ s = \frac{a + b + c}{2} \] \[ A = \sqrt{s(s-a)(s-b)(s-c)} \]
Applications
Understanding the perimeter and area is essential in various fields such as architecture, engineering, and everyday tasks. For instance, calculating the amount of fencing needed for a garden (perimeter) or determining the amount of paint required for a wall (area).

Formulas for Perimeter of Polygons
The perimeter of a polygon is the total length of all its sides. To find the perimeter, you simply add up the lengths of each side. The formula varies slightly depending on the type of polygon:
- Regular Polygon: A regular polygon has all sides of equal length and all interior angles equal.
- Formula: \( P = n \times s \)
- Where:
- \( P \) = Perimeter
- \( n \) = Number of sides
- \( s \) = Length of one side
- Irregular Polygon: An irregular polygon has sides of different lengths.
- Formula: \( P = s_1 + s_2 + s_3 + \ldots + s_n \)
- Where:
- \( P \) = Perimeter
- \( s_1, s_2, s_3, \ldots, s_n \) = Lengths of each side
- Special Case - Rectangle: A rectangle has opposite sides of equal length.
- Formula: \( P = 2(l + w) \)
- Where:
- \( P \) = Perimeter
- \( l \) = Length
- \( w \) = Width
- Special Case - Square: A square is a regular polygon with four equal sides.
- Formula: \( P = 4s \)
- Where:
- \( P \) = Perimeter
- \( s \) = Length of one side
Here are some example calculations for better understanding:
- Example 1: Find the perimeter of a regular hexagon with each side measuring 6 cm.
- Solution: \( P = 6 \times 6 = 36 \, \text{cm} \)
- Example 2: Find the perimeter of a rectangle with length 10 cm and width 5 cm.
- Solution: \( P = 2(10 + 5) = 2 \times 15 = 30 \, \text{cm} \)
- Example 3: Find the perimeter of an irregular polygon with sides measuring 3 cm, 4 cm, 5 cm, and 6 cm.
- Solution: \( P = 3 + 4 + 5 + 6 = 18 \, \text{cm} \)
Formulas for Area of Polygons
Calculating the area of a polygon depends on whether the polygon is regular (all sides and angles are equal) or irregular. Below are the formulas and steps to calculate the area for various types of polygons:
1. Regular Polygons
For regular polygons, where all sides and angles are equal, the area can be calculated using the following formulas:
- Using the side length \(a\):
The area \(A\) of a regular polygon with \(n\) sides each of length \(a\) is given by:
\[ A = \frac{n \cdot a^2}{4} \cot\left(\frac{\pi}{n}\right) \]
- Using the apothem \(r_i\):
The apothem is the distance from the center to the midpoint of one of its sides.
\[ A = \frac{1}{2} \cdot \text{Perimeter} \cdot r_i \]
\[ \text{or} \]
\[ A = \frac{n \cdot a \cdot r_i}{2} \]
- Using the circumradius \(r_c\):
The circumradius is the radius of the circle that passes through all the vertices of the polygon.
\[ A = \frac{n \cdot r_c^2 \cdot \sin\left(\frac{2\pi}{n}\right)}{2} \]
2. Irregular Polygons
For irregular polygons, the area can be calculated by dividing the polygon into simpler shapes such as triangles, then finding the area of each triangle and summing them up. Here are some methods:
- Using vertices coordinates:
If the coordinates of the vertices \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\) are known, the area \(A\) can be calculated using the Shoelace formula:
\[ A = \frac{1}{2} \left| \sum_{i=1}^{n} (x_i \cdot y_{i+1} - y_i \cdot x_{i+1}) \right| \]
where \((x_{n+1}, y_{n+1})\) is the same as \((x_1, y_1)\).
- Dividing into triangles:
For a polygon that can be divided into triangles, use the area formula for triangles and sum the areas:
\[ A = \sum \text{Area of each triangle} \]
For example, using Heron's formula for each triangle formed by sides \(a\), \(b\), and \(c\):
\[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
where \(s\) is the semi-perimeter: \( s = \frac{a+b+c}{2} \).
Examples
Here are some examples to illustrate the calculations:
- Example 1: Regular Hexagon
A regular hexagon with side length \(a = 6\):
\[ A = \frac{6 \cdot 6^2}{4} \cot\left(\frac{\pi}{6}\right) = \frac{6 \cdot 36}{4} \cdot \frac{\sqrt{3}}{3} = 54\sqrt{3} \approx 93.53 \text{ square units} \]
- Example 2: Irregular Polygon using Coordinates
Polygon with vertices at \((2,1)\), \((4,5)\), \((7,8)\), and \((6,3)\):
\[ A = \frac{1}{2} \left| (2 \cdot 5 + 4 \cdot 8 + 7 \cdot 3 + 6 \cdot 1) - (1 \cdot 4 + 5 \cdot 7 + 8 \cdot 6 + 3 \cdot 2) \right| \]
\[ A = \frac{1}{2} \left| (10 + 32 + 21 + 6) - (4 + 35 + 48 + 6) \right| \]
\[ A = \frac{1}{2} \left| 69 - 93 \right| = \frac{1}{2} \times 24 = 12 \text{ square units} \]
Conclusion
Understanding and applying these formulas allows for accurate calculation of the area for both regular and irregular polygons, which is essential in various fields such as architecture, engineering, and mathematics.
Step-by-Step Guide to Calculate Perimeter
The perimeter of a polygon is the total length of its boundaries. Here is a detailed, step-by-step guide to help you calculate the perimeter of different types of polygons.
-
Identify the Type of Polygon
First, determine whether the polygon is regular (all sides and angles are equal) or irregular (sides and angles are not necessarily equal).
-
Measure the Length of Each Side
If the polygon is irregular, measure the length of each side individually. For regular polygons, measure the length of one side since all sides are equal.
-
Apply the Appropriate Formula
Use the specific formula based on the type of polygon:
- Regular Polygon: \( P = n \times a \)
- Irregular Polygon: \( P = \sum_{i=1}^{n} a_i \)
- Using Coordinates: \( P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \)
-
Sum the Lengths
For an irregular polygon, add the lengths of all the sides. For a regular polygon, multiply the number of sides by the length of one side.
-
Convert Units if Necessary
Ensure all side lengths are in the same unit before summing them up. Convert units if necessary to maintain consistency.
-
Examples
-
Example 1: Square
If each side of a square is 5 units, then the perimeter \( P = 4 \times 5 = 20 \) units.
-
Example 2: Irregular Quadrilateral
If the side lengths are 3 units, 4 units, 5 units, and 6 units, then the perimeter \( P = 3 + 4 + 5 + 6 = 18 \) units.
-
Example 3: Using Coordinates
For a polygon with vertices at (0, 0), (0, 3), (3, 3), and (3, 0), calculate each side's length using the distance formula and sum them:
\[
\text{Length of side } AB = \sqrt{(0-0)^2 + (3-0)^2} = 3 \text{ units}
\]\[
\text{Length of side } BC = \sqrt{(3-0)^2 + (3-3)^2} = 3 \text{ units}
\]\[
\text{Length of side } CD = \sqrt{(3-3)^2 + (0-3)^2} = 3 \text{ units}
\]\[
\text{Length of side } DA = \sqrt{(0-3)^2 + (0-0)^2} = 3 \text{ units}
\]Thus, the perimeter \( P = 3 + 3 + 3 + 3 = 12 \) units.
-
By following these steps, you can calculate the perimeter of any polygon accurately.
Step-by-Step Guide to Calculate Area
Calculating the area of a polygon can vary based on whether the polygon is regular (all sides and angles are equal) or irregular. Here is a step-by-step guide for both cases:
For Regular Polygons
The formula for the area of a regular polygon (a polygon with equal sides and angles) is given by:
\( A = \frac{n \cdot s^2}{4} \cdot \cot \left(\frac{\pi}{n}\right) \)
where:
- \( A \) is the area
- \( n \) is the number of sides
- \( s \) is the length of one side
- Determine the number of sides (\( n \)) of the polygon.
- Measure the length of one side (\( s \)).
- Substitute these values into the formula:
- Calculate \( \cot \left(\frac{\pi}{n}\right) \) using a calculator.
- Compute the area using the formula \( A = \frac{n \cdot s^2}{4} \cdot \cot \left(\frac{\pi}{n}\right) \).
Example:
To find the area of a regular hexagon (6 sides) with a side length of 4:
\( A = \frac{6 \cdot 4^2}{4} \cdot \cot \left(\frac{\pi}{6}\right) \)
After calculating, you get:
\( A = 6 \cdot 4 \cdot 4 \cdot \cot (\frac{\pi}{6}) / 4 \)
Therefore, the area is:
\( A = 24 \cdot \sqrt{3} / 4 \approx 41.57 \)
For Irregular Polygons
For an irregular polygon, one of the common methods is to use the vertices' coordinates. The formula for the area when the coordinates of the vertices are known is:
\( A = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) + (x_n y_1 - y_n x_1) \right| \)
where:
- \( (x_i, y_i) \) are the coordinates of the vertices
- List the coordinates of all vertices in order.
- Apply the coordinates to the formula.
- Calculate the area using the determinant method.
Example:
For a polygon with vertices at (2,1), (4,5), (7,8), and (6,3):
\( A = \frac{1}{2} \left| 2 \cdot 5 + 4 \cdot 8 + 7 \cdot 3 + 6 \cdot 1 - (1 \cdot 4 + 5 \cdot 7 + 8 \cdot 6 + 3 \cdot 2) \right| \)
After calculating, you get:
\( A = \frac{1}{2} \left| 10 + 32 + 21 + 6 - (4 + 35 + 48 + 6) \right| = \frac{1}{2} \left| 69 - 93 \right| = \frac{1}{2} \left| -24 \right| = 12 \)
Using the Shoelace Formula
The above example employs the Shoelace formula, a common method for finding the area of an irregular polygon.
These methods cover the basic approaches for calculating the area of regular and irregular polygons. Practice with different sets of data to become proficient in these calculations.

Examples of Finding Perimeter
Finding the perimeter of a polygon involves summing the lengths of all its sides. Below are some detailed examples to illustrate how to calculate the perimeter for different types of polygons.
Example 1: Regular Polygon
Consider a regular hexagon where all sides are of equal length.
- Number of sides, \( n = 6 \)
- Length of one side, \( a = 5 \, \text{units} \)
The perimeter \( P \) is calculated as:
\[
P = n \times a = 6 \times 5 = 30 \, \text{units}
\]
Example 2: Irregular Polygon
Consider an irregular polygon with the following side lengths:
- Side 1: \( 7 \, \text{units} \)
- Side 2: \( 5 \, \text{units} \)
- Side 3: \( 10 \, \text{units} \)
- Side 4: \( 6 \, \text{units} \)
- Side 5: \( 8 \, \text{units} \)
The perimeter \( P \) is calculated as:
\[
P = 7 + 5 + 10 + 6 + 8 = 36 \, \text{units}
\]
Example 3: Polygon with Given Vertices
To find the perimeter of a polygon with vertices, calculate the distance between consecutive vertices using the distance formula. Consider a square with vertices at \( (0,0) \), \( (0,3) \), \( (3,3) \), and \( (3,0) \).
- Distance between \( (0,0) \) and \( (0,3) \) is \( 3 \, \text{units} \)
- Distance between \( (0,3) \) and \( (3,3) \) is \( 3 \, \text{units} \)
- Distance between \( (3,3) \) and \( (3,0) \) is \( 3 \, \text{units} \)
- Distance between \( (3,0) \) and \( (0,0) \) is \( 3 \, \text{units} \)
The perimeter \( P \) is calculated as:
\[
P = 3 + 3 + 3 + 3 = 12 \, \text{units}
\]
Example 4: Finding Missing Length in Irregular Polygon
Given an irregular polygon ABCDEF with sides \( AB = 3 \, \text{units} \), \( BC = 4 \, \text{units} \), \( CD = 6 \, \text{units} \), \( DE = 2 \, \text{units} \), \( EF = 1.5 \, \text{units} \), and the total perimeter \( P = 18.5 \, \text{units} \), find the missing side \( FA \).
Set up the equation:
\[
P = AB + BC + CD + DE + EF + FA
\]
Solving for \( FA \):
\[
18.5 = 3 + 4 + 6 + 2 + 1.5 + FA \\
FA = 18.5 - (3 + 4 + 6 + 2 + 1.5) = 2 \, \text{units}
\]
Thus, the missing side \( FA \) is \( 2 \, \text{units} \).
These examples illustrate various methods for calculating the perimeter of different polygons, whether they are regular, irregular, or given by vertices.
Examples of Finding Area
To understand how to find the area of a polygon, let's look at a few examples using different methods for both regular and irregular polygons.
Example 1: Regular Polygon
Consider a regular hexagon (6-sided polygon) with a side length of 4 units.
- First, note the formula for the area of a regular polygon:
\[
\text{Area} = \frac{n \times a^2}{4} \times \cot\left(\frac{\pi}{n}\right)
\]
where \( n \) is the number of sides, and \( a \) is the length of one side. - Substitute the given values into the formula:
\[
\text{Area} = \frac{6 \times 4^2}{4} \times \cot\left(\frac{\pi}{6}\right)
\] - Calculate the cotangent and simplify:
\[
\text{Area} = \frac{6 \times 16}{4} \times \cot\left(30^\circ\right)
\]
\[
\text{Area} = 24 \times \sqrt{3}
\] - Thus, the area of the hexagon is:
\[
\text{Area} = 24\sqrt{3} \text{ square units}
\]
Example 2: Irregular Polygon
For an irregular polygon, you can divide it into simpler shapes, such as triangles and rectangles, find their areas, and then sum them up. Let's take an irregular pentagon divided into a rectangle and a triangle.
- The rectangle has a length of 10 units and a width of 4 units.
- The triangle has a base of 6 units and a height of 4 units.
To find the total area:
- Calculate the area of the rectangle:
\[
\text{Area}_{\text{rectangle}} = \text{length} \times \text{width} = 10 \times 4 = 40 \text{ square units}
\] - Calculate the area of the triangle:
\[
\text{Area}_{\text{triangle}} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 6 \times 4 = 12 \text{ square units}
\] - Add the areas of both shapes:
\[
\text{Total Area} = \text{Area}_{\text{rectangle}} + \text{Area}_{\text{triangle}} = 40 + 12 = 52 \text{ square units}
\]
Example 3: Using Coordinates
For polygons where the vertices' coordinates are known, use the Shoelace formula. Consider a polygon with vertices at (2, 1), (4, 5), (7, 8), and (6, 3).
- List the coordinates in a cyclic order, closing the polygon by repeating the first point at the end:
\[
(2, 1), (4, 5), (7, 8), (6, 3), (2, 1)
\] - Apply the Shoelace formula:
\[
\text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) \right|
\] - Calculate the determinant for each vertex pair:
\[
\text{Area} = \frac{1}{2} \left| (2 \cdot 5 + 4 \cdot 8 + 7 \cdot 3 + 6 \cdot 1) - (1 \cdot 4 + 5 \cdot 7 + 8 \cdot 6 + 3 \cdot 2) \right|
\]
\[
\text{Area} = \frac{1}{2} \left| (10 + 32 + 21 + 6) - (4 + 35 + 48 + 6) \right|
\]
\[
\text{Area} = \frac{1}{2} \left| 69 - 93 \right| = \frac{1}{2} \left| -24 \right| = 12 \text{ square units}
\]
These examples demonstrate how to find the area of various types of polygons using different methods.
Practical Applications
Understanding the perimeter and area of polygons is crucial in various practical applications. Here are some key examples:
- Architecture and Construction: Calculating the perimeter helps in determining the amount of materials needed for the boundary, such as fencing or walls. The area calculation is essential for flooring, tiling, and allocating space within buildings.
- Landscaping: Gardeners and landscapers use perimeter and area calculations to design and layout gardens, lawns, and parks. Knowing the perimeter helps in planning the fencing, while the area is used to calculate the amount of soil, seeds, or grass needed.
- Urban Planning: City planners use these measurements to design roads, parks, and public spaces, ensuring optimal use of available land. Accurate area calculations are crucial for zoning and development planning.
- Manufacturing: In the production of various products, such as metal sheets or fabrics, understanding the area is essential to minimize waste and cost. The perimeter helps in the cutting process and material handling.
- Sports Fields: The design and construction of sports fields, such as football or basketball courts, rely on accurate perimeter and area calculations to meet regulation sizes and ensure fair play.
- Art and Design: Artists and designers use these calculations to create proportional and aesthetically pleasing works, from sculptures to graphic designs.
Step-by-Step Example: Landscaping a Garden
- Measure the Garden Plot: Suppose you have a rectangular garden plot of 20 meters in length and 15 meters in width.
- Calculate the Perimeter:
The perimeter \(P\) of a rectangle is given by:
\[ P = 2 \times ( \text{length} + \text{width} ) \]
Substituting the values:
\[ P = 2 \times (20 + 15) = 2 \times 35 = 70 \text{ meters} \]
- Calculate the Area:
The area \(A\) of a rectangle is given by:
\[ A = \text{length} \times \text{width} \]
Substituting the values:
\[ A = 20 \times 15 = 300 \text{ square meters} \]
- Application:
With the perimeter known, you can plan for 70 meters of fencing around the garden. The area helps you determine that you need enough seeds or sod for 300 square meters of lawn. Additionally, knowing the area helps estimate the amount of soil and compost required for planting.
Example in Construction: Flooring a Room
- Measure the Room: Suppose the room is a rectangular shape with a length of 10 meters and a width of 8 meters.
- Calculate the Perimeter:
\[ P = 2 \times (10 + 8) = 2 \times 18 = 36 \text{ meters} \]
- Calculate the Area:
\[ A = 10 \times 8 = 80 \text{ square meters} \]
- Application:
The perimeter helps in estimating the length of baseboards needed for the room, while the area calculation is essential to determine the amount of flooring material required.
Common Mistakes and How to Avoid Them
When calculating the perimeter and area of polygons, there are several common mistakes that can lead to incorrect results. Below are some of these mistakes along with tips on how to avoid them:
-
Incorrectly Adding Side Lengths:
To avoid mistakes when calculating the perimeter, ensure you add all the side lengths correctly. Double-check each side length and ensure no side is missed.
-
Confusing Perimeter and Area:
The perimeter is the total distance around the polygon, while the area is the space enclosed within it. Always use the correct formula for each:
- Perimeter of a polygon: \( P = \sum_{i=1}^{n} s_i \) where \( s_i \) are the side lengths.
- Area of a regular polygon: \( A = \frac{1}{2} \times P \times a \) where \( P \) is the perimeter and \( a \) is the apothem.
-
Incorrect Use of Units:
Always ensure that the units used for all measurements are consistent. If side lengths are in meters, the perimeter will be in meters and the area in square meters.
-
Incorrect Formula Application:
Different polygons have different area formulas. For example:
- Rectangle: \( A = l \times w \)
- Triangle: \( A = \frac{1}{2} \times b \times h \)
- Trapezoid: \( A = \frac{1}{2} \times (b_1 + b_2) \times h \)
Make sure to use the formula that corresponds to the shape you are working with.
-
Omitting Heights or Apothem:
When calculating areas, especially for shapes like triangles and trapezoids, forgetting to include the height or apothem can result in incorrect calculations. Always identify and correctly use these measurements.
-
Misidentifying Shape Type:
Regular polygons have equal side lengths and angles, whereas irregular polygons do not. Ensure you correctly identify the type of polygon to apply the appropriate formula.
By being aware of these common mistakes and following the steps above, you can ensure more accurate calculations of the perimeter and area of polygons.
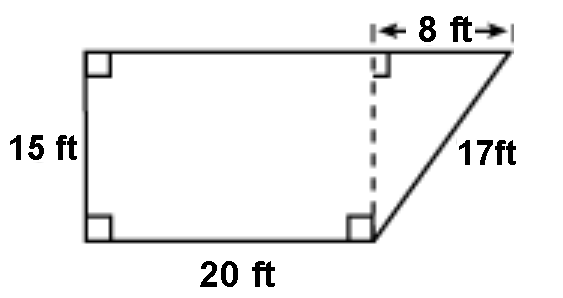
Advanced Techniques for Complex Polygons
Calculating the perimeter and area of complex polygons often involves more advanced techniques and mathematical principles. Here are some methods to tackle these challenges:
1. Decomposing into Simpler Shapes
One of the most effective techniques is to decompose a complex polygon into simpler shapes such as triangles, rectangles, and other regular polygons. This makes it easier to calculate the area and perimeter.
- Identify the simpler shapes within the polygon.
- Calculate the area and perimeter of each simpler shape.
- Sum the areas to get the total area of the complex polygon.
- Sum the relevant sides to get the perimeter.
For example, if you have a polygon that can be divided into a triangle and a rectangle, calculate the area of both shapes and add them together.
2. Using the Shoelace Formula
The Shoelace Formula, also known as Gauss's area formula, is a mathematical algorithm to find the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane.
- List the coordinates of the vertices in order.
- Apply the formula:
\[
\text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} + x_n y_1) - \sum_{i=1}^{n-1} (y_i x_{i+1} + y_n x_1) \right|
\] - Calculate the determinant sums and find the area.
3. Using Trigonometry for Regular Polygons
For regular polygons, trigonometric functions can simplify the calculations:
- Calculate the perimeter:
\[
\text{Perimeter} = n \times s
\]
where \( n \) is the number of sides and \( s \) is the length of each side. - Calculate the area using the apothem:
\[
\text{Area} = \frac{1}{2} \times \text{Perimeter} \times \text{Apothem}
\]
4. Applying Coordinate Geometry
For polygons plotted on a coordinate plane, you can use coordinate geometry to find distances between points (sides) and angles:
- Use the distance formula to calculate the length of each side:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Calculate the area of each constituent shape using appropriate formulas.
- Sum the areas for the total area.
5. Using Integration for Irregular Polygons
For highly irregular polygons, calculus and integration can be used. This is especially useful when dealing with curves or boundaries not defined by straight lines:
- Set up the integral for the area based on the boundaries of the polygon.
- Calculate the integral to find the total area enclosed by the polygon.
These advanced techniques allow for more accurate calculations and are essential for dealing with complex polygon shapes. Practicing these methods with various examples will improve your proficiency in handling complex polygons.
Frequently Asked Questions
-
What is the Perimeter of a Polygon?
The perimeter of a polygon is the total length of the boundary of the polygon. It is calculated by adding the lengths of all its sides and is expressed in linear units such as meters, centimeters, inches, or feet.
-
How to Find the Perimeter of a Polygon?
- Determine if the polygon is regular (all sides and angles are equal) or irregular.
- For a regular polygon, use the formula:
\[ \text{Perimeter} = (\text{number of sides}) \times (\text{length of one side}) - For an irregular polygon, add the lengths of all the sides.
- Ensure that all side lengths are in the same unit before calculating.
-
What is the Difference Between the Area and Perimeter of Polygons?
The perimeter of a polygon is the total length of its boundary, while the area is the space enclosed within the polygon. The perimeter is measured in linear units, whereas the area is measured in square units.
-
How to Find the Perimeter of Polygons with Vertices?
- Calculate the distance between each pair of consecutive vertices using the distance formula:
\[ D = \sqrt{{(x_2 - x_1)}^2 + {(y_2 - y_1)}^2} \] - Add the distances to find the total perimeter.
- Calculate the distance between each pair of consecutive vertices using the distance formula:
-
Can the Perimeter of a Polygon be Negative?
No, the perimeter of a polygon cannot be negative. It is always a positive value, as it represents the total length of the polygon's sides.
-
How Does Changing the Length of a Side Affect the Perimeter?
Changing the length of any side of a polygon will directly affect the total perimeter. Increasing the length of a side will increase the perimeter, while decreasing the length will decrease the perimeter.
Conclusion
Understanding the concepts of perimeter and area is essential for solving many real-world problems involving polygons. By mastering the formulas and techniques discussed, you can confidently tackle a wide range of geometric challenges.
Here's a summary of the key points covered in this guide:
- Introduction to Polygons: We explored the basic definition and properties of polygons, including the different types and their characteristics.
- Formulas for Perimeter: We provided the general formulas for calculating the perimeter of various types of polygons, such as regular and irregular polygons.
- Formulas for Area: We detailed the formulas for finding the area of different polygons, emphasizing the importance of knowing the specific type of polygon you're dealing with.
- Step-by-Step Guides: Detailed instructions were given to help you calculate the perimeter and area of polygons step-by-step, ensuring a clear understanding of the process.
- Examples: Practical examples were provided to illustrate the methods for finding the perimeter and area, helping to solidify your understanding through real-world applications.
- Advanced Techniques: We discussed advanced methods for dealing with complex polygons, including those with more sides or irregular shapes.
- Common Mistakes: Tips were given to help you avoid common pitfalls and errors when calculating perimeter and area.
By following this comprehensive guide, you should now have a solid foundation in understanding and calculating the perimeter and area of various polygons. Whether you're solving homework problems, working on projects, or simply exploring the fascinating world of geometry, the knowledge you've gained here will be invaluable.
Remember, practice is key to mastering these concepts. Keep working on different problems, and soon you'll find that calculating perimeter and area becomes second nature.
Thank you for taking the time to learn with us. We hope this guide has been helpful and informative, and we encourage you to continue exploring the wonderful world of polygons and geometry.
Tìm Diện Tích Đa Giác Đều Dựa Trên Bán Kính
READ MORE:
Xem video để tìm chu vi và diện tích của đa giác được hiển thị bên dưới. Hướng dẫn chi tiết và dễ hiểu.
Tìm chu vi và diện tích của đa giác được hiển thị bên dưới. 17 ft P = 72 feet; A = 300 feet vuông