Topic parallelogram perimeter and area: Dive into the fascinating world of geometry with our comprehensive guide on "Parallelogram Perimeter and Area," where mathematics meets real-world applications in an engaging and accessible manner.
Table of Content
- How to find the perimeter and area of a parallelogram?
- Basics of a Parallelogram
- Calculating the Area of a Parallelogram
- Understanding Parallelogram Perimeter
- YOUTUBE: Area of a parallelogram | Khan Academy
- Parallelogram Area with Given Sides and Angle
- Area Calculation Without Height
- Advanced Perimeter Formulas
- Practical Examples and Solved Problems
- FAQs and Common Misconceptions
How to find the perimeter and area of a parallelogram?
To find the perimeter and area of a parallelogram, follow these steps:
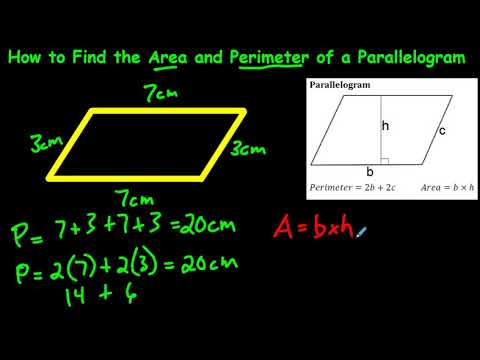
- Perimeter:
- Calculate the sum of all four sides of the parallelogram. Since opposite sides of a parallelogram are congruent, you can either add the lengths of two adjacent sides and multiply the result by 2, or add the lengths of all four sides.
- For example, if the lengths of two adjacent sides are 5 cm and 8 cm, the perimeter of the parallelogram would be (5 + 8) * 2 = 26 cm.
- Area:
- Measure the length of the base of the parallelogram (the side that is parallel to the height).
- Measure the perpendicular height of the parallelogram from the base to the opposite side.
- Multiply the length of the base by the height to find the area of the parallelogram.
- For example, if the base of the parallelogram is 6 cm and the height is 4 cm, the area would be 6 cm * 4 cm = 24 square cm.
READ MORE:
Basics of a Parallelogram
A parallelogram is a four-sided figure, or quadrilateral, where opposite sides are parallel and equal in length. This unique structure leads to several key properties:
- Opposite Sides: In a parallelogram, opposite sides are not only parallel but also of equal length.
- Opposite Angles: The angles opposite to each other in a parallelogram are equal in measure.
- Adjacent Angles: Any two adjacent angles in a parallelogram are supplementary, meaning they add up to 180 degrees.
- Diagonals: The diagonals of a parallelogram bisect each other, dividing each other into two equal parts.
- Sum of Angles: The sum of the interior angles in a parallelogram always adds up to 360 degrees.
These properties are fundamental to understanding the geometric nature of parallelograms and are essential for further exploration into their perimeter and area calculations.
In addition to these properties, it\"s important to note that squares, rectangles, and rhombuses are all specific types of parallelograms, each with additional unique properties.
Understanding the basics of a parallelogram is crucial for delving into more complex geometric calculations and solving problems related to area and perimeter, which will be explored in subsequent sections of this article.
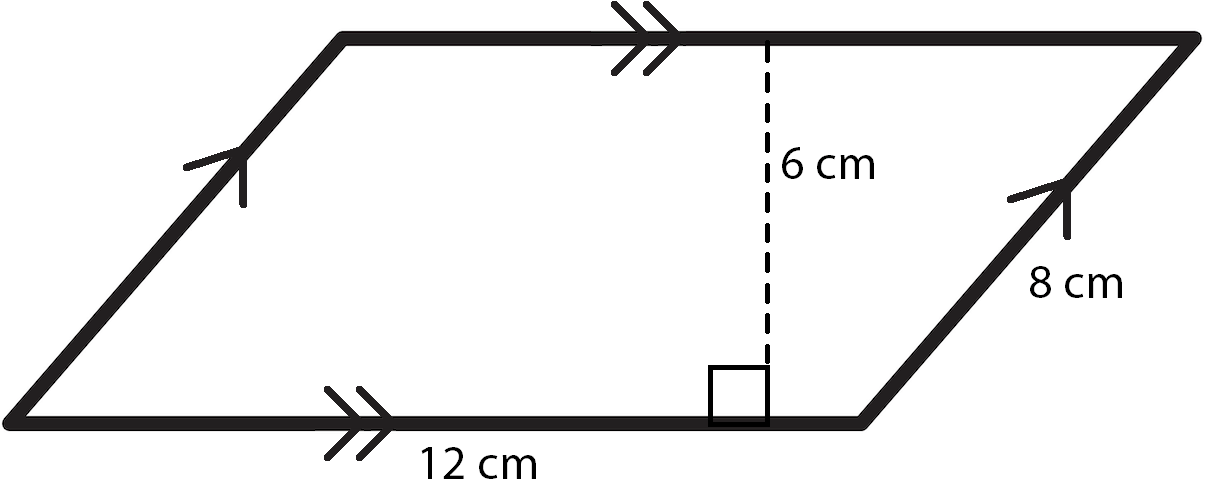
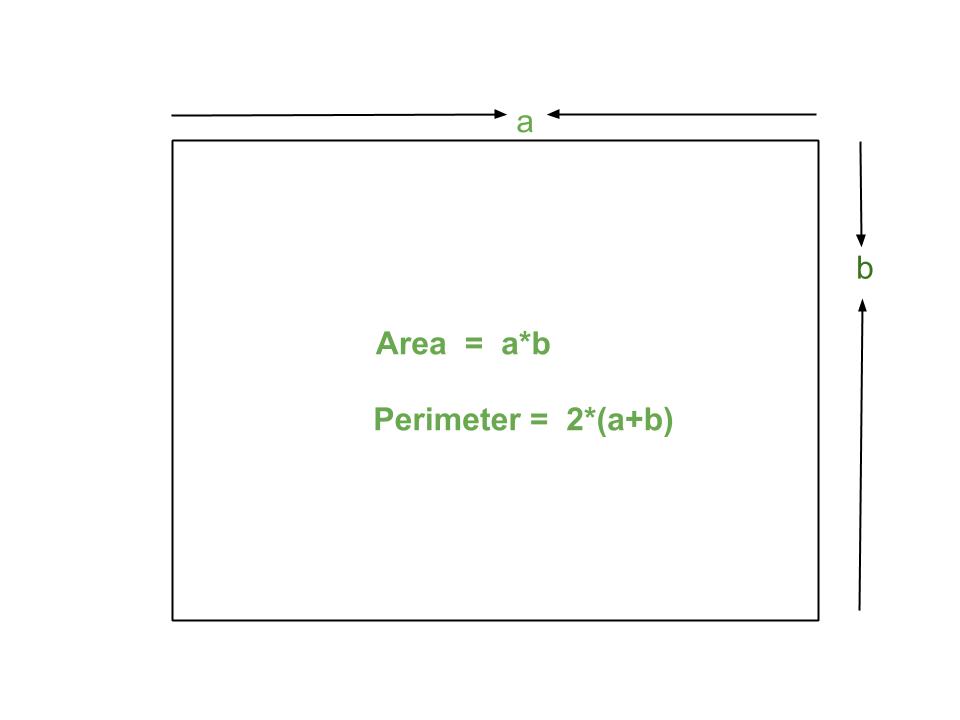
Calculating the Area of a Parallelogram
A parallelogram is a unique quadrilateral with two pairs of parallel sides. The area of a parallelogram is calculated using different formulas depending on the information available. The most common formula for finding the area is by multiplying the base and the height of the parallelogram.
The basic formula to calculate the area is:
- Area = base × height
This formula is similar to that for calculating the area of a rectangle. In a parallelogram, the height is always perpendicular to the base. For example, if a parallelogram has a base of 6 meters and a height of 3 meters, its area would be 18 square meters.
Beyond the basic method, there are other ways to calculate the area of a parallelogram, especially when different sets of information are known:
- Using the lengths of adjacent sides and the angle between them:
- Area = a × b × sin(angle)
- Using the lengths of diagonals and the angle between them:
- Area = ½ × diagonal1 × diagonal2 × sin(angle)
The first alternative method involves trigonometry, where \"a\" and \"b\" are the lengths of adjacent sides, and \"angle\" is the angle between these sides. The second method also uses trigonometry, where \"diagonal1\" and \"diagonal2\" are the lengths of the diagonals, and \"angle\" is the angle between the diagonals. In both cases, trigonometric functions play a key role in the calculation.
For practical application of these formulas, it is essential to understand the properties of parallelograms and the relationships between their sides, angles, and diagonals. This knowledge is vital for effectively applying these formulas in different scenarios.
Understanding Parallelogram Perimeter
The perimeter of a parallelogram is the total distance around its boundary. This geometric figure is unique in that its opposite sides are parallel and equal in length, a defining characteristic that directly influences how its perimeter is calculated. Let\"s explore how to determine the perimeter of a parallelogram, taking into consideration its fundamental properties and applying them in practical scenarios.
- Basic Properties: A parallelogram is a four-sided figure with opposite sides that are both parallel and equal in length. Additionally, opposite angles in a parallelogram are equal, and each pair of adjacent angles are supplementary, summing up to 180 degrees.
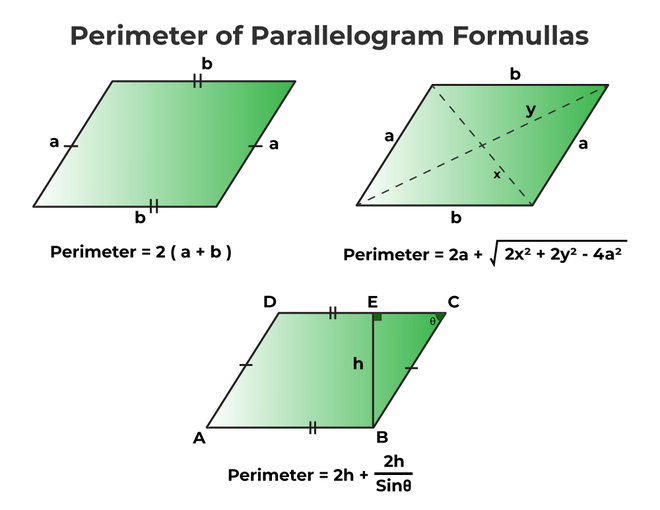
- Standard Perimeter Formula: The most common method to calculate the perimeter of a parallelogram involves using the lengths of its adjacent sides. If \"a\" and \"b\" represent the lengths of the adjacent sides, the perimeter (P) can be calculated using the formula: P = 2(a + b).
- Example Calculation: For instance, if one side of a parallelogram is 10 cm and the adjacent side is 5 cm, the perimeter is calculated as P = 2(10 + 5) = 30 cm.
In addition to the standard method, other ways of calculating the perimeter may involve the use of trigonometric functions, especially when dealing with angles and varying side lengths.
- Using Base, Height, and an Angle: In cases where the base (b), height (h), and an interior angle (θ) are known, the perimeter can be calculated using a modified formula: P = 2(b + h/cos θ), where θ is the angle between the base and the height.
These methods highlight the interplay between the unique properties of parallelograms and standard geometric formulas, providing a comprehensive approach to understanding and calculating the perimeter of this versatile shape.
Practical Application Examples
To solidify understanding, let\"s consider a practical example:
- Suppose a parallelogram has a base of 15 cm and a side length of 7 cm, the perimeter would be calculated as follows: Perimeter = 2(15 + 7) = 44 cm.
By exploring these various methods and examples, one can gain a deeper understanding of the geometric principles governing parallelograms and their perimeters.

Area of a parallelogram | Khan Academy
\"If you\'re fascinated by the symmetrical beauty of parallelograms, this video is a must-watch! Learn the secrets of this geometric wonder as we explore its angles, sides, and properties. Get ready to marvel at the mesmerizing world of parallelograms!\"
How to Find the Area of a Parallelogram
\"Unlock the mysteries of calculating the area with this engaging video! Dive into the fascinating world of shapes and measurements as we unravel the secrets of finding the area. Discover easy-to-follow techniques and watch your math skills soar to new heights!\"
Parallelogram Area with Given Sides and Angle
The area of a parallelogram can be calculated in various ways depending on the available information. When the lengths of the sides and the angle between them are known, specific formulas can be applied to determine the area. This method uses trigonometry principles to calculate the area, providing a versatile approach to understanding parallelogram geometry.
Understanding the Basics: A parallelogram is a two-dimensional geometric figure with opposite sides that are parallel and equal in length. The area of a parallelogram is the region it covers in a two-dimensional plane. The calculation of its area becomes particularly interesting when we have the lengths of its sides and the angle between these sides.
- Standard Area Formula: The standard formula for the area of a parallelogram is A = base × height. However, this requires knowledge of the height, which is not always readily available.
Calculating Area with Sides and Angle
When the height is not known, but the lengths of the sides and the angle between them are known, the area can be calculated using a trigonometric approach.
- Formula: The area can be calculated using the formula A = ab sin(θ), where \"a\" and \"b\" are the lengths of the adjacent sides of the parallelogram, and θ is the angle between these sides.
- Example: If the lengths of the sides are 8 cm and 9 cm, and the angle between them is 60 degrees, the area is calculated as follows: A = 8 × 9 × sin(60°) = 62.35 cm².
This method effectively utilizes the trigonometric function \"sine\" to calculate the area, making it a practical approach when the height of the parallelogram is not known.
Alternate Method: Using Diagonals
Another method to calculate the area of a parallelogram involves the lengths of its diagonals and the angle between them.
- Diagonal Formula: If the lengths of the diagonals d₁ and d₂ are known, and the angle y between them is given, the area can be calculated as A = ½ × d₁ × d₂ × sin(y).
This approach highlights the versatility of geometric principles in determining the area of parallelograms under different conditions, using the properties of sides, angles, and diagonals.

_HOOK_
Area Calculation Without Height
Calculating the area of a parallelogram without knowing its height requires a different approach, primarily involving trigonometry. This method is particularly useful when the height is not directly measurable or when working with the parallelogram\"s sides and angles instead.
- Basic Concept: The area of a parallelogram is traditionally calculated as the product of its base and height. However, when the height is not available, trigonometry provides an alternative.
- Using Sides and Angle: The formula for calculating the area in such cases is A = ab sin(θ), where \"a\" and \"b\" are the lengths of the parallelogram\"s adjacent sides, and θ is the angle between these sides.
- Example Calculation: If the lengths of the adjacent sides are 5 cm and 6 cm, and the angle between them is 30 degrees, the area is calculated as A = 5 × 6 × sin(30°) = 15 cm².
This method leverages the sine function to find the area, making it a practical solution when the height of the parallelogram is unknown or difficult to determine.
Alternative Method: Using Diagonals
Another approach to calculate the area without height involves the use of the parallelogram\"s diagonals.
- Formula: When the lengths of the diagonals (d₁ and d₂) and the angle (y) between them are known, the area can be calculated using A = ½ × d₁ × d₂ × sin(y).
- Example: For a parallelogram with diagonals of lengths 8 cm and 10 cm, intersecting at an angle of 45 degrees, the area is A = ½ × 8 × 10 × sin(45°) ≈ 28.28 cm².
These methods demonstrate the flexibility of geometric calculations, allowing for the determination of the area of a parallelogram in scenarios where the height is not readily available.

Advanced Perimeter Formulas
When calculating the perimeter of a parallelogram, advanced formulas can be used, especially when specific dimensions such as diagonals and angles are known. These methods extend beyond the basic formula of adding the lengths of all sides.
- Standard Formula: The basic formula for the perimeter of a parallelogram is P = 2(a + b), where \"a\" and \"b\" are the lengths of adjacent sides.
Perimeter Using Base, Height, and Angle
When the base, height, and an interior angle are known, the perimeter can be calculated using trigonometry.
- Formula: The formula for this scenario is P = 2(b + h/sin θ), where \"b\" is the base, \"h\" is the height, and θ is the angle between the base and height.
Perimeter Using Diagonals and a Side
This method involves using the lengths of the diagonals and one side of the parallelogram.
- Formula: The formula is P = 2a + √[2(x² + y² - 2a²)], where \"a\" is the length of a side, and \"x\" and \"y\" are the lengths of the diagonals.
- Example: For a parallelogram with one side measuring 5 units, and diagonals measuring 4 and 5 units, the perimeter would be calculated as follows: P = 2(5) + √[2(4² + 5² - 2(5)²)] = 30.94 units.
These advanced formulas allow for a more versatile approach to finding the perimeter of a parallelogram, especially in complex geometric problems where standard side measurements are not readily available.
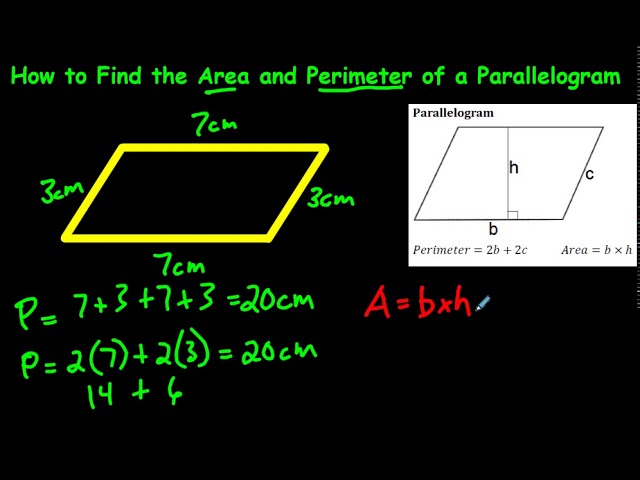
Practical Examples and Solved Problems
Understanding the concepts of area and perimeter of a parallelogram is best achieved through practical examples and solved problems. Here, we\"ll look at some typical problems that illustrate these concepts effectively.
Example 1: Calculating Perimeter with Given Sides
Consider a parallelogram with sides measuring 10 cm and 5 cm. To find its perimeter, we use the formula P = 2(a + b). In this case, P = 2(10 cm + 5 cm) = 2(15 cm) = 30 cm. Therefore, the perimeter of this parallelogram is 30 cm.
Example 2: Perimeter with Base, Height, and Angle
Imagine a parallelogram with a base of 17 cm, a height of 12 cm, and an interior angle of 60 degrees. The perimeter, in this case, can be calculated using P = 2(b + h/sin θ), resulting in P = 2(17 cm + 12 cm/sin 60°) ≈ 61.71 cm.
Example 3: Perimeter with One Side and Diagonals
For a parallelogram with one side measuring 7 units, and diagonals of 8 units and 10 units, the perimeter can be calculated using P = 2a + √[2(x² + y² - 2a²)]. Substituting the values, we get P = 2(7) + √[2(8² + 10² - 2(7)²)] ≈ 25.49 units.
Example 4: Area of a Parallelogram
Let\"s say we need to find the area of a parallelogram with a base of 9 feet and a height of 12 feet. Using the formula A = base x height, we get A = 9 ft x 12 ft = 108 ft².
These examples provide a clear demonstration of how to apply formulas for the perimeter and area of parallelograms in various scenarios, enhancing the understanding of these geometric concepts.
READ MORE:
FAQs and Common Misconceptions
The study of parallelograms often raises several questions and misconceptions. This section aims to address some of the most common queries and clarify misunderstandings related to the area and perimeter of parallelograms.
- What is the Perimeter of a Parallelogram?
- The perimeter of a parallelogram is the sum of the lengths of all its sides. For a parallelogram with adjacent sides of lengths \"a\" and \"b\", the perimeter is calculated as 2(a + b). This formula is based on the property that opposite sides of a parallelogram are equal in length.
- How is the Area of a Parallelogram Calculated?
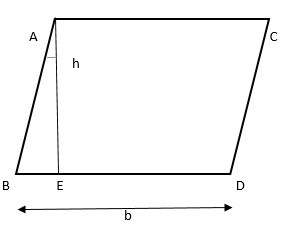
- The area of a parallelogram is determined by multiplying its base \"b\" by the height \"h\". The height is the perpendicular distance from the base to the opposite side. This formula stems from the fact that a parallelogram can be rearranged into a rectangle with the same base and height.
- Are Diagonals of a Parallelogram Equal?
- Contrary to a common misconception, the diagonals of a parallelogram are not necessarily equal. They bisect each other, but their lengths can vary. This characteristic helps distinguish parallelograms from other quadrilaterals like squares and rectangles.
- Can a Parallelogram Have Right Angles?
- Yes, a parallelogram can have right angles. If all angles in a parallelogram are right angles, it is also classified as a rectangle. However, not all parallelograms have right angles.
- Is Every Rectangle a Parallelogram?
- Yes, every rectangle is a parallelogram. This is because rectangles meet the definition of parallelograms - opposite sides are parallel and equal in length. However, not every parallelogram is a rectangle as parallelograms do not necessarily have right angles.
- Do the Sides of a Parallelogram Always Bisect Each Other at 90 Degrees?
- No, the diagonals of a parallelogram do not always bisect each other at 90 degrees. This is a common misconception. The diagonals bisect each other, but the angles formed at the intersection can vary.
Discover the intriguing world of parallelograms, where geometry meets practicality. Explore how the unique properties of parallelograms intertwine in everyday objects, from book covers to architectural designs, and unravel the fascinating calculations of their perimeters and areas. Join us on this geometric journey to appreciate the simplicity and complexity of parallelograms!