Topic perimeter and area of a triangle formula: Discover the essentials of geometry with our in-depth guide on the "Perimeter and Area of a Triangle Formula", unlocking the secrets of triangles for beginners and enthusiasts alike!
Table of Content
- What is the formula for finding the perimeter and area of a triangle?
- Basic Triangle Formulas
- Perimeter of Different Types of Triangles
- Area Calculation Methods
- Special Triangles: Equilateral, Isosceles, and Scalene
- Application of Heron\"s Formula
- Using Trigonometry in Area Calculation
- YOUTUBE: Finding the Area and Perimeter of a Triangle
- Examples and Practical Problems
- Tools and Calculators for Triangle Measurements
- Common Mistakes to Avoid in Calculations
- Real-world Applications of Triangle Formulas
What is the formula for finding the perimeter and area of a triangle?
The formulas for finding the perimeter and area of a triangle are as follows:
Perimeter:
- Add up the lengths of all three sides of the triangle to find the perimeter.
Area:
- There are multiple formulas to calculate the area of a triangle depending on the given information:
- Base and height:
- Measure the length of the base (b) of the triangle.
- Measure the perpendicular height (h) from the base to the opposite vertex.
- Apply the formula Area = (1/2) * base * height to find the area.
- Side lengths:
- If you know the lengths of all three sides of the triangle, you can use Heron\'s formula.
- Let a, b, and c represent the lengths of the triangle\'s sides.
- Calculate the semi-perimeter s using the formula s = (a + b + c) / 2.
- Use the formula Area = sqrt(s * (s - a) * (s - b) * (s - c)) to find the area.
Remember to use the appropriate formula based on the given information about the triangle.
READ MORE:
Basic Triangle Formulas
Understanding the basic formulas for the perimeter and area of a triangle is fundamental in geometry. The perimeter of a triangle is the sum of its three sides, denoted as P = a + b + c, where a, b, and c are the lengths of the sides. The area of a triangle can be calculated using different formulas depending on the available information.
- Standard Area Formula: For any triangle with base \"b\" and height \"h\", the area is given by A = ½ × b × h.
- Heron\"s Formula: When the lengths of all three sides are known, the area can be found using Heron\"s formula: A = √[s × (s - a) × (s - b) × (s - c)], where s is the semi-perimeter, s = ½ × (a + b + c).
- Trigonometric Method: In cases involving right triangles, or when angles and side lengths are known, trigonometric functions can be used. For a right triangle, A = ½ × base × height, and for other cases, A = ½ × a × b × Sin(C), where a and b are sides and C is the included angle.
Each of these methods offers a way to calculate the area and perimeter of triangles, making them versatile tools in geometry.

Perimeter of Different Types of Triangles
The perimeter of a triangle varies with its type. Each type of triangle—equilateral, isosceles, and scalene—has a unique way of calculating the perimeter.
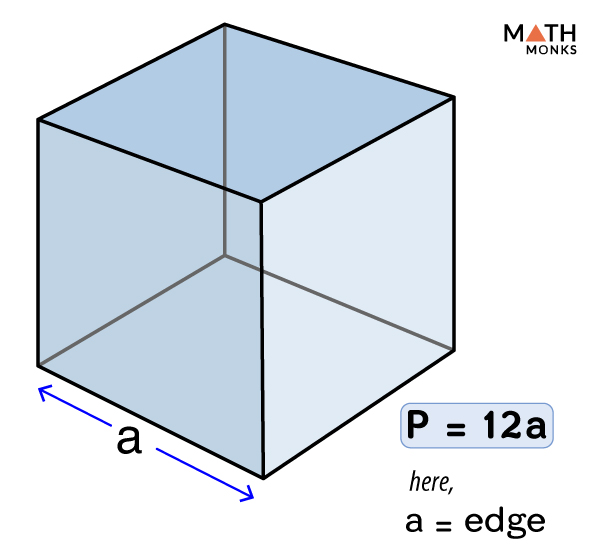
- Equilateral Triangle: In an equilateral triangle, all sides are equal in length. The perimeter is calculated as P = 3 × a, where \"a\" is the length of each side.
- Isosceles Triangle: An isosceles triangle has two equal sides. The perimeter is the sum of the lengths of the two equal sides plus the base, P = 2a + b, where \"a\" is the length of the equal sides and \"b\" is the base.
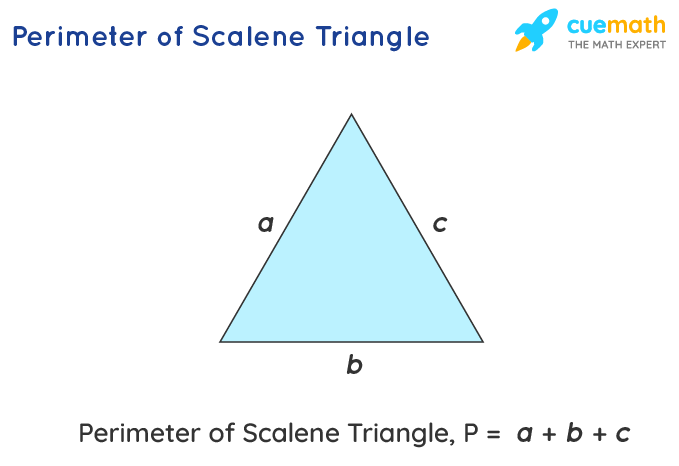
- Scalene Triangle: A scalene triangle has all sides of different lengths. The perimeter is simply the sum of these sides, P = a + b + c, where \"a\", \"b\", and \"c\" are the lengths of the sides.
Understanding these formulas helps in accurately determining the perimeter of various types of triangles, which is a fundamental aspect of geometry.

Area Calculation Methods
Calculating the area of a triangle can be done using various methods, each suited to different types of triangles and available measurements.
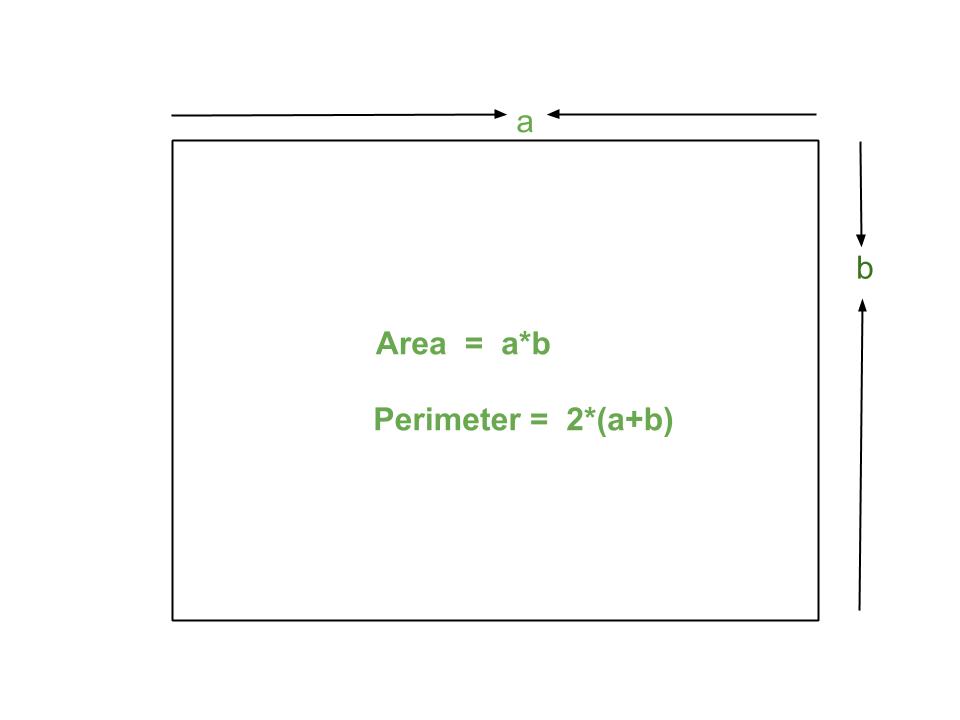
- Base and Height Method: The most common method involves using the formula A = ½ × b × h, where \"A\" is the area, \"b\" is the base, and \"h\" is the height perpendicular to the base.
- Heron\"s Formula: Useful when the lengths of all sides are known. Heron\"s formula is A = √[s × (s - a) × (s - b) × (s - c)], where \"s\" is the semi-perimeter, s = ½ × (a + b + c), and \"a\", \"b\", \"c\" are the side lengths.
- Trigonometric Methods: When angles are involved, the area can be calculated using A = ½ × a × b × Sin(C), where \"a\" and \"b\" are the lengths of two sides and \"C\" is the angle between them.
- Using Coordinates: If the triangle\"s vertices are known in a coordinate plane, the area can be found using the formula A = ½ |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|.
Each method provides a reliable way to calculate the area of triangles, making them crucial tools in both theoretical and applied mathematics.

Special Triangles: Equilateral, Isosceles, and Scalene
Calculating the area of a triangle can be done using various methods, each suited to different types of triangles and available measurements.
- Base and Height Method: The most common method involves using the formula A = ½ × b × h, where \"A\" is the area, \"b\" is the base, and \"h\" is the height perpendicular to the base.
- Heron\"s Formula: Useful when the lengths of all sides are known. Heron\"s formula is A = √[s × (s - a) × (s - b) × (s - c)], where \"s\" is the semi-perimeter, s = ½ × (a + b + c), and \"a\", \"b\", \"c\" are the side lengths.
- Trigonometric Methods: When angles are involved, the area can be calculated using A = ½ × a × b × Sin(C), where \"a\" and \"b\" are the lengths of two sides and \"C\" is the angle between them.
- Using Coordinates: If the triangle\"s vertices are known in a coordinate plane, the area can be found using the formula A = ½ |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|.
Each method provides a reliable way to calculate the area of triangles, making them crucial tools in both theoretical and applied mathematics.

_HOOK_
Application of Heron\"s Formula
Calculating the area of a triangle can be done using various methods, each suited to different types of triangles and available measurements.
- Base and Height Method: The most common method involves using the formula A = ½ × b × h, where \"A\" is the area, \"b\" is the base, and \"h\" is the height perpendicular to the base.
- Heron\"s Formula: Useful when the lengths of all sides are known. Heron\"s formula is A = √[s × (s - a) × (s - b) × (s - c)], where \"s\" is the semi-perimeter, s = ½ × (a + b + c), and \"a\", \"b\", \"c\" are the side lengths.
- Trigonometric Methods: When angles are involved, the area can be calculated using A = ½ × a × b × Sin(C), where \"a\" and \"b\" are the lengths of two sides and \"C\" is the angle between them.
- Using Coordinates: If the triangle\"s vertices are known in a coordinate plane, the area can be found using the formula A = ½ |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|.
Each method provides a reliable way to calculate the area of triangles, making them crucial tools in both theoretical and applied mathematics.

Using Trigonometry in Area Calculation
Trigonometry, a branch of mathematics that deals with triangles, particularly right triangles, can be used to calculate the area of a triangle in cases where the traditional base-times-height method is not applicable. This method is especially useful when the height of the triangle is not known or difficult to measure.
To calculate the area of a triangle using trigonometry, you need to know the lengths of two sides and the measure of the angle between them. This is often referred to as the SAS (Side-Angle-Side) method. The formula to calculate the area of a triangle using trigonometry is:
Area = ½ × a × b × sin(C)
where:
- a and b are the lengths of two sides of the triangle.
- C is the angle between sides a and b.
Steps for Calculating Area using Trigonometry:
- Measure the lengths of two sides of the triangle (a and b).
- Measure the angle (C) between these two sides.
- Use the formula: Area = ½ × a × b × sin(C) to calculate the area.
Example:
Suppose we have a triangle with two sides measuring 5 cm and 7 cm, and the angle between these sides is 30 degrees. To find the area:
- Plug the values into the formula: Area = ½ × 5 cm × 7 cm × sin(30°).
- Since sin(30°) = 0.5, the formula becomes: Area = ½ × 5 cm × 7 cm × 0.5.
- Calculate the area: Area = 8.75 cm².
It\"s important to note that this method is applicable only when you know two sides and the included angle. In the case of non-right triangles where this information is not available, other methods such as Heron\"s formula or using the heights can be employed.
Trigonometry provides a powerful tool for area calculation in triangles, especially in more complex geometric problems where traditional methods are not feasible. It offers a deeper understanding of the properties of triangles and their applications in various fields such as engineering, architecture, and astronomy.

Finding the Area and Perimeter of a Triangle
\"Discover the fascinating world of triangles in our enthralling video! From the Pythagorean theorem to trigonometry, we\'ll explore the beauty and practicality of these versatile shapes. Join us to unlock the secrets of triangles!\"
Calculating the Area and Perimeter of a Triangle
\"Unlock the power of calculation with our captivating video! Whether you\'re a math enthusiast or simply curious about numbers, we\'ve got you covered. Dive into the realm of equations, formulas, and problem-solving techniques. Join us on this journey to becoming a master calculator!\"
Examples and Practical Problems
Understanding the perimeter and area of triangles is not just a theoretical concept but also has practical applications in various fields. Below are examples and problems to demonstrate the practical application of these concepts.
Example 1: Calculating Perimeter of a Triangle
Consider a triangle with sides of lengths 7 cm, 5 cm, and 6 cm. To find the perimeter, simply add up the lengths of the sides.
Perimeter = 7 cm + 5 cm + 6 cm = 18 cm.
Example 2: Area Calculation of a Right-Angled Triangle
For a right-angled triangle with a base of 8 cm and height of 6 cm, the area is calculated using the formula: Area = 1/2 × base × height.
Area = 1/2 × 8 cm × 6 cm = 24 cm2.
Example 3: Using Heron\"s Formula
For a scalene triangle with sides 8 cm, 6 cm, and 7 cm, first calculate the semi-perimeter (s = (a + b + c) / 2).
Semi-perimeter, s = (8 cm + 6 cm + 7 cm) / 2 = 10.5 cm.
Area = √[s × (s - a) × (s - b) × (s - c)] = √[10.5 × (10.5 - 8) × (10.5 - 6) × (10.5 - 7)] cm2.
Practice Problems
- Find the perimeter of a triangle with sides measuring 3 cm, 4 cm, and 5 cm.
- Calculate the area of an equilateral triangle with a side of 5 cm.
- Using Heron\"s formula, find the area of a triangle with sides of 9 cm, 10 cm, and 11 cm.
- Find the height of a triangle given its base is 12 cm and area is 36 cm2.
These examples and problems illustrate the practical application of the formulas for perimeter and area of triangles. Understanding these concepts is crucial for solving real-world problems in geometry and related fields.

Tools and Calculators for Triangle Measurements
In the field of geometry, accurately measuring the perimeter and area of triangles is crucial. This section introduces various tools and calculators that can assist in these measurements, ensuring precision and ease in calculations.
Online Calculators
- Perimeter Calculator: Allows input of the three side lengths to calculate the perimeter of any triangle.
- Area Calculator using Base and Height: Calculates the area of a triangle when the base and height are known.
- Area Calculator using Heron\"s Formula: Ideal for scalene triangles where all sides are of different lengths.
- Area Calculator for Right-Angled Triangles: Specifically designed for calculating the area of right-angled triangles.
- Specialized Calculators for Equilateral and Isosceles Triangles: These calculators use specific formulas tailored for equilateral and isosceles triangles.
Mobile Applications
Several mobile apps are available that offer interactive ways to calculate triangle measurements. These apps often include visual aids and can be particularly helpful for educational purposes.
Geometric Tools
Traditional geometric tools like rulers, protractors, and compasses are indispensable for manual measurements and understanding the basics of triangle geometry.
Software Programs
Certain software programs offer advanced features such as 3D modeling and can calculate areas and perimeters of triangles in complex diagrams.
Whether you prefer online calculators, mobile apps, traditional tools, or software programs, there is a wide range of options available for measuring the perimeter and area of triangles. These tools can significantly aid in both educational and professional geometric calculations.
Common Mistakes to Avoid in Calculations
When calculating the perimeter and area of triangles, it\"s crucial to be aware of common mistakes to ensure accurate results. This section outlines typical errors and provides guidance on how to avoid them.
Mistake 1: Incorrect Formula Application
Applying the wrong formula for different types of triangles is a frequent error. Remember:
- For an equilateral triangle (all sides equal), use Perimeter = 3a and Area = (√3/4) × side².
- For an isosceles triangle (two sides equal), use Perimeter = 2s + b and Area = 1/2 × Base × Height.
- For a scalene triangle (all sides different), use Perimeter = a + b + c and Heron\"s formula for the area.
Mistake 2: Miscalculating Semi-Perimeter in Heron\"s Formula
When using Heron\"s formula for a scalene triangle, accurately calculate the semi-perimeter: s = (a + b + c)/2. An error in this step leads to incorrect area calculation.
Mistake 3: Confusing Units
Ensure that all measurements are in the same unit before calculating. Mixing different units (like cm and inches) will result in inaccurate calculations.
Mistake 4: Incorrect Height Measurement
For area calculations, height must be perpendicular to the base. Measuring at an angle leads to errors.
Mistake 5: Overlooking the Triangle Type
Different triangle types require different formulas. Ensure that you identify the triangle type correctly before proceeding with calculations.
By understanding and avoiding these common mistakes, you can ensure more accurate results in your calculations of triangle perimeters and areas.
_HOOK_
READ MORE:
Real-world Applications of Triangle Formulas
Triangle formulas for perimeter and area are not just theoretical concepts but have numerous practical applications in various fields. Understanding these applications highlights the importance of accurate calculation in real-world scenarios.
Application 1: Architecture and Construction
In architecture and construction, the area and perimeter of triangles play a crucial role in designing roofs, trusses, and bridges. Accurate calculations ensure structural integrity and efficient use of materials.
Application 2: Land Surveying
Land surveyors often use triangle formulas to calculate the size and boundaries of plots. This is especially useful in areas with irregular shapes, where triangles are used to approximate the land\"s dimensions.
Application 3: Navigation and Mapping
Triangle formulas are employed in navigation and mapping to determine distances and plot courses, particularly in aviation and maritime navigation where triangulation is a common technique.
Application 4: Computer Graphics
In computer graphics, triangles are fundamental in rendering 3D models. Calculating the area and perimeter of triangles helps in creating realistic textures and shadows.
Application 5: Science and Engineering
Various branches of science and engineering use triangle formulas for structural analysis, calculating forces, and in the study of molecular structures and crystal lattices.
These real-world applications of triangle formulas demonstrate their versatility and importance across multiple disciplines, emphasizing the practical value of understanding geometric principles.
Mastering the formulas for the perimeter and area of a triangle opens doors to a world of practical applications, from architectural designs to technological advancements. Delve into this comprehensive guide to unlock the secrets of these fundamental geometric concepts and enhance your understanding of their versatile role in everyday life.