Topic square root how to find: Discover the most effective methods to find the square root of any number, whether it's a perfect or imperfect square. This comprehensive guide provides clear explanations and step-by-step instructions to help you master the concept of square roots and apply them confidently in mathematical problems.
Understanding the definition and basic properties of square roots. This section explains the fundamental relationship between squares and square roots.
Steps to find the square root of perfect squares using prime factorization.
Detailed process of finding square roots for both perfect and non-perfect squares using the long division method.
Examples of finding the square roots of numbers like 81, 625, etc., using various methods.
Explanation and examples of finding square roots of non-perfect squares such as 2, 3, and 5 using the long division method.
Methods to find square roots of decimal numbers using both prime factorization and long division methods. Examples included.
Explanation of how to deal with the square roots of negative numbers, introducing the concept of imaginary numbers.
Various practical examples and applications of square roots in solving mathematical equations and real-world problems.
Links to video tutorials and additional reading materials for further learning and practice.
Table of Content
How to Find the Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9. There are various methods to find the square root of a number, including prime factorization, long division, and using a calculator.
Methods to Find the Square Root
Prime Factorization Method
This method is useful for perfect squares. Here are the steps:
- Factorize the number into its prime factors.
- Pair the prime factors.
- The product of one number from each pair gives the square root.
Example:
- Square root of 81: 81 = 3 × 3 × 3 × 3, paired as (3×3) and (3×3), thus √81 = 3 × 3 = 9.
- Square root of 625: 625 = 5 × 5 × 5 × 5, paired as (5×5) and (5×5), thus √625 = 5 × 5 = 25.
Long Division Method
This method is used for both perfect and non-perfect squares. Here are the steps:
- Group the digits in pairs from right to left for the integer part and left to right for the decimal part.
- Find the largest number whose square is less than or equal to the first group. This is the first digit of the square root.
- Subtract the square of this digit from the first group and bring down the next pair of digits.
- Double the current quotient and determine the next digit which, when appended to the divisor and multiplied by the new digit, gives a product less than or equal to the current number.
- Repeat until you reach the desired precision.
Example:
- Square root of 7921 by long division is 89.
- Square root of 2 by long division is approximately 1.4142.
Using a Calculator
The simplest method to find the square root of any number is by using a calculator. Most calculators have a square root function, denoted as √.
Square Roots of Decimal Numbers
To find the square root of a decimal number, the same methods can be applied:
- Prime factorization method by expressing the decimal as a fraction.
- Long division method by considering pairs of digits in the decimal part.
Example:
- Square root of 6.25 is 2.5 because 6.25 = 625/100 and √625/100 = 25/10 = 2.5.
- Square root of 42.25 by long division is 6.5.
Perfect Squares
Perfect squares are numbers that are the square of an integer. Here are some examples:
- 4 (2×2)
- 9 (3×3)
- 16 (4×4)
- 25 (5×5)
- 36 (6×6)
- 49 (7×7)
- 64 (8×8)
- 81 (9×9)
- 100 (10×10)
Square Root Symbol
The square root symbol is √. For example, √25 = 5.

READ MORE:
Introduction
Finding the square root of a number is an essential mathematical skill that can be applied in various fields such as engineering, physics, and everyday problem-solving. This guide will introduce you to different methods to find square roots, making it easier to understand and compute them. We'll explore the following:
- Basic Concept of Square Roots
- Prime Factorization Method
- Long Division Method
- Square Roots of Perfect Squares
- Square Roots of Imperfect Squares
- Square Roots of Decimal Numbers
- Special Cases: Negative and Imaginary Numbers
- Applications and Examples
By mastering these techniques, you'll be able to solve mathematical problems more efficiently and with greater confidence.
Basic Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented by the radical symbol √. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Here are the basic properties of square roots:
- The square root of a positive number is always positive.
- The square root of zero is zero.
- There are no real square roots of negative numbers; these involve imaginary numbers.
Mathematically, the square root of a number x is represented as:
\[\sqrt{x}\]
To find the square root of a number, follow these steps:
- Identify Perfect Squares: Determine if the number is a perfect square. For example, 1, 4, 9, 16, and 25 are perfect squares because they are squares of 1, 2, 3, 4, and 5, respectively.
- Prime Factorization: For perfect squares, express the number as a product of prime factors. For example, 36 can be written as \(2^2 \times 3^2\).
- Long Division Method: For non-perfect squares, use the long division method to find the square root. This involves dividing the number into pairs of digits, estimating the largest possible digits, and performing a series of subtractions and divisions.
Understanding these basic concepts is crucial before moving on to more advanced methods of finding square roots.
Methods to Find Square Root
There are several methods to find the square root of a number, each suitable for different types of numbers and precision requirements. Below, we will explore three common methods: the Prime Factorization Method, the Long Division Method, and the Estimation Method.
1. Prime Factorization Method
This method is effective for finding the square roots of perfect squares. Follow these steps:
- Factorize the Number: Break down the number into its prime factors. For example, for 144, the prime factorization is \(144 = 2^4 \times 3^2\).
- Pair the Factors: Group the prime factors into pairs of identical numbers. Using the example above, \(144 = (2^2) \times (2^2) \times (3^2)\).
- Take One Factor from Each Pair: Take one number from each pair and multiply them together. For \(144 = (2 \times 2 \times 3) = 12\), so \(\sqrt{144} = 12\).
2. Long Division Method
This method can be used for both perfect and non-perfect squares. Here are the steps:
- Separate the Digits into Pairs: Start from the decimal point and move left and right, grouping digits in pairs. For example, for 152.2756, group as (1)(52.)(27)(56).
- Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair or single digit. In this case, \(1^2 = 1\).
- Subtract and Bring Down the Next Pair: Subtract the square of the integer found from the first pair, and bring down the next pair of digits. Repeat the process.
- Form a New Divisor: Double the number found so far, and determine a digit to complete the divisor that allows for the new subtraction to be as close to zero as possible without going negative.
3. Estimation Method
This method provides an approximate value of the square root and is useful for quick calculations:
- Identify Perfect Squares: Find the two closest perfect squares between which the number lies. For example, for 20, it lies between 16 (\(4^2\)) and 25 (\(5^2\)).
- Estimate the Value: Estimate a value between the two perfect squares. For 20, the square root would be between 4 and 5. A closer estimate would be 4.5 or refined further as needed.
By understanding and practicing these methods, you can effectively find the square roots of various numbers with ease and accuracy.
Square Roots of Perfect Squares
Perfect squares are numbers that are the square of an integer. Finding the square roots of perfect squares is straightforward because they have exact integer values. Here are detailed steps to find the square roots of perfect squares using two common methods: Prime Factorization and Direct Calculation.
1. Prime Factorization Method
To find the square root of a perfect square using prime factorization, follow these steps:
- Factorize the Number: Break down the number into its prime factors. For example, consider 144:
- 144 can be factorized as \(144 = 2^4 \times 3^2\).
- Pair the Factors: Group the prime factors into pairs of identical numbers:
- For 144: \(144 = (2^2) \times (2^2) \times (3^2)\).
- Take One Factor from Each Pair: Take one number from each pair and multiply them together:
- \(\sqrt{144} = 2 \times 2 \times 3 = 12\).
2. Direct Calculation Method
This method involves recognizing the number as a square of an integer directly:
- Identify the Perfect Square: Recognize the number as a square of an integer. For example, 81 is a perfect square because \(9 \times 9 = 81\).
- Calculate the Square Root: Determine the integer that, when multiplied by itself, gives the original number:
- \(\sqrt{81} = 9\) because \(9^2 = 81\).
Examples
Let's look at some examples to solidify our understanding:
| Number | Prime Factorization | Square Root |
|---|---|---|
| 49 | \(7^2\) | 7 |
| 100 | \(2^2 \times 5^2\) | 10 |
| 225 | \(3^2 \times 5^2\) | 15 |
By understanding and applying these methods, you can efficiently find the square roots of perfect squares, ensuring accuracy and confidence in your calculations.
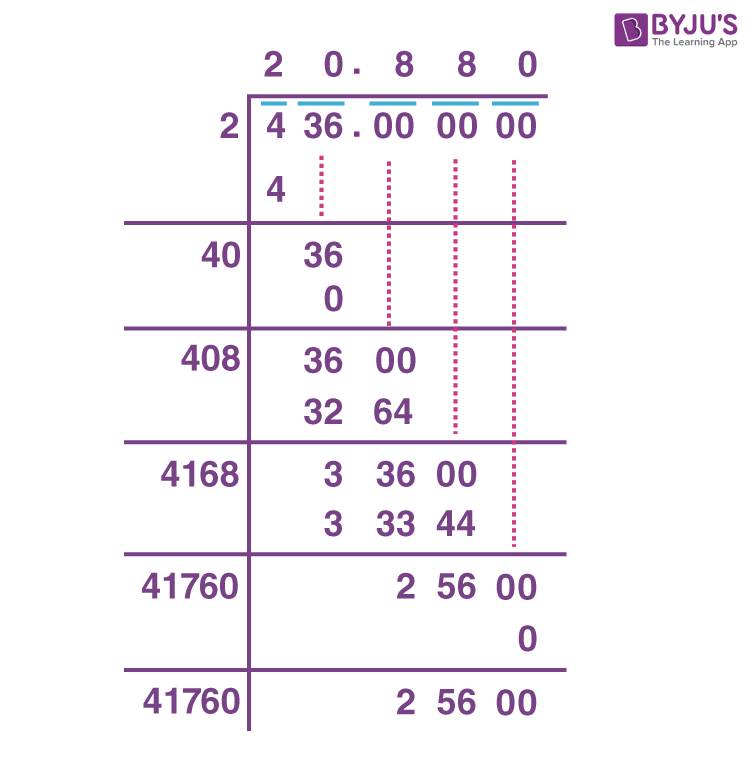
Square Roots of Imperfect Squares
Imperfect squares are numbers that do not have exact integer square roots. Finding the square roots of imperfect squares requires methods that provide approximate values. The most common method used is the Long Division Method. Below are the detailed steps to find the square root of imperfect squares:
Long Division Method
This method allows you to find the square root of any number with a high degree of accuracy. Here’s how to do it:
- Separate the Digits into Pairs: Start from the decimal point and move left and right, grouping digits in pairs. For example, for 152.2756, group as (1)(52.)(27)(56).
- Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair or single digit. For 1, the largest integer is 1 because \(1^2 = 1\).
- Subtract and Bring Down the Next Pair: Subtract the square of the integer found from the first pair, and bring down the next pair of digits. For example, \(1 - 1 = 0\), bring down 52 to get 052.
- Form a New Divisor: Double the number found so far (1 becomes 2), and determine a digit (x) to complete the divisor (20x) that allows for the new subtraction to be as close to zero as possible without going negative. In this case, \(22 \times 2 = 44\), leaving a remainder of 8.
- Repeat the Process: Bring down the next pair of digits (27), making it 827. Continue the process of finding the next digit (x) to complete the new divisor (40x + x) and performing the subtraction. Repeat until you reach the desired level of accuracy.
Example: Finding \(\sqrt{20}\)
Using the long division method to find the square root of 20:
- Pair the Digits: (20.00)
- First Approximation: The largest integer whose square is less than or equal to 20 is 4 (since \(4^2 = 16\)).
- Subtract and Bring Down: \(20 - 16 = 4\), bring down 00 to get 400.
- Form New Divisor: Double 4 to get 8. Find x such that \(80x \times x\) is less than or equal to 400. The digit is 4 (since \(84 \times 4 = 336\)).
- Continue Process: \(400 - 336 = 64\), bring down 00 to get 6400. Next divisor is 880, and repeat the process.
By following these steps, you can find the square roots of imperfect squares accurately. This method is useful for calculating square roots by hand or understanding the principles behind square root algorithms used in calculators.
Special Cases: Negative and Imaginary Numbers
Square roots of negative numbers do not exist within the set of real numbers because a square of any real number is always non-negative. To address the square roots of negative numbers, we introduce the concept of imaginary numbers. Here’s a detailed explanation:
Understanding Imaginary Numbers
Imaginary numbers are based on the imaginary unit \(i\), which is defined as the square root of -1. Therefore:
\[i = \sqrt{-1}\]
Using this definition, the square root of any negative number can be expressed in terms of \(i\). For example:
- The square root of -4 is \(\sqrt{-4} = \sqrt{4 \times -1} = 2i\).
- The square root of -9 is \(\sqrt{-9} = \sqrt{9 \times -1} = 3i\).
Finding the Square Root of a Negative Number
To find the square root of a negative number, follow these steps:
- Factorize the Number: Separate the number into its positive part and the negative unit. For example, -25 can be written as \(25 \times -1\).
- Find the Square Root of the Positive Part: Calculate the square root of the positive part. For \(25\), the square root is 5.
- Multiply by \(i\): Multiply the result by \(i\) to incorporate the square root of the negative unit. For \(\sqrt{25 \times -1}\), this results in \(5i\).
Examples
Let’s look at a few examples to better understand the process:
| Number | Calculation | Square Root |
|---|---|---|
| -16 | \(\sqrt{-16} = \sqrt{16 \times -1} = 4i\) | 4i |
| -49 | \(\sqrt{-49} = \sqrt{49 \times -1} = 7i\) | 7i |
| -64 | \(\sqrt{-64} = \sqrt{64 \times -1} = 8i\) | 8i |
By understanding these special cases, you can extend your knowledge of square roots to include negative numbers, using the concept of imaginary numbers to provide meaningful solutions.
Applications and Examples
The concept of square roots is widely used in various fields such as mathematics, science, engineering, and everyday life. Below are some detailed applications and examples of how square roots are utilized:
Mathematical Applications
Square roots play a crucial role in solving quadratic equations, understanding geometric shapes, and working with exponents and logarithms.
- Quadratic Equations: To find the roots of the quadratic equation \(ax^2 + bx + c = 0\), the quadratic formula \(\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) involves calculating the square root of the discriminant (\(b^2 - 4ac\)).
- Pythagorean Theorem: In geometry, the square root is used to find the length of the hypotenuse of a right-angled triangle. For a triangle with legs \(a\) and \(b\), the hypotenuse \(c\) is found using \(c = \sqrt{a^2 + b^2}\).
- Exponents and Logarithms: Square roots are a specific case of fractional exponents. For example, \(\sqrt{x} = x^{1/2}\).
Scientific Applications
In science, square roots are used in various calculations involving physical laws and statistical measures.
- Physics: The formula for calculating the period of a pendulum \(T = 2\pi\sqrt{\frac{L}{g}}\) involves the square root of the ratio of the length of the pendulum (\(L\)) to the acceleration due to gravity (\(g\)).
- Statistics: The standard deviation, which measures the amount of variation or dispersion in a set of values, is calculated using the square root of the variance.
Engineering Applications
In engineering, square roots are used in structural design, signal processing, and many other areas.
- Structural Design: Engineers use square roots to calculate stress and strain in materials, ensuring structures can withstand forces and loads.
- Signal Processing: The Root Mean Square (RMS) value is used to represent the magnitude of a varying signal, such as in electrical engineering for AC voltage and current calculations.
Everyday Life Examples
Square roots are also applicable in various everyday scenarios:
- Financial Calculations: In finance, the square root is used to calculate compound interest rates and in various financial models to assess risk and return.
- Computer Graphics: In computer graphics, algorithms for rendering images often use square roots for distance calculations and transformations.
Examples
| Application | Formula | Example |
|---|---|---|
| Quadratic Equation | \(\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) | For \(x^2 - 4x + 4 = 0\), roots are \(x = \frac{4 \pm \sqrt{16 - 16}}{2} = 2\). |
| Pythagorean Theorem | \(c = \sqrt{a^2 + b^2}\) | For a triangle with \(a = 3\) and \(b = 4\), \(c = \sqrt{9 + 16} = 5\). |
| Standard Deviation | \(\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}\) | For data set \{2, 4, 4, 4, 5, 5, 7, 9\}, \(\sigma = 2\). |
By understanding these applications and examples, you can appreciate the importance of square roots in various domains and their practical significance in solving real-world problems.
Video Lessons and Additional Resources
To enhance your understanding of finding square roots, here are some valuable video lessons and additional resources:
-
Khan Academy:
- - A detailed video on simplifying square roots using various methods.
- - Learn about the properties and graphs of square root functions.
- - A comprehensive introduction to radical functions and their applications.
-
Math is Fun:
- - A detailed explanation of square roots, including perfect and imperfect squares, and step-by-step methods for finding them.
-
Virtual Nerd:
- - An interactive tutorial on finding square roots of perfect squares.
- - A step-by-step guide to finding square roots of non-perfect squares.
These resources provide a mix of video tutorials and written guides to help you master the concept of square roots. Whether you're dealing with perfect squares, non-perfect squares, or decimal numbers, these lessons will offer comprehensive support and practice opportunities.

Square Root: How to Find
READ MORE:
Cách Tính Căn Bậc Hai - Những Con Số Thay Đổi Toán Học Mãi Mãi