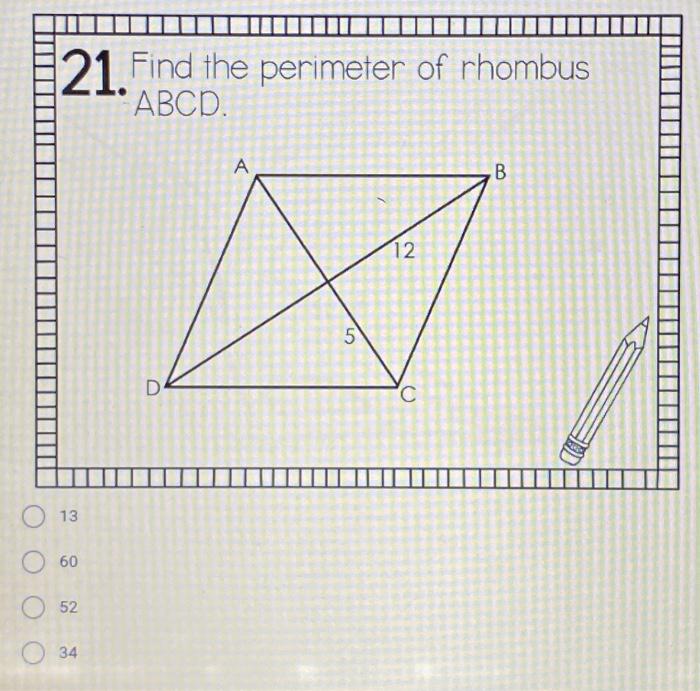
Topic perimeter of rhombus formula: Discover how to calculate the perimeter of a rhombus effortlessly with our comprehensive guide. Learn the fundamental formula, explore different methods, and understand practical applications. Whether you are a student or a math enthusiast, this article will provide you with the essential knowledge to master the perimeter of a rhombus.
Table of Content
- Perimeter of a Rhombus Formula
- Introduction to Rhombus
- Definition and Properties of a Rhombus
- Understanding the Perimeter of a Rhombus
- Basic Formula for Calculating Perimeter
- Steps to Calculate the Perimeter of a Rhombus
- Examples of Perimeter Calculation
- Alternative Methods for Finding Perimeter
- Using Diagonals to Determine Perimeter
- Application of the Pythagorean Theorem
- Common Mistakes to Avoid
- Practical Applications of Rhombus Perimeter
- Conclusion and Summary
- YOUTUBE: Hướng dẫn cách tính chu vi hình thoi một cách chi tiết và dễ hiểu. Video này phù hợp cho những ai đang tìm hiểu về công thức chu vi hình thoi.
Perimeter of a Rhombus Formula
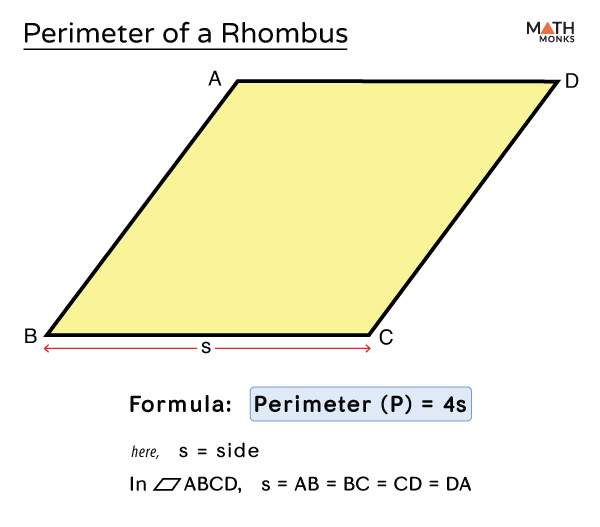
The perimeter of a rhombus is the total distance around the outside of the rhombus. It is a simple calculation based on the length of its sides.
Formula
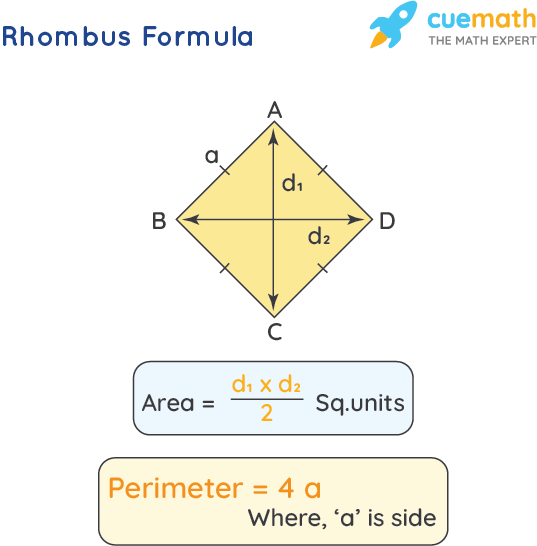
The perimeter \( P \) of a rhombus can be calculated using the formula:
\[ P = 4a \]
where \( a \) is the length of one side of the rhombus.
Steps to Calculate the Perimeter
- Measure the length of one side of the rhombus.
- Multiply the length by 4.
Example
For a rhombus with a side length of 5 units, the perimeter is calculated as:
\[ P = 4 \times 5 = 20 \, \text{units} \]
Using Diagonals to Calculate the Perimeter
If the lengths of the diagonals are known, the perimeter can also be calculated using the Pythagorean theorem. The diagonals of a rhombus bisect each other at right angles, forming four right-angled triangles.
The formula to find the side length \( a \) using the diagonals \( d_1 \) and \( d_2 \) is:
\[ a = \sqrt{\left( \frac{d_1}{2} \right)^2 + \left( \frac{d_2}{2} \right)^2} \]
Once the side length \( a \) is found, the perimeter can be calculated using the primary formula \( P = 4a \).
Example Using Diagonals
For a rhombus with diagonals of lengths 6 units and 8 units:
\[ a = \sqrt{\left( \frac{6}{2} \right)^2 + \left( \frac{8}{2} \right)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{units} \]
Then, the perimeter is:
\[ P = 4 \times 5 = 20 \, \text{units} \]
READ MORE:
Introduction to Rhombus
A rhombus is a special type of quadrilateral that is also known as an equilateral quadrilateral because all four of its sides are of equal length. This shape is a type of parallelogram with opposite sides that are parallel and opposite angles that are equal. The diagonals of a rhombus intersect each other at right angles, creating four congruent right triangles. Understanding the properties and characteristics of a rhombus is essential for various geometric calculations, including finding its perimeter and area.
- Equal Sides: All four sides of a rhombus are of equal length.
- Parallel Sides: Opposite sides are parallel.
- Equal Angles: Opposite angles are equal.
- Diagonal Properties: The diagonals of a rhombus bisect each other at right angles and divide the rhombus into four congruent right triangles.
These properties make the rhombus a unique and interesting shape in geometry, commonly used in various applications and problems involving distance, angles, and symmetry.
Definition and Properties of a Rhombus
A rhombus is a type of quadrilateral where all four sides have equal length. It is a special type of parallelogram, meaning it has two pairs of parallel sides. The defining characteristics and properties of a rhombus are as follows:
- All sides are of equal length.
- Opposite sides are parallel.
- Opposite angles are equal.
- Adjacent angles are supplementary (sum up to 180 degrees).
- The diagonals of a rhombus bisect each other at right angles (90 degrees).
- Each diagonal divides the rhombus into two congruent triangles.
Mathematically, if the side length of a rhombus is denoted as \( s \), the perimeter \( P \) of the rhombus can be calculated using the formula:
\[ P = 4s \]
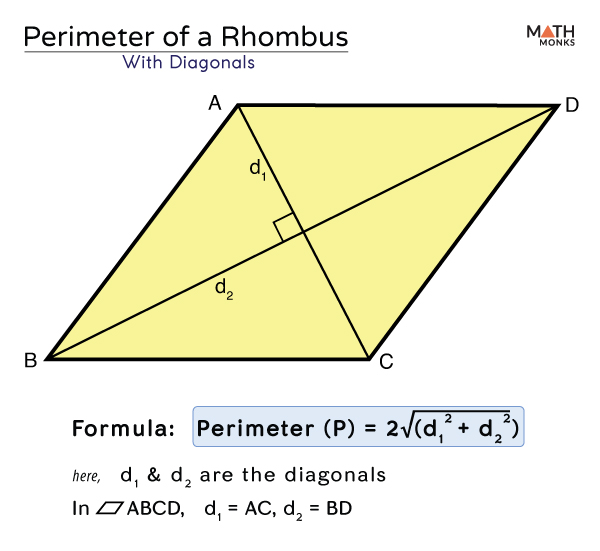
If the lengths of the diagonals are known, say \( d_1 \) and \( d_2 \), the perimeter can also be calculated using the formula:
\[ P = 2\sqrt{d_1^2 + d_2^2} \]
These properties make the rhombus a unique and interesting geometric shape with various applications in mathematics and real life.
Understanding the Perimeter of a Rhombus
A rhombus is a special type of parallelogram where all four sides are of equal length. The perimeter of a rhombus is the total distance around its edges. Since all sides are equal, the formula for the perimeter \( P \) is straightforward and can be expressed as:
\[ P = 4s \]
where \( s \) represents the length of one side. Let's break down the steps to understand this formula:
-
Measure the length of one side of the rhombus. Because all sides are equal, this measurement is sufficient to calculate the perimeter.
-
Multiply the length of one side by four. This is because a rhombus has four equal sides, and summing their lengths gives the total perimeter.
In summary, the perimeter of a rhombus is simply four times the length of one of its sides, making it easy to calculate once you have the side length.
Basic Formula for Calculating Perimeter
The perimeter of a rhombus is the total distance around the shape. Since all four sides of a rhombus are of equal length, calculating the perimeter is straightforward. The formula for the perimeter \( P \) of a rhombus with side length \( s \) is:
\[
P = 4s
\]
Where \( s \) represents the length of one side of the rhombus. This simple formula allows you to quickly determine the perimeter as long as you know the side length.
Steps to Calculate the Perimeter of a Rhombus
Calculating the perimeter of a rhombus involves a straightforward process using the length of one of its sides. Here are the steps to follow:
- Identify the length of one side: A rhombus has four sides of equal length. Measure or identify the length of one of the sides, denoted as s.
- Use the perimeter formula: The formula for the perimeter (P) of a rhombus is given by: \[ P = 4s \]
- Calculate the perimeter: Multiply the length of one side by 4 to get the perimeter. For example, if the side length is 5 cm, the calculation would be: \[ P = 4 \times 5 = 20 \, \text{cm} \]
By following these steps, you can easily determine the perimeter of any rhombus.
Examples of Perimeter Calculation
Calculating the perimeter of a rhombus is straightforward when you know the length of its sides. The formula for the perimeter is:
\(\text{Perimeter} = 4 \times a\)
where \(a\) is the length of a side of the rhombus.
Let's look at a couple of examples to understand this better:
- Example 1:
- Suppose each side of the rhombus is 5 cm.
- Using the formula, \(\text{Perimeter} = 4 \times 5\).
- So, the perimeter is \(20\) cm.
- Example 2:
- If the side length of a rhombus is 7 m,
- The perimeter is calculated as \(4 \times 7\).
- Thus, the perimeter is \(28\) m.
When the diagonals of a rhombus are given, the side length can be calculated using the Pythagorean theorem, as the diagonals bisect each other at right angles.
- Example 3:
- Given diagonals \(d_1 = 6\) cm and \(d_2 = 8\) cm,
- The side length \(a\) is calculated as \(\sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2}\).
- So, \(a = \sqrt{(3)^2 + (4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) cm.
- Thus, the perimeter is \(4 \times 5 = 20\) cm.
Alternative Methods for Finding Perimeter
There are several alternative methods to find the perimeter of a rhombus apart from the basic formula of multiplying the side length by 4. Below are some of the methods explained in detail:
Using Diagonals
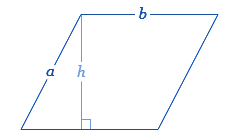
One of the alternative methods to find the perimeter of a rhombus is by using the lengths of its diagonals. The diagonals of a rhombus bisect each other at right angles. Given the lengths of the diagonals, we can use the Pythagorean theorem to find the side length, and then calculate the perimeter.
- Let \(d_1\) and \(d_2\) be the lengths of the diagonals.
- The side length \(a\) of the rhombus can be found using the formula: \[ a = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2} \]
- Once the side length \(a\) is determined, the perimeter \(P\) is: \[ P = 4a \]
Using Trigonometry
If the angle between two adjacent sides of the rhombus is known, trigonometric identities can be used to find the perimeter.
- Let \(a\) be the side length and \(\theta\) be the measure of one of the angles.
- If the side length \(a\) and angle \(\theta\) are known, the perimeter \(P\) can be calculated directly as: \[ P = 4a \]
- If only the diagonals \(d_1\) and \(d_2\) are known, first find the side length \(a\) using: \[ a = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2} \]
- Then, the perimeter \(P\) is: \[ P = 4a \]
Using Coordinates
When the vertices of the rhombus are given in coordinate form, the distance formula can be used to find the side lengths and then the perimeter.
- Let the vertices of the rhombus be \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\), and \((x_4, y_4)\).
- Calculate the length of one side using the distance formula: \[ a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Once the side length \(a\) is found, the perimeter \(P\) is: \[ P = 4a \]
These alternative methods provide flexibility in calculating the perimeter of a rhombus depending on the given information.
Using Diagonals to Determine Perimeter
One alternative method to find the perimeter of a rhombus is by using its diagonals. The diagonals of a rhombus intersect at right angles and bisect each other, creating four right-angled triangles. This relationship allows us to apply the Pythagorean theorem to find the length of a side, and subsequently the perimeter.
The formula to determine the perimeter of a rhombus using its diagonals \(d_1\) and \(d_2\) is:
\( P = 2 \sqrt{d_1^2 + d_2^2} \)
Here's a step-by-step process to find the perimeter using the diagonals:
- Measure the lengths of the diagonals \(d_1\) and \(d_2\).
- Square each of the diagonal lengths: \(d_1^2\) and \(d_2^2\).
- Add the squares of the diagonals: \(d_1^2 + d_2^2\).
- Take the square root of the sum: \(\sqrt{d_1^2 + d_2^2}\).
- Multiply the result by 2 to get the perimeter: \(P = 2 \sqrt{d_1^2 + d_2^2}\).
For example, let's calculate the perimeter of a rhombus with diagonals 8 cm and 12 cm:
- \(d_1 = 8\) cm and \(d_2 = 12\) cm
- \(d_1^2 = 8^2 = 64\) and \(d_2^2 = 12^2 = 144\)
- \(64 + 144 = 208\)
- \(\sqrt{208} \approx 14.42\)
- \(P = 2 \times 14.42 \approx 28.84\) cm
Therefore, the perimeter of the rhombus is approximately 28.84 cm.

Application of the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that can be applied to find the perimeter of a rhombus when the lengths of its diagonals are known. Here is a detailed, step-by-step explanation of how to use this theorem:
- Identify the Lengths of the Diagonals
Let the lengths of the diagonals of the rhombus be \( d_1 \) and \( d_2 \).
- Divide the Diagonals
Each diagonal bisects the rhombus into two right triangles. Therefore, each half of the diagonals is \( \frac{d_1}{2} \) and \( \frac{d_2}{2} \).
- Apply the Pythagorean Theorem
To find the side length \( s \) of the rhombus, use the Pythagorean Theorem in one of the right triangles formed by the diagonals:
\[
s = \sqrt{\left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2}
\] - Calculate the Side Length
Perform the calculations to find \( s \):
\[
s = \sqrt{\frac{d_1^2}{4} + \frac{d_2^2}{4}} = \frac{\sqrt{d_1^2 + d_2^2}}{2}
\] - Determine the Perimeter
The perimeter \( P \) of the rhombus is four times the side length \( s \):
\[
P = 4s = 4 \times \frac{\sqrt{d_1^2 + d_2^2}}{2} = 2\sqrt{d_1^2 + d_2^2}
\]
Here is an example to illustrate the process:
- Example: Find the perimeter of a rhombus with diagonals of 12 cm and 16 cm.
- Identify the diagonals: \( d_1 = 12 \) cm and \( d_2 = 16 \) cm.
- Apply the Pythagorean Theorem: \[ s = \frac{\sqrt{12^2 + 16^2}}{2} = \frac{\sqrt{144 + 256}}{2} = \frac{\sqrt{400}}{2} = 10 \text{ cm} \]
- Calculate the perimeter: \[ P = 4s = 4 \times 10 = 40 \text{ cm} \]
Thus, by using the Pythagorean Theorem, we can efficiently determine the perimeter of a rhombus when the lengths of its diagonals are known.
Common Mistakes to Avoid
Calculating the perimeter of a rhombus can sometimes lead to errors. Here are some common mistakes and tips to avoid them:
-
Using Incorrect Side Length:
Ensure that all sides of the rhombus are equal. Double-check the side measurements before using the formula \( P = 4a \), where \( a \) is the side length.
-
Confusing Diagonals with Side Lengths:
The diagonals of a rhombus are not the same as its sides. When given the lengths of the diagonals, use the correct formula \( P = 2 \sqrt{p^2 + q^2} \), where \( p \) and \( q \) are the diagonals.
-
Incorrectly Applying the Pythagorean Theorem:
When using the diagonals to find the side length, ensure that you apply the Pythagorean theorem correctly. For example, if the diagonals are \( p \) and \( q \), then the side length \( a \) can be found using \( a = \sqrt{\left(\frac{p}{2}\right)^2 + \left(\frac{q}{2}\right)^2} \).
-
Ignoring Units:
Always ensure that all measurements are in the same unit. Convert them if necessary before performing any calculations.
-
Forgetting to Square the Diagonals:
When calculating the perimeter using diagonals, remember to square the lengths of the diagonals before summing them. The formula is \( P = 2 \sqrt{p^2 + q^2} \), not \( P = 2 \sqrt{p + q} \).
-
Calculation Errors:
Double-check your calculations, especially when dealing with square roots and multiplications. Small arithmetic errors can lead to incorrect results.
By being mindful of these common pitfalls, you can accurately calculate the perimeter of a rhombus.
Practical Applications of Rhombus Perimeter
The perimeter of a rhombus is an essential geometric concept with various practical applications in real-life scenarios. Understanding how to calculate and apply the perimeter can be beneficial in several fields and daily activities. Here are some notable applications:
- Architecture and Construction:
The perimeter of a rhombus is often used in architectural designs and construction projects. For instance, when designing buildings, parks, or plazas with rhombus-shaped elements, knowing the perimeter helps in calculating materials needed and ensuring precise construction.
- Interior Design:
In interior design, rhombus shapes are used for creating aesthetically pleasing patterns on floors, walls, and ceilings. The perimeter calculation aids in the planning and implementation of these designs, ensuring symmetry and balance.
- Landscaping:
Landscapers use rhombus shapes for creating unique garden layouts, pathways, and other outdoor features. Calculating the perimeter allows for accurate measurements and efficient use of space and resources.
- Crafts and Hobbies:
For crafting projects, such as quilting or creating decorative items, understanding the perimeter of a rhombus helps in cutting fabric or materials accurately. It ensures that pieces fit together perfectly, resulting in high-quality craftsmanship.
- Sports Fields:
In sports, especially baseball, the diamond-shaped infield is essentially a rhombus. Knowing the perimeter is crucial for designing the field to standard dimensions and maintaining it properly.
- Technology and Engineering:
In fields like engineering and robotics, rhombus shapes are sometimes used in the design of components and structures. Calculating the perimeter is necessary for the precise fabrication and assembly of these parts.
Overall, the practical applications of the perimeter of a rhombus are diverse and significant. From enhancing aesthetic appeal to ensuring structural integrity, understanding this concept is valuable across various disciplines.
Conclusion and Summary
In this article, we explored various aspects of the rhombus, focusing particularly on its perimeter. Understanding the perimeter of a rhombus is essential for solving geometric problems and has practical applications in fields such as architecture, engineering, and design.
We started with a definition of a rhombus, emphasizing its unique properties such as equal side lengths and bisecting diagonals. The fundamental formula for the perimeter of a rhombus was discussed, which is simply four times the length of one side:
Additionally, we examined alternative methods to determine the perimeter, such as using the lengths of the diagonals. Applying the Pythagorean Theorem to find the side length when the diagonals are known provided a deeper understanding of the relationships within a rhombus.
Key points to remember include:
- The perimeter formula: \( P = 4a \)
- Using the Pythagorean Theorem for calculating side length when diagonals are given.
- Avoiding common mistakes such as confusing the properties of rhombuses with those of other quadrilaterals.
The practical applications of calculating the perimeter of a rhombus demonstrate the importance of mastering these concepts. From creating efficient designs to solving real-world problems, the knowledge of geometric properties is invaluable.
By understanding these principles, you can confidently approach problems involving rhombuses, ensuring accurate and efficient solutions. This comprehensive overview of the perimeter of a rhombus should serve as a solid foundation for further study and application.
Hướng dẫn cách tính chu vi hình thoi một cách chi tiết và dễ hiểu. Video này phù hợp cho những ai đang tìm hiểu về công thức chu vi hình thoi.
Cách Tính Chu Vi Hình Thoi
READ MORE:
Hướng dẫn chi tiết về cách tính diện tích và chu vi của hình thoi để giúp bạn nắm vững kiến thức và áp dụng vào thực tế.
Cách tìm Diện Tích và Chu Vi của Hình Thoi