Topic perimeter of right triangle formula: Discover the simple steps to calculate the perimeter of a right triangle with our comprehensive guide. Learn how to use the perimeter formula effectively, understand the role of the Pythagorean theorem, and apply these methods to real-world problems. Mastering this fundamental geometry concept has never been easier!
Table of Content
- Perimeter of a Right Triangle
- Introduction to Right Triangles
- Understanding the Perimeter of a Right Triangle
- Basic Formula for Perimeter
- Steps to Calculate Perimeter
- Example Calculations
- Applications of Perimeter Formula
- Common Mistakes and How to Avoid Them
- Advanced Topics
- Practice Problems
- Conclusion
- YOUTUBE: Khám phá cách tính diện tích và chu vi của tam giác vuông với hướng dẫn dễ hiểu từ Thầy J. Hãy xem video này để nắm vững công thức và áp dụng vào bài tập của bạn.
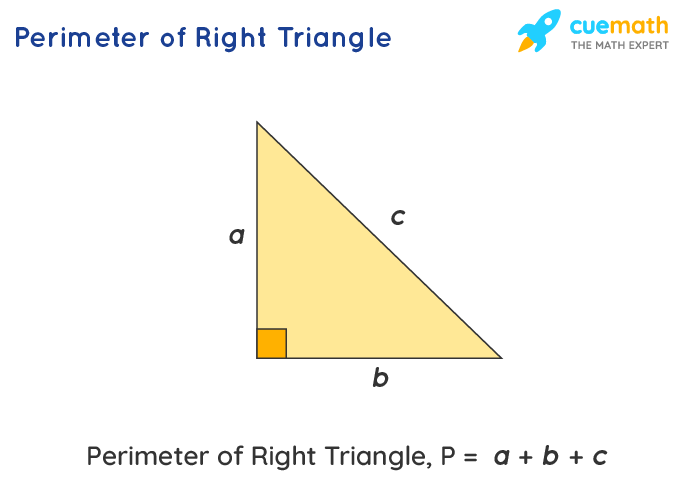
Perimeter of a Right Triangle
The perimeter of a right triangle can be calculated using the lengths of its three sides. A right triangle consists of two legs and one hypotenuse, where the hypotenuse is the side opposite the right angle and is the longest side of the triangle.
Formula
If the lengths of the two legs are a and b, and the hypotenuse is c, the perimeter P of the right triangle is given by:
\[ P = a + b + c \]
Using the Pythagorean Theorem
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. This can be written as:
\[ c = \sqrt{a^2 + b^2} \]
Substituting this into the perimeter formula, we get:
\[ P = a + b + \sqrt{a^2 + b^2} \]
Example Calculation
Consider a right triangle with legs of lengths 3 and 4 units.
- Calculate the length of the hypotenuse:
- Use the perimeter formula:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
\[ P = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of the triangle is 12 units.
Summary
To find the perimeter of a right triangle, add the lengths of the two legs and the hypotenuse. The hypotenuse can be found using the Pythagorean Theorem. The formula for the perimeter is:
\[ P = a + b + \sqrt{a^2 + b^2} \]
Understanding this formula allows for easy calculation of the perimeter of any right triangle when the lengths of the legs are known.

READ MORE:
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring exactly 90 degrees. This special property makes right triangles unique and allows for the use of specific mathematical formulas and theorems to solve for their properties.
Here are some key characteristics of right triangles:
- One Right Angle: A right triangle always includes one 90-degree angle.
- Hypotenuse: The side opposite the right angle is the hypotenuse, which is the longest side of the triangle.
- Legs: The two sides that form the right angle are called legs.
The fundamental properties of right triangles are essential for various calculations in geometry. Understanding these properties allows for the application of the Pythagorean theorem and other formulas to solve problems involving right triangles.
In a right triangle with legs a and b, and hypotenuse c, the Pythagorean theorem states:
\[ c^2 = a^2 + b^2 \]
Using this theorem, you can determine the length of any side if the lengths of the other two sides are known.
Right triangles are fundamental in trigonometry, allowing for the definition and use of trigonometric ratios such as sine, cosine, and tangent. These ratios relate the angles of a right triangle to the lengths of its sides:
- Sine: \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \)
- Cosine: \( \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- Tangent: \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)
These properties and formulas make right triangles a crucial element in geometry, trigonometry, and various real-world applications. Whether you're calculating distances, angles, or areas, the principles of right triangles provide a reliable foundation for solving these problems.
Understanding the Perimeter of a Right Triangle
The perimeter of a right triangle is the total distance around the triangle, which is the sum of the lengths of its three sides. To find the perimeter, you need to know the lengths of the two legs and the hypotenuse of the right triangle.
Given a right triangle with legs a and b, and hypotenuse c, the formula for the perimeter P is:
\[ P = a + b + c \]
To use this formula effectively, follow these steps:
- Identify the lengths of the two legs, a and b.
- Calculate the length of the hypotenuse c using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of the two legs and the hypotenuse to find the perimeter: \[ P = a + b + \sqrt{a^2 + b^2} \]
Here's an example to illustrate these steps:
- Suppose the lengths of the legs are a = 3 and b = 4.
- First, calculate the hypotenuse: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Then, find the perimeter: \[ P = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of the triangle is 12 units.
Understanding the perimeter formula is essential for solving various geometric problems and real-world applications where knowing the boundary length is necessary. This straightforward calculation provides a foundation for more complex geometrical concepts and applications.
Basic Formula for Perimeter
The perimeter of a right triangle is the sum of the lengths of its three sides. This includes the two legs that form the right angle and the hypotenuse, which is the side opposite the right angle. The basic formula for the perimeter P of a right triangle is:
\[ P = a + b + c \]
Where:
- a is the length of one leg
- b is the length of the other leg
- c is the length of the hypotenuse
To calculate the perimeter, follow these steps:
- Measure the lengths of the two legs, a and b.
- Calculate the length of the hypotenuse c using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of the two legs and the hypotenuse to find the perimeter: \[ P = a + b + \sqrt{a^2 + b^2} \]
Consider an example where the lengths of the legs are a = 6 and b = 8:
- First, calculate the hypotenuse: \[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
- Next, find the perimeter: \[ P = 6 + 8 + 10 = 24 \]
Therefore, the perimeter of the triangle is 24 units.
This basic formula for the perimeter of a right triangle is fundamental in geometry. It allows you to determine the total length around the triangle, which is useful in various practical and theoretical applications.
Steps to Calculate Perimeter
Calculating the perimeter of a right triangle involves determining the sum of the lengths of its three sides. Follow these detailed steps to find the perimeter:
- Identify the lengths of the two legs of the right triangle, labeled as a and b.
- Use the Pythagorean Theorem to calculate the length of the hypotenuse c:
\[
c = \sqrt{a^2 + b^2}
\]
This step involves squaring the lengths of both legs, adding the squares together, and then taking the square root of the sum to find the hypotenuse.
- Add the lengths of the two legs and the hypotenuse to find the perimeter P: \[ P = a + b + c \]
Here’s an example to illustrate these steps:
- Suppose the lengths of the legs are a = 7 and b = 24.
- First, calculate the hypotenuse: \[ c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \]
- Next, find the perimeter: \[ P = 7 + 24 + 25 = 56 \]
Therefore, the perimeter of the triangle is 56 units.
Following these steps ensures that you accurately calculate the perimeter of any right triangle. This method is fundamental in geometry and can be applied to various practical and theoretical problems.
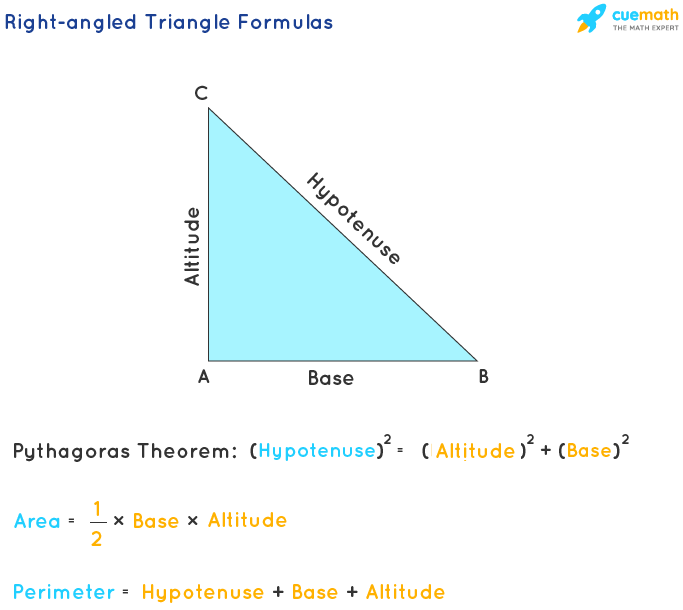
Example Calculations
Example calculations help illustrate the steps involved in determining the perimeter of a right triangle. Let's go through a couple of detailed examples:
Example 1
Consider a right triangle with legs a = 3 and b = 4.
- First, calculate the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Next, find the perimeter by adding the lengths of the legs and the hypotenuse: \[ P = a + b + c = 3 + 4 + 5 = 12 \]
Therefore, the perimeter of the triangle is 12 units.
Example 2
Consider a right triangle with legs a = 5 and b = 12.
- First, calculate the hypotenuse: \[ c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \]
- Next, find the perimeter: \[ P = a + b + c = 5 + 12 + 13 = 30 \]
Therefore, the perimeter of the triangle is 30 units.
Example 3
Consider a right triangle with legs a = 8 and b = 15.
- First, calculate the hypotenuse: \[ c = \sqrt{a^2 + b^2} = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17 \]
- Next, find the perimeter: \[ P = a + b + c = 8 + 15 + 17 = 40 \]
Therefore, the perimeter of the triangle is 40 units.
These example calculations demonstrate the step-by-step process of using the Pythagorean theorem to find the hypotenuse and then summing the sides to determine the perimeter of a right triangle. Practice these steps with different values to reinforce your understanding and proficiency in calculating the perimeter.
Applications of Perimeter Formula
The formula for the perimeter of a right triangle has numerous practical applications in various fields, including construction, navigation, design, and everyday problem-solving. Understanding how to apply this formula can help in a range of scenarios. Here are some detailed examples of its applications:
Construction and Architecture
In construction and architecture, accurate measurements are crucial for designing structures and ensuring they fit together properly. The perimeter formula is used to calculate the lengths of materials needed for framing, flooring, and other structural components.
- Framing: Determining the perimeter of triangular sections helps in estimating the amount of lumber or other materials required.
- Roofing: Calculating the perimeter of right triangular roof sections ensures proper fitting and material coverage.
Navigation and Surveying
In navigation and surveying, understanding distances and angles is essential. The perimeter formula helps in plotting courses and determining the lengths of boundary lines.
- Land Surveying: Surveyors use the perimeter formula to calculate property boundaries, ensuring accurate land measurements.
- Navigation: Mariners and pilots use geometric principles, including the perimeter formula, to chart courses and measure distances.
Design and Art
In design and art, geometric shapes are often used to create visually appealing compositions. Knowing the perimeter of right triangles helps in creating balanced and proportionate designs.
- Graphic Design: Designers use geometric calculations to create logos, layouts, and other visual elements with precise dimensions.
- Architecture: Architects incorporate right triangles in their designs, using the perimeter formula to ensure structural integrity and aesthetic appeal.
Everyday Problem-Solving
In everyday life, understanding the perimeter of right triangles can assist in a variety of tasks, from home improvement projects to recreational activities.
- DIY Projects: Calculating the perimeter of triangular garden beds, decks, or other home improvements ensures proper material usage and fit.
- Sports and Recreation: In activities such as hiking or orienteering, knowing the perimeter helps in planning routes and estimating travel distances.
By mastering the perimeter formula for right triangles, you can apply this knowledge to solve real-world problems efficiently and accurately. This fundamental geometric concept is not only essential for academic purposes but also invaluable in practical, everyday situations.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a right triangle involves some common pitfalls that can lead to incorrect results. Understanding these mistakes and learning how to avoid them will help ensure accurate calculations.
- Incorrect Identification of the Hypotenuse:
The hypotenuse is the longest side of a right triangle, opposite the right angle. A common mistake is to misidentify one of the legs as the hypotenuse. Ensure you correctly identify the hypotenuse, which can be verified by checking if it is the side opposite the right angle.
- Misapplication of the Pythagorean Theorem:
The Pythagorean Theorem states that \(a^2 + b^2 = c^2\), where \(c\) is the hypotenuse. Sometimes, the formula is incorrectly applied as \(a^2 + c^2 = b^2\) or \(b^2 + c^2 = a^2\). Always remember that \(c\) should be the hypotenuse.
- Forgetting to Include All Three Sides in the Perimeter Calculation:
After calculating the hypotenuse using the Pythagorean Theorem, a common mistake is to forget to add all three sides to find the perimeter. The correct formula is:
\[ \text{Perimeter} = a + b + c \]
- Using Incorrect Units:
Ensure that all measurements are in the same units before performing calculations. Mixing different units can lead to incorrect results. Convert all measurements to the same unit if necessary.
- Rounding Errors:
When using a calculator, rounding intermediate values can lead to errors in the final perimeter calculation. It’s best to use the full precision of your calculator until the final result, and then round as needed.
- Neglecting Decimal Precision:
For precise calculations, especially in fields such as engineering or architecture, it is important to maintain adequate decimal precision. Avoid truncating decimal places prematurely.
By being aware of these common mistakes and following the correct procedures, you can accurately calculate the perimeter of a right triangle and avoid errors that could compromise your results.
Advanced Topics
In this section, we delve deeper into the advanced aspects of calculating the perimeter of a right triangle and related geometric concepts.
1. Using the Distance Formula
When the coordinates of the vertices of a right triangle are given, the distance formula can be used to find the length of each side. The formula is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This formula helps in calculating the length of the sides when the vertices are known, which can then be used to find the perimeter.
2. Perimeter in Different Coordinate Systems
Understanding how to calculate the perimeter of a right triangle in different coordinate systems, such as polar coordinates, can be useful in advanced applications. For example, converting from polar to Cartesian coordinates before applying the distance formula:
\[
x = r \cos \theta
\]
\[
y = r \sin \theta
\]
3. Trigonometric Relationships
Trigonometry provides powerful tools to solve for unknown sides and angles in right triangles, which can then be used to determine the perimeter. Key trigonometric identities and relationships include:
- Sine: \(\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}\)
- Cosine: \(\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}\)
- Tangent: \(\tan \theta = \frac{\text{opposite}}{\text{adjacent}}\)
4. Complex Plane Analysis
Analyzing right triangles in the complex plane can be another advanced topic. When vertices are represented as complex numbers, distances can be computed using the modulus function:
\[
|z| = \sqrt{a^2 + b^2}
\]
Where \( z = a + bi \) is a complex number. This can then be applied to find the perimeter.
5. Perimeter of a Right Triangle with Incircle
The incircle of a right triangle touches all three sides. The radius \( r \) of the incircle can be used to express the perimeter \( P \) in terms of the triangle's sides \( a \), \( b \), and \( c \):
\[
r = \frac{a + b - c}{2}
\]
\p>
And hence the perimeter can be refined using this property.
6. Calculating Perimeter in Non-Euclidean Geometry
Exploring the properties of right triangles in non-Euclidean geometries, such as hyperbolic or spherical geometry, can offer insights into different perimeter calculations. For example, the sides of a hyperbolic triangle can be calculated using hyperbolic functions.
These advanced topics provide a comprehensive understanding of the various ways to approach the perimeter of right triangles, enhancing problem-solving skills in diverse mathematical contexts.
Practice Problems
Here are some practice problems to help you understand how to calculate the perimeter of a right triangle. Use the given information to find the perimeter for each problem. Remember to use the Pythagorean theorem if needed to find the missing side.
-
Given a right triangle with legs \(a = 3\) and \(b = 4\), calculate the perimeter.
- Step 1: Find the hypotenuse using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\)
- Step 2: Calculate \(c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
- Step 3: Calculate the perimeter: \(P = a + b + c = 3 + 4 + 5 = 12\)
-
Given a right triangle with legs \(a = 5\) and \(b = 12\), calculate the perimeter.
- Step 1: Find the hypotenuse using the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\)
- Step 2: Calculate \(c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13\)
- Step 3: Calculate the perimeter: \(P = a + b + c = 5 + 12 + 13 = 30\)
-
Given a right triangle with hypotenuse \(c = 10\) and one leg \(a = 6\), calculate the perimeter.
- Step 1: Find the other leg using the Pythagorean theorem: \(b = \sqrt{c^2 - a^2}\)
- Step 2: Calculate \(b = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8\)
- Step 3: Calculate the perimeter: \(P = a + b + c = 6 + 8 + 10 = 24\)
-
Given a right triangle with hypotenuse \(c = 17\) and one leg \(b = 15\), calculate the perimeter.
- Step 1: Find the other leg using the Pythagorean theorem: \(a = \sqrt{c^2 - b^2}\)
- Step 2: Calculate \(a = \sqrt{17^2 - 15^2} = \sqrt{289 - 225} = \sqrt{64} = 8\)
- Step 3: Calculate the perimeter: \(P = a + b + c = 8 + 15 + 17 = 40\)
These problems will help reinforce your understanding of how to calculate the perimeter of a right triangle. Practice solving these problems step-by-step, and use the Pythagorean theorem when necessary.
Conclusion
In conclusion, understanding the perimeter of a right triangle is fundamental in various mathematical and practical applications. The perimeter is simply the sum of all three sides of the triangle, which can be expressed as:
\[
\text{Perimeter} = a + b + c
\]
where \(a\) and \(b\) are the legs of the triangle and \(c\) is the hypotenuse. The Pythagorean Theorem plays a crucial role in calculating the hypotenuse when the lengths of the legs are known:
\[
c = \sqrt{a^2 + b^2}
\]
Thus, the perimeter formula can also be written as:
\[
\text{Perimeter} = a + b + \sqrt{a^2 + b^2}
\]
By mastering these formulas, one can efficiently solve problems involving the perimeter of right triangles. Whether for academic purposes, real-world construction, or design, this knowledge is highly valuable.
Moreover, recognizing common mistakes, such as incorrectly identifying the legs and the hypotenuse, ensures accuracy in calculations. Practicing with various examples and applying these concepts to different scenarios will further solidify your understanding and proficiency.
Ultimately, the ability to calculate the perimeter of right triangles not only enhances your mathematical skills but also prepares you for more advanced geometric and trigonometric studies.
Khám phá cách tính diện tích và chu vi của tam giác vuông với hướng dẫn dễ hiểu từ Thầy J. Hãy xem video này để nắm vững công thức và áp dụng vào bài tập của bạn.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán Học với Thầy J
READ MORE:
Hướng dẫn chi tiết cách tính diện tích và chu vi của tam giác vuông. Xem video để hiểu rõ công thức và cách áp dụng vào bài tập của bạn.
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông