Topic perimeter of a right triangle formula: Understanding the perimeter of a right triangle is crucial for students and professionals alike. This guide will provide a clear and concise formula for calculating the perimeter, along with examples and practical applications. Whether you're solving math problems or applying geometry in real life, this article will make the concept easy to grasp.
Table of Content
- Perimeter of a Right Triangle Formula
- Introduction to Right Triangles
- Understanding the Components of a Right Triangle
- Definition of Perimeter
- Formula for Perimeter of a Right Triangle
- Deriving the Perimeter Formula Using the Pythagorean Theorem
- Step-by-Step Calculation of the Perimeter
- Examples and Practice Problems
- Applications of Right Triangle Perimeter in Real Life
- Common Mistakes and How to Avoid Them
- Advanced Topics Related to Right Triangles
- Conclusion
- YOUTUBE:
Perimeter of a Right Triangle Formula
The perimeter of a right triangle can be calculated by summing the lengths of all three sides. A right triangle has one right angle (90 degrees) and two other angles. The sides of a right triangle are typically referred to as:
- a - One of the legs of the triangle
- b - The other leg of the triangle
- c - The hypotenuse, which is the longest side opposite the right angle
The formula to find the perimeter (P) of a right triangle is given by:
\[
P = a + b + c
\]
Calculating the Hypotenuse
In a right triangle, the hypotenuse can be found using the Pythagorean theorem, which states:
\[
c = \sqrt{a^2 + b^2}
\]
Thus, the perimeter formula can also be expressed in terms of the legs a and b as:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Example Calculation
Consider a right triangle with legs a = 3 units and b = 4 units. To find the perimeter:
- Calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Sum the sides to find the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Thus, the perimeter of the right triangle is 12 units.

Introduction to Right Triangles
A right triangle is a type of triangle that has one angle exactly equal to 90 degrees. This unique property makes right triangles fundamental in geometry and trigonometry. Understanding the properties and components of right triangles is essential for solving various mathematical problems.
Right triangles have three sides:
- Legs: The two sides that form the right angle. These are often labeled as a and b.
- Hypotenuse: The side opposite the right angle, labeled as c. It is the longest side of the right triangle.
The Pythagorean theorem is a fundamental principle that relates the lengths of the sides of a right triangle:
\[
a^2 + b^2 = c^2
\]
This theorem allows us to calculate the length of any side if the lengths of the other two sides are known. For example, if the lengths of the legs a and b are known, the length of the hypotenuse c can be calculated as follows:
\[
c = \sqrt{a^2 + b^2}
\]
Right triangles are widely used in various fields such as architecture, engineering, and physics due to their simplicity and the ease of applying the Pythagorean theorem. Understanding the basics of right triangles provides a foundation for exploring more complex geometric concepts.
Understanding the Components of a Right Triangle
To fully grasp the concept of a right triangle, it's important to understand its components and their relationships. A right triangle consists of three sides and three angles, with the key feature being one angle that measures 90 degrees. Here are the main components:
- Legs (a and b): These are the two sides that form the right angle. They are perpendicular to each other and are often referred to as the base and height of the triangle.
- Hypotenuse (c): This is the side opposite the right angle and is the longest side of the right triangle. The hypotenuse is always longer than either of the legs.
- Right Angle: This is the 90-degree angle formed by the two legs. It is the defining characteristic of a right triangle.
- Other Angles: The other two angles in a right triangle are acute angles, each measuring less than 90 degrees. These angles add up to 90 degrees since the total sum of angles in any triangle is 180 degrees.
The relationship between these components is governed by the Pythagorean theorem, which states:
\[
a^2 + b^2 = c^2
\]
This theorem is crucial for calculating the length of any side if the lengths of the other two sides are known. Let's break down each component in detail:
- Calculating the Hypotenuse:
Given the lengths of the legs a and b, the hypotenuse c can be found using the formula:
\[
c = \sqrt{a^2 + b^2}
\] - Finding a Leg:
If the hypotenuse c and one leg a are known, the other leg b can be calculated as:
\[
b = \sqrt{c^2 - a^2}
\] - Angle Calculation:
The acute angles can be calculated using trigonometric ratios. For example, if a is the adjacent leg and b is the opposite leg:
\[
\tan(\theta) = \frac{b}{a}
\]
\[
\theta = \arctan\left(\frac{b}{a}\right)
\]
Understanding these components and their relationships helps in solving various geometric problems and applying these principles in real-world scenarios, such as in construction and design.
Definition of Perimeter
The perimeter of a geometric shape is defined as the total distance around the outside of the shape. For polygons, it is the sum of the lengths of all the sides. In the case of a right triangle, the perimeter is the sum of the lengths of its three sides: the two legs and the hypotenuse.
Mathematically, the perimeter (P) of a right triangle with legs a and b, and hypotenuse c is given by the formula:
\[
P = a + b + c
\]
To find the perimeter step by step, follow these instructions:
- Identify the lengths of the legs:
- Let a be the length of one leg.
- Let b be the length of the other leg.
- Calculate the hypotenuse:
Use the Pythagorean theorem to find the length of the hypotenuse c:
\[
c = \sqrt{a^2 + b^2}
\] - Add the lengths of all sides:
Sum the lengths of the legs and the hypotenuse to get the perimeter:
\[
P = a + b + c
\]
For example, if a right triangle has legs of lengths 3 units and 4 units, the hypotenuse can be calculated as follows:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Thus, the perimeter is:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Understanding the concept of perimeter is crucial in various applications such as construction, land surveying, and any field that involves measuring and outlining shapes.
Formula for Perimeter of a Right Triangle
The perimeter of a right triangle is the total length around the triangle. It is calculated by adding together the lengths of the triangle's three sides: the two legs and the hypotenuse. Here's a detailed look at the formula and how to apply it.
The general formula for the perimeter (P) of a right triangle with legs a and b, and hypotenuse c is:
\[
P = a + b + c
\]
To apply this formula, follow these steps:
- Determine the lengths of the legs:
- Identify the lengths of the legs, a and b, of the right triangle.
- Calculate the hypotenuse:
Use the Pythagorean theorem to find the length of the hypotenuse c:
\[
c = \sqrt{a^2 + b^2}
\] - Add the lengths of the sides:
Sum the lengths of the two legs and the hypotenuse to find the perimeter:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Let's go through an example for clarity. Suppose we have a right triangle with legs of lengths 5 units and 12 units.
- First, identify the lengths of the legs: a = 5 units and b = 12 units.
- Next, calculate the hypotenuse:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
\] - Finally, sum the lengths of all three sides to find the perimeter:
\[
P = 5 + 12 + 13 = 30 \text{ units}
\]
Thus, the perimeter of the right triangle with legs 5 units and 12 units is 30 units.
Using this step-by-step method ensures that you can accurately calculate the perimeter of any right triangle, which is a fundamental skill in geometry and practical applications such as construction and design.
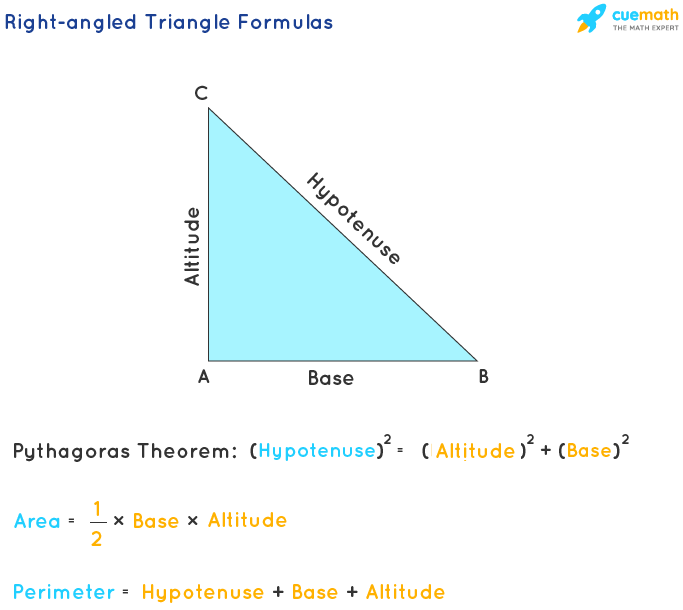
Deriving the Perimeter Formula Using the Pythagorean Theorem
The perimeter of a right triangle is the total length around the triangle. To derive the formula for the perimeter using the Pythagorean theorem, we need to understand the relationship between the sides of a right triangle. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b):
\[
a^2 + b^2 = c^2
\]
Given this relationship, we can follow these steps to derive the perimeter formula:
- Identify the lengths of the legs:
- Let a and b be the lengths of the legs of the right triangle.
- Calculate the hypotenuse:
Using the Pythagorean theorem, the length of the hypotenuse c is:
\[
c = \sqrt{a^2 + b^2}
\] - Derive the perimeter formula:
The perimeter (P) is the sum of the lengths of all three sides:
\[
P = a + b + c
\]
Substituting the expression for c from the Pythagorean theorem, we get:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Let's go through an example to illustrate the derivation. Suppose we have a right triangle with legs a = 6 units and b = 8 units.
- First, identify the lengths of the legs: a = 6 units and b = 8 units.
- Next, calculate the hypotenuse:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
\] - Finally, sum the lengths of all three sides to find the perimeter:
\[
P = 6 + 8 + 10 = 24 \text{ units}
\]
Thus, the perimeter of the right triangle with legs 6 units and 8 units is 24 units. By following these steps, we can derive and apply the perimeter formula using the Pythagorean theorem for any right triangle.
Step-by-Step Calculation of the Perimeter
Calculating the perimeter of a right triangle involves finding the sum of its three sides: the two legs and the hypotenuse. Follow these steps to perform the calculation:
- Identify the lengths of the legs:
- Let a be the length of one leg.
- Let b be the length of the other leg.
- Calculate the hypotenuse:
Use the Pythagorean theorem to find the length of the hypotenuse c:
\[
c = \sqrt{a^2 + b^2}
\] - Sum the lengths of the sides:
Add the lengths of the two legs and the hypotenuse to get the perimeter:
\[
P = a + b + c
\]
Substituting the value of c from the Pythagorean theorem, the formula becomes:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Let's go through a detailed example to illustrate the process:
Suppose we have a right triangle with legs of lengths 7 units and 24 units.
- First, identify the lengths of the legs: a = 7 units and b = 24 units.
- Next, calculate the hypotenuse:
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25
\] - Finally, sum the lengths of all three sides to find the perimeter:
\[
P = 7 + 24 + 25 = 56 \text{ units}
\]
Thus, the perimeter of the right triangle with legs 7 units and 24 units is 56 units.
By following these steps, you can accurately calculate the perimeter of any right triangle, ensuring a clear understanding of the relationship between its sides and the application of the Pythagorean theorem.
Examples and Practice Problems
Understanding how to calculate the perimeter of a right triangle can be reinforced through examples and practice problems. Below are several examples that demonstrate the step-by-step process, followed by practice problems for you to solve.
Example 1
- Identify the lengths of the legs:
Let a = 3 units and b = 4 units.
- Calculate the hypotenuse:
Using the Pythagorean theorem:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Find the perimeter:
Sum the lengths of all sides:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Example 2
- Identify the lengths of the legs:
Let a = 6 units and b = 8 units.
- Calculate the hypotenuse:
Using the Pythagorean theorem:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
\] - Find the perimeter:
Sum the lengths of all sides:
\[
P = 6 + 8 + 10 = 24 \text{ units}
\]
Practice Problems
- Problem 1:
Find the perimeter of a right triangle with legs of lengths 5 units and 12 units.
Solution:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
\]
\[
P = 5 + 12 + 13 = 30 \text{ units}
\] - Problem 2:
Find the perimeter of a right triangle with legs of lengths 9 units and 12 units.
Solution:
\[
c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15
\]
\[
P = 9 + 12 + 15 = 36 \text{ units}
\] - Problem 3:
Find the perimeter of a right triangle with legs of lengths 8 units and 15 units.
Solution:
\[
c = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17
\]
\[
P = 8 + 15 + 17 = 40 \text{ units}
\]
By practicing these problems, you can become more comfortable with calculating the perimeter of right triangles and applying the Pythagorean theorem.
Applications of Right Triangle Perimeter in Real Life
The perimeter of a right triangle is a useful measurement in various real-life scenarios, helping solve practical problems in different fields. Here are some notable applications:
-
Construction and Carpentry:
In construction, knowing the perimeter of right triangles helps in framing structures, designing roof trusses, and ensuring walls and corners are correctly aligned. Carpenters often use right triangles to create precise angles and fit elements together accurately.
-
Architecture:
Architects use the perimeter of right triangles to calculate the lengths of walls and supports, ensuring buildings are stable and properly designed. This measurement aids in the accurate estimation of materials needed for construction projects.
-
Navigation:
Right triangles are essential in navigation for determining distances. By calculating the perimeter, navigators can find the distance between points, which is crucial for plotting courses and ensuring safe travel, particularly at sea.
-
Surveying:
Surveyors use right triangle calculations to measure land, determine property boundaries, and create maps. The perimeter helps in estimating distances and areas, providing accurate data for land development and construction planning.
-
Astronomy:
In astronomy, right triangles assist in calculating the distance between celestial bodies. The perimeter measurement helps astronomers understand spatial relationships and movements of planets, stars, and other astronomical objects.
-
Sports:
In sports, the perimeter of right triangles is used to design and mark fields, courts, and tracks. Accurate measurements ensure that the dimensions comply with regulations and provide fair conditions for all participants.
-
Home Improvement:
Homeowners often use right triangle measurements for various improvement projects. Whether installing new flooring, tiling, or building custom furniture, understanding the perimeter ensures precise cuts and proper material estimation.
Overall, the perimeter of a right triangle is a fundamental concept that finds practical applications in numerous fields, enhancing accuracy and efficiency in various tasks.

Common Mistakes and How to Avoid Them
Understanding and avoiding common mistakes in calculating the perimeter of a right triangle is crucial for accurate results. Here are some frequent errors and tips to prevent them:
- Incorrect Use of the Pythagorean Theorem:
One common mistake is misapplying the Pythagorean theorem. Remember, the theorem is only valid for right triangles, and it states that \(c^2 = a^2 + b^2\), where \(c\) is the hypotenuse. Ensure you're using it correctly by identifying the sides properly.
- Tip: Always double-check which side is the hypotenuse (the longest side opposite the right angle).
- Forgetting to Include All Three Sides:
Sometimes, students forget to add all three sides when calculating the perimeter. The perimeter formula is \(P = a + b + c\), where \(a\) and \(b\) are the legs, and \(c\) is the hypotenuse.
- Tip: Write down the formula and ensure each side length is accounted for in your calculation.
- Incorrect Measurements:
Using incorrect or inconsistent units can lead to errors. Ensure all measurements are in the same unit before calculating the perimeter.
- Tip: Standardize the units of measurement (e.g., convert all lengths to meters) before performing calculations.
- Arithmetic Errors:
Simple addition mistakes can occur when summing the side lengths. These errors are easily overlooked but can significantly affect the result.
- Tip: Double-check your arithmetic, and use a calculator for accuracy.
- Misidentifying Triangle Types:
Applying the right triangle formulas to non-right triangles is a common error. Ensure the triangle in question has a right angle before using the specific perimeter formula for right triangles.
- Tip: Verify the presence of a right angle by checking that one angle measures \(90^\circ\).
By being aware of these common mistakes and following these tips, you can improve your accuracy in calculating the perimeter of right triangles.
Advanced Topics Related to Right Triangles
Exploring right triangles leads to numerous advanced mathematical concepts and applications. Below are some of the key advanced topics related to right triangles:
-
Pythagorean Triples
Pythagorean triples are sets of three positive integers \( (a, b, c) \) that satisfy the equation \( a^2 + b^2 = c^2 \). These sets represent the side lengths of right triangles where all sides are whole numbers. Common examples include (3, 4, 5) and (5, 12, 13). Understanding and generating Pythagorean triples is essential in number theory and various applications in cryptography and computer science.
-
Trigonometric Functions
Right triangles are fundamental in trigonometry. The primary trigonometric functions—sine, cosine, and tangent—are defined based on the ratios of the sides of a right triangle. These functions are crucial in fields such as engineering, physics, and computer graphics.
-
Special Right Triangles
Special right triangles, such as the 45°-45°-90° and 30°-60°-90° triangles, have side length ratios that are consistent and can simplify complex geometric and trigonometric problems. For example, in a 45°-45°-90° triangle, the sides are in the ratio 1:1:√2.
-
Applications in Coordinate Geometry
Right triangles are used in coordinate geometry to calculate distances between points, slopes of lines, and to define geometric transformations such as rotations and reflections. The distance formula and the midpoint formula are directly derived from the Pythagorean theorem.
-
Heron's Formula
Heron's formula allows the calculation of the area of any triangle when the lengths of all three sides are known. For a right triangle, this can be particularly useful in verifying the area derived from the standard area formula \( \frac{1}{2} \times \text{base} \times \text{height} \).
-
Circumcircle and Incircle
The circumcircle of a right triangle has a radius equal to half the length of the hypotenuse. The incircle is the largest circle that fits inside the triangle and touches all three sides. These concepts are significant in geometry and help solve complex problems involving circles and triangles.
-
Advanced Geometric Constructions
Using right triangles, one can perform various geometric constructions such as constructing perpendicular bisectors, angle bisectors, and other essential elements in advanced geometric proofs and designs.
-
Applications in Real Life
Right triangles are extensively used in real life, especially in architecture, engineering, and construction. For instance, they help in creating structures with precise right angles and determining the heights of tall objects using indirect measurement techniques like trigonometry.
Conclusion
The perimeter of a right triangle is a fundamental concept in geometry that has numerous applications in both academic and practical fields. Understanding how to calculate the perimeter involves knowing the lengths of all three sides of the triangle, which can be achieved using the Pythagorean theorem for cases where the hypotenuse is unknown.
To summarize, the perimeter \( P \) of a right triangle with sides \( a \), \( b \), and hypotenuse \( c \) is given by:
\[ P = a + b + c \]
Here are the key points to remember:
- The perimeter is the total length around the triangle.
- If any two sides are known, the third can be calculated using the Pythagorean theorem \( c^2 = a^2 + b^2 \).
- The concept of perimeter is useful in real-life applications such as construction, navigation, and design.
By mastering this concept, one can solve various geometric problems and apply these solutions to real-world scenarios. The understanding and application of the perimeter of a right triangle illustrate the importance of basic geometric principles in everyday life and advanced fields alike.
Whether for academic purposes or practical applications, knowing how to calculate and use the perimeter of a right triangle is an essential skill that enhances both mathematical understanding and problem-solving abilities.
Continue practicing with different sets of problems to reinforce this knowledge, and explore advanced topics related to right triangles to deepen your comprehension and proficiency in geometry.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán với Thầy J
Cách tìm Diện Tích và Chu Vi của Tam Giác Vuông
