Topic how do you find perimeter of a hexagon: Discover the methods to find the perimeter of a hexagon, whether regular or irregular. This article explores formulas, step-by-step calculations, and practical examples to help you understand and apply the concepts. Enhance your math skills and easily determine the perimeter of any hexagon with our detailed guide.
Table of Content
- Perimeter of a Hexagon
- Introduction to Hexagons
- Definition and Basic Properties
- Types of Hexagons
- Formula for Perimeter of a Regular Hexagon
- Formula for Perimeter of an Irregular Hexagon
- Calculating the Perimeter with Given Side Length
- Calculating the Perimeter with Given Area
- Calculating the Perimeter with Coordinates of Vertices
- Hexagons Inscribed in Circles
- Real-life Applications
- Solved Examples
- Practice Problems
- Common Mistakes and Tips
- Conclusion
- YOUTUBE:
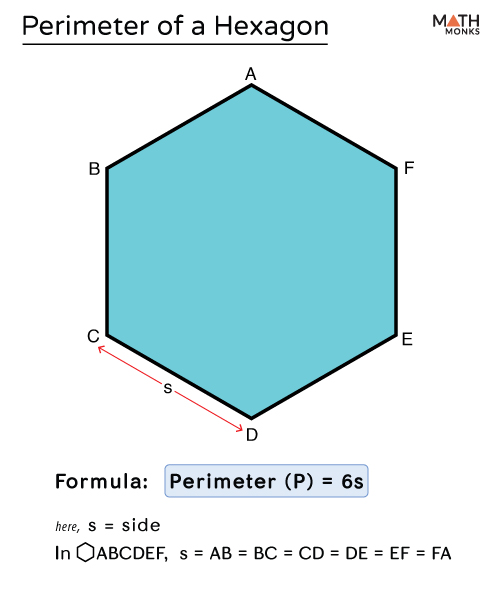
Perimeter of a Hexagon
The perimeter of a hexagon is the total distance covered around its edge. A hexagon is a polygon with six sides and six angles. There are different methods to calculate the perimeter depending on whether the hexagon is regular or irregular.
Formula for Regular Hexagon
For a regular hexagon, where all six sides are equal, the formula to calculate the perimeter is straightforward:
\[
P = 6s
\]
Where \( P \) is the perimeter and \( s \) is the length of one side.
Examples
- If a hexagon has a side length of 7.3 cm, the perimeter \( P \) is: \[ P = 6 \times 7.3 = 43.8 \text{ cm} \]
- If the area of a regular hexagon is known, for instance, 54\(\sqrt{3}\) square meters, the side length \( s \) can be found using the formula for the area of a hexagon: \[ A = \frac{3\sqrt{3}}{2} s^2 \] Solving for \( s \): \[ s^2 = \frac{2 \times 54\sqrt{3}}{3\sqrt{3}} = 36 \quad \Rightarrow \quad s = 6 \text{ meters} \] Thus, the perimeter \( P \) is: \[ P = 6 \times 6 = 36 \text{ meters} \]
Formula for Irregular Hexagon
For an irregular hexagon, where the sides are not all equal, the perimeter is calculated by summing the lengths of all six sides:
\[
P = s_1 + s_2 + s_3 + s_4 + s_5 + s_6
\]
Example
Given an irregular hexagon with sides of lengths 4.2, 4.3, 1.52, 5.4, 9.2, and 3.1 mm, the perimeter \( P \) is:
\[
P = 4.2 + 4.3 + 1.52 + 5.4 + 9.2 + 3.1 = 27.72 \text{ mm}
\]
Hexagon Properties
- A hexagon has six sides, six angles, and six vertices.
- The sum of the interior angles of a hexagon is 720 degrees.
- A regular hexagon can be divided into six equilateral triangles.
- There are different types of hexagons: regular, irregular, concave, and convex.

READ MORE:
Introduction to Hexagons
A hexagon is a polygon with six sides, six vertices, and six angles. The term "hexagon" is derived from the Greek words "hexa," meaning six, and "gonia," meaning angle. Hexagons can be found in various forms in nature and everyday objects, such as honeycombs, floor tiles, and the shape of a pencil's cross-section.
Hexagons are classified into regular and irregular hexagons. A regular hexagon has all sides and interior angles equal, with each interior angle measuring 120 degrees. Regular hexagons have symmetrical properties and can be divided into six equilateral triangles. Irregular hexagons have sides and angles of different lengths and measures.
Hexagons also exhibit interesting properties regarding their angles and diagonals. The sum of the interior angles of any hexagon is 720 degrees. Hexagons have nine diagonals, which can be categorized into short and long diagonals in the case of regular hexagons. The six short diagonals do not pass through the center, while the three long diagonals do.
Hexagons can be convex or concave. A convex hexagon has all interior angles less than 180 degrees, and all vertices point outward. In contrast, a concave hexagon has at least one interior angle greater than 180 degrees, and at least one vertex points inward.
Understanding hexagons is crucial in various fields, including geometry, architecture, and engineering, due to their unique properties and prevalence in natural and man-made structures.
Definition and Basic Properties
A hexagon is a six-sided polygon, which means it has six edges and six vertices. The term "hexagon" is derived from the Greek words "hex," meaning six, and "gonia," meaning angles. In a regular hexagon, all sides and angles are equal, making it a highly symmetrical shape.
- A regular hexagon has six equal sides and six equal interior angles of 120 degrees each.
- The sum of all interior angles in any hexagon is 720 degrees.
- Hexagons can be classified into different types: regular, irregular, convex, and concave.
Regular Hexagon
In a regular hexagon, all sides are of equal length, and all internal angles are 120 degrees. This type of hexagon is often seen in tiling patterns and natural formations like honeycombs.
Irregular Hexagon
An irregular hexagon has sides and angles of different lengths and measures. It does not have the same symmetry as a regular hexagon.
Convex Hexagon
A convex hexagon has all interior angles less than 180 degrees, and none of its vertices point inward.
Concave Hexagon
A concave hexagon has at least one interior angle greater than 180 degrees, causing at least one vertex to point inward.
Properties of a Regular Hexagon
- All sides are of equal length.
- All interior angles measure 120 degrees each.
- The sum of the interior angles is 720 degrees.
- It has six lines of symmetry.
- A regular hexagon can be divided into six equilateral triangles.
Types of Hexagons
A hexagon is a six-sided polygon with six angles. Depending on the lengths of its sides and the measures of its angles, hexagons can be classified into several types. Here are the main types of hexagons:
- Regular Hexagon
A regular hexagon has all six sides of equal length and all six interior angles of equal measure (120 degrees each). It exhibits symmetry, with six lines of symmetry and rotational symmetry of order 6.
- All sides are equal in length.
- All interior angles measure 120 degrees.
- It can be divided into six equilateral triangles.
- Opposite sides are parallel.
- It is also a convex hexagon.
- Irregular Hexagon
An irregular hexagon has sides and angles that are not all equal. The lengths of the sides and the measures of the angles can vary.
- Concave Hexagon
A concave hexagon has at least one interior angle greater than 180 degrees. If the vertices point inward, it forms a concave shape.
- Convex Hexagon
A convex hexagon has all interior angles less than 180 degrees. The vertices of a convex hexagon point outward, and it can be either regular or irregular.
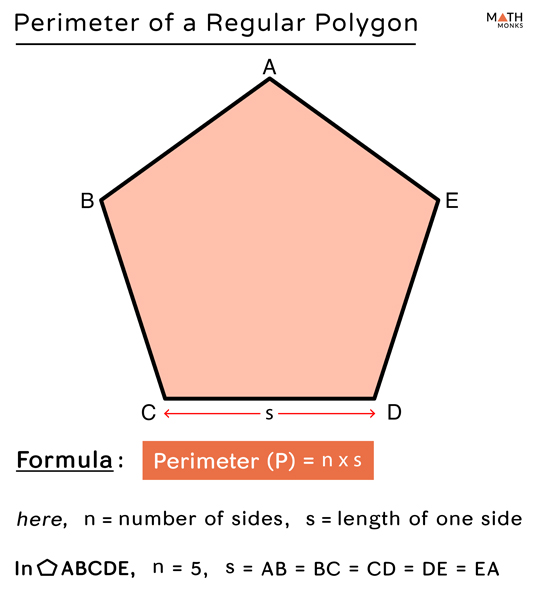
Formula for Perimeter of a Regular Hexagon
A regular hexagon is a six-sided polygon with all sides and internal angles equal. The formula to find the perimeter of a regular hexagon is straightforward and involves simply multiplying the length of one side by six.
The perimeter \(P\) of a regular hexagon with side length \(a\) is given by:
\[ P = 6 \times a \]
Where:
- \(a\) is the length of one side of the hexagon.
Here are the steps to calculate the perimeter:
- Measure the length of one side of the hexagon.
- Multiply the length by six.
- The result is the perimeter of the hexagon.
For example, if each side of the hexagon is 5 cm, the perimeter \(P\) is calculated as follows:
\[ P = 6 \times 5 = 30 \text{ cm} \]
This method applies only to regular hexagons, where all sides are equal. For irregular hexagons, the perimeter would be the sum of the lengths of all six sides.
| Side Length (a) | Perimeter (P) |
| 1 cm | 6 cm |
| 2 cm | 12 cm |
| 3 cm | 18 cm |
| 4 cm | 24 cm |
Understanding the formula for the perimeter of a regular hexagon helps in various practical applications, from geometry problems to real-world uses in design and construction.

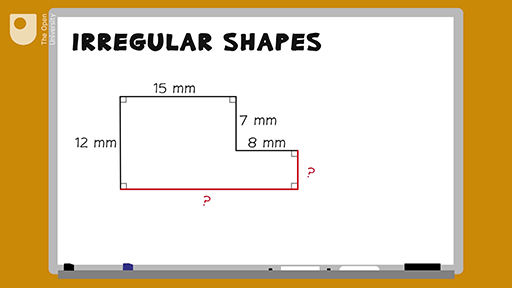
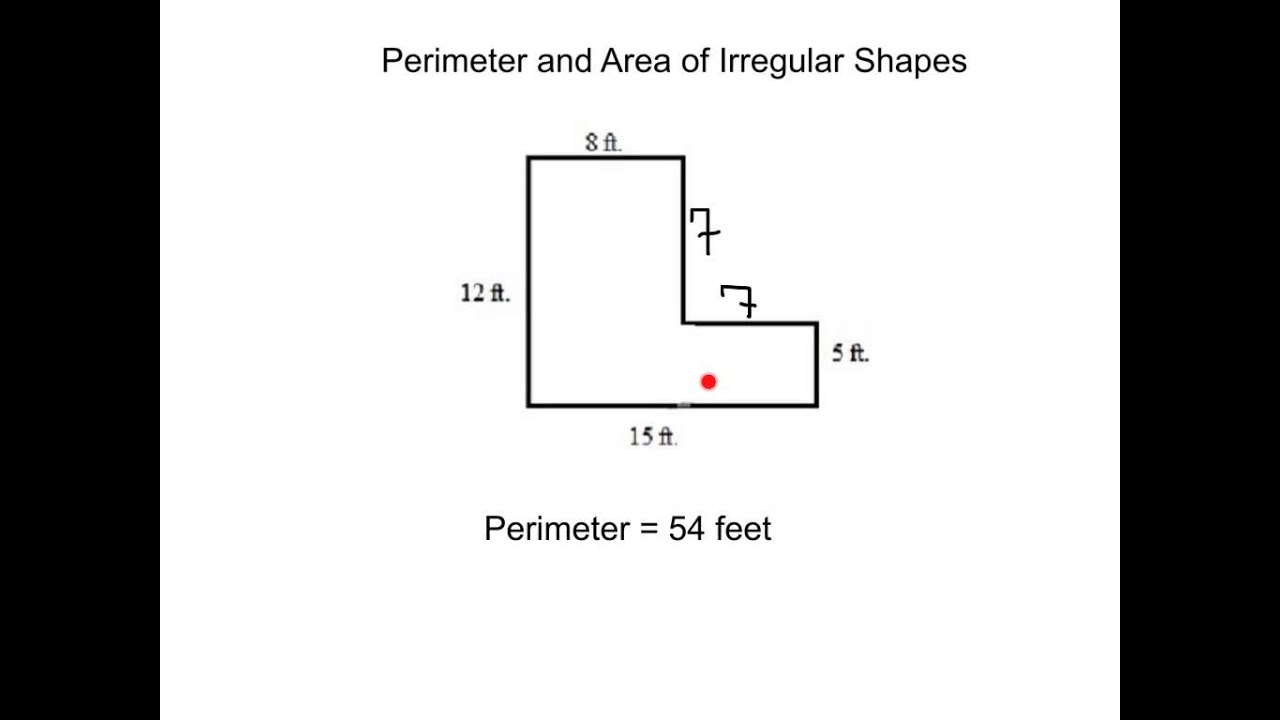
Formula for Perimeter of an Irregular Hexagon
The perimeter of an irregular hexagon is the total distance around the six-sided figure, where the sides can be of different lengths. To find the perimeter, simply add up the lengths of all six sides.
- Step 1: Measure the length of each side of the hexagon.
- Step 2: Add the lengths of all six sides together.
For example, if the sides of an irregular hexagon are 9 cm, 10 cm, 14 cm, 13 cm, 12 cm, and 8 cm, the perimeter P is calculated as:
| Side 1 | 9 cm |
| Side 2 | 10 cm |
| Side 3 | 14 cm |
| Side 4 | 13 cm |
| Side 5 | 12 cm |
| Side 6 | 8 cm |
| Total Perimeter (P) | 9 + 10 + 14 + 13 + 12 + 8 = 66 cm |
The formula for the perimeter of an irregular hexagon can be expressed as:
where \( s_i \) represents the length of each individual side of the hexagon.
Calculating the Perimeter with Given Side Length
The perimeter of a hexagon can be easily calculated if the side lengths are known. The process differs slightly for regular and irregular hexagons, but both methods are straightforward. Here's how to calculate the perimeter step by step:
Regular Hexagon
In a regular hexagon, all six sides are of equal length. The formula to find the perimeter \( P \) is:
\( P = 6s \)
where \( s \) is the length of one side. Simply multiply the side length by six.
- Step 1: Measure the length of one side of the hexagon.
- Step 2: Multiply this length by 6.
- Step 3: The result is the perimeter of the hexagon.
Example
Given a regular hexagon with a side length of 5 cm:
\( P = 6 \times 5 = 30 \) cm
Irregular Hexagon
For an irregular hexagon, where the sides can have different lengths, the perimeter is the sum of the lengths of all sides:
\( P = s_1 + s_2 + s_3 + s_4 + s_5 + s_6 \)
where \( s_1, s_2, s_3, s_4, s_5, s_6 \) are the lengths of the six sides.
- Step 1: Measure the length of each side of the hexagon.
- Step 2: Add all these lengths together.
- Step 3: The result is the perimeter of the hexagon.
Example
Given an irregular hexagon with side lengths of 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, and 8 cm:
\( P = 3 + 4 + 5 + 6 + 7 + 8 = 33 \) cm
Using these methods, you can easily determine the perimeter of any hexagon, whether regular or irregular, by applying the appropriate formula.
Calculating the Perimeter with Given Area
To calculate the perimeter of a regular hexagon when the area is given, you can follow these steps:
- First, recall the formula for the area of a regular hexagon:
where s is the side length of the hexagon. - Solve for the side length s. Given the area, rearrange the formula to find s:
Thus, s is:
- Calculate the perimeter. Once you have the side length, the perimeter P of the hexagon is:
Here is a step-by-step example:
- Suppose the area of a regular hexagon is 54 square units.
- Using the area formula, solve for s:
- Rearrange to solve for s:
- Calculate s:
- Finally, calculate the perimeter:
Calculating the Perimeter with Coordinates of Vertices
To calculate the perimeter of a hexagon when the coordinates of its vertices are given, you can use the distance formula to find the length of each side. The distance formula for two points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Here are the steps to follow:
- Identify the coordinates of the vertices: List the coordinates of all six vertices of the hexagon in order.
- Calculate the distance between consecutive vertices: Use the distance formula to calculate the length of each side. For a hexagon with vertices A, B, C, D, E, and F:
- \(AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} \)
- \(BC = \sqrt{(x_C - x_B)^2 + (y_C - y_B)^2} \)
- \(CD = \sqrt{(x_D - x_C)^2 + (y_D - y_C)^2} \)
- \(DE = \sqrt{(x_E - x_D)^2 + (y_E - y_D)^2} \)
- \(EF = \sqrt{(x_F - x_E)^2 + (y_F - y_E)^2} \)
- \(FA = \sqrt{(x_A - x_F)^2 + (y_A - y_F)^2} \)
- Sum the distances: Add all the calculated distances to find the perimeter of the hexagon.
\[
\text{Perimeter} = AB + BC + CD + DE + EF + FA
\]
Here is an example:
Given the vertices of a hexagon: A(0, 0), B(0, 4), C(3, 7), D(6, 4), E(6, 0), F(3, -3).
- Calculate each side length:
- \(AB = \sqrt{(0 - 0)^2 + (4 - 0)^2} = \sqrt{16} = 4\)
- \(BC = \sqrt{(3 - 0)^2 + (7 - 4)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24\)
- \(CD = \sqrt{(6 - 3)^2 + (4 - 7)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24\)
- \(DE = \sqrt{(6 - 6)^2 + (0 - 4)^2} = \sqrt{16} = 4\)
- \(EF = \sqrt{(3 - 6)^2 + ( -3 - 0)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24\)
- \(FA = \sqrt{(3 - 0)^2 + (-3 - 0)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24\)
- Sum the side lengths:
\[
\text{Perimeter} \approx 4 + 4.24 + 4.24 + 4 + 4.24 + 4.24 = 24.96
\]
Hexagons Inscribed in Circles
A hexagon inscribed in a circle is a special type of hexagon where all six vertices of the hexagon lie on the circumference of the circle. This setup provides a unique relationship between the hexagon and the circle, which can be used to easily calculate various properties of the hexagon, including its perimeter.
Properties of an Inscribed Hexagon
- All vertices of the hexagon lie on the circle.
- The center of the hexagon coincides with the center of the circle.
- The radius of the circle is equal to the distance from the center to any vertex of the hexagon.
- Each side of a regular hexagon inscribed in a circle is equal to the radius of the circle.
Calculating the Perimeter of an Inscribed Hexagon
To calculate the perimeter of a regular hexagon inscribed in a circle, follow these steps:
- Identify the radius (r) of the circle.
- Since each side of the hexagon is equal to the radius, the length of one side (s) is given by s = r.
- The perimeter (P) of the hexagon is the sum of the lengths of all its sides. Since a hexagon has six sides, the formula for the perimeter is:
\[ P = 6 \times r \]
Here's an example:
- If the radius of the circle is 5 cm, then the side length of the hexagon is also 5 cm.
- Using the formula for the perimeter:
\[ P = 6 \times 5 = 30 \, \text{cm} \]
Thus, the perimeter of the hexagon is 30 cm.
Visualization
Consider the following diagram to better understand the relationship between the hexagon and the circle:
 |
This diagram shows a regular hexagon perfectly inscribed in a circle, illustrating that each vertex touches the circle's circumference, and each side of the hexagon is equal to the radius of the circle.
Conclusion
Understanding the properties and relationships of a hexagon inscribed in a circle allows for straightforward calculations of its perimeter. By knowing the radius of the circumscribing circle, you can easily determine the side lengths and, consequently, the perimeter of the hexagon.
Real-life Applications
Hexagons are found extensively in nature and human-made structures due to their efficient and aesthetically pleasing properties. Here are some notable real-life applications:
- Natural Formations
- Beehives: Bees construct their hives using hexagonal cells. This structure allows them to maximize space and minimize the amount of wax needed.
- Snowflakes: Snowflakes often form hexagonal structures due to the molecular arrangement of water as it freezes, leading to unique and intricate designs.
- Insect Eyes: Many insects, such as dragonflies, have compound eyes made up of thousands of hexagonal lenses, providing a wide field of vision.
- Architecture and Engineering
- Tiling and Flooring: Hexagonal tiles are popular in tiling floors and walls because they can cover a surface without leaving gaps.
- Structural Efficiency: Hexagonal shapes are used in various structures, such as carbon nanotubes and graphene sheets, due to their strength and stability.
- Urban Planning: Some cities utilize hexagonal street grids to optimize space and traffic flow.
- Chemistry
- Benzene Molecules: The chemical structure of benzene consists of a hexagonal ring, which is a fundamental component in organic chemistry.
- Molecular Structures: Many organic compounds and complex molecules, such as glucose and DNA, feature hexagonal patterns.
- Technology and Design
- Graphical Representation: Hexagonal grids are used in computer graphics and gaming to create more natural and flexible spatial layouts.
- Satellite Technology: The James Webb Space Telescope features a hexagonal mirror array to optimize the collection of light.
Hexagons offer a blend of efficiency, strength, and beauty, making them a preferred shape in many natural and engineered systems.
Solved Examples
Here are some solved examples to help you understand how to calculate the perimeter of both regular and irregular hexagons:
Example 1: Regular Hexagon
Calculate the perimeter of a regular hexagon whose side length is 10 cm.
Solution:
- Identify the formula for the perimeter of a regular hexagon: \( P = 6s \), where \( s \) is the side length.
- Substitute the given side length into the formula: \( P = 6 \times 10 \).
- Calculate the result: \( P = 60 \) cm.
Thus, the perimeter of the regular hexagon is 60 cm.
Example 2: Irregular Hexagon
Calculate the perimeter of an irregular hexagon with side lengths of 5 cm, 6 cm, 7 cm, 8 cm, 9 cm, and 10 cm.
Solution:
- List the side lengths: 5 cm, 6 cm, 7 cm, 8 cm, 9 cm, 10 cm.
- Sum the lengths of all the sides: \( 5 + 6 + 7 + 8 + 9 + 10 \).
- Calculate the result: \( P = 45 \) cm.
Thus, the perimeter of the irregular hexagon is 45 cm.
Example 3: Hexagon Inscribed in a Circle
Calculate the perimeter of a regular hexagon inscribed in a circle with a radius of 4 units.
Solution:
- For a hexagon inscribed in a circle, the side length \( s \) equals the radius \( r \) of the circle.
- Use the formula for the perimeter of a regular hexagon: \( P = 6r \).
- Substitute the radius into the formula: \( P = 6 \times 4 \).
- Calculate the result: \( P = 24 \) units.
Thus, the perimeter of the inscribed hexagon is 24 units.
Example 4: Hexagon with Vertices Coordinates
Given the vertices of a hexagon at coordinates (1,1), (4,1), (5,4), (4,7), (1,7), and (0,4), calculate the perimeter.
Solution:
- Use the distance formula to find the length of each side: \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Calculate each side length:
- \( \overline{AB} = \sqrt{(4-1)^2 + (1-1)^2} = \sqrt{9} = 3 \) units
- \( \overline{BC} = \sqrt{(5-4)^2 + (4-1)^2} = \sqrt{1 + 9} = \sqrt{10} \) units
- \( \overline{CD} = \sqrt{(4-5)^2 + (7-4)^2} = \sqrt{1 + 9} = \sqrt{10} \) units
- \( \overline{DE} = \sqrt{(1-4)^2 + (7-7)^2} = \sqrt{9} = 3 \) units
- \( \overline{EF} = \sqrt{(0-1)^2 + (4-7)^2} = \sqrt{1 + 9} = \sqrt{10} \) units
- \( \overline{FA} = \sqrt{(1-0)^2 + (1-4)^2} = \sqrt{1 + 9} = \sqrt{10} \) units
- Sum the lengths of all sides: \( 3 + \sqrt{10} + \sqrt{10} + 3 + \sqrt{10} + \sqrt{10} \).
- Simplify the result: \( P = 6 + 4\sqrt{10} \) units.
Thus, the perimeter of the hexagon with the given vertices is \( 6 + 4\sqrt{10} \) units.
Practice Problems
Below are some practice problems to help you understand and calculate the perimeter of a hexagon. Try solving these problems step by step, and check your answers at the end.
-
Problem 1: Find the perimeter of a regular hexagon where each side is 7 cm long.
Solution:
- Since it's a regular hexagon, all sides are equal.
- Perimeter \( P \) = 6 × side length
- \( P = 6 \times 7 \, \text{cm} = 42 \, \text{cm} \)
-
Problem 2: Calculate the perimeter of an irregular hexagon with sides measuring 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, and 9 cm.
Solution:
- Perimeter \( P \) = Sum of all side lengths
- \( P = 4 \, \text{cm} + 5 \, \text{cm} + 6 \, \text{cm} + 7 \, \text{cm} + 8 \, \text{cm} + 9 \, \text{cm} \)
- \( P = 39 \, \text{cm} \)
-
Problem 3: The perimeter of a regular hexagon is 54 cm. What is the length of each side?
Solution:
- Perimeter \( P \) = 6 × side length
- Given \( P = 54 \, \text{cm} \)
- Side length \( s = \frac{P}{6} = \frac{54 \, \text{cm}}{6} = 9 \, \text{cm} \)
-
Problem 4: A hexagon has vertices at the coordinates (0,0), (2,3), (4,3), (6,0), (4,-3), and (2,-3). Find the perimeter of the hexagon.
Solution:
- Calculate the distance between each pair of adjacent vertices using the distance formula:
- Distance \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Sum the distances to find the perimeter:
- \( d_1 = \sqrt{(2-0)^2 + (3-0)^2} = \sqrt{4 + 9} = \sqrt{13} \)
- \( d_2 = \sqrt{(4-2)^2 + (3-3)^2} = \sqrt{4} = 2 \)
- \( d_3 = \sqrt{(6-4)^2 + (0-3)^2} = \sqrt{4 + 9} = \sqrt{13} \)
- \( d_4 = \sqrt{(4-6)^2 + (-3-0)^2} = \sqrt{4 + 9} = \sqrt{13} \)
- \( d_5 = \sqrt{(2-4)^2 + (-3--3)^2} = \sqrt{4} = 2 \)
- \( d_6 = \sqrt{(0-2)^2 + (0--3)^2} = \sqrt{4 + 9} = \sqrt{13} \)
- Perimeter \( P = \sqrt{13} + 2 + \sqrt{13} + \sqrt{13} + 2 + \sqrt{13} = 4\sqrt{13} + 4 \approx 20.48 \, \text{units} \)
-
Problem 5: Each side of a regular hexagon is \( x \) units long. Write an expression for the perimeter of the hexagon and calculate it for \( x = 5 \, \text{units} \).
Solution:
- Perimeter \( P = 6 \times x \)
- For \( x = 5 \, \text{units} \):
- \( P = 6 \times 5 \, \text{units} = 30 \, \text{units} \)

Common Mistakes and Tips
When calculating the perimeter of a hexagon, it's essential to avoid common mistakes to ensure accuracy. Here are some common pitfalls and tips to help you calculate the perimeter correctly:
Common Mistakes
- Assuming a Hexagon is Regular: The formula \( P = 6s \) (where \( s \) is the side length) only applies to regular hexagons. Always verify that all six sides are equal before using this formula.
- Mixing Units: Ensure all measurements are in the same unit. Mixing units (e.g., centimeters and inches) can lead to incorrect calculations.
- Rounding Off Too Early: Keep your precision until the final step. Rounding intermediate values can introduce errors in your final result.
- Confusing Apothem with Side Length: The apothem is a perpendicular line from the center to a side. Do not confuse this with the side length, as the perimeter calculation requires the side length.
Tips for Accurate Calculation
- Double-Check Measurements: Before performing any calculations, double-check that all side lengths are measured accurately and consistently.
- Use Appropriate Tools: Utilize geometry tools such as rulers and protractors for precise measurements. For complex calculations, consider using a calculator or geometry software.
- Verify Regularity: For regular hexagons, ensure all sides and angles are equal. For irregular hexagons, accurately sum the lengths of all sides.
- Utilize Online Resources: Online calculators and math software can help verify your results and provide quick and accurate calculations.
Example Problem
Consider a regular hexagon with a side length of 5 cm. To find the perimeter:
- Verify that it is a regular hexagon (all sides are equal).
- Use the formula for the perimeter of a regular hexagon: \( P = 6s \).
- Substitute the side length: \( P = 6 \times 5 \, \text{cm} = 30 \, \text{cm} \).
- Write the final answer with the correct units: The perimeter is 30 cm.
Advanced Tip
For hexagons inscribed in circles, remember that the side length can be found using the radius of the circumscribed circle. If the radius \( R \) is known, the side length \( s \) of the regular hexagon is given by:
\[
s = R \sqrt{3}
\]
Then, use \( P = 6s \) to find the perimeter.
Conclusion
In conclusion, finding the perimeter of a hexagon is a straightforward task once you understand the type of hexagon you are working with. For a regular hexagon, the perimeter can be easily calculated by multiplying the side length by six, since all sides are equal. In the case of an irregular hexagon, the perimeter is the sum of the lengths of all six sides.
Understanding the different methods to calculate the perimeter, whether using side lengths, coordinates, or geometric properties, is essential for solving various real-life problems and applications. Hexagons are prevalent in nature and human-made structures, making this knowledge both practical and valuable.
By practicing with different examples and being aware of common mistakes, you can become proficient in calculating the perimeter of any hexagon, ensuring accuracy in your mathematical endeavors. Remember, attention to detail and a clear understanding of the properties of hexagons are key to mastering this concept.
Overall, mastering the calculation of a hexagon's perimeter enhances your geometric problem-solving skills and allows you to appreciate the mathematical beauty and utility of hexagonal shapes in various contexts.
Chu vi của Lục giác đều: Bài toán trong ngày