Topic parallelogram perimeter and area: Discover the secrets to calculating the perimeter and area of a parallelogram with ease. This comprehensive guide provides clear explanations, step-by-step instructions, and practical examples to help you master these essential geometry concepts. Perfect for students, teachers, and anyone looking to enhance their math skills.
Table of Content
- Perimeter and Area of a Parallelogram
- Introduction to Parallelograms
- Properties of Parallelograms
- Understanding the Perimeter of a Parallelogram
- Calculating the Perimeter: Step-by-Step Guide
- Understanding the Area of a Parallelogram
- Calculating the Area: Step-by-Step Guide
- Formulas for Perimeter and Area
- Examples and Practice Problems
- Common Mistakes to Avoid
- Applications of Parallelogram in Real Life
- Advanced Topics: Special Types of Parallelograms
- Summary and Key Takeaways
- Frequently Asked Questions (FAQs)
- YOUTUBE: Video này hướng dẫn cách tính diện tích và chu vi của hình bình hành, giúp bạn nắm vững các công thức và áp dụng vào thực tế.
Perimeter and Area of a Parallelogram
A parallelogram is a four-sided figure with opposite sides that are equal and parallel. Calculating the perimeter and area of a parallelogram involves understanding its base, height, and sides.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around the outside of the figure. To find the perimeter, you need to know the lengths of its sides.
The formula for the perimeter \(P\) of a parallelogram is:
\[ P = 2(a + b) \]
where \(a\) and \(b\) are the lengths of the two pairs of parallel sides.
Area of a Parallelogram
The area of a parallelogram is the space contained within its sides. To find the area, you need to know the base and the height (the perpendicular distance between the bases).
The formula for the area \(A\) of a parallelogram is:
\[ A = b \times h \]
where \(b\) is the length of the base and \(h\) is the height.
Examples
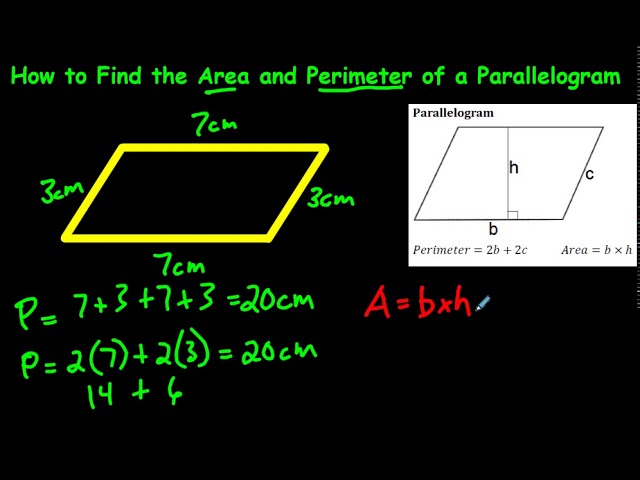
- Example 1: If a parallelogram has sides of length 5 cm and 8 cm, the perimeter is calculated as:
\[ P = 2(5 + 8) = 2 \times 13 = 26 \text{ cm} \] - Example 2: If the base of a parallelogram is 10 cm and the height is 7 cm, the area is calculated as:
\[ A = 10 \times 7 = 70 \text{ cm}^2 \]
Properties of a Parallelogram
- Opposite sides are equal in length.
- Opposite angles are equal in measure.
- Adjacent angles are supplementary (add up to 180 degrees).
- The diagonals bisect each other.
Key Takeaways
- The perimeter of a parallelogram depends on the lengths of its sides.
- The area of a parallelogram is determined by its base and height.
- Understanding the properties of parallelograms can help in solving related geometric problems.
READ MORE:
Introduction to Parallelograms
A parallelogram is a four-sided polygon, or quadrilateral, with opposite sides that are both equal in length and parallel. This geometric shape has several unique properties that make it an important topic in geometry. Parallelograms can appear in various forms, including rectangles, rhombuses, and squares, which are all special types of parallelograms.
Here are some fundamental properties of parallelograms:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- Adjacent angles are supplementary, meaning they add up to 180 degrees.
- The diagonals of a parallelogram bisect each other.
Parallelograms are classified into different types based on their side lengths and angles:
- Rectangle: A parallelogram with four right angles.
- Rhombus: A parallelogram with all sides of equal length.
- Square: A parallelogram with all sides of equal length and four right angles.
Understanding the properties of parallelograms is essential for solving problems related to their perimeter and area. These properties also help in identifying and differentiating parallelograms from other quadrilaterals.
In the following sections, we will explore how to calculate the perimeter and area of a parallelogram, providing you with the tools and knowledge to master these fundamental geometric concepts.
Properties of Parallelograms
Parallelograms have several distinctive properties that differentiate them from other quadrilaterals. These properties are crucial for understanding and solving geometric problems involving parallelograms. Below are the key properties of parallelograms:
- Opposite Sides are Equal and Parallel: In a parallelogram, both pairs of opposite sides are equal in length and parallel to each other. If \(ABCD\) is a parallelogram, then \(AB = CD\) and \(AD = BC\).
- Opposite Angles are Equal: The angles opposite to each other in a parallelogram are equal. Thus, \(\angle A = \angle C\) and \(\angle B = \angle D\).
- Adjacent Angles are Supplementary: Any two adjacent angles in a parallelogram add up to 180 degrees. For example, \(\angle A + \angle B = 180^\circ\).
- Diagonals Bisect Each Other: The diagonals of a parallelogram bisect each other. This means that each diagonal cuts the other into two equal parts. If \(AC\) and \(BD\) are diagonals, then \(AO = OC\) and \(BO = OD\), where \(O\) is the point of intersection.
These properties can be summarized in the following table:
| Property | Description |
| Opposite Sides | Equal and Parallel |
| Opposite Angles | Equal |
| Adjacent Angles | Supplementary (add up to 180 degrees) |
| Diagonals | Bisect each other |
These inherent properties not only define parallelograms but also provide the foundation for further exploration into their perimeter and area calculations, which will be covered in subsequent sections.
Understanding the Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around its edges. This can be calculated easily because opposite sides of a parallelogram are equal in length. Therefore, if you know the lengths of two adjacent sides, you can determine the perimeter using the formula:
- Let the lengths of the adjacent sides be denoted as a and b.
- The formula to calculate the perimeter (P) is:
\[
P = 2(a + b)
\]
Here's a step-by-step guide to finding the perimeter:
- Measure the lengths of the adjacent sides of the parallelogram.
- Add these two lengths together.
- Multiply the sum by 2 to get the perimeter.
For example, if a parallelogram has side lengths of 8 cm and 12 cm, the perimeter is calculated as follows:
\[
P = 2(a + b) = 2(8 \, \text{cm} + 12 \, \text{cm}) = 2 \times 20 \, \text{cm} = 40 \, \text{cm}
\]
Sometimes, you might not know the lengths of both pairs of sides directly, but you can still find the perimeter if you have the necessary information, such as one side length and the lengths of the diagonals. In this case, you can use the law of cosines and additional geometric properties to find the unknown side length and then apply the standard perimeter formula.
For instance, if a parallelogram has one side of length 7 cm and diagonals of lengths 9 cm and 11 cm, the perimeter can be calculated using derived formulas involving these diagonals. However, the general approach is to rely on the simpler and more direct formula wherever possible.
Calculating the Perimeter: Step-by-Step Guide
The perimeter of a parallelogram is the total distance around its edges. To find the perimeter, you need to know the lengths of the base and the side. The perimeter can be calculated using the formula:
\[ P = 2(a + b) \]
where \(a\) is the length of the base and \(b\) is the length of the side.
Step-by-Step Guide:
-
Identify the lengths of the sides:
Measure or identify the lengths of the base (\(a\)) and the side (\(b\)). Ensure both measurements are in the same units.
-
Apply the perimeter formula:
Substitute the values of \(a\) and \(b\) into the formula:
\[ P = 2(a + b) \]
-
Calculate the sum inside the parentheses:
Add the lengths of the base and the side:
\[ a + b \]
-
Multiply by 2:
Multiply the sum by 2 to find the perimeter:
\[ P = 2(a + b) \]
Example:
Let's calculate the perimeter of a parallelogram with a base length of 12 cm and a side length of 8 cm.
-
Identify the lengths: \(a = 12\) cm and \(b = 8\) cm.
-
Apply the formula: \( P = 2(12 + 8) \).
-
Calculate the sum: \( 12 + 8 = 20 \).
-
Multiply by 2: \( P = 2 \times 20 = 40 \) cm.
Therefore, the perimeter of the parallelogram is 40 cm.
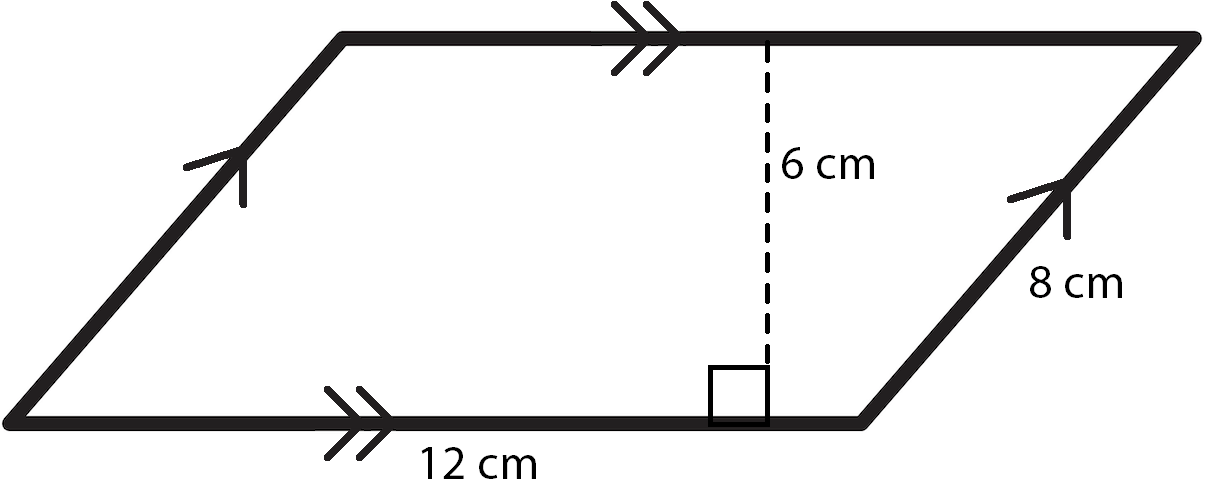
Understanding the Area of a Parallelogram
The area of a parallelogram is a measure of the space contained within its boundaries. To understand how to calculate the area, it is essential to recognize the key components of a parallelogram: the base and the height.
Basic Formula for Area
The most straightforward formula for the area of a parallelogram is:
where:
b is the length of the baseh is the height, which is the perpendicular distance from the base to the opposite side
Step-by-Step Calculation
- Identify the base (
b ) of the parallelogram. This can be any one of its sides. - Determine the height (
h ). This is the perpendicular distance from the chosen base to the opposite side. If the height is not given, it may need to be calculated or measured. - Multiply the base by the height to find the area.
Example Calculation
Consider a parallelogram with a base of 8 cm and a height of 5 cm. The area is calculated as follows:
Alternative Formula Using Trigonometry
If the lengths of two adjacent sides and the included angle are known, the area can also be calculated using the formula:
where:
a andb are the lengths of the adjacent sides\theta is the included angle between these sides
This formula uses the sine of the included angle to determine the height indirectly.
Example Calculation Using Trigonometry
For a parallelogram with sides of lengths 7 cm and 10 cm and an included angle of 60 degrees, the area can be calculated as:
Using a Grid to Approximate Area
Another method to approximate the area of a parallelogram is to count the number of unit squares it covers on a grid. This method is useful for visualizing and understanding the concept of area.
By following these methods, the area of a parallelogram can be accurately determined, providing a fundamental understanding of this geometric concept.
Calculating the Area: Step-by-Step Guide
To calculate the area of a parallelogram, you need to know the base and the height. The base is one of the sides of the parallelogram, and the height is the perpendicular distance from the base to the opposite side.
- Identify the Base and Height
First, identify the base (b) and the height (h) of the parallelogram. The base is any one of its sides, and the height is the perpendicular distance from the base to the opposite side.
- Apply the Area Formula
The formula for the area (A) of a parallelogram is:
\[ A = b \times h \]
Here, \( b \) is the base and \( h \) is the height.
- Example Calculation
Suppose the base of a parallelogram is 6 cm, and the height is 4 cm. Using the formula, we get:
\[ A = 6 \, \text{cm} \times 4 \, \text{cm} = 24 \, \text{cm}^2 \]
- Using Different Measurements
If the height is not given, you can use trigonometry to find it. Suppose you know the length of the sides and one angle between them. Let \( a \) and \( b \) be the sides, and \( \theta \) the angle between them. The height can be found using:
\[ h = a \sin(\theta) \]
Then, use the area formula:
\[ A = b \times (a \sin(\theta)) \]
- Area Using Diagonals
If the lengths of the diagonals \( d_1 \) and \( d_2 \) and the angle \( \theta \) between them are known, the area can also be calculated using:
\[ A = \frac{1}{2} d_1 d_2 \sin(\theta) \]
These methods ensure you can find the area of any parallelogram as long as you have the necessary measurements.
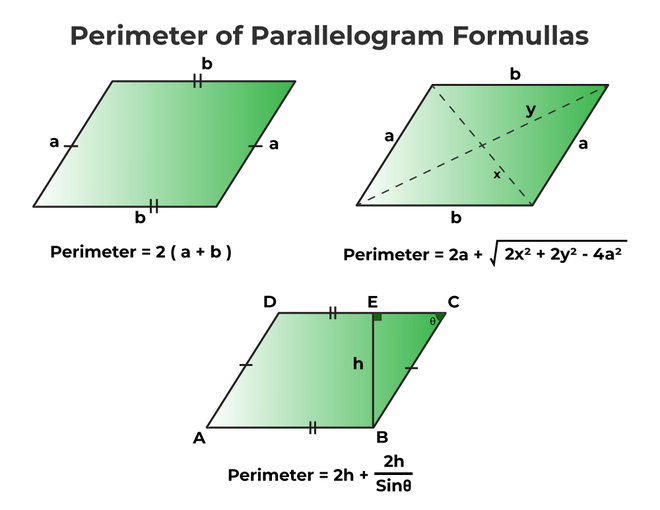
Formulas for Perimeter and Area
Parallelograms have distinct formulas to calculate their perimeter and area. Understanding these formulas is essential for solving various geometry problems related to parallelograms.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around its edges. Since the opposite sides of a parallelogram are equal in length, the perimeter can be calculated using the lengths of any two adjacent sides.
The formula for the perimeter (P) is:
\[
P = 2(a + b)
\]
where \(a\) and \(b\) are the lengths of the adjacent sides of the parallelogram.
Example:
- If a parallelogram has sides of length 8 cm and 5 cm, the perimeter is calculated as:
\[
P = 2(8 + 5) = 2 \times 13 = 26 \text{ cm}
\]
Area of a Parallelogram
The area of a parallelogram is the amount of space enclosed within its sides. The most common way to calculate the area is by using the base and height of the parallelogram.
The formula for the area (A) is:
\[
A = b \times h
\]
where \(b\) is the length of the base and \(h\) is the height (the perpendicular distance between the bases).
Example:
- If a parallelogram has a base of 10 cm and a height of 6 cm, the area is:
\[
A = 10 \times 6 = 60 \text{ cm}^2
\]
Alternate Area Formula
Another method to calculate the area involves the lengths of two adjacent sides and the sine of the included angle. This formula is particularly useful when the height is not directly known.
The formula is:
\[
A = a \times b \times \sin(\theta)
\]
where \(a\) and \(b\) are the lengths of the adjacent sides, and \(\theta\) is the angle between them.
Example:
- If a parallelogram has sides of length 7 cm and 9 cm, with an included angle of 60 degrees, the area is:
\[
A = 7 \times 9 \times \sin(60^\circ) \approx 7 \times 9 \times 0.866 \approx 54.7 \text{ cm}^2
\]
Examples and Practice Problems
Here are some examples and practice problems to help you understand how to calculate the perimeter and area of a parallelogram.
Example 1: Finding the Area
A parallelogram has a base of 12 feet and a height of 11 feet. Find the area.
Solution:
- Base, \( b = 12 \) feet
- Height, \( h = 11 \) feet
Using the formula for the area:
\[ A = b \times h \]
\[ A = 12 \times 11 \]
\[ A = 132 \, \text{square feet} \]
Therefore, the area of the parallelogram is 132 square feet.
Example 2: Finding the Perimeter
A parallelogram has sides of 15 yards and 17 yards. Find the perimeter.
Solution:
- Side 1, \( a = 15 \) yards
- Side 2, \( b = 17 \) yards
Using the formula for the perimeter:
\[ P = 2(a + b) \]
\[ P = 2(15 + 17) \]
\[ P = 2(32) \]
\[ P = 64 \, \text{yards} \]
Therefore, the perimeter of the parallelogram is 64 yards.
Practice Problems
-
Find the perimeter of a parallelogram with adjacent sides of 15 meters and 25 meters.
- 40 meters
- 80 meters
- 55 meters
- 60 meters
Answer: 80 meters
-
Find the area of a parallelogram with a base of 10 yards and a height of 6 yards.
Answer: 60 square yards
-
Calculate the area of a parallelogram whose diagonals are 15 units and 20 units, and the angle of intersection between the diagonals is 30°.
Answer: 75 square units
-
Which of the following is not a parallelogram?
- Rhombus
- Rectangle
- Square
- Trapezium
Answer: Trapezium
Common Mistakes to Avoid
When calculating the perimeter and area of a parallelogram, several common mistakes can occur. Understanding these mistakes can help ensure accurate results and a deeper comprehension of the concepts involved. Below are some common mistakes and how to avoid them:
-
Confusing Base and Height with Sides:
The base and height of a parallelogram are perpendicular to each other, but they are not necessarily the sides of the parallelogram. Always ensure you identify the correct base and height for area calculations.
-
Incorrect Use of Formulas:
Using the wrong formula for the perimeter or area is a frequent error. The perimeter formula is \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of adjacent sides. The area formula is \( A = b \times h \), where \( b \) is the base and \( h \) is the height.
-
Misinterpreting Diagonals and Angles:
Sometimes, problems provide the lengths of diagonals or angles. Ensure you understand how these relate to the sides and use the correct relationships and trigonometric functions if needed.
-
Assuming All Angles are Right Angles:
Unlike rectangles, parallelograms do not necessarily have right angles. Do not assume right angles unless explicitly stated.
-
Ignoring Units:
Make sure all measurements are in the same unit before performing calculations. Mixing units can lead to incorrect results.
-
Overlooking the Properties of Parallelograms:
Remember the key properties: opposite sides are equal, opposite angles are equal, and the diagonals bisect each other. These properties can help verify calculations.
-
Incorrectly Applying Trigonometric Functions:
When dealing with angles, ensure you use the correct trigonometric functions and understand the relationships between sides and angles.
By being mindful of these common mistakes and verifying each step of your calculations, you can achieve accurate and reliable results when working with the perimeter and area of parallelograms.
Applications of Parallelogram in Real Life
Parallelograms are not just theoretical geometric shapes; they have numerous practical applications in various fields. Here are some key examples:
-
Architecture and Construction:
Many buildings and structures incorporate parallelograms in their design to ensure stability and aesthetic appeal. For instance, the Dockland Office Building in Hamburg, Germany, is a notable example where the structure follows the form of a parallelogram.
-
Engineering:
Parallelograms are used in mechanical engineering to transfer motion efficiently. Devices like pantographs, which are used to copy and scale drawings, rely on parallelogram structures to maintain the correct proportions.
-
Roof Designs:
Gable roofs, saltbox roofs, and shed roofs often exhibit parallelogram shapes when viewed from the side. This design helps distribute the weight evenly, providing structural stability.
-
Sports Fields:
Many sports fields, such as basketball and tennis courts, are laid out in parallelogram shapes to maximize the use of space and ensure even boundaries.
-
Solar Panels:
Solar panels are often designed in parallelogram shapes to fit efficiently on various types of roofs, optimizing space and sunlight capture.
-
Everyday Objects:
Common items like notebooks, smartphones, and keyboards often take the shape of parallelograms, making them functional and easy to use.
-
Textile Design:
Parallelogram patterns are frequently used in textiles, such as cardigans and sweaters, for their aesthetic appeal and ease of production in knitting and weaving.
-
Crafts:
Craft sheets often come in parallelogram shapes, which are popular in various handicrafts and DIY projects due to their versatility.
These examples highlight how the properties of parallelograms—such as parallel sides, equal lengths, and congruent angles—are utilized to create functional and aesthetically pleasing designs in everyday life and specialized fields.
Advanced Topics: Special Types of Parallelograms
Special types of parallelograms include the rectangle, rhombus, and square. Each of these shapes has unique properties that distinguish them from the general category of parallelograms.
Rectangle
A rectangle is a parallelogram with four right angles. This implies that every angle in a rectangle is 90 degrees.
- Opposite sides are equal and parallel.
- Diagonals are equal in length and bisect each other.
- It has two lines of symmetry: horizontal and vertical.
Formulas:
- Area: \(A = l \times w\)
- Perimeter: \(P = 2(l + w)\)
- Diagonal: \(d = \sqrt{l^2 + w^2}\)
Rhombus
A rhombus is a parallelogram with all four sides of equal length.
- Opposite sides are parallel and opposite angles are equal.
- Diagonals bisect each other at right angles and bisect opposite angles.
- Each diagonal divides the rhombus into two congruent triangles.
Formulas:
- Area: \(A = \frac{1}{2} \times d_1 \times d_2\)
- Perimeter: \(P = 4a\)
Square
A square is a parallelogram with all four sides equal and all angles equal to 90 degrees.
- It is both equilateral (all sides equal) and equiangular (all angles equal).
- Diagonals are equal, bisect each other at right angles, and bisect the angles of the square.
- It has four lines of symmetry: two diagonals, one horizontal, and one vertical.
Formulas:
- Area: \(A = a^2\)
- Perimeter: \(P = 4a\)
- Diagonal: \(d = a\sqrt{2}\)
Summary and Key Takeaways
Understanding the perimeter and area of a parallelogram is fundamental in geometry. Here are the key points and formulas to remember:
-
Definition and Properties:
- A parallelogram is a quadrilateral with opposite sides parallel and equal in length.
- Opposite angles are equal, and adjacent angles are supplementary.
- The diagonals bisect each other.
-
Formulas:
- Perimeter: \(P = 2(a + b)\), where \(a\) and \(b\) are the lengths of adjacent sides.
- Area: \(A = b \times h\), where \(b\) is the base and \(h\) is the height.
- Alternative area formulas:
- Using two sides and the included angle: \(A = ab \sin(\theta)\).
- Using diagonals and the angle between them: \(A = \frac{1}{2} \times d_1 \times d_2 \sin(\alpha)\).
-
Steps for Calculation:
- Identify the given dimensions (base, height, sides, angles, or diagonals).
- Choose the appropriate formula based on the given data.
- Substitute the values into the formula and solve for the required quantity (perimeter or area).
-
Common Mistakes to Avoid:
- Confusing the base with the height or using the slant height instead of the perpendicular height.
- Incorrectly calculating angles or misapplying trigonometric functions.
- Neglecting to convert units to a common measure before performing calculations.
-
Applications:
- Parallelograms are used in engineering and architecture for structural designs.
- They appear in various real-life objects, such as tiles, patterns, and artworks.
By mastering these concepts and formulas, you will be well-equipped to solve a wide range of problems involving parallelograms. Practice with different examples to reinforce your understanding and improve your skills.
Frequently Asked Questions (FAQs)
-
What is a parallelogram?
A parallelogram is a type of quadrilateral where both pairs of opposite sides are parallel and equal in length.
-
What is the formula for the perimeter of a parallelogram?
The perimeter of a parallelogram is calculated using the formula \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of adjacent sides.
-
How do you calculate the area of a parallelogram?
The area of a parallelogram is given by the formula \( A = b \cdot h \), where \( b \) is the base and \( h \) is the height perpendicular to the base.
-
What are the properties of a parallelogram?
The properties of a parallelogram include:
- Opposite sides are parallel and equal.
- Opposite angles are equal.
- Consecutive angles are supplementary.
- The diagonals bisect each other.
-
What are some real-life examples of parallelograms?Common real-life examples of parallelograms include the faces of a brick, certain styles of floor tiles, and the layout of some buildings and bridges.
-
How is a parallelogram different from other quadrilaterals?
Unlike other quadrilaterals, a parallelogram has the unique property where both pairs of opposite sides are parallel and equal in length, which is not necessarily true for other quadrilaterals like trapezoids or general quadrilaterals.
-
Can a square be considered a parallelogram?
Yes, a square is a special type of parallelogram where all sides are equal and all angles are right angles.
-
What is the significance of the diagonals in a parallelogram?
The diagonals of a parallelogram bisect each other, meaning they cut each other exactly in half. This property is used in various geometric proofs and calculations.
-
How can you find the length of the diagonals in a parallelogram?
The length of the diagonals can be found using the properties of the parallelogram and the Pythagorean theorem. For instance, if you know the sides and one angle, you can apply trigonometric relationships to find the diagonals.
-
Are all parallelograms rectangles?
No, not all parallelograms are rectangles. While all rectangles are parallelograms (having parallel and equal opposite sides), parallelograms do not necessarily have all angles as right angles, which is a requirement for rectangles.
Video này hướng dẫn cách tính diện tích và chu vi của hình bình hành, giúp bạn nắm vững các công thức và áp dụng vào thực tế.
Cách Tính Diện Tích và Chu Vi Hình Bình Hành
READ MORE:
Học cách tính diện tích hình bình hành một cách dễ dàng và chính xác. Video này sẽ giúp bạn hiểu rõ hơn về cách tính diện tích hình bình hành và áp dụng vào bài tập thực tế.
Diện Tích Hình Bình Hành | Cách Tìm Diện Tích Hình Bình Hành