Topic perimeter and area of a triangle formula: Welcome to our comprehensive guide on the perimeter and area formulas of triangles. Whether you're a student looking to ace your exams or just curious about geometry, this article will provide clear explanations, step-by-step calculations, and real-life applications to enhance your understanding of these fundamental geometric concepts.
Table of Content
- Formulas for Perimeter and Area of a Triangle
- Introduction to Triangles
- Understanding Triangle Basics
- Types of Triangles
- Formula for Perimeter
- Examples of Perimeter Calculations
- Formula for Area using Base and Height
- Heron's Formula for Area
- Trigonometric Method for Area Calculation
- Coordinate Geometry Method for Area Calculation
- Examples of Area Calculations
- Applications of Triangle Formulas
- Real-life Applications
- Common Mistakes and Tips
- Advanced Topics
- Special Triangle Cases
- Additional Resources
- Conclusion
- YOUTUBE:
Formulas for Perimeter and Area of a Triangle
Triangles are fundamental shapes in geometry, and understanding their properties is essential. Here, we provide detailed formulas for calculating the perimeter and area of a triangle.
Perimeter of a Triangle
The perimeter of a triangle is the total length of its three sides. For a triangle with sides of lengths \(a\), \(b\), and \(c\), the formula is:
\[ \text{Perimeter} = a + b + c \]
Area of a Triangle
The area of a triangle can be calculated using various methods depending on the known parameters. Below are some commonly used formulas:
Using Base and Height
If the base (\(b\)) and height (\(h\)) of the triangle are known, the area is given by:
\[ \text{Area} = \frac{1}{2} \times b \times h \]
Using Heron's Formula
When the lengths of all three sides (\(a\), \(b\), and \(c\)) are known, Heron's formula can be used. First, calculate the semi-perimeter (\(s\)):
\[ s = \frac{a + b + c}{2} \]
Then, the area is given by:
\[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
Using Trigonometry
If two sides and the included angle are known, the area can be calculated using the sine function. For sides \(a\) and \(b\) with the included angle \(C\), the formula is:
\[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \]
Using Coordinates
For a triangle with vertices at coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area can be found using the determinant formula:
\[ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
Summary of Formulas
- Perimeter: \( P = a + b + c \)
- Area (Base and Height): \( A = \frac{1}{2} \times b \times h \)
- Area (Heron's Formula): \( A = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s = \frac{a + b + c}{2} \)
- Area (Trigonometry): \( A = \frac{1}{2} \times a \times b \times \sin(C) \)
- Area (Coordinates): \( A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \)

READ MORE:
Introduction to Triangles
Understanding Triangle Basics
Types of Triangles
Formula for Perimeter

Examples of Perimeter Calculations
Here are detailed examples of how to calculate the perimeter of different types of triangles:
Example 1: Equilateral Triangle
In an equilateral triangle, all three sides are of equal length. If each side measures 6 cm, the perimeter \(P\) is calculated as:
\[
P = a + a + a = 3a
\]
Substituting the value of \(a\):
\[
P = 3 \times 6 = 18 \text{ cm}
\]
Example 2: Isosceles Triangle
In an isosceles triangle, two sides are of equal length. If the equal sides each measure 5 cm and the base measures 8 cm, the perimeter \(P\) is calculated as:
\[
P = a + a + b = 2a + b
\]
Substituting the values:
\[
P = 2 \times 5 + 8 = 10 + 8 = 18 \text{ cm}
\]
Example 3: Scalene Triangle
In a scalene triangle, all sides are of different lengths. If the sides measure 7 cm, 8 cm, and 5 cm, the perimeter \(P\) is calculated as:
\[
P = a + b + c
\]
Substituting the values:
\[
P = 7 + 8 + 5 = 20 \text{ cm}
\]
Example 4: Right Triangle
In a right triangle, one angle is \(90^\circ\). If the two legs measure 3 cm and 4 cm, and the hypotenuse measures 5 cm, the perimeter \(P\) is calculated as:
\[
P = a + b + c
\]
Substituting the values:
\[
P = 3 + 4 + 5 = 12 \text{ cm}
\]
Example 5: Solving for a Missing Side
Given a triangle with a perimeter of 24 cm and two sides measuring 7 cm and 8 cm, we need to find the missing side \(x\). The perimeter equation is:
\[
P = a + b + c
\]
Given \(P = 24\), \(a = 7\), and \(b = 8\), solve for \(c\):
\[
24 = 7 + 8 + x
\]
\[
x = 24 - 15 = 9 \text{ cm}
\]
Formula for Area using Base and Height
The area of a triangle can be easily calculated if the base and the height are known. The formula is given by:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Below are some step-by-step examples to illustrate this formula:
-
Example 1: Find the area of a triangle with a base of 10 inches and a height of 5 inches.
Solution:
\[ \text{Area} = \frac{1}{2} \times 10 \, \text{inches} \times 5 \, \text{inches} \]
\[ \text{Area} = \frac{1}{2} \times 50 \, \text{square inches} \]
\[ \text{Area} = 25 \, \text{square inches} \]
-
Example 2: Calculate the area of a triangle with a base of 8 cm and a height of 7 cm.
Solution:
\[ \text{Area} = \frac{1}{2} \times 8 \, \text{cm} \times 7 \, \text{cm} \]
\[ \text{Area} = \frac{1}{2} \times 56 \, \text{square cm} \]
\[ \text{Area} = 28 \, \text{square cm} \]
-
Example 3: Determine the area of a triangle with a base of 15 meters and a height of 10 meters.
Solution:
\[ \text{Area} = \frac{1}{2} \times 15 \, \text{meters} \times 10 \, \text{meters} \]
\[ \text{Area} = \frac{1}{2} \times 150 \, \text{square meters} \]
\[ \text{Area} = 75 \, \text{square meters} \]
Heron's Formula for Area
Heron's Formula provides a method to calculate the area of a triangle when the lengths of all three sides are known. It is a two-step process:
-
Calculate the semi-perimeter \( s \):
\( s = \frac{a + b + c}{2} \) -
Use the semi-perimeter to find the area \( A \):
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)
Let's look at an example to understand the application of Heron's Formula:
-
Example: Find the area of a triangle with sides \( a = 7 \), \( b = 8 \), and \( c = 9 \).
-
Calculate the semi-perimeter \( s \):
\( s = \frac{7 + 8 + 9}{2} = 12 \) -
Use the semi-perimeter to find the area \( A \):
\( A = \sqrt{12(12-7)(12-8)(12-9)} \)
\( A = \sqrt{12 \times 5 \times 4 \times 3} \)
\( A = \sqrt{720} \)
\( A \approx 26.83 \, \text{square units} \)
-
Calculate the semi-perimeter \( s \):
-
Example: Find the area of a triangle with sides \( a = 10 \), \( b = 24 \), and \( c = 26 \).
-
Calculate the semi-perimeter \( s \):
\( s = \frac{10 + 24 + 26}{2} = 30 \) -
Use the semi-perimeter to find the area \( A \):
\( A = \sqrt{30(30-10)(30-24)(30-26)} \)
\( A = \sqrt{30 \times 20 \times 6 \times 4} \)
\( A = \sqrt{14400} \)
\( A = 120 \, \text{square units} \)
-
Calculate the semi-perimeter \( s \):
Heron's Formula is particularly useful for triangles where the height is not known, allowing for the area to be calculated solely from the side lengths.
Trigonometric Method for Area Calculation
The trigonometric method for calculating the area of a triangle uses the lengths of two sides and the included angle between them. This method is especially useful for non-right-angled triangles.
To calculate the area of a triangle using this method, follow these steps:
- Identify the lengths of two sides of the triangle and the measure of the included angle.
- Use the formula: \[ \text{Area} = \frac{1}{2} \cdot a \cdot b \cdot \sin(C) \] where \(a\) and \(b\) are the lengths of the sides, and \(C\) is the included angle.
- Substitute the known values into the formula and compute the result.
Here are some examples to illustrate the method:
- Example 1:
- Given: \(a = 7\), \(b = 10\), and \(C = 25^\circ\).
- Calculation: \[ \text{Area} = \frac{1}{2} \cdot 7 \cdot 10 \cdot \sin(25^\circ) \] \[ \text{Area} \approx \frac{1}{2} \cdot 7 \cdot 10 \cdot 0.4226 \approx 14.8 \text{ square units} \]
- Example 2:
- Given: \(a = 18\), \(b = 24\), and \(C = 60^\circ\).
- Calculation: \[ \text{Area} = \frac{1}{2} \cdot 18 \cdot 24 \cdot \sin(60^\circ) \] \[ \text{Area} \approx \frac{1}{2} \cdot 18 \cdot 24 \cdot 0.866 \approx 186.2 \text{ square units} \]
This method provides a precise way to calculate the area of triangles when the height is not known or is difficult to measure directly.

Coordinate Geometry Method for Area Calculation
The area of a triangle in coordinate geometry can be determined using the coordinates of its vertices. The formula is derived from the determinant of a matrix formed by these coordinates.
- Given the vertices of a triangle \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\), the area \(A\) can be calculated using the formula:
\[
A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]
This formula calculates the absolute value of the determinant of a 2x2 matrix, ensuring that the area is always positive.
Example Calculation
Let's calculate the area of a triangle with vertices \(A(2, 3)\), \(B(4, 8)\), and \(C(5, 7)\):
- Substitute the coordinates into the formula:
- Simplify the expression:
- Calculate the absolute value and then divide by 2:
\[
A = \frac{1}{2} \left| 2(8 - 7) + 4(7 - 3) + 5(3 - 8) \right|
\]
\[
A = \frac{1}{2} \left| 2(1) + 4(4) + 5(-5) \right| = \frac{1}{2} \left| 2 + 16 - 25 \right| = \frac{1}{2} \left| -7 \right|
\]
\[
A = \frac{1}{2} \times 7 = 3.5
\]
Thus, the area of the triangle is \(3.5\) square units.
Additional Notes
- The formula ensures the area is positive by taking the absolute value.
- This method is useful for triangles whose vertices' coordinates are known, making it a straightforward computational technique.
Examples of Area Calculations
Let's explore some examples to understand how to calculate the area of a triangle using different methods:
Example 1: Using Base and Height
Given a triangle with a base \( b \) of 8 units and a height \( h \) of 5 units, the area can be calculated as:
\[
\text{Area} = \frac{1}{2} \times b \times h = \frac{1}{2} \times 8 \times 5 = 20 \text{ square units}
\]
Example 2: Using Heron's Formula
Consider a triangle with sides \( a = 7 \) units, \( b = 8 \) units, and \( c = 5 \) units. First, calculate the semi-perimeter \( s \):
\[
s = \frac{a + b + c}{2} = \frac{7 + 8 + 5}{2} = 10 \text{ units}
\]
Then, using Heron's formula:
\[
\text{Area} = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{10(10-7)(10-8)(10-5)} = \sqrt{10 \times 3 \times 2 \times 5} = \sqrt{300} \approx 17.32 \text{ square units}
\]
Example 3: Using Trigonometric Method
If we have two sides and the included angle, such as \( a = 6 \) units, \( b = 10 \) units, and \( \angle C = 45^\circ \), the area can be calculated as:
\[
\text{Area} = \frac{1}{2} \times a \times b \times \sin(C) = \frac{1}{2} \times 6 \times 10 \times \sin(45^\circ) = 30 \times \frac{\sqrt{2}}{2} = 15\sqrt{2} \approx 21.21 \text{ square units}
\]
Applications of Triangle Formulas
Triangle formulas have numerous practical applications across various fields. Here are some examples:
-
Engineering:
Engineers frequently use triangle formulas to determine areas and perimeters when designing and analyzing structures, ensuring stability and efficiency. Triangles are fundamental in truss designs, where each triangle's stability helps distribute forces evenly.
-
Architecture:
Architects use these formulas to calculate space requirements, roof pitches, and support structures. Triangular shapes are often employed in modern architecture for aesthetic and structural benefits.
-
Geography:
Geographers use the area and perimeter of triangles in cartography and land surveying. Calculations involving triangles help in accurately mapping out terrain and property boundaries.
-
Navigation:
Triangular calculations are crucial in navigation, particularly in determining positions and plotting courses. The principles of triangulation are used in GPS technology to pinpoint locations.
-
Physics:
In physics, triangle formulas are used to resolve forces, calculate torque, and analyze vectors. Understanding the components of forces and their directions often involves breaking them down into triangular components.
-
Art and Design:
Artists and designers use triangles to create perspective in drawings and to design various objects and patterns. Triangular grids and compositions add balance and symmetry to artwork.
These are just a few examples demonstrating the versatility and importance of triangle formulas in real-world applications.
Real-life Applications
The concepts of perimeter and area of a triangle are not just theoretical but have numerous practical applications in everyday life and various fields. Here are some key real-life applications:
-
Construction of Homes and Buildings:
In architecture and construction, the area and perimeter of triangular sections are crucial for determining the amount of materials needed, such as flooring, roofing, and wall dimensions. Accurate measurements ensure stability and efficient use of resources.
-
Land Measurement:
For agricultural purposes, farmers often need to calculate the perimeter of their fields to build fences or irrigation systems. The area is essential for buying and selling land, ensuring that transactions are fair and based on precise measurements.
-
Road and Bridge Construction:
Engineers use the principles of triangle geometry to design roads and bridges. The area helps in planning the surface required for construction, while the perimeter is used for materials needed for edges and barriers.
-
Art and Design:
Artists and designers use the concepts of area and perimeter in creating various designs, patterns, and layouts. Accurate calculations ensure that their creations are aesthetically pleasing and structurally sound.
-
Computer Graphics:
In computer graphics and gaming, triangles are often used as fundamental building blocks for modeling and rendering complex shapes and scenes. The calculations of area and perimeter help in optimizing the visual details and performance.
-
Astronomy:
Astronomers use triangle geometry to measure distances between celestial objects and their orbits. This helps in understanding the spatial relationships and motions within our universe.
-
Fashion and Textile Design:
Designers calculate the area of fabrics required to create clothing items, while the perimeter is used to determine the amount of trim or border materials needed. Precision in these calculations ensures minimal waste and cost efficiency.
Understanding these applications highlights the importance of mastering the formulas for perimeter and area of triangles. These skills enhance problem-solving abilities and practical knowledge, bridging the gap between theoretical math and real-world applications.

Common Mistakes and Tips
When calculating the perimeter and area of a triangle, students often make several common mistakes. Here are some of the most frequent errors and tips to avoid them:
-
Mistake: Confusing Perimeter and Area
Many students confuse the concepts of perimeter and area. Remember:
- Perimeter: The sum of all sides of a triangle.
- Area: The space enclosed within the triangle, calculated as \( \frac{1}{2} \times \text{base} \times \text{height} \).
-
Mistake: Incorrect Formula Application
Using the wrong formula or forgetting to divide by 2 in the area calculation is a common error. Ensure to use the correct formula for the type of triangle:
- Area: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Perimeter: \( P = a + b + c \)
-
Mistake: Misidentifying Base and Height
For area calculations, it's crucial to correctly identify the base and the perpendicular height. The height must be perpendicular to the base.
-
Mistake: Using Different Units
Ensure all measurements are in the same unit before performing calculations. Convert all measurements to the same unit (e.g., meters to centimeters) before substituting into formulas.
-
Mistake: Neglecting Heron's Formula
For non-right triangles, Heron's Formula is useful for calculating the area when all sides are known:
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)
where \( s \) is the semi-perimeter \( s = \frac{a + b + c}{2} \).
-
Mistake: Incorrectly Using Trigonometric Methods
For triangles where an angle is known, use the trigonometric formula correctly:
\( A = \frac{1}{2} \times a \times b \times \sin(C) \)
Ensure the angle used is between the two known sides.
Tips for Accurate Calculations
- Double-check that the base and height are perpendicular.
- Always use the same unit of measurement throughout the calculation.
- For complex shapes, break them down into simpler triangles and calculate each area separately, then sum them up.
- Review formulas regularly and practice with different types of triangles to build confidence.
Advanced Topics
When studying the perimeter and area of triangles, delving into advanced topics can provide a deeper understanding and appreciation of geometry. Here are some advanced concepts related to triangles:
1. Heron's Formula
Heron's Formula allows for the calculation of the area of a triangle when the lengths of all three sides are known. Given a triangle with sides \(a\), \(b\), and \(c\), and semi-perimeter \(s\) defined as:
\(s = \frac{a + b + c}{2}\)
The area \(A\) can be found using:
\[
A = \sqrt{s(s-a)(s-b)(s-c)}
\]
2. Shoelace Theorem
The Shoelace Theorem provides a way to calculate the area of a triangle when the coordinates of its vertices are known. Given vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area \(A\) is:
\[
A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_1 - x_1y_3 - x_2y_1 - x_3y_2 \right|
\]
3. Trigonometric Methods
For a triangle with sides \(a\), \(b\), and \(c\), and angles \(A\), \(B\), and \(C\), the area can also be calculated using trigonometry:
\[
A = \frac{1}{2} ab \sin(C)
\]
This formula is particularly useful in problems involving oblique triangles where one angle and the two adjacent sides are known.
4. Area Using the Circumradius
The area of a triangle can also be related to its circumradius \(R\), the radius of the circle circumscribing the triangle. Given sides \(a\), \(b\), and \(c\), the area \(A\) is:
\[
A = \frac{abc}{4R}
\]
5. Coordinate Geometry
In coordinate geometry, the area of a triangle can be computed using determinants. For vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area is:
\[
A = \frac{1}{2} \left| \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} \right|
\]
6. Special Triangles and Properties
Exploring special types of triangles, such as isosceles, equilateral, and right triangles, can reveal unique properties and formulas. For example, in an equilateral triangle with side length \(a\), the area is:
\[
A = \frac{\sqrt{3}}{4} a^2
\]
7. Applications in Real Life
Understanding these advanced topics has practical applications in fields such as engineering, architecture, and computer graphics, where precise calculations of areas and perimeters are essential.
These advanced topics provide a comprehensive view of triangle geometry, enhancing both theoretical knowledge and practical problem-solving skills.
Special Triangle Cases
In this section, we explore the perimeter and area calculations for special types of triangles, including equilateral, isosceles, and right-angled triangles.
Equilateral Triangle
An equilateral triangle has all three sides of equal length and each angle measuring 60 degrees.
- Perimeter: For an equilateral triangle with side length \(a\), the perimeter is given by: \[ P = 3a \]
- Area: The area of an equilateral triangle can be calculated using the formula: \[ A = \frac{\sqrt{3}}{4} a^2 \]
Isosceles Triangle
An isosceles triangle has two sides of equal length and two equal angles opposite these sides.
- Perimeter: For an isosceles triangle with equal sides \(l\) and base \(b\), the perimeter is: \[ P = 2l + b \]
- Area: The area can be calculated if the height \(h\) from the base to the opposite vertex is known: \[ A = \frac{1}{2} b h \] Alternatively, using the equal sides \(l\) and base \(b\), the height can be found as: \[ h = \sqrt{l^2 - \left(\frac{b}{2}\right)^2} \] Then, substitute \(h\) back into the area formula.
Right-Angled Triangle
A right-angled triangle has one angle equal to 90 degrees.
- Perimeter: If the lengths of the two legs are \(a\) and \(b\), and the hypotenuse is \(c\) (found using the Pythagorean theorem \(c = \sqrt{a^2 + b^2}\)), the perimeter is: \[ P = a + b + c \]
- Area: The area of a right-angled triangle can be calculated using: \[ A = \frac{1}{2} a b \]
Summary Table of Special Triangles
| Triangle Type | Perimeter Formula | Area Formula |
|---|---|---|
| Equilateral | \(P = 3a\) | \(A = \frac{\sqrt{3}}{4} a^2\) |
| Isosceles | \(P = 2l + b\) | \(A = \frac{1}{2} b \sqrt{l^2 - \left(\frac{b}{2}\right)^2}\) |
| Right-Angled | \(P = a + b + \sqrt{a^2 + b^2}\) | \(A = \frac{1}{2} a b\) |
Additional Resources
Here are some useful resources to deepen your understanding of the perimeter and area of triangles:
-
- Explore detailed explanations of the area and perimeter of triangles.
- Interactive tools to visualize how the area changes with a fixed perimeter.
- Additional topics on various triangle properties and theorems.
-
- Step-by-step tutorials on calculating the area and perimeter of triangles.
- Practice problems with solutions to reinforce learning.
- Additional resources on other geometric shapes and their properties.
-
- Comprehensive guides on the area and perimeter of triangles, including common formulas.
- FAQs to address common questions and challenges.
- Resources for further learning and practice.
These resources provide a mix of theoretical knowledge, practical examples, and interactive tools to help you master the concepts of triangle perimeter and area.
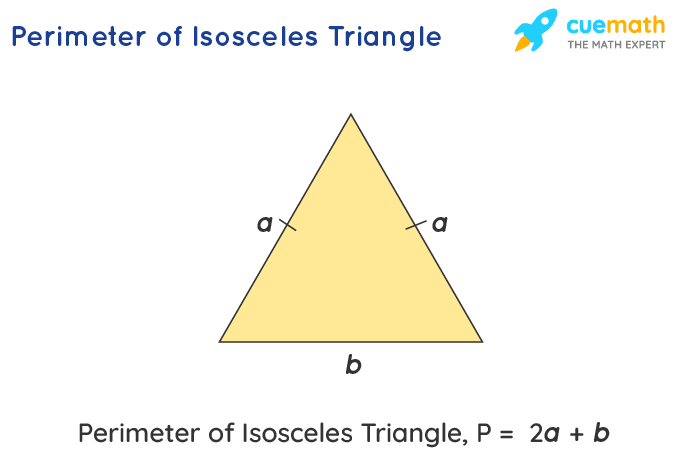
Conclusion
In this comprehensive guide, we have explored various methods to calculate the perimeter and area of a triangle. Understanding these fundamental concepts is crucial in both academic and practical applications. The perimeter of a triangle is the sum of its three sides, which is straightforward to calculate with the formula:
\[ \text{Perimeter} = a + b + c \]
Where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
For calculating the area, we have covered multiple approaches depending on the given information:
- Using Base and Height: The most basic formula is: \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
- Heron's Formula: Useful when all three sides are known: \[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter: \[ s = \frac{a + b + c}{2} \]
- Trigonometric Method: When two sides and the included angle are known: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \]
- Coordinate Geometry: For triangles on a coordinate plane: \[ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
These formulas provide the tools needed to solve various problems involving triangles. Understanding the properties and types of triangles helps in applying the correct formula for accurate results.
The knowledge of perimeter and area is not only essential for solving geometric problems but also has real-life applications in fields such as architecture, engineering, and various branches of science.
In conclusion, mastering the methods to calculate the perimeter and area of triangles enhances our problem-solving skills and mathematical understanding. Keep practicing different problems to gain confidence and proficiency in these fundamental concepts.
Cách Tính Diện Tích và Chu Vi Tam Giác | Toán Học với Thầy J
READ MORE:
Cách Tính Diện Tích và Chu Vi Tam Giác