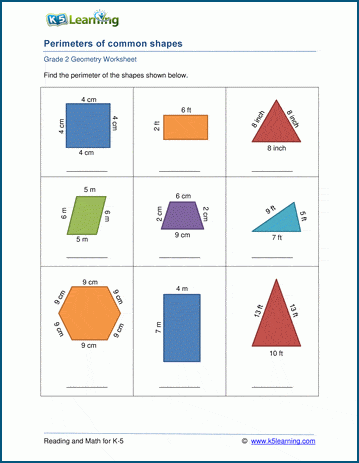
Topic perimeter of a parallelogram formula: Understanding the perimeter of a parallelogram formula is essential for solving geometry problems efficiently. This article provides a comprehensive guide to calculating the perimeter with simple steps and practical examples, making it easy for students and enthusiasts to master this fundamental concept in mathematics. Learn how to apply the formula accurately and avoid common mistakes.
Table of Content
- Formula for the Perimeter of a Parallelogram
- Introduction to Parallelograms
- Basic Properties of Parallelograms
- Understanding the Perimeter
- Formula for the Perimeter of a Parallelogram
- Derivation of the Perimeter Formula
- Steps to Calculate the Perimeter
- Examples of Perimeter Calculations
- Applications of Perimeter in Real Life
- Common Mistakes and How to Avoid Them
- Practice Problems
- FAQs on Perimeter of a Parallelogram
- Conclusion
- YOUTUBE: Video hướng dẫn cách tìm chu vi hình bình hành, giúp bạn dễ dàng hiểu và áp dụng công thức chu vi hình bình hành vào bài toán thực tế.
Formula for the Perimeter of a Parallelogram
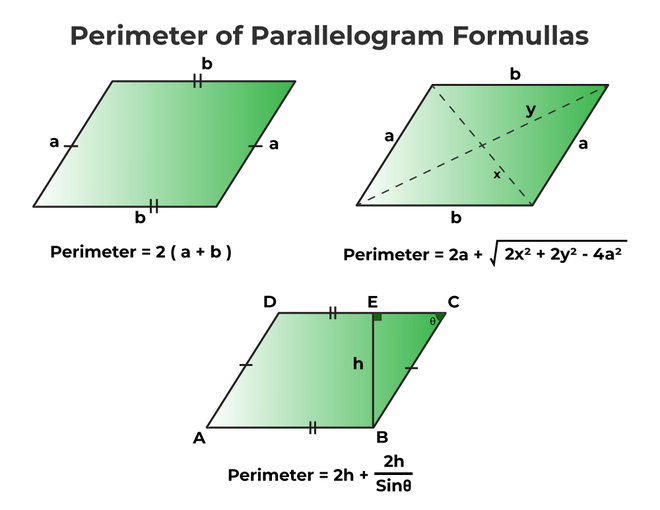
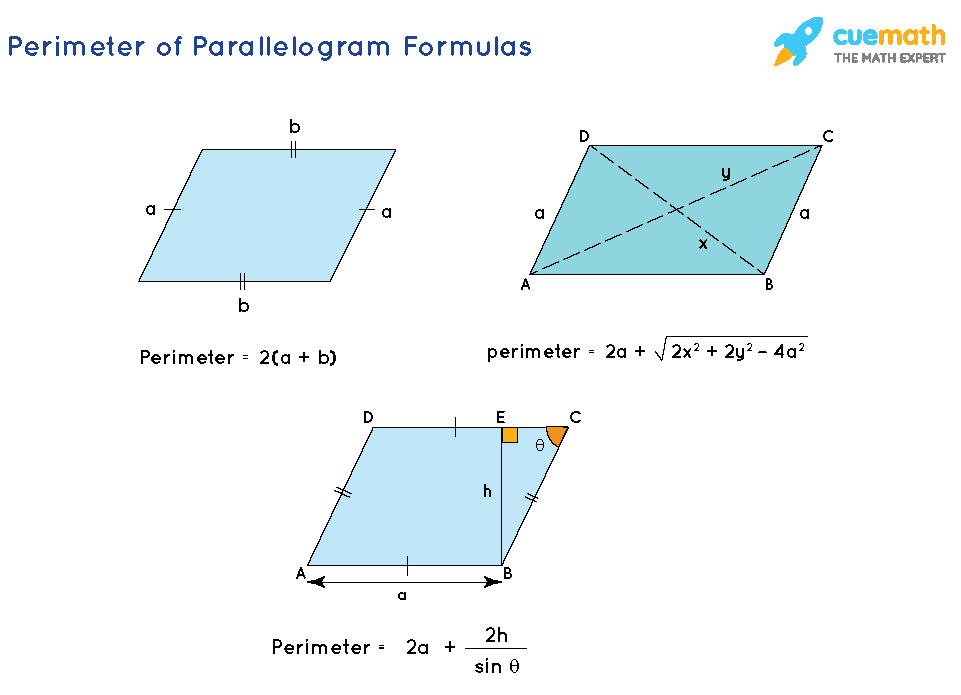
The perimeter of a parallelogram is calculated by adding the lengths of all its sides. A parallelogram has opposite sides that are equal in length. Therefore, the perimeter formula is:
\[ P = 2(a + b) \]
where:
- a is the length of one pair of opposite sides
- b is the length of the other pair of opposite sides
To find the perimeter of a parallelogram, follow these steps:
- Measure the length of one pair of opposite sides and denote it as a.
- Measure the length of the other pair of opposite sides and denote it as b.
- Substitute the values of a and b into the formula \( P = 2(a + b) \).
- Calculate the result to obtain the perimeter.
Example:
- If the lengths of the sides are \( a = 5 \) units and \( b = 7 \) units, the perimeter \( P \) is calculated as follows:
\[ P = 2(5 + 7) = 2 \times 12 = 24 \text{ units} \]
Thus, the perimeter of the parallelogram is 24 units.
READ MORE:
Introduction to Parallelograms
A parallelogram is a four-sided polygon with opposite sides that are equal in length and parallel. The unique properties of parallelograms make them an important shape in geometry. In a parallelogram, opposite angles are equal, and consecutive angles are supplementary, adding up to \(180^\circ\). Understanding these properties is crucial for solving various mathematical problems related to parallelograms.
Key characteristics of parallelograms include:
- Opposite sides are equal and parallel.
- Opposite angles are equal.
- Consecutive angles are supplementary.
- The diagonals bisect each other.
The following are different types of parallelograms:
- Rectangle: A parallelogram with all angles equal to \(90^\circ\).
- Rhombus: A parallelogram with all sides equal in length.
- Square: A parallelogram with all sides equal in length and all angles equal to \(90^\circ\).
These types of parallelograms retain the general properties of parallelograms but also have their own unique characteristics.
In summary, parallelograms are versatile and widely studied shapes in geometry, with specific properties that facilitate the calculation of various parameters, including area and perimeter.
Basic Properties of Parallelograms
Parallelograms are quadrilaterals with specific properties that distinguish them from other geometric shapes. These properties are essential for understanding the behavior of parallelograms and solving related mathematical problems. Here are the basic properties of parallelograms:
- Opposite Sides are Equal and Parallel: In a parallelogram, each pair of opposite sides is equal in length and parallel to each other. If one side is denoted as \( a \) and the adjacent side as \( b \), the opposite sides are also \( a \) and \( b \).
- Opposite Angles are Equal: The angles opposite to each other in a parallelogram are equal. If one angle is \( \theta \), then the angle directly opposite is also \( \theta \).
- Consecutive Angles are Supplementary: The sum of the angles adjacent to each other (consecutive angles) in a parallelogram is \( 180^\circ \). This means if one angle is \( \alpha \), the adjacent angle is \( 180^\circ - \alpha \).
- Diagonals Bisect Each Other: The diagonals of a parallelogram intersect at their midpoints, effectively bisecting each other. If the diagonals are denoted as \( d_1 \) and \( d_2 \), each diagonal is divided into two equal parts at the point of intersection.
These properties can be summarized in the following table:
| Property | Description |
| Opposite Sides | Equal and Parallel |
| Opposite Angles | Equal |
| Consecutive Angles | Supplementary (sum to \(180^\circ\)) |
| Diagonals | Bisect Each Other |
Understanding these properties allows for deeper insights into the geometry of parallelograms and provides a foundation for more advanced geometric concepts and calculations.
Understanding the Perimeter
The perimeter of a parallelogram is the total distance around the outside of the shape. To understand the perimeter, it's essential to know the basic structure of a parallelogram and its properties.
A parallelogram is a quadrilateral with opposite sides that are equal and parallel. The perimeter is calculated by adding the lengths of all the sides. However, since opposite sides are equal, the perimeter can be simplified to twice the sum of the lengths of two adjacent sides.
The formula for the perimeter of a parallelogram is given by:
\[ P = 2(a + b) \]
Where:
- a is the length of one pair of opposite sides.
- b is the length of the other pair of opposite sides.
Let's break down the understanding of the perimeter step by step:
- Identify the lengths of two adjacent sides, a and b.
- Sum these two lengths: \( a + b \).
- Multiply the sum by 2 to account for both pairs of equal sides: \( 2(a + b) \).
This formula works for any parallelogram, regardless of the lengths of its sides, as long as you correctly identify the lengths of two adjacent sides.
For example, if a parallelogram has sides of length 5 cm and 7 cm, the perimeter would be:
\[ P = 2(5 + 7) = 2 \times 12 = 24 \, \text{cm} \]
Understanding this concept is crucial for solving problems related to the perimeter of parallelograms, as it forms the basis for more complex geometrical calculations and real-life applications.
Formula for the Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around the outside of the shape. This is calculated by adding the lengths of all four sides. Given that the opposite sides of a parallelogram are equal, we can simplify the formula for its perimeter.
Let's denote the lengths of the two pairs of opposite sides as \( a \) and \( b \). The perimeter \( P \) can be calculated using the formula:
\[ P = 2a + 2b \]
or
\[ P = 2(a + b) \]
Here is a step-by-step method to calculate the perimeter:
- Identify the lengths of the adjacent sides of the parallelogram. Let these lengths be \( a \) and \( b \).
- Sum the lengths of these sides: \( a + b \).
- Multiply the result by 2 to account for both pairs of opposite sides: \( 2(a + b) \).
For example, if a parallelogram has sides of lengths 8 cm and 5 cm, the perimeter would be calculated as follows:
- Sum the side lengths: \( 8 + 5 = 13 \) cm
- Multiply by 2: \( 2 \times 13 = 26 \) cm
Thus, the perimeter is 26 cm.
In some cases, you might have different information, such as the lengths of the diagonals and one side. In such scenarios, the perimeter can be found using the properties of the diagonals and the law of cosines:
\[ b = \sqrt{\frac{(x^2 + y^2 - 2a^2)}{2}} \]
\[ P = 2a + 2b \]
Where \( x \) and \( y \) are the lengths of the diagonals and \( a \) is the length of the known side.
For instance, if a parallelogram has one side of length 7 cm and diagonals of 9 cm and 11 cm, the unknown side \( b \) can be calculated as:
\[ b = \sqrt{\frac{(9^2 + 11^2 - 2 \cdot 7^2)}{2}} \approx 8.06 \, \text{cm} \]
Then, the perimeter is:
\[ P = 2(7 + 8.06) \approx 30.12 \, \text{cm} \]
Derivation of the Perimeter Formula
The perimeter of a parallelogram is derived based on its geometric properties. Here, we will explain the derivation step-by-step:
-
Understanding the Basic Structure: A parallelogram has two pairs of opposite sides that are equal in length. Let's denote the lengths of the adjacent sides as \(a\) and \(b\).
-
Basic Perimeter Formula: The perimeter (\(P\)) of a parallelogram is the total distance around the figure, which includes two lengths of \(a\) and two lengths of \(b\). Thus, the formula is:
\[
P = a + b + a + b = 2a + 2b = 2(a + b)
\] -
Using Diagonals: When the lengths of the diagonals (\(d_1\) and \(d_2\)) are given along with one side (\(a\)), the perimeter can also be expressed using the diagonals. The formula becomes more complex:
\[
P = 2a + \sqrt{2d_1^2 + 2d_2^2 - 4a^2}
\] -
With Base, Height, and Angle: If the base (\(b\)), height (\(h\)), and an interior angle (\(\theta\)) are known, the perimeter can be derived using trigonometric relationships:
\[
P = 2a + 2\frac{h}{\sin \theta}
\]
Let's consider an example to illustrate the derivation:
-
Example: Given a parallelogram with sides \(a = 5 \, \text{cm}\) and \(b = 8 \, \text{cm}\), calculate the perimeter.
\[
P = 2(a + b) = 2(5 \, \text{cm} + 8 \, \text{cm}) = 2(13 \, \text{cm}) = 26 \, \text{cm}
\]
This straightforward example shows how the basic formula for the perimeter of a parallelogram is applied. Understanding these derivations helps in comprehending the geometric properties and relationships within a parallelogram.
Steps to Calculate the Perimeter
Calculating the perimeter of a parallelogram involves adding the lengths of all four sides. Since opposite sides of a parallelogram are equal, the formula simplifies to adding the lengths of the two adjacent sides and then doubling the result.
-
Identify the Lengths of Adjacent Sides:
Determine the lengths of the two adjacent sides of the parallelogram. Let these sides be \( a \) and \( b \).
-
Apply the Perimeter Formula:
Use the formula for the perimeter \( P \) of a parallelogram:
\[
P = 2(a + b)
\] -
Perform the Calculation:
Substitute the lengths of the sides into the formula and calculate the perimeter. For example, if \( a = 5 \) units and \( b = 7 \) units:
\[
P = 2(5 + 7) = 2 \times 12 = 24 \text{ units}
\] -
Verify Your Results:
Check your calculations to ensure accuracy. If the problem involves measurements with units, be sure to include the correct units in your final answer.
Here are a couple of examples to illustrate these steps:
-
Example 1: Find the perimeter of a parallelogram with sides \( a = 8 \) cm and \( b = 5 \) cm.
\[
P = 2(8 + 5) = 2 \times 13 = 26 \text{ cm}
\] -
Example 2: Calculate the perimeter of a parallelogram where one side is 10 m and the adjacent side is 6 m.
\[
P = 2(10 + 6) = 2 \times 16 = 32 \text{ m}
\]
By following these steps, you can easily calculate the perimeter of any parallelogram, ensuring you have accurate and reliable results.
Examples of Perimeter Calculations
Understanding how to calculate the perimeter of a parallelogram can be clarified through practical examples. Here, we provide a few examples to illustrate the process step by step.
Example 1: Simple Calculation
Consider a parallelogram with sides of lengths 5 cm and 8 cm. To find the perimeter:
- Identify the lengths of the adjacent sides: \(a = 5 \, \text{cm}\) and \(b = 8 \, \text{cm}\).
- Use the perimeter formula: \( P = 2(a + b) \).
- Substitute the values into the formula: \( P = 2(5 \, \text{cm} + 8 \, \text{cm}) \).
- Calculate the sum inside the parentheses: \( 5 \, \text{cm} + 8 \, \text{cm} = 13 \, \text{cm} \).
- Multiply by 2: \( P = 2 \times 13 \, \text{cm} = 26 \, \text{cm} \).
Therefore, the perimeter of the parallelogram is 26 cm.
Example 2: Using Given Perimeter to Find Missing Side
Given a parallelogram with a base of 5 cm and a perimeter of 40 cm, determine the length of the other side.
- Let \(a = 5 \, \text{cm}\) and the perimeter \( P = 40 \, \text{cm} \).
- Use the perimeter formula: \( P = 2(a + b) \).
- Substitute the known values: \( 40 \, \text{cm} = 2(5 \, \text{cm} + b) \).
- Simplify the equation: \( 40 \, \text{cm} = 10 \, \text{cm} + 2b \).
- Isolate \( b \): \( 40 \, \text{cm} - 10 \, \text{cm} = 2b \).
- Solve for \( b \): \( 30 \, \text{cm} = 2b \) and \( b = \frac{30 \, \text{cm}}{2} = 15 \, \text{cm} \).
The length of the other side is 15 cm.
Example 3: Different Side Lengths
Consider a parallelogram with sides of 9 cm and 7 cm. To find the perimeter:
- Identify the lengths of the adjacent sides: \(a = 9 \, \text{cm}\) and \(b = 7 \, \text{cm}\).
- Use the perimeter formula: \( P = 2(a + b) \).
- Substitute the values into the formula: \( P = 2(9 \, \text{cm} + 7 \, \text{cm}) \).
- Calculate the sum inside the parentheses: \( 9 \, \text{cm} + 7 \, \text{cm} = 16 \, \text{cm} \).
- Multiply by 2: \( P = 2 \times 16 \, \text{cm} = 32 \, \text{cm} \).
Thus, the perimeter of the parallelogram is 32 cm.
Applications of Perimeter in Real Life
The concept of perimeter is not just confined to mathematics; it has numerous practical applications in our daily lives. Understanding how to calculate and use perimeter can help in various fields and everyday tasks. Here are some key real-life applications:
-
Construction and Architecture:
In building homes and structures, knowing the perimeter helps in determining the boundaries and overall layout. It ensures that the design is precise and that materials are used efficiently. For example, when planning the layout of a house, the perimeter measurements are crucial for determining the length of walls and the amount of materials needed.
-
Fencing and Landscaping:
For setting up fences or boundaries around a property, calculating the perimeter allows for an accurate estimation of the amount of fencing material required. This application is also important in landscaping projects where defining areas for gardens or lawns involves perimeter calculations.
-
Sports Fields:
The dimensions of various sports fields and tracks are determined using perimeter calculations. For instance, setting up a soccer field or a running track requires precise measurements to ensure fairness and consistency in the sport.
-
Urban Planning:
Urban planners use perimeter calculations to design efficient road networks, parks, and other public spaces. The perimeter helps in defining the layout and ensuring that spaces are used optimally.
-
Art and Fashion:
In the world of art and fashion, perimeter is used to create designs and patterns. Whether it’s tailoring a dress or designing an accessory, understanding the perimeter helps in cutting fabric or other materials accurately.
-
Computer Graphics:
In computer graphics, accurate visual representations of objects often require precise perimeter calculations. This is crucial in various industries, including gaming and animation, where realistic graphics are essential.
Understanding the perimeter is not only helpful in academic settings but also essential for practical applications in real life, enabling us to make informed decisions and effectively utilize resources.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a parallelogram can be straightforward, but there are some common mistakes students often make. Here are those mistakes and tips on how to avoid them:
- Incorrectly Identifying Adjacent Sides:
Ensure you correctly identify the adjacent sides of the parallelogram. Remember, the formula for the perimeter is \(P = 2(a + b)\), where \(a\) and \(b\) are the lengths of two adjacent sides. Confusing adjacent sides with opposite sides can lead to incorrect calculations.
- Mixing Up Units:
Always use the same units for both side lengths. If the lengths are given in different units (e.g., one in centimeters and the other in meters), convert them to the same unit before applying the formula.
- Incorrect Addition:
Double-check your addition of the side lengths. Simple arithmetic mistakes can lead to wrong results. Make sure \(a + b\) is calculated accurately before multiplying by 2.
- Misinterpreting Given Data:
Sometimes, problems provide additional information such as angles or diagonals. Stick to the given lengths of the adjacent sides for the perimeter calculation, unless specifically instructed otherwise.
- Formula Misapplication:
Ensure you're using the correct formula for the shape. The perimeter of a parallelogram is \(P = 2(a + b)\). Using formulas from other shapes like rectangles or trapezoids will result in incorrect answers.
By being mindful of these common mistakes and following these tips, you can accurately calculate the perimeter of a parallelogram every time.
Practice Problems
Here are some practice problems to help you understand and apply the formula for the perimeter of a parallelogram:
-
Find the perimeter of a parallelogram with a base of 10 cm and a side length of 7 cm.
Solution:
\[
P = 2(a + b) = 2(10 \, \text{cm} + 7 \, \text{cm}) = 2 \times 17 \, \text{cm} = 34 \, \text{cm}
\] -
A parallelogram has a base of 8 m and a side length of 5 m. Calculate its perimeter.
Solution:
\[
P = 2(a + b) = 2(8 \, \text{m} + 5 \, \text{m}) = 2 \times 13 \, \text{m} = 26 \, \text{m}
\] -
The perimeter of a parallelogram is 60 inches. If one side is 18 inches, what is the length of the other side?
Solution:
\[
P = 2(a + b) = 60 \, \text{inches}
\]
\[
a + b = 30 \, \text{inches}
\]
\[
b = 30 \, \text{inches} - 18 \, \text{inches} = 12 \, \text{inches}
\] -
Calculate the perimeter of a parallelogram with sides of 15 cm and 20 cm.
Solution:
\[
P = 2(a + b) = 2(15 \, \text{cm} + 20 \, \text{cm}) = 2 \times 35 \, \text{cm} = 70 \, \text{cm}
\] -
A parallelogram has a perimeter of 84 meters. One side is 24 meters long. Determine the length of the other side.
Solution:
\[
P = 2(a + b) = 84 \, \text{meters}
\]
\[
a + b = 42 \, \text{meters}
\]
\[
b = 42 \, \text{meters} - 24 \, \text{meters} = 18 \, \text{meters}
\]
FAQs on Perimeter of a Parallelogram
Below are some frequently asked questions (FAQs) about the perimeter of a parallelogram, along with detailed answers to help clarify common doubts.
-
Q1: What is the perimeter of a parallelogram?
A: The perimeter is calculated by adding the lengths of all four sides. If the lengths of the adjacent sides are \( a \) and \( b \), the perimeter \( P \) is given by the formula:
\[
P = 2(a + b)
\] -
Q2: Why is knowing the perimeter important?
A: Knowing the perimeter is important for various practical applications such as surveying land, estimating the amount of material needed for fencing, and architectural design. It also helps in calculating other geometrical properties.
-
Q3: How do you derive the perimeter formula?
A: The perimeter of a parallelogram is derived by adding the lengths of all four sides. Since opposite sides of a parallelogram are equal, the formula simplifies to twice the sum of the lengths of any two adjacent sides:
\[
P = 2(a + b)
\] -
Q4: Can you provide an example calculation?
A: Sure! For a parallelogram with sides \( a = 5 \) cm and \( b = 7 \) cm:
\[
P = 2(a + b) = 2(5 + 7) = 2 \times 12 = 24 \text{ cm}
\] -
Q5: What are common mistakes to avoid when calculating the perimeter?
A: Common mistakes include forgetting to multiply the sum of the adjacent sides by 2 and confusing the perimeter with the area. Always ensure you add the correct lengths and double the sum for accuracy.
-
Q6: What are real-life applications of calculating the perimeter of a parallelogram?
A: Real-life applications include land measurement, construction projects, and any scenario requiring boundary measurements. For example, determining the amount of fencing needed for a garden with a parallelogram shape.
Conclusion
Understanding the perimeter of a parallelogram is essential for solving various mathematical problems and real-life applications. By mastering the perimeter formula, you can easily determine the distance around any parallelogram when given the lengths of its sides.
To summarize:
- The perimeter of a parallelogram is calculated using the formula:
P = 2(a + b) - In this formula, a and b represent the lengths of the adjacent sides of the parallelogram.
Key points to remember:
- Ensure you have accurate measurements of both side lengths.
- Double-check your calculations to avoid common mistakes.
- Apply the formula consistently to various problems to reinforce your understanding.
By applying these steps, you can confidently calculate the perimeter of any parallelogram, making use of this knowledge in both academic and real-world scenarios. Practice regularly with different examples and problems to solidify your comprehension and skills.
We hope this guide has provided a clear and comprehensive understanding of how to calculate the perimeter of a parallelogram. With consistent practice, you will be able to tackle related problems with ease and accuracy.

Video hướng dẫn cách tìm chu vi hình bình hành, giúp bạn dễ dàng hiểu và áp dụng công thức chu vi hình bình hành vào bài toán thực tế.
Cách Tìm Chu Vi Hình Bình Hành
READ MORE:
Video hướng dẫn chi tiết cách tính chu vi hình bình hành, giúp bạn nắm vững công thức và áp dụng vào các bài toán thực tế.
Cách Tính Chu Vi Hình Bình Hành