Topic area and perimeter of a triangle: Unlock the secrets of calculating the area and perimeter of a triangle with our comprehensive guide. Whether you're a student, teacher, or math enthusiast, this article provides clear formulas, practical examples, and step-by-step instructions to master these essential geometric concepts. Dive in and enhance your understanding of triangles today!
Table of Content
- Area and Perimeter of a Triangle
- Introduction
- Basic Concepts of Triangles
- Formulas for Area of a Triangle
- Calculating Area Using Base and Height
- Heron's Formula for Area
- Area Calculation Using Coordinates
- Special Cases of Triangles
- Equilateral Triangle Area
- Right Triangle Area
- Isosceles Triangle Area
- Formulas for Perimeter of a Triangle
- Calculating Perimeter Using Side Lengths
- Perimeter Calculation Using Coordinates
- Special Cases for Perimeter
- Equilateral Triangle Perimeter
- Right Triangle Perimeter
- Isosceles Triangle Perimeter
- Applications of Triangle Area and Perimeter
- YOUTUBE: Video hướng dẫn cách tìm diện tích và chu vi tam giác với thầy J. Học cách tính diện tích và chu vi tam giác một cách dễ hiểu và chi tiết.
Area and Perimeter of a Triangle
Area of a Triangle
The area of a triangle can be calculated using various methods depending on the information available.
1. Using Base and Height
When the base \(b\) and height \(h\) of the triangle are known, the area \(A\) is given by:
\[
A = \frac{1}{2} \times b \times h
\]
2. Using Heron's Formula
When the lengths of all three sides of the triangle are known, the area can be calculated using Heron's formula. Let the sides be \(a\), \(b\), and \(c\). First, calculate the semi-perimeter \(s\):
\[
s = \frac{a + b + c}{2}
\]
Then, the area \(A\) is:
\[
A = \sqrt{s(s-a)(s-b)(s-c)}
\]
3. Using Coordinates (Shoelace Formula)
If the coordinates of the vertices of the triangle are known, the area can be calculated using the Shoelace formula. For a triangle with vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area \(A\) is:
\[
A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]
Perimeter of a Triangle
The perimeter \(P\) of a triangle is the sum of the lengths of its sides.
1. Using Side Lengths
If the lengths of all three sides \(a\), \(b\), and \(c\) are known, the perimeter \(P\) is given by:
\[
P = a + b + c
\]
2. Using Coordinates
If the coordinates of the vertices of the triangle are known, the lengths of the sides can be calculated using the distance formula. For vertices \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the side lengths are:
- \[ a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- \[ b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- \[ c = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
Then, the perimeter \(P\) is:
\[
P = a + b + c
\]

READ MORE:
Introduction
Understanding the area and perimeter of a triangle is fundamental in geometry. These calculations are not only essential for academic purposes but also have practical applications in various fields such as architecture, engineering, and art. This guide will provide you with the formulas, methods, and examples to master these concepts.
A triangle is a three-sided polygon, and calculating its area and perimeter depends on the type of triangle and the information available. Below, we will explore different methods to find these measurements.
- Area: The region enclosed by the triangle. It can be calculated using different formulas based on the given data, such as the base and height, side lengths, or coordinates of the vertices.
- Perimeter: The total length of the triangle's sides. It is simply the sum of the lengths of all three sides.
Let's delve into the various methods for calculating the area and perimeter of a triangle, step by step, ensuring a thorough understanding of each approach.
Basic Concepts of Triangles
Triangles are fundamental shapes in geometry, defined by three sides and three angles. Understanding the basic properties and types of triangles is crucial for calculating their area and perimeter.
- Sides: A triangle has three sides, usually denoted as \(a\), \(b\), and \(c\).
- Angles: The three interior angles of a triangle add up to \(180^\circ\).
Types of Triangles
Triangles can be classified based on their sides and angles:
- By Sides:
- Equilateral Triangle: All three sides are equal, and all three angles are \(60^\circ\).
- Isosceles Triangle: Two sides are equal, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and angles are different.
- By Angles:
- Acute Triangle: All three angles are less than \(90^\circ\).
- Right Triangle: One angle is exactly \(90^\circ\).
- Obtuse Triangle: One angle is greater than \(90^\circ\).
Properties of Triangles
Triangles have several important properties:
- Sum of Interior Angles: The sum of the three interior angles is always \(180^\circ\).
- Exterior Angles: The exterior angle is equal to the sum of the two opposite interior angles.
- Triangle Inequality Theorem: The sum of the lengths of any two sides must be greater than the length of the remaining side.
These basic concepts are foundational for understanding how to calculate the area and perimeter of triangles, which we will explore in the subsequent sections.
Formulas for Area of a Triangle
The area of a triangle can be calculated using several different formulas, depending on the information available. Here, we will discuss the most common methods:
- Using Base and Height: The most straightforward formula to calculate the area of a triangle is by using its base and height.
The formula is given by:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\] - Heron's Formula: This formula is useful when you know the lengths of all three sides of the triangle. Let the sides be \(a\), \(b\), and \(c\).
- First, calculate the semi-perimeter (\(s\)):
\[
s = \frac{a + b + c}{2}
\] - Then, apply Heron's formula:
\[
\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}
\]
- First, calculate the semi-perimeter (\(s\)):
- Using Coordinates: When the vertices of the triangle are given in a coordinate plane, the area can be calculated using the coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\).
The formula is given by:
\[
\text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
\]
These formulas allow you to determine the area of a triangle based on different sets of given information, making them versatile tools in geometry.
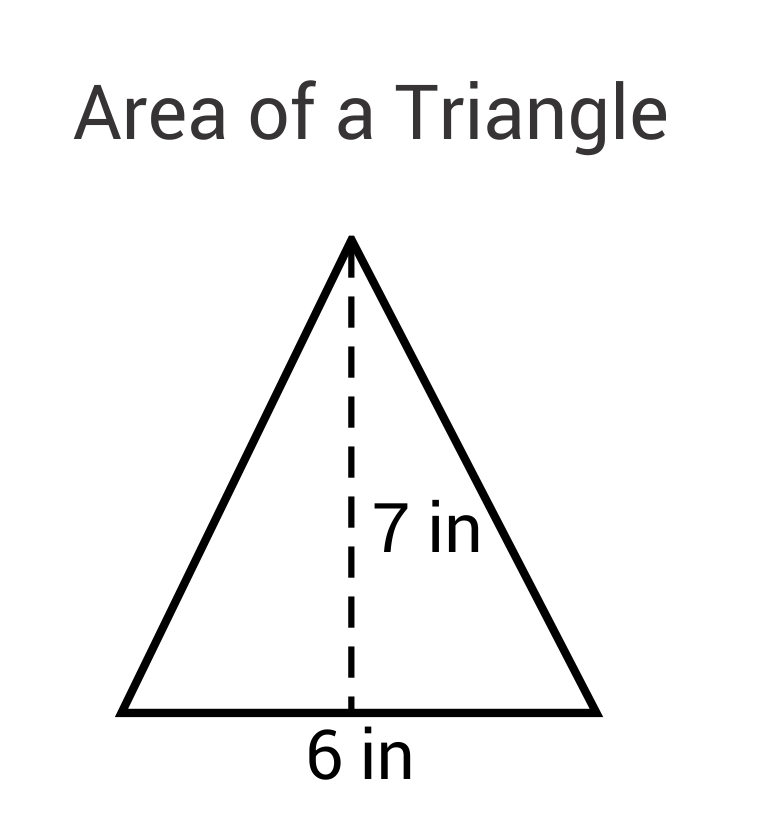
Calculating Area Using Base and Height
The area of a triangle can be calculated using the base and height with a simple and straightforward formula. This method is especially useful for triangles where the base and height are easily identifiable.
The formula for the area of a triangle is given by:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Here's a step-by-step guide to calculate the area of a triangle using its base and height:
- Identify the base and height: The base of the triangle can be any one of its sides, but it is typically chosen as the one which is most convenient for measurement. The height is the perpendicular distance from the base to the opposite vertex.
- Measure the base: Use a ruler or measuring tape to find the length of the base. Record this measurement in the appropriate units (e.g., centimeters, meters).
- Measure the height: The height is the perpendicular distance from the chosen base to the opposite vertex. Ensure that this measurement is taken at a right angle to the base. Record this measurement as well.
- Apply the formula: Substitute the measured base and height into the formula. Multiply the base by the height, and then divide the result by 2.
For example, if the base of a triangle is 8 cm and the height is 5 cm, the area is calculated as follows:
\[ \text{Area} = \frac{1}{2} \times 8 \, \text{cm} \times 5 \, \text{cm} = 20 \, \text{cm}^2 \]
Therefore, the area of the triangle is 20 square centimeters.
This method of calculation is applicable to all types of triangles, including equilateral, isosceles, and scalene triangles, as long as the base and height can be determined.
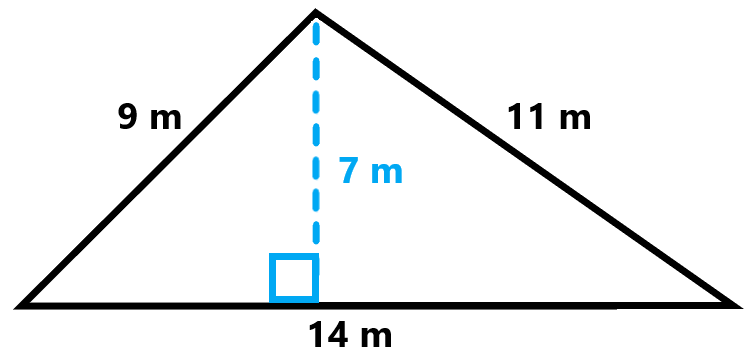
Heron's Formula for Area
Heron's formula is a useful method for finding the area of a triangle when the lengths of all three sides are known. The formula involves two main steps: calculating the semi-perimeter of the triangle and then using it to find the area.
-
Calculate the Semi-Perimeter (s)
The semi-perimeter of a triangle is half of its perimeter. Given a triangle with side lengths \(a\), \(b\), and \(c\), the semi-perimeter is calculated as follows:
\[
s = \frac{a + b + c}{2}
\] -
Apply Heron's Formula
Once the semi-perimeter is known, the area \(A\) of the triangle can be found using Heron's formula:
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
Let's go through an example to see how Heron's formula is applied:
-
Example:
Consider a triangle with side lengths \(a = 5\), \(b = 6\), and \(c = 7\).
-
First, calculate the semi-perimeter:
\[
s = \frac{5 + 6 + 7}{2} = 9
\] -
Next, apply Heron's formula:
\[
A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = \sqrt{9 \cdot 4 \cdot 3 \cdot 2} = \sqrt{216} \approx 14.7
\]So, the area of the triangle is approximately 14.7 square units.
-
Heron's formula is particularly useful because it does not require knowledge of the height of the triangle, making it versatile for various applications.
Area Calculation Using Coordinates
When the vertices of a triangle are given in a coordinate plane, the area can be calculated using the coordinates of these vertices. Suppose the vertices of the triangle are \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\). The formula for calculating the area is:
\[ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
Follow these steps to calculate the area:
Identify the coordinates of the vertices of the triangle. Let's denote them as:
- Vertex A: \((x_1, y_1)\)
- Vertex B: \((x_2, y_2)\)
- Vertex C: \((x_3, y_3)\)
Substitute the coordinates into the formula:
\[ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]Calculate the values within the parentheses:
- Calculate \(y_2 - y_3\)
- Calculate \(y_3 - y_1\)
- Calculate \(y_1 - y_2\)
Multiply each result by the corresponding \(x\)-coordinate:
- Multiply \(x_1\) by \(y_2 - y_3\)
- Multiply \(x_2\) by \(y_3 - y_1\)
- Multiply \(x_3\) by \(y_1 - y_2\)
Add these three products together:
\[ x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \]Take the absolute value of the sum:
\[ \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]Divide by 2 to get the area of the triangle:
\[ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
Let's look at an example:
Suppose the vertices of a triangle are \((2, 3)\), \((4, 8)\), and \((5, 2)\). To find the area:
- Identify the coordinates: \((x_1, y_1) = (2, 3)\), \((x_2, y_2) = (4, 8)\), \((x_3, y_3) = (5, 2)\).
- Substitute into the formula:
- Calculate each term:
- Add the results:
- Take the absolute value:
- Divide by 2:
\[ \text{Area} = \frac{1}{2} \left| 2(8 - 2) + 4(2 - 3) + 5(3 - 8) \right| \]
\[ 2(6) + 4(-1) + 5(-5) = 12 - 4 - 25 \]
\[ 12 - 4 - 25 = -17 \]
\[ \left| -17 \right| = 17 \]
\[ \text{Area} = \frac{17}{2} = 8.5 \]
Therefore, the area of the triangle with vertices at \((2, 3)\), \((4, 8)\), and \((5, 2)\) is \(8.5\) square units.
Special Cases of Triangles
Triangles come in various types, each with unique properties that simplify the calculation of area and perimeter. Here, we will explore the special cases of equilateral, isosceles, and right triangles.
Equilateral Triangle
An equilateral triangle has all three sides of equal length and all three angles equal to 60 degrees. This symmetry simplifies both area and perimeter calculations.
- Perimeter: Since all sides are equal, the perimeter \( P \) is simply: \[ P = 3a \] where \( a \) is the length of a side.
- Area: The area \( A \) can be calculated using the formula: \[ A = \frac{\sqrt{3}}{4} a^2 \] This formula derives from splitting the equilateral triangle into two 30-60-90 right triangles.
Isosceles Triangle
An isosceles triangle has two sides of equal length. The properties of isosceles triangles make certain calculations more straightforward.
- Perimeter: If the equal sides are \( a \) and the base is \( b \), the perimeter \( P \) is: \[ P = 2a + b \]
- Area: The area \( A \) can be found using the height \( h \) from the base to the apex: \[ A = \frac{b \cdot h}{2} \] The height can be calculated using the Pythagorean theorem in the right triangle formed by the height, half the base, and the equal side: \[ h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \]
Right Triangle
A right triangle has one angle of 90 degrees. The side opposite this angle is the hypotenuse, and the other two sides are the legs.
- Perimeter: The perimeter \( P \) is the sum of all three sides: \[ P = a + b + c \] where \( c \) is the hypotenuse, and \( a \) and \( b \) are the legs.
- Area: The area \( A \) is calculated as: \[ A = \frac{1}{2} a b \] This formula comes from the fact that the legs of the triangle form the base and height of a right triangle.
Scalene Triangle
A scalene triangle has all sides and angles of different lengths and degrees. While it doesn't have the symmetries of the other triangles, its area and perimeter can be calculated using general formulas.
- Perimeter: The perimeter \( P \) is: \[ P = a + b + c \] where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Area: The area \( A \) can be calculated using Heron's formula: \[ A = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter: \[ s = \frac{a + b + c}{2} \]
Understanding these special cases helps in quickly calculating the properties of triangles in various geometric problems.
Equilateral Triangle Area
An equilateral triangle is a special type of triangle where all three sides are equal in length, and all three internal angles are each 60 degrees. The area of an equilateral triangle can be calculated using a specific formula derived from its unique properties.
Formula for Area
The formula for the area of an equilateral triangle is:
\[
A = \frac{\sqrt{3}}{4} a^2
\]
where \(a\) is the length of each side of the triangle.
Derivation of the Formula
The formula is derived by considering the height of the equilateral triangle. If we draw a perpendicular from one vertex to the opposite side, it bisects the triangle into two 30-60-90 right triangles. The height (h) can be calculated using the Pythagorean theorem:
\[
h = \frac{\sqrt{3}}{2} a
\]
Using the basic area formula for a triangle (Area = 1/2 × base × height), we substitute the base as \(a\) and the height as \(\frac{\sqrt{3}}{2} a\):
\[
A = \frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2
\]
Examples
Let's look at a few examples to better understand how to use this formula:
- Example 1: Calculate the area of an equilateral triangle with a side length of 6 cm.
- Given: \(a = 6\) cm
- Using the formula: \(A = \frac{\sqrt{3}}{4} a^2\)
- \[ A = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \text{ cm}^2 \]
- Example 2: Find the area of an equilateral triangle with a perimeter of 24 cm.
- Given: Perimeter = 24 cm
- Each side \(a = \frac{24}{3} = 8\) cm
- Using the formula: \(A = \frac{\sqrt{3}}{4} a^2\)
- \[ A = \frac{\sqrt{3}}{4} \times 8^2 = \frac{\sqrt{3}}{4} \times 64 = 16\sqrt{3} \text{ cm}^2 \]
Properties of Equilateral Triangles
Some important properties of equilateral triangles include:
- All sides are equal.
- All angles are 60 degrees.
- They are also known as regular triangles.
- The height (h) can be calculated as \(\frac{\sqrt{3}}{2} a\).
- The perimeter (P) is \(3a\).

Right Triangle Area
A right triangle is a triangle where one of the angles is exactly 90 degrees. The area of a right triangle can be calculated easily using the base and height, which are the two sides that form the right angle.
To find the area of a right triangle, you can use the following formula:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Here, the base and height are the lengths of the two legs of the triangle that are perpendicular to each other.
Let's go through the steps to calculate the area of a right triangle:
- Identify the base and height: In a right triangle, the base and height are the two sides that form the right angle.
- Measure the base and height: Ensure you have the lengths of the base and height. For example, let the base (b) be 3 units and the height (h) be 4 units.
- Apply the formula: Substitute the values of the base and height into the formula.
\[ \text{Area} = \frac{1}{2} \times 3 \times 4 = \frac{1}{2} \times 12 = 6 \text{ square units} \]
This calculation shows that the area of the right triangle with a base of 3 units and a height of 4 units is 6 square units.
Additionally, if you only know the hypotenuse and one leg, you can find the other leg using the Pythagorean theorem:
\[ \text{hypotenuse}^2 = \text{base}^2 + \text{height}^2 \]
For example, if the hypotenuse is 5 units and the base is 3 units:
\[ 5^2 = 3^2 + \text{height}^2 \]
\[ 25 = 9 + \text{height}^2 \]
\[ \text{height}^2 = 16 \]
\[ \text{height} = \sqrt{16} = 4 \text{ units} \]
Once you have both the base and the height, you can apply the area formula.
By following these steps, you can easily calculate the area of any right triangle using its base and height.
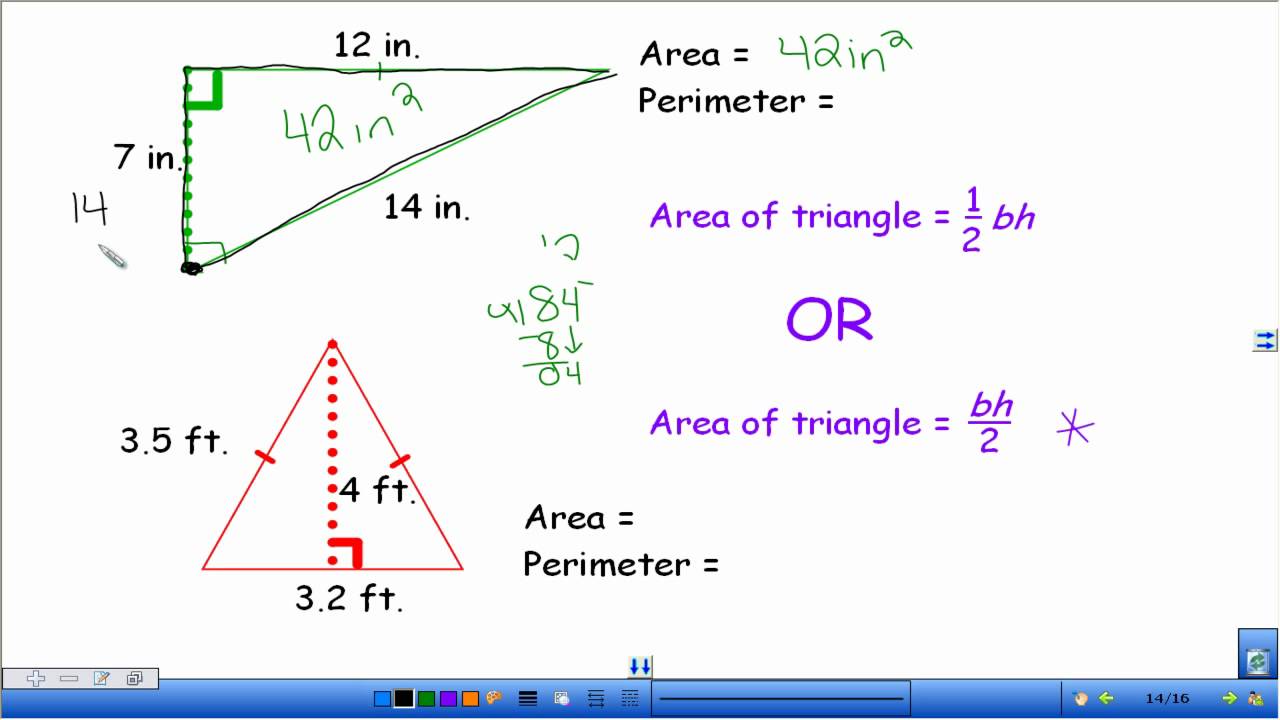
Isosceles Triangle Area
An isosceles triangle is a triangle with two sides of equal length. To calculate the area of an isosceles triangle, we can use the base and height or apply trigonometric properties. Here, we'll discuss both methods:
Method 1: Using Base and Height
The area \(A\) of an isosceles triangle can be calculated using the formula:
\[ A = \frac{1}{2} \times \text{base} \times \text{height} \]
- Identify the base (\(b\)) of the triangle. This is the unequal side.
- Measure or determine the height (\(h\)), which is the perpendicular distance from the base to the apex (the point where the equal sides meet).
- Apply the formula to calculate the area.
For example, if the base is 6 units and the height is 4 units:
\[ A = \frac{1}{2} \times 6 \times 4 = 12 \text{ square units} \]
Method 2: Using Side Lengths and Trigonometry
If the height is not known, we can use the Pythagorean theorem to find it, provided we know the lengths of the equal sides and the base:
Given an isosceles triangle with equal sides of length \(a\) and base \(b\), the height \(h\) can be found using the formula:
\[ h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \]
- Measure the lengths of the equal sides (\(a\)) and the base (\(b\)).
- Calculate half of the base, \(\frac{b}{2}\).
- Apply the formula to find the height (\(h\)).
- Use the height to calculate the area using the base-height formula.
For example, if the equal sides are 5 units each and the base is 6 units:
\[ h = \sqrt{5^2 - \left(\frac{6}{2}\right)^2} = \sqrt{25 - 9} = \sqrt{16} = 4 \text{ units} \]
Then the area is:
\[ A = \frac{1}{2} \times 6 \times 4 = 12 \text{ square units} \]
Example Calculation
Consider an isosceles triangle with equal sides of 10 units and a base of 12 units:
- Calculate the height:
\[ h = \sqrt{10^2 - \left(\frac{12}{2}\right)^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \text{ units} \] - Calculate the area:
\[ A = \frac{1}{2} \times 12 \times 8 = 48 \text{ square units} \]
Formulas for Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle, which can be calculated by summing the lengths of its sides. Depending on the information available, different formulas can be used to determine the perimeter.
1. Using Side Lengths (SSS - Side-Side-Side)
If all three sides of the triangle are known, the perimeter (P) can be calculated using the simple formula:
\[ P = a + b + c \]
Where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
- Example: For a triangle with sides \( a = 4 \, \text{cm} \), \( b = 5 \, \text{cm} \), and \( c = 6 \, \text{cm} \):
\( P = 4 \, \text{cm} + 5 \, \text{cm} + 6 \, \text{cm} = 15 \, \text{cm} \)
2. Using Two Sides and the Included Angle (SAS - Side-Angle-Side)
If two sides and the included angle are known, the perimeter can be calculated by first finding the third side using the law of cosines and then summing all sides:
\[ c = \sqrt{a^2 + b^2 - 2ab \cos(\gamma)} \]
\[ P = a + b + c \]
Where \( a \) and \( b \) are the known sides, and \( \gamma \) is the included angle.
- Example: For a triangle with sides \( a = 5 \, \text{cm} \), \( b = 7 \, \text{cm} \), and included angle \( \gamma = 60^\circ \):
\( c = \sqrt{5^2 + 7^2 - 2 \cdot 5 \cdot 7 \cdot \cos(60^\circ)} = \sqrt{25 + 49 - 70 \cdot 0.5} = \sqrt{34} \approx 5.83 \, \text{cm} \)
\( P = 5 \, \text{cm} + 7 \, \text{cm} + 5.83 \, \text{cm} = 17.83 \, \text{cm} \)
3. Using Two Angles and One Side (ASA - Angle-Side-Angle)
If two angles and one side between them are known, the perimeter can be calculated using the law of sines to find the other two sides and then summing all sides:
\[ b = a \frac{\sin(\beta)}{\sin(\alpha + \beta)} \]
\[ c = a \frac{\sin(\gamma)}{\sin(\alpha + \gamma)} \]
\[ P = a + b + c \]
Where \( a \) is the known side, and \( \beta \) and \( \gamma \) are the known angles.
- Example: For a triangle with side \( a = 6 \, \text{cm} \), and angles \( \beta = 45^\circ \) and \( \gamma = 60^\circ \):
\( b = 6 \, \text{cm} \cdot \frac{\sin(45^\circ)}{\sin(105^\circ)} \approx 6 \, \text{cm} \cdot 0.707 / 0.9659 \approx 4.39 \, \text{cm} \)
\( c = 6 \, \text{cm} \cdot \frac{\sin(60^\circ)}{\sin(105^\circ)} \approx 6 \, \text{cm} \cdot 0.866 / 0.9659 \approx 5.38 \, \text{cm} \)
\( P = 6 \, \text{cm} + 4.39 \, \text{cm} + 5.38 \, \text{cm} = 15.77 \, \text{cm} \)
4. Perimeter in Special Cases
Special triangles like equilateral, isosceles, and right triangles have simplified perimeter calculations:
- Equilateral Triangle:
All sides are equal, so if side length \( a \) is known:
\[ P = 3a \]
- Isosceles Triangle:
Two sides are equal, so if the equal sides are \( a \) and the base is \( b \):
\[ P = 2a + b \]
- Right Triangle:
With legs \( a \) and \( b \), and hypotenuse \( c \):
\[ c = \sqrt{a^2 + b^2} \]
\[ P = a + b + c \]
Calculating Perimeter Using Side Lengths
The perimeter of a triangle is the total distance around the triangle, which is found by summing the lengths of its sides. Here are detailed steps and formulas to calculate the perimeter based on different given data.
Formula for Perimeter with Known Side Lengths
If you know the lengths of all three sides of the triangle, you can use the simple formula:
\( P = a + b + c \)
Where \( P \) is the perimeter, and \( a \), \( b \), and \( c \) are the lengths of the sides.
Example
Suppose you have a triangle with sides of lengths 5 cm, 7 cm, and 9 cm. The perimeter is calculated as:
\( P = 5 \, \text{cm} + 7 \, \text{cm} + 9 \, \text{cm} = 21 \, \text{cm} \)
Perimeter with Two Sides and the Included Angle (SAS)
When you know two sides and the included angle, use the Law of Cosines to find the third side, then sum all sides:
\( P = a + b + \sqrt{a^2 + b^2 - 2ab \cos(\gamma)} \)
Where \( \gamma \) is the included angle between sides \( a \) and \( b \).
Example
Given sides \( a = 8 \, \text{cm} \), \( b = 6 \, \text{cm} \), and the angle \( \gamma = 60^\circ \), the perimeter is calculated as:
\( c = \sqrt{8^2 + 6^2 - 2 \cdot 8 \cdot 6 \cdot \cos(60^\circ)} \)
\( c = \sqrt{64 + 36 - 96 \cdot 0.5} = \sqrt{64 + 36 - 48} = \sqrt{52} \approx 7.21 \, \text{cm} \)
Thus, the perimeter \( P \) is:
\( P = 8 \, \text{cm} + 6 \, \text{cm} + 7.21 \, \text{cm} = 21.21 \, \text{cm} \)
Perimeter with Two Angles and a Side (ASA)
When two angles and the included side are known, use the Law of Sines to find the other two sides and then the perimeter:
\( P = a + \left( \frac{a \sin(\beta)}{\sin(\alpha)} \right) + \left( \frac{a \sin(\gamma)}{\sin(\alpha)} \right) \)
Where \( a \) is the known side, and \( \alpha \) and \( \beta \) are the known angles opposite the unknown sides.
Example
Given side \( a = 5 \, \text{cm} \), and angles \( \beta = 45^\circ \) and \( \gamma = 60^\circ \), the perimeter is:
\( P = 5 \, \text{cm} + \left( \frac{5 \sin(45^\circ)}{\sin(75^\circ)} \right) + \left( \frac{5 \sin(60^\circ)}{\sin(75^\circ)} \right) \)
\( P = 5 \, \text{cm} + 3.66 \, \text{cm} + 4.33 \, \text{cm} = 13 \, \text{cm} \)
These formulas allow you to calculate the perimeter of any triangle as long as you have the necessary side lengths or angles.
Perimeter Calculation Using Coordinates
To calculate the perimeter of a triangle when the coordinates of its vertices are known, follow these steps:
-
Identify the coordinates of the vertices. Let the vertices be A(\(x_1, y_1\)), B(\(x_2, y_2\)), and C(\(x_3, y_3\)).
-
Calculate the lengths of the sides using the distance formula:
- Length of side AB:
\[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] - Length of side BC:
\[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \] - Length of side CA:
\[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- Length of side AB:
-
Add the lengths of the sides to get the perimeter:
- \[ \text{Perimeter} = AB + BC + CA \]
Let's consider an example. Suppose we have a triangle with vertices A(1, 2), B(4, 5), and C(4, 0). To find the perimeter:
-
Calculate the lengths of the sides:
- \[ AB = \sqrt{(4 - 1)^2 + (5 - 2)^2} = \sqrt{3^2 + 3^2} = \sqrt{18} = 3\sqrt{2} \]
- \[ BC = \sqrt{(4 - 4)^2 + (0 - 5)^2} = \sqrt{0 + (-5)^2} = \sqrt{25} = 5 \]
- \[ CA = \sqrt{(4 - 1)^2 + (0 - 2)^2} = \sqrt{3^2 + (-2)^2} = \sqrt{13} \]
-
Add the lengths of the sides to find the perimeter:
- \[ \text{Perimeter} = 3\sqrt{2} + 5 + \sqrt{13} \approx 3 \cdot 1.414 + 5 + 3.606 = 4.242 + 5 + 3.606 = 12.848 \]
Thus, the perimeter of the triangle is approximately 12.85 units.
Special Cases for Perimeter
Calculating the perimeter of certain types of triangles can be simplified due to their unique properties. Below, we discuss the special cases for equilateral, isosceles, and right triangles.
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula to calculate the perimeter (P) is straightforward:
\[ P = 3a \]
where \( a \) is the length of one side.
Example: If each side of an equilateral triangle is 5 cm, then the perimeter is:
\[ P = 3 \times 5 = 15 \text{ cm} \]
Isosceles Triangle
An isosceles triangle has two sides of equal length. To find its perimeter, use the following formula:
\[ P = 2a + b \]
where \( a \) is the length of the two equal sides and \( b \) is the length of the base.
Example: If the equal sides are 7 cm each and the base is 10 cm, then the perimeter is:
\[ P = 2 \times 7 + 10 = 24 \text{ cm} \]
Right Triangle
A right triangle has one right angle (90 degrees). The perimeter can be found if the lengths of the two legs (a and b) are known, and the hypotenuse (c) can be calculated using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Once you have the hypotenuse, the perimeter is:
\[ P = a + b + c \]
Example: For a right triangle with legs of 3 cm and 4 cm, the hypotenuse is:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ cm} \]
Then, the perimeter is:
\[ P = 3 + 4 + 5 = 12 \text{ cm} \]
Understanding these formulas allows for quick and accurate calculation of the perimeter, making it easier to solve problems related to equilateral, isosceles, and right triangles.
Equilateral Triangle Perimeter
The perimeter of an equilateral triangle is straightforward to calculate. An equilateral triangle has three sides of equal length. If each side of the equilateral triangle is denoted as \( a \), the formula for the perimeter \( P \) is:
Perimeter Formula:
\[ P = 3a \]
Here is a step-by-step guide to calculate the perimeter of an equilateral triangle:
- Measure the length of one side of the equilateral triangle. Let's denote this length as \( a \).
- Multiply the length of one side by 3, since all three sides are equal.
- The resulting value is the perimeter of the triangle.
Let's look at an example to illustrate this:
- Example: If each side of an equilateral triangle is 5 cm, the perimeter is calculated as follows:
- Using the formula \( P = 3a \), substitute \( a = 5 \):
- \[ P = 3 \times 5 = 15 \, \text{cm} \]
Therefore, the perimeter of the equilateral triangle with each side measuring 5 cm is 15 cm.
Right Triangle Perimeter
The perimeter of a right triangle can be calculated easily once the lengths of its three sides are known. A right triangle has one 90-degree angle, and its sides include the two legs (a and b) and the hypotenuse (c), which is the longest side opposite the right angle.
To calculate the perimeter, you can use the following steps:
-
Identify the lengths of the two legs (a and b) and the hypotenuse (c). If only the legs are known, the hypotenuse can be found using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
-
Add the lengths of the three sides to find the perimeter:
\[
\text{Perimeter} = a + b + c
\]
Here is an example to illustrate the calculation:
- Given a right triangle with legs \(a = 3\) units and \(b = 4\) units, first calculate the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]
- Then, find the perimeter by summing all three sides: \[ \text{Perimeter} = 3 + 4 + 5 = 12 \text{ units} \]
If only the hypotenuse and one leg are known, you can still find the other leg using the Pythagorean theorem rearranged:
\[
a = \sqrt{c^2 - b^2}
\]
Once all sides are known, you simply add them together to get the perimeter. This method ensures that the calculation is accurate and straightforward.
In summary, the key steps to determine the perimeter of a right triangle are:
- Use the Pythagorean theorem if necessary to find the missing side.
- Add the lengths of all three sides to find the perimeter.
Isosceles Triangle Perimeter
The perimeter of an isosceles triangle is calculated by adding the lengths of its three sides. In an isosceles triangle, two sides are of equal length, and the third side is the base.
To find the perimeter, use the following formula:
\[ P = 2a + b \]
where \( a \) is the length of the two equal sides, and \( b \) is the length of the base.
Here is a step-by-step process to calculate the perimeter of an isosceles triangle:
- Measure the length of one of the equal sides (let's call this \( a \)).
- Measure the length of the base (let's call this \( b \)).
- Double the length of the equal side to account for both equal sides.
- Add the doubled length to the length of the base to find the perimeter.
For example, if an isosceles triangle has equal sides of length 5 cm and a base of 8 cm, the perimeter is calculated as follows:
\[ P = 2 \cdot 5 + 8 = 10 + 8 = 18 \, \text{cm} \]
Therefore, the perimeter of the triangle is 18 cm.
Using this simple formula, you can easily find the perimeter of any isosceles triangle by knowing the lengths of its sides.
Applications of Triangle Area and Perimeter
Understanding the area and perimeter of triangles has numerous practical applications in various fields. Below are some detailed examples illustrating these applications:
1. Construction and Architecture
Triangles, particularly right and equilateral triangles, are fundamental in construction and architecture due to their structural stability.
- Design and Structural Analysis: Architects use triangles to design trusses, roofs, and bridges because they distribute weight evenly and maintain rigidity.
- Land Measurement: Surveyors often use triangular plots to divide land, ensuring accurate area calculation for property boundaries.
2. Engineering
Engineers apply the principles of triangle area and perimeter in various projects to ensure precision and safety.
- Mechanical Engineering: Triangular supports and braces are used in machinery to provide strength without adding excessive weight.
- Civil Engineering: Triangular elements are essential in the design of infrastructures such as bridges, towers, and dams to enhance stability.
3. Navigation and Mapping
In navigation and cartography, triangles help in accurate location plotting and map creation.
- Triangulation: This technique involves forming triangles to determine distances and map out regions accurately.
- GPS Technology: The Global Positioning System uses triangular calculations to pinpoint exact locations on the Earth’s surface.
4. Art and Design
Artists and designers incorporate triangles to create visually appealing and balanced compositions.
- Graphic Design: Triangular shapes are used to guide the viewer's eye and create dynamic layouts.
- Interior Design: Triangular patterns and elements can add aesthetic value and structural interest to spaces.
5. Real-Life Examples
Triangles are present in various everyday objects and scenarios.
- Fencing: Calculating the perimeter of triangular plots helps determine the amount of material needed for fencing.
- Gardening: Triangular garden beds maximize space and create interesting layouts in landscaping.
6. Education and Problem Solving
Teaching the concepts of area and perimeter of triangles helps students develop critical thinking and problem-solving skills.
- Mathematics Education: Students learn to apply geometric principles to solve complex problems involving triangles.
- STEM Projects: Engaging in projects that require triangle measurements fosters a deeper understanding of scientific and mathematical concepts.
These applications underscore the importance of mastering the concepts of triangle area and perimeter, as they play a crucial role in various practical and theoretical contexts.
Video hướng dẫn cách tìm diện tích và chu vi tam giác với thầy J. Học cách tính diện tích và chu vi tam giác một cách dễ hiểu và chi tiết.
Cách Tìm Diện Tích và Chu Vi Tam Giác | Toán Học với Thầy J
READ MORE:
Video hướng dẫn cách tìm diện tích và chu vi tam giác. Học cách tính diện tích và chu vi tam giác một cách dễ hiểu và chi tiết.
Cách Tìm Diện Tích và Chu Vi Tam Giác











