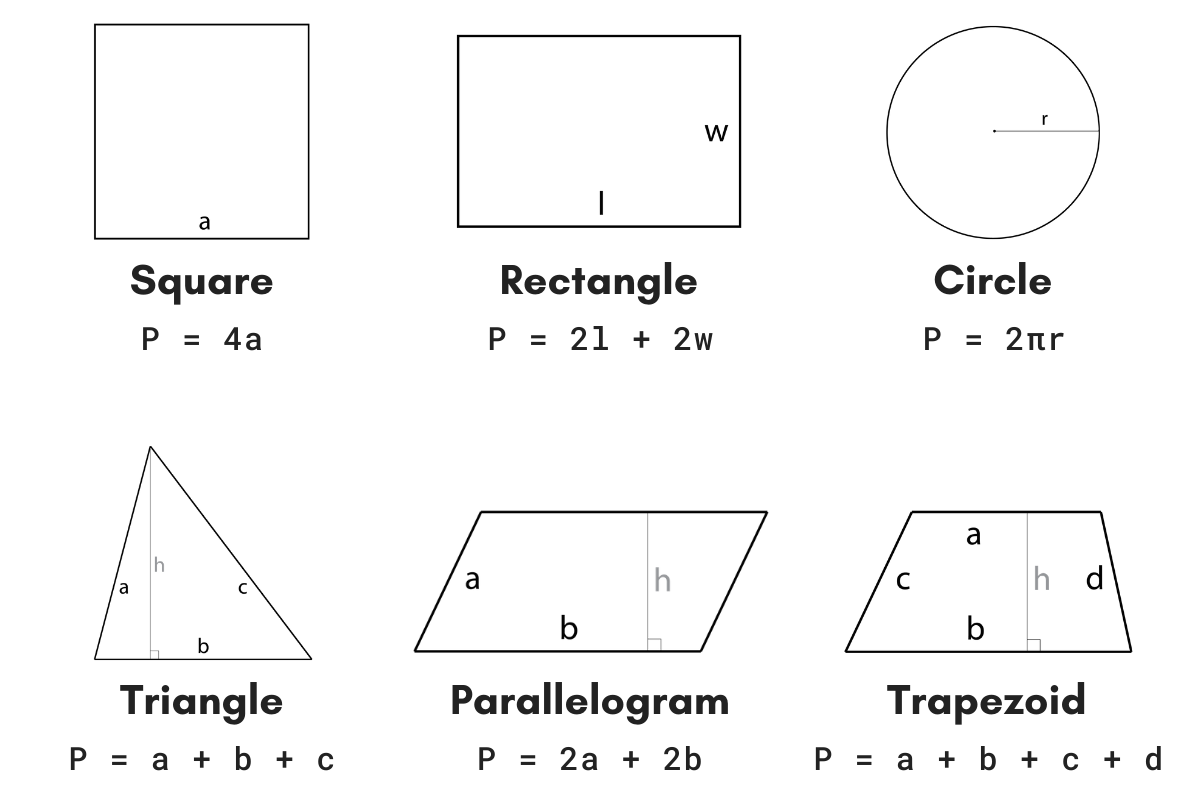
Topic area and perimeter of a triangle formula: Understanding the area and perimeter of a triangle is essential for students and professionals alike. This comprehensive guide will delve into the various formulas used to calculate these measurements, providing step-by-step examples and practical applications to enhance your knowledge and skills. Let's explore the fascinating world of triangle geometry together.
Table of Content
- Area and Perimeter of a Triangle
- Introduction to Triangles
- Basic Concepts of Triangles
- Types of Triangles
- Understanding Area and Perimeter
- Formulas for Area of a Triangle
- Base and Height Method
- Heron's Formula
- Trigonometric Method
- Formulas for Perimeter of a Triangle
- Perimeter Using Side Lengths
- Special Cases for Perimeter
- Step-by-Step Calculation Examples
- Example Using Base and Height
- Example Using Heron's Formula
- Example Using Trigonometry
- Applications of Area and Perimeter in Real Life
- Common Mistakes and Tips
- FAQs about Triangle Calculations
- YOUTUBE: Hướng dẫn chi tiết cách tính diện tích và chu vi của tam giác. Video này sẽ giúp bạn hiểu rõ các công thức và phương pháp tính toán.
Area and Perimeter of a Triangle
Area of a Triangle
The area of a triangle can be calculated using different formulas depending on the given information. Here are the most common formulas:
- Using Base and Height: The formula for the area \(A\) of a triangle with base \(b\) and height \(h\) is:
$$A = \frac{1}{2} \times b \times h$$
- Using Heron's Formula: For a triangle with sides of lengths \(a\), \(b\), and \(c\), and semi-perimeter \(s\) where \(s = \frac{a + b + c}{2}\), the area \(A\) is:
$$A = \sqrt{s(s-a)(s-b)(s-c)}$$
- Using Trigonometry: For a triangle with sides \(a\) and \(b\) and included angle \(C\), the area \(A\) is:
$$A = \frac{1}{2} \times a \times b \times \sin(C)$$
Perimeter of a Triangle
The perimeter \(P\) of a triangle is the sum of the lengths of its sides. For a triangle with sides \(a\), \(b\), and \(c\), the formula is:
$$P = a + b + c$$
Example Calculations
- Example 1: Given a triangle with base \(b = 5\) units and height \(h = 3\) units, the area \(A\) is:
$$A = \frac{1}{2} \times 5 \times 3 = 7.5 \text{ square units}$$
- Example 2: For a triangle with sides \(a = 3\) units, \(b = 4\) units, and \(c = 5\) units:
Semi-perimeter \(s = \frac{3 + 4 + 5}{2} = 6\)
Area \(A = \sqrt{6(6-3)(6-4)(6-5)} = \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{36} = 6 \text{ square units}$$
Perimeter \(P = 3 + 4 + 5 = 12 \text{ units}$$

READ MORE:
Introduction to Triangles
Triangles are one of the fundamental shapes in geometry, defined by three sides and three angles. They come in various types and have unique properties that make them essential in both theoretical and applied mathematics. Understanding triangles is crucial for mastering more complex geometric concepts and solving practical problems in fields like engineering, architecture, and astronomy.
Key characteristics of triangles include:
- Three Sides: The three sides of a triangle can be of varying lengths, leading to different classifications such as equilateral, isosceles, and scalene.
- Three Angles: The sum of the internal angles of a triangle is always 180 degrees. These angles determine the triangle's type: acute, right, or obtuse.
- Vertices: The points where the sides of a triangle meet are called vertices.
Triangles are classified based on their sides and angles:
- Equilateral Triangle: All three sides and angles are equal, with each angle measuring 60 degrees.
- Isosceles Triangle: Has two sides of equal length and two equal angles opposite these sides.
- Scalene Triangle: All three sides and angles are of different lengths and measures.
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One of the angles is exactly 90 degrees.
- Obtuse Triangle: One of the angles is greater than 90 degrees.
Understanding the area and perimeter of triangles involves knowing the appropriate formulas. For instance, the area can be calculated using:
- Base and Height Method: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Heron's Formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s \) is the semi-perimeter \( s = \frac{a+b+c}{2} \)
- Trigonometric Method: \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \)
By mastering these formulas and understanding the properties of triangles, you can solve a wide range of geometric problems effectively.
Basic Concepts of Triangles
Triangles are the simplest polygon, characterized by three edges and three vertices. To fully understand triangles, one must grasp several basic concepts, including types of triangles, properties, and fundamental formulas.
Types of Triangles: Triangles can be classified based on side lengths and angles:
- Equilateral Triangle: All three sides and angles are equal, with each angle measuring 60 degrees.
- Isosceles Triangle: Has two sides of equal length and two equal angles opposite these sides.
- Scalene Triangle: All three sides and angles are of different lengths and measures.
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One of the angles is exactly 90 degrees.
- Obtuse Triangle: One of the angles is greater than 90 degrees.
Properties of Triangles:
- Sum of Angles: The sum of the interior angles of a triangle is always 180 degrees.
- Pythagorean Theorem: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides: \(a^2 + b^2 = c^2\).
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.
Formulas for Area: The area of a triangle can be found using various methods:
- Base and Height Method: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Heron's Formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s \) is the semi-perimeter \( s = \frac{a+b+c}{2} \)
- Trigonometric Method: \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \)
Formulas for Perimeter: The perimeter of a triangle is the sum of its side lengths:
- Standard Formula: \( \text{Perimeter} = a + b + c \)
By mastering these basic concepts, one can effectively analyze and solve various problems involving triangles.
Types of Triangles
Triangles are categorized based on their sides and angles. Each type has distinct properties and formulas for calculating area and perimeter. Understanding these classifications is crucial for solving geometric problems effectively.
Classification by Sides:
- Equilateral Triangle: All three sides and angles are equal. Each angle measures 60 degrees.
- Area Formula: \( \text{Area} = \frac{\sqrt{3}}{4} \times a^2 \)
- Perimeter Formula: \( \text{Perimeter} = 3a \)
- Isosceles Triangle: Has two sides of equal length and two equal angles opposite these sides.
- Area Formula: \( \text{Area} = \frac{1}{2} \times b \times h \) where \( b \) is the base and \( h \) is the height.
- Perimeter Formula: \( \text{Perimeter} = 2a + b \) where \( a \) is the length of the equal sides.
- Scalene Triangle: All three sides and angles are of different lengths and measures.
- Area Formula: Use Heron's Formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s \) is the semi-perimeter \( s = \frac{a+b+c}{2} \).
- Perimeter Formula: \( \text{Perimeter} = a + b + c \).
Classification by Angles:
- Acute Triangle: All three angles are less than 90 degrees.
- Any of the area and perimeter formulas for equilateral, isosceles, or scalene triangles can be applied depending on the side lengths.
- Right Triangle: One of the angles is exactly 90 degrees.
- Area Formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \) where the base and height are the two sides that form the right angle.
- Perimeter Formula: \( \text{Perimeter} = a + b + c \) where \( c \) is the hypotenuse.
- Pythagorean Theorem: In a right triangle, \( a^2 + b^2 = c^2 \).
- Obtuse Triangle: One of the angles is greater than 90 degrees.
- Any of the area and perimeter formulas for equilateral, isosceles, or scalene triangles can be applied depending on the side lengths.
Understanding Area and Perimeter
Calculating the area and perimeter of a triangle is fundamental in geometry. These measurements help in determining the space within a triangle and the total length of its boundaries. Below, we will explore the concepts and formulas for calculating both area and perimeter.
Area of a Triangle: The area of a triangle represents the space enclosed within its three sides. There are multiple methods to calculate this area:
- Base and Height Method:
- Formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- This method requires knowing the base and the height (the perpendicular distance from the base to the opposite vertex).
- Heron's Formula:
- Formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \)
- Here, \( s \) is the semi-perimeter: \( s = \frac{a+b+c}{2} \), and \( a, b, c \) are the side lengths.
- This formula is useful when all three side lengths are known.
- Trigonometric Method:
- Formula: \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \)
- This method requires two sides and the included angle.
Perimeter of a Triangle: The perimeter of a triangle is the total length of its sides. The formula varies depending on the known dimensions:
- Standard Perimeter Formula:
- Formula: \( \text{Perimeter} = a + b + c \)
- Used when all side lengths are known.
- Special Cases:
- For an equilateral triangle: \( \text{Perimeter} = 3a \) where \( a \) is the length of a side.
- For an isosceles triangle: \( \text{Perimeter} = 2a + b \) where \( a \) are the equal sides and \( b \) is the base.
By mastering these formulas and methods, one can efficiently calculate the area and perimeter of any triangle, facilitating the solving of complex geometric problems and practical applications in various fields.

Formulas for Area of a Triangle
Calculating the area of a triangle can be done using several methods, each suited to different known values. Below are the primary formulas used to find the area of a triangle:
1. Base and Height Method:
This is the most straightforward method, requiring the base and the corresponding height (the perpendicular distance from the base to the opposite vertex).
- Formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Steps:
- Identify the base of the triangle.
- Measure the height, which is the perpendicular distance from the base to the opposite vertex.
- Apply the formula to calculate the area.
2. Heron's Formula:
Heron's formula is useful when all three side lengths are known. It involves calculating the semi-perimeter first.
- Formula: \[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \] where \( s \) is the semi-perimeter: \[ s = \frac{a+b+c}{2} \]
- Steps:
- Measure the lengths of all three sides \(a\), \(b\), and \(c\).
- Calculate the semi-perimeter \(s\).
- Apply the formula to find the area.
3. Trigonometric Method:
This method is applied when two sides and the included angle are known.
- Formula: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \] where \(a\) and \(b\) are the sides, and \(C\) is the included angle.
- Steps:
- Identify the lengths of the two sides \(a\) and \(b\).
- Measure the included angle \(C\).
- Use the formula to calculate the area.
4. Special Case - Equilateral Triangle:
For an equilateral triangle, where all sides are equal, a specific formula can be used.
- Formula: \[ \text{Area} = \frac{\sqrt{3}}{4} \times a^2 \] where \(a\) is the length of a side.
- Steps:
- Measure the length of a side.
- Apply the formula to find the area.
These formulas allow for flexible and accurate calculation of the area of various types of triangles, making it easier to solve geometric problems and apply this knowledge in practical scenarios.
Base and Height Method
The Base and Height Method is one of the simplest ways to calculate the area of a triangle. This method requires the length of the base and the perpendicular height from the base to the opposite vertex.
Formula:
The formula for calculating the area using the base and height is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Steps to Calculate the Area:
- Identify the Base: Choose one side of the triangle to be the base. Any side can be chosen, but typically the longest side or the most convenient one for measurement is used.
- Measure the Height: Measure the perpendicular distance from the chosen base to the opposite vertex. This is the height of the triangle.
- Apply the Formula: Plug the base and height values into the formula:
- If the base is \(b\) and the height is \(h\), then: \[ \text{Area} = \frac{1}{2} \times b \times h \]
- Calculate the Area: Perform the multiplication and division to find the area of the triangle.
Example Calculation:
Suppose you have a triangle with a base of 8 cm and a height of 5 cm. The area calculation would be as follows:
- Base (\(b\)) = 8 cm
- Height (\(h\)) = 5 cm
- Applying the formula: \[ \text{Area} = \frac{1}{2} \times 8 \times 5 = 20 \, \text{cm}^2 \]
This method is particularly useful for right triangles, where the legs can serve as the base and height. However, it is also applicable to any triangle by properly identifying and measuring the base and height.
Heron's Formula
Heron's Formula is a powerful method for calculating the area of a triangle when the lengths of all three sides are known. It is especially useful for scalene triangles, where no sides are equal, and no height is readily available.
Formula:
The formula for Heron's Formula is:
\[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
where \( s \) is the semi-perimeter of the triangle:
\[ s = \frac{a+b+c}{2} \]
and \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
Steps to Calculate the Area:
- Measure the Side Lengths: Obtain the lengths of all three sides of the triangle: \( a \), \( b \), and \( c \).
- Calculate the Semi-Perimeter: Use the formula for the semi-perimeter:
- \( s = \frac{a+b+c}{2} \)
- Apply Heron's Formula: Substitute the values of \( a \), \( b \), \( c \), and \( s \) into Heron's Formula:
- \[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
- Calculate the Area: Perform the arithmetic operations inside the square root first, then take the square root to find the area.
Example Calculation:
Suppose you have a triangle with side lengths of 7 cm, 8 cm, and 9 cm. The area calculation would be as follows:
- Side lengths: \( a = 7 \, \text{cm} \), \( b = 8 \, \text{cm} \), \( c = 9 \, \text{cm} \)
- Calculate the semi-perimeter: \[ s = \frac{7 + 8 + 9}{2} = 12 \, \text{cm} \]
- Apply Heron's Formula: \[ \text{Area} = \sqrt{12(12-7)(12-8)(12-9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.83 \, \text{cm}^2 \]
Heron's Formula is a versatile tool for finding the area of any triangle when side lengths are known, providing accurate results without the need for height measurements.
Trigonometric Method
The trigonometric method for finding the area of a triangle involves using the sine of one of its angles. This method is particularly useful when you know two sides of a triangle and the included angle between them. The formula is:
\( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \)
Where:
- \(a\) and \(b\) are the lengths of two sides of the triangle.
- \(C\) is the included angle between sides \(a\) and \(b\).
Here's a step-by-step guide to using the trigonometric method:
- Identify the lengths of the two sides and the included angle.
- Ensure the angle is in degrees or convert it to radians if necessary.
- Use the formula \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \).
- Calculate the sine of the included angle.
- Multiply the lengths of the two sides and the sine of the angle.
- Divide the product by 2 to get the area of the triangle.
For example, if you have a triangle with sides \(a = 7\) cm, \(b = 9\) cm, and the included angle \(C = 30^\circ\):
- Calculate the sine of \(30^\circ\): \( \sin(30^\circ) = 0.5 \).
- Use the formula: \( \text{Area} = \frac{1}{2} \times 7 \times 9 \times 0.5 \).
- Perform the multiplication: \( \text{Area} = \frac{1}{2} \times 31.5 \).
- Divide by 2: \( \text{Area} = 15.75 \text{ cm}^2 \).
This method is efficient and straightforward, especially for triangles where the angle and sides are known. It highlights the power of trigonometry in solving geometric problems.

Formulas for Perimeter of a Triangle
The perimeter of a triangle is the total length of its boundary, calculated by adding the lengths of its sides. Here are the different methods to calculate the perimeter based on the information available:
- Perimeter using Side Lengths (SSS)
If you know the lengths of all three sides (a, b, and c) of the triangle, the perimeter is simply the sum of these sides:
\[
\text{Perimeter} = a + b + c
\] - Perimeter using Two Sides and Included Angle (SAS)
If you know two sides (a and b) and the included angle (\(\gamma\)) between them, you can use the Law of Cosines to find the third side and then calculate the perimeter:
First, find the third side (c) using:
\[
c = \sqrt{a^2 + b^2 - 2ab\cos(\gamma)}
\]Then, the perimeter is:
\[
\text{Perimeter} = a + b + c
\] - Perimeter using Two Angles and One Side (ASA)
If you know two angles (\(\beta\) and \(\gamma\)) and the included side (a), you can use the Law of Sines to find the other two sides and then calculate the perimeter:
First, find the remaining sides (b and c) using:
\[
b = a \frac{\sin(\beta)}{\sin(\alpha)}, \quad c = a \frac{\sin(\gamma)}{\sin(\alpha)}
\]where \(\alpha\) is the third angle, found by:
\[
\alpha = 180^\circ - \beta - \gamma
\]Then, the perimeter is:
\[
\text{Perimeter} = a + b + c
\]
Let's look at some specific cases for better understanding:
- Equilateral Triangle
All sides are equal (a = b = c). The perimeter is:
\[
\text{Perimeter} = 3a
\] - Isosceles Triangle
Two sides are equal (a = b). The perimeter is:
\[
\text{Perimeter} = 2a + c
\] - Right Triangle
One angle is 90 degrees. If the legs are a and b, and the hypotenuse is c, use the Pythagorean Theorem to find c:
\[
c = \sqrt{a^2 + b^2}
\]Then, the perimeter is:
\[
\text{Perimeter} = a + b + c
\]
Perimeter Using Side Lengths
The perimeter of a triangle is the sum of the lengths of its three sides. Calculating the perimeter is straightforward when the side lengths are known. Here’s how to determine the perimeter step-by-step:
- Identify the side lengths: Label the sides of the triangle as \(a\), \(b\), and \(c\). These represent the lengths of the three sides.
- Add the side lengths: The perimeter \(P\) is calculated by summing up the lengths of all three sides. Use the formula: \[ P = a + b + c \]
To illustrate this with an example:
- Suppose you have a triangle with side lengths \(a = 5\), \(b = 7\), and \(c = 10\).
- Plug these values into the formula to find the perimeter: \[ P = 5 + 7 + 10 = 22 \]
Therefore, the perimeter of this triangle is 22 units.
Special Cases
In some types of triangles, the perimeter calculation can be simplified:
- Equilateral Triangle: All sides are equal (\(a = b = c\)).
The formula simplifies to: \[ P = 3a \] For example, if each side is 6 units, then: \[ P = 3 \times 6 = 18 \] - Isosceles Triangle: Two sides are equal (\(a = b\)).
The formula becomes: \[ P = 2a + c \] For example, if the equal sides are 4 units each and the base is 5 units, then: \[ P = 2 \times 4 + 5 = 13 \]
Calculating the perimeter of a triangle is an essential skill in geometry, useful in various applications, from simple measurements to complex constructions.
Special Cases for Perimeter
While the general formula for the perimeter of a triangle is the sum of its side lengths, there are special cases where the calculation becomes simpler due to the triangle's properties. Let's explore these special cases:
1. Equilateral Triangle
An equilateral triangle has all three sides of equal length. If each side is denoted as \( a \), the formula for the perimeter \( P \) is:
-
Formula:
\[
P = 3a
\] -
Example: If each side is 8 units, then:
\[
P = 3 \times 8 = 24 \text{ units}
\]
2. Isosceles Triangle
An isosceles triangle has two sides of equal length. Let the two equal sides be \( a \) and the base be \( b \). The formula for the perimeter \( P \) is:
-
Formula:
\[
P = 2a + b
\] -
Example: If the equal sides are 5 units each and the base is 7 units, then:
\[
P = 2 \times 5 + 7 = 17 \text{ units}
\]
3. Right Triangle
A right triangle has one right angle (90 degrees). If the lengths of the legs are \( a \) and \( b \), and the hypotenuse is \( c \), the perimeter \( P \) is:
-
Formula:
\[
P = a + b + c
\] -
Example: If the legs are 3 units and 4 units, and the hypotenuse (found using the Pythagorean theorem) is 5 units, then:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
These simplified formulas for special cases can make the process of finding the perimeter quicker and easier. Understanding these cases is beneficial for solving geometry problems efficiently.
Step-by-Step Calculation Examples
Example Using Base and Height
Let's find the area of a triangle with a base of 8 cm and a height of 5 cm.
- Write down the formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Substitute the given values: \( \text{Area} = \frac{1}{2} \times 8 \times 5 \)
- Calculate the product: \( \text{Area} = \frac{1}{2} \times 40 \)
- Simplify the result: \( \text{Area} = 20 \, \text{cm}^2 \)
Example Using Heron's Formula
Now, let's find the area of a triangle with sides 6 cm, 8 cm, and 10 cm using Heron's formula.
- First, calculate the semi-perimeter \( s \):
- \( s = \frac{a + b + c}{2} \)
- \( s = \frac{6 + 8 + 10}{2} = 12 \, \text{cm} \)
- Use Heron's formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \)
- Substitute the values: \( \text{Area} = \sqrt{12(12-6)(12-8)(12-10)} \)
- Simplify inside the square root: \( \text{Area} = \sqrt{12 \times 6 \times 4 \times 2} \)
- Calculate the result: \( \text{Area} = \sqrt{576} = 24 \, \text{cm}^2 \)
Example Using Trigonometric Method
For a triangle with sides 7 cm and 9 cm and the included angle of 60°, find the area.
- Write down the formula: \( \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \)
- Substitute the given values: \( \text{Area} = \frac{1}{2} \times 7 \times 9 \times \sin(60^\circ) \)
- Use the sine value: \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \)
- Calculate the product: \( \text{Area} = \frac{1}{2} \times 7 \times 9 \times \frac{\sqrt{3}}{2} \)
- Simplify the result: \( \text{Area} = \frac{63 \sqrt{3}}{4} \approx 27.23 \, \text{cm}^2 \)
Example Using Perimeter Calculation
For a triangle with sides 5 cm, 12 cm, and 13 cm, calculate the perimeter.
- Write down the formula: \( \text{Perimeter} = a + b + c \)
- Substitute the given values: \( \text{Perimeter} = 5 + 12 + 13 \)
- Calculate the result: \( \text{Perimeter} = 30 \, \text{cm} \)

Example Using Base and Height
To find the area of a triangle using the base and height, you can use the following formula:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\]
Let's go through a detailed example step-by-step:
- Identify the base and the height of the triangle:
Consider a triangle with a base \( b = 8 \) units and a height \( h = 5 \) units.
- Plug the values into the formula:
Using the formula:
\[
\text{Area} = \frac{1}{2} \times b \times h
\]
Substituting the given values:
\[
\text{Area} = \frac{1}{2} \times 8 \times 5
\] - Perform the multiplication:
First, multiply the base and height:
\[
8 \times 5 = 40
\] - Divide by 2 to get the area:
Now, divide the result by 2:
\[
\frac{40}{2} = 20
\] - State the final result:
The area of the triangle is \( 20 \) square units.
For better understanding, here's a table summarizing the steps:
| Step | Description | Calculation | Result |
|---|---|---|---|
| 1 | Identify the base and height | \( b = 8 \), \( h = 5 \) | - |
| 2 | Plug the values into the formula | \( \text{Area} = \frac{1}{2} \times 8 \times 5 \) | - |
| 3 | Multiply base and height | \( 8 \times 5 \) | 40 |
| 4 | Divide by 2 | \( \frac{40}{2} \) | 20 |
| 5 | State the final result | - | 20 square units |
Example Using Heron's Formula
Heron's formula allows us to find the area of a triangle when we know the lengths of all three sides. This formula is especially useful for scalene triangles, where all sides have different lengths. Here are the steps to use Heron's formula:
- Calculate the semi-perimeter (s):
- Apply Heron's formula:
The semi-perimeter of a triangle is half of its perimeter. It is calculated as:
\[
s = \frac{a + b + c}{2}
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Using the semi-perimeter, the area \(A\) of the triangle can be calculated as:
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
Let's work through an example:
Example
Consider a triangle with side lengths \(a = 5\) cm, \(b = 6\) cm, and \(c = 7\) cm. Follow these steps to find the area:
- Calculate the semi-perimeter:
- Apply Heron's formula:
\[
s = \frac{5 + 6 + 7}{2} = 9 \text{ cm}
\]
\[
A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)}
\]
Substitute the values:
\[
A = \sqrt{9 \times 4 \times 3 \times 2}
\]
Simplify inside the square root:
\[
A = \sqrt{216}
\]
Approximate the square root:
\[
A \approx 14.7 \text{ cm}^2
\]
Therefore, the area of the triangle with sides 5 cm, 6 cm, and 7 cm is approximately 14.7 square centimeters.
Example Using Trigonometry
To find the area of a triangle using trigonometry, we use the formula that involves two sides and the included angle between them. The formula is given by:
\[ \text{Area} = \frac{1}{2}ab \sin(C) \]
Where \(a\) and \(b\) are the lengths of two sides of the triangle, and \(C\) is the included angle.
Example
Consider a triangle with sides \(a = 7\) cm, \(b = 10\) cm, and the included angle \(C = 30^\circ\). Let's find the area of this triangle step by step.
-
Identify the sides and the included angle:
- Side \(a = 7\) cm
- Side \(b = 10\) cm
- Included angle \(C = 30^\circ\)
Use the trigonometric area formula:
\[
\text{Area} = \frac{1}{2} \times 7 \times 10 \times \sin(30^\circ)
\]-
Calculate the sine of the angle:
\[
\sin(30^\circ) = 0.5
\] -
Substitute the values into the formula:
\[
\text{Area} = \frac{1}{2} \times 7 \times 10 \times 0.5
\] -
Simplify the expression:
\[
\text{Area} = \frac{1}{2} \times 7 \times 5 = 17.5 \text{ cm}^2
\]
Thus, the area of the triangle is 17.5 square centimeters.
Applications of Area and Perimeter in Real Life
The concepts of area and perimeter are fundamental in many real-world scenarios. Here are some key applications:
-
Construction and Architecture:
When designing homes, buildings, and other structures, architects use area and perimeter to determine the layout and the amount of materials needed. For instance, the perimeter is used to measure the boundary length for walls, fences, or wiring, while the area helps in calculating the flooring space, paint needed for walls, and the space available for rooms.
-
Agriculture:
Farmers use area calculations to determine the size of their fields and plan the layout of crops. The perimeter is important for fencing the land to protect the crops from animals and trespassers.
-
Landscaping:
Landscapers use these measurements to design gardens and parks. The area helps in planning the layout of lawns, flower beds, and other features, while the perimeter is useful for placing borders and pathways.
-
Interior Design:
Interior designers calculate the area to determine the size of carpets, the amount of paint required for walls, and the placement of furniture. The perimeter can help in creating efficient and aesthetically pleasing room layouts.
-
Road and Bridge Construction:
Engineers use area and perimeter calculations to design roads and bridges. They help in determining the amount of materials needed and in ensuring the stability and safety of these structures.
-
Navigation and Mapping:
Cartographers use area and perimeter in creating maps. They help in accurately representing geographical regions and in planning routes for travel and transportation.
-
Art and Fashion:
In the art world, area and perimeter are crucial for creating pieces with specific dimensions. Fashion designers also use these measurements to create patterns and ensure proper fitting of clothing.
-
Computer Graphics:
In digital design and animation, area and perimeter calculations help in rendering accurate graphics and animations. They are essential for creating realistic models and environments in video games and simulations.
Understanding these applications demonstrates the importance of mastering the concepts of area and perimeter, as they play a crucial role in various fields and everyday tasks.
Common Mistakes and Tips
Calculating the area and perimeter of a triangle can sometimes be challenging. Here are some common mistakes and tips to avoid them:
Common Mistakes
- Incorrect Formula Usage: Using the wrong formula for a specific type of triangle (e.g., using Heron's formula without verifying if all sides are known).
- Units Mismatch: Not converting all measurements to the same unit before performing calculations. Always ensure that the base, height, and sides are in the same unit.
- Ignoring Perpendicular Height: For the formula \( \frac{1}{2} \times \text{base} \times \text{height} \), the height must be perpendicular to the base.
- Incorrect Application of Heron's Formula: Forgetting to take the square root when using Heron's formula.
- Errors in Trigonometric Calculations: Not using the correct angle or incorrect use of trigonometric functions when using the trigonometric method.
Tips
- Double-Check Formulas: Always ensure you are using the correct formula for the type of triangle you are working with.
- Consistent Units: Always convert all measurements to the same unit before calculating. For example, if the base is in meters and the height in centimeters, convert one so that both are in the same unit.
- Use a Calculator: For complex calculations, especially those involving trigonometric functions, use a scientific calculator to minimize errors.
- Verify Perpendicular Height: Ensure that the height used in the area calculation is perpendicular to the base.
- Practice: Regular practice with different types of triangles and problems can help you become more familiar with the formulas and their correct application.
By being aware of these common mistakes and following these tips, you can improve the accuracy of your calculations and better understand the geometry of triangles.
FAQs about Triangle Calculations
Here are some frequently asked questions about triangle calculations, including formulas for area and perimeter, and how to use them in various scenarios.
- What is the perimeter of a triangle?
- What is the area of a triangle?
- Base and Height Method: \( A = \frac{1}{2} \times \text{base} \times \text{height} \).
- Heron's Formula: \( A = \sqrt{s(s - a)(s - b)(s - c)} \), where \( s = \frac{a + b + c}{2} \).
- Trigonometric Method: \( A = \frac{1}{2}ab \sin(C) \), where \( a \) and \( b \) are sides and \( C \) is the included angle.
- How do you find the third side of a triangle given two sides?
- Can a triangle have the same area and perimeter?
- How do you find the perimeter of a triangle with coordinates?
- \( a = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- \( b = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \)
- \( c = \sqrt{(x_1 - x_3)^2 + (y_1 - y_3)^2} \)
- How do you find the area of an equilateral triangle?
The perimeter of a triangle is the total length of its boundary, which is calculated by adding the lengths of all three sides. The formula is \( P = a + b + c \), where \( a \), \( b \), and \( c \) are the sides of the triangle.
The area of a triangle is the amount of space inside the triangle. There are multiple formulas to calculate the area depending on the known values:
For right triangles, you can use the Pythagorean theorem: \( c^2 = a^2 + b^2 \), where \( c \) is the hypotenuse and \( a \) and \( b \) are the other two sides. For non-right triangles, the law of cosines may be used: \( c^2 = a^2 + b^2 - 2ab\cos(C) \).
Yes, a triangle can have the same numerical value for both area and perimeter in certain cases, known as equable triangles. These shapes are special and occur under specific conditions.
If the vertices of the triangle are given as coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), you can use the distance formula to find the length of each side:
Once you have the side lengths, sum them to find the perimeter: \( P = a + b + c \).
For an equilateral triangle with side length \( a \), the area is given by \( A = \frac{\sqrt{3}}{4}a^2 \).
Hướng dẫn chi tiết cách tính diện tích và chu vi của tam giác. Video này sẽ giúp bạn hiểu rõ các công thức và phương pháp tính toán.
Cách Tìm Diện Tích và Chu Vi của Tam Giác
READ MORE:
Hướng dẫn cách tính diện tích và chu vi của tam giác. Video này sẽ giúp bạn hiểu rõ các công thức và phương pháp tính toán một cách dễ dàng và hiệu quả.
Cách Tìm Diện Tích và Chu Vi của Tam Giác | Toán Học với Thầy J