Topic formula for perimeter and area of a triangle: Discover the essential formulas for calculating the perimeter and area of a triangle. This comprehensive guide will help you understand the basic concepts, different methods, and practical applications, making it easier to solve problems efficiently. Whether you're a student or a math enthusiast, this article is your go-to resource for mastering triangle calculations.
Table of Content
- Formulas for Perimeter and Area of a Triangle
- Introduction
- Basics of Triangles
- Types of Triangles
- Formula for Perimeter
- Examples of Perimeter Calculation
- Formula for Area
- Heron's Formula
- Examples of Area Calculation
- Special Triangle Area Formulas
- Equilateral Triangle Area
- Isosceles Triangle Area
- Right Triangle Area
- Applications of Perimeter and Area Formulas
- Common Mistakes and How to Avoid Them
- Practice Problems
- Conclusion
- YOUTUBE: Hướng dẫn cách tìm diện tích và chu vi tam giác dễ hiểu và chính xác, phù hợp cho học sinh và những người yêu thích toán học.
Formulas for Perimeter and Area of a Triangle
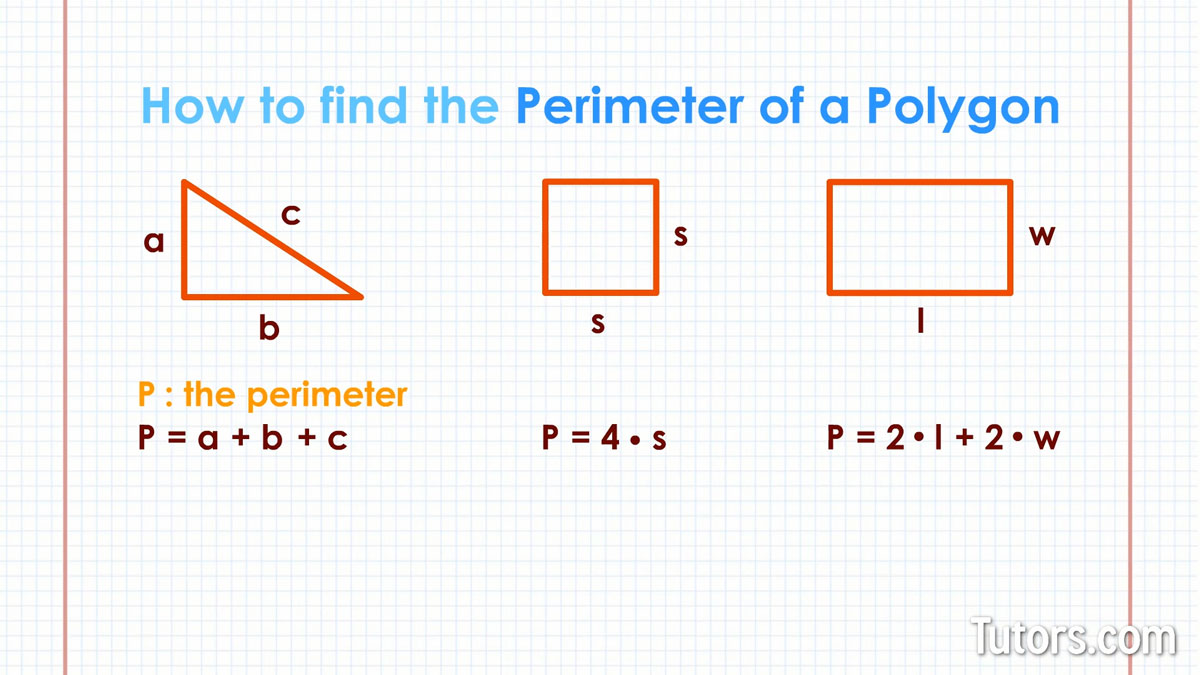
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its three sides. If the sides are labeled as \( a \), \( b \), and \( c \), the formula for the perimeter \( P \) is:
\[ P = a + b + c \]
Area of a Triangle
There are several ways to calculate the area of a triangle depending on the information available. Below are the most commonly used formulas:
1. Using Base and Height
If the base \( b \) and height \( h \) of the triangle are known, the area \( A \) is given by:
\[ A = \frac{1}{2} \times b \times h \]
2. Using Heron's Formula
When the lengths of all three sides \( a \), \( b \), and \( c \) are known, the area can be found using Heron's formula. First, calculate the semi-perimeter \( s \):
\[ s = \frac{a + b + c}{2} \]
Then, the area \( A \) is:
\[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
3. Using Trigonometry
If two sides and the included angle are known, the area can be calculated using the formula:
\[ A = \frac{1}{2} \times a \times b \times \sin(C) \]
where \( a \) and \( b \) are the lengths of the sides, and \( C \) is the included angle.
4. Using Coordinates
If the vertices of the triangle are given as coordinates \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the area can be calculated using the formula:
\[ A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \]
Summary Table
| Perimeter | \[ P = a + b + c \] |
| Area (Base and Height) | \[ A = \frac{1}{2} \times b \times h \] |
| Area (Heron's Formula) | \[ A = \sqrt{s(s - a)(s - b)(s - c)} \] |
| Area (Trigonometry) | \[ A = \frac{1}{2} \times a \times b \times \sin(C) \] |
| Area (Coordinates) | \[ A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \] |

READ MORE:
Introduction
Understanding the formulas for the perimeter and area of a triangle is fundamental in geometry. These formulas are crucial for solving various mathematical problems and have practical applications in fields such as engineering, architecture, and computer graphics. In this section, we will introduce the key concepts and notations used in these calculations, providing a solid foundation for further exploration.
To begin with, let's define a triangle. A triangle is a polygon with three edges and three vertices. The sum of the internal angles in a triangle is always 180 degrees. Triangles can be classified based on their side lengths (scalene, isosceles, and equilateral) or their angles (acute, obtuse, and right).
The perimeter of a triangle is the total length of its three sides. It is calculated using the formula:
\[ \text{Perimeter} = a + b + c \]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
The area of a triangle, on the other hand, can be calculated using different formulas depending on the known parameters. The most common formula is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
where the base is one side of the triangle and the height is the perpendicular distance from the base to the opposite vertex.
For triangles where the height is not known, Heron's formula can be used. Heron's formula requires the lengths of all three sides and is given by:
\[ s = \frac{a + b + c}{2} \]
\[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \]
where \(s\) is the semi-perimeter of the triangle.
In the following sections, we will delve deeper into these formulas, explore special cases, and provide examples to illustrate their application.
Basics of Triangles
A triangle is one of the simplest shapes in geometry, consisting of three sides, three vertices, and three angles. Understanding the basics of triangles is crucial for mastering more complex geometric concepts. Here, we will explore the key properties and types of triangles.
Properties of Triangles
- The sum of the internal angles of a triangle is always \(180^\circ\).
- The length of any side of a triangle is always less than the sum of the other two sides (Triangle Inequality Theorem).
Types of Triangles by Sides
- Scalene Triangle: All three sides and all three angles are different.
- Isosceles Triangle: Has two sides of equal length and two equal angles opposite these sides.
- Equilateral Triangle: All three sides are of equal length, and all three angles are \(60^\circ\).
Types of Triangles by Angles
- Acute Triangle: All three angles are less than \(90^\circ\).
- Obtuse Triangle: One angle is greater than \(90^\circ\).
- Right Triangle: One angle is exactly \(90^\circ\).
Triangle Notations
In a triangle, the sides are usually denoted by lowercase letters \(a\), \(b\), and \(c\), while the opposite angles are denoted by uppercase letters \(A\), \(B\), and \(C\). The vertices of the triangle are typically labeled as \(A\), \(B\), and \(C\).
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its sides. It is calculated using the formula:
\[ \text{Perimeter} = a + b + c \]
Area of a Triangle
The area of a triangle can be calculated using different methods depending on the given information. The most common formula is based on the base and height:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
In cases where the height is not known, Heron's formula can be used, which involves the semi-perimeter (\(s\)) of the triangle:
\[ s = \frac{a + b + c}{2} \]
\[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \]
Understanding these basics provides a strong foundation for solving more complex problems involving triangles. In the following sections, we will delve deeper into specific formulas and examples to further enhance your comprehension.
Types of Triangles
Triangles are classified based on the length of their sides and the measure of their angles. Below are the main types of triangles:
By Sides
- Equilateral Triangle: All three sides are of equal length, and all three angles are equal, each measuring 60 degrees.
- Isosceles Triangle: Two sides are of equal length, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different from each other.
By Angles
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees. The side opposite this angle is called the hypotenuse.
- Obtuse Triangle: One angle is greater than 90 degrees.
Each type of triangle has unique properties and formulas for calculating area and perimeter. Understanding these properties is essential for solving geometric problems effectively.
Formula for Perimeter
The perimeter of a triangle is the total length of its boundary, calculated by summing the lengths of all three sides. Depending on the type of triangle and the information given, different formulas can be used to determine the perimeter.
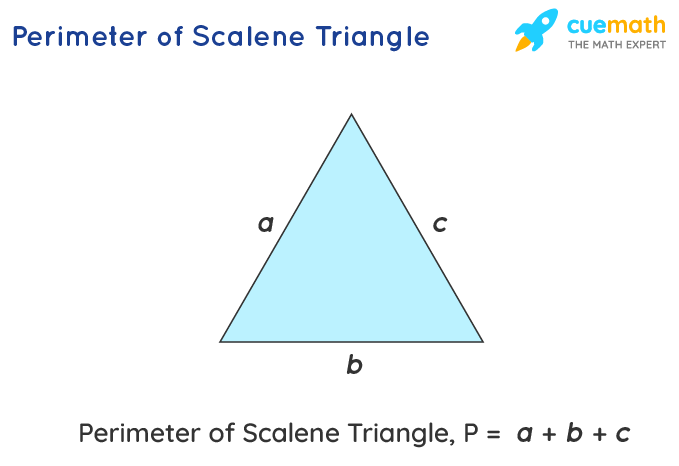
- Scalene Triangle: A triangle with all sides of different lengths.
Formula: \( P = a + b + c \)
Example: For a triangle with sides \( a = 6 \, \text{in}, b = 8 \, \text{in}, \text{and} c = 10 \, \text{in} \), the perimeter is \( P = 6 + 8 + 10 = 24 \, \text{in} \).
- Equilateral Triangle: A triangle with all three sides of equal length.
Formula: \( P = 3a \)
Example: For a triangle with each side \( a = 5 \, \text{in} \), the perimeter is \( P = 3 \times 5 = 15 \, \text{in} \).
- Isosceles Triangle: A triangle with two sides of equal length.
Formula: \( P = 2a + b \)
Example: For a triangle with equal sides \( a = 7 \, \text{in} \) and base \( b = 10 \, \text{in} \), the perimeter is \( P = 2 \times 7 + 10 = 24 \, \text{in} \).
- Right Triangle: A triangle with one \( 90^\circ \) angle.
Using Pythagoras' theorem: \( h = \sqrt{a^2 + b^2} \)
Formula: \( P = a + b + h \)
Example: For a right triangle with legs \( a = 3 \, \text{in} \) and \( b = 4 \, \text{in} \), the hypotenuse \( h = 5 \, \text{in} \) (calculated as \( h = \sqrt{3^2 + 4^2} = 5 \)). The perimeter is \( P = 3 + 4 + 5 = 12 \, \text{in} \).
In cases where only two sides and an included angle (SAS) or two angles and an included side (ASA) are given, the law of cosines or the law of sines can be used to find the missing side(s) and then calculate the perimeter.

Examples of Perimeter Calculation
Here are some examples to help you understand how to calculate the perimeter of different types of triangles:
Example 1: Scalene Triangle
Find the perimeter of a scalene triangle with sides of 5 cm, 7 cm, and 9 cm.
- Note the lengths of all three sides: a = 5 cm, b = 7 cm, c = 9 cm.
- Add the lengths of the sides: \( \text{Perimeter} = a + b + c \).
- Calculate the perimeter: \( \text{Perimeter} = 5 + 7 + 9 = 21 \, \text{cm} \).
Example 2: Equilateral Triangle
Find the perimeter of an equilateral triangle with each side measuring 6 cm.
- Note the length of one side: a = 6 cm.
- Since all sides are equal, multiply the length of one side by 3: \( \text{Perimeter} = 3a \).
- Calculate the perimeter: \( \text{Perimeter} = 3 \times 6 = 18 \, \text{cm} \).
Example 3: Isosceles Triangle
Find the perimeter of an isosceles triangle with two equal sides of 8 cm and a base of 5 cm.
- Note the lengths of the sides: a = 8 cm (two equal sides), b = 5 cm (base).
- Since two sides are equal, use the formula: \( \text{Perimeter} = 2a + b \).
- Calculate the perimeter: \( \text{Perimeter} = 2 \times 8 + 5 = 16 + 5 = 21 \, \text{cm} \).
Example 4: Right Triangle
Find the perimeter of a right triangle with legs measuring 3 inches and 4 inches.
- Note the lengths of the legs: a = 3 inches, b = 4 inches.
- Calculate the hypotenuse using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{inches} \).
- Add the lengths of all sides to find the perimeter: \( \text{Perimeter} = a + b + c \).
- Calculate the perimeter: \( \text{Perimeter} = 3 + 4 + 5 = 12 \, \text{inches} \).
Example 5: Given Perimeter
Find the missing side of a triangle if the perimeter is 48 inches and the two known sides are 17 inches each.
- Let the length of the missing side be \( c \).
- Use the perimeter formula: \( \text{Perimeter} = a + b + c \).
- Substitute the known values: \( 48 = 17 + 17 + c \).
- Solve for the missing side: \( 48 = 34 + c \), hence \( c = 48 - 34 = 14 \, \text{inches} \).
Formula for Area
The area of a triangle can be calculated using several different formulas depending on the information available. Here are the most commonly used formulas:
1. Base and Height Formula
If you know the base and height of the triangle, you can use the following formula:
Area = 1/2 × base × height
In mathematical notation, this is often written as:
Area = \frac{1}{2} \times b \times h
where b is the length of the base, and h is the height perpendicular to the base.
2. Heron's Formula
When you know the lengths of all three sides of the triangle, you can use Heron's formula. First, calculate the semi-perimeter (s) of the triangle:
s = \frac{a + b + c}{2}
Then, use the semi-perimeter to find the area:
Area = \sqrt{s \times (s - a) \times (s - b) \times (s - c)}
where a, b, and c are the lengths of the sides of the triangle.
3. Using Trigonometry
When you know two sides and the included angle, the area can be found using the formula:
Area = \frac{1}{2} \times a \times b \times \sin(C)
where a and b are the lengths of the two sides, and C is the included angle.
4. Special Triangle Area Formulas
For certain types of triangles, specific formulas can simplify the calculation:
- Equilateral Triangle:
Area = \frac{\sqrt{3}}{4} \times a^2, where a is the side length. - Isosceles Triangle: If you know the length of the equal sides and the base, use:
Area = \frac{1}{2} \times base \times \sqrt{side^2 - \frac{base^2}{4}}. - Right Triangle:
Area = \frac{1}{2} \times leg_1 \times leg_2, where the legs are the two perpendicular sides.
5. Coordinate Geometry
If the vertices of the triangle are known on a coordinate plane, you can use the determinant method:
Area = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|
where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the triangle's vertices.
Heron's Formula
Heron's formula allows us to calculate the area of a triangle when we know the lengths of all three sides. This method is especially useful for triangles that do not have a right angle and cannot use simpler area formulas directly.
The formula is attributed to Heron of Alexandria, a Greek engineer and mathematician. It is expressed as:
Step 1: Calculate the semi-perimeter (s)
Given a triangle with side lengths \( a \), \( b \), and \( c \):
\[
s = \frac{a + b + c}{2}
\]
Step 2: Calculate the area (A)
Using the semi-perimeter \( s \) and the side lengths:
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
This formula works for any triangle, provided you know the lengths of all three sides. Here's an example to illustrate the use of Heron's formula:
Example Calculation
Consider a triangle with side lengths \( a = 5 \) units, \( b = 6 \) units, and \( c = 7 \) units:
- First, find the semi-perimeter:
\[
s = \frac{5 + 6 + 7}{2} = 9
\] - Next, apply Heron's formula to find the area:
\[
A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \, \text{square units}
\]
Thus, the area of the triangle is approximately 14.7 square units.
Heron's formula is not only valuable for computing the area of a triangle but also forms the basis for more complex geometric calculations, such as finding the area of a cyclic quadrilateral.
Examples of Area Calculation
Calculating the area of a triangle can be approached in various ways depending on the type of triangle and the given dimensions. Below are several examples demonstrating how to find the area using different formulas.
Example 1: Using Base and Height
Find the area of a triangle with a base of 12 cm and a height of 5 cm.
The formula for the area of a triangle is:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\]
Substituting the given values:
\[
\text{Area} = \frac{1}{2} \times 12 \, \text{cm} \times 5 \, \text{cm} = 30 \, \text{cm}^2
\]
Example 2: Equilateral Triangle
Find the area of an equilateral triangle with each side measuring 8 cm.
The formula for the area of an equilateral triangle is:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2
\]
Substituting the side length:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times (8 \, \text{cm})^2 = 16\sqrt{3} \, \text{cm}^2 \approx 27.71 \, \text{cm}^2
\]
Example 3: Isosceles Triangle
Calculate the area of an isosceles triangle with equal sides of 10 cm each and a base of 12 cm.
Using the formula for the area of an isosceles triangle:
\[
\text{Area} = \frac{1}{2} \times b \times \sqrt{a^2 - \frac{b^2}{4}}
\]
Where \( a \) is the length of the equal sides and \( b \) is the base.
Substituting the given values:
\[
\text{Area} = \frac{1}{2} \times 12 \, \text{cm} \times \sqrt{10^2 - \frac{12^2}{4}} = 60 \, \text{cm}^2
\]
Example 4: Using Heron's Formula
Find the area of a triangle with sides of 7 cm, 8 cm, and 9 cm.
First, calculate the semi-perimeter \( s \):
\[
s = \frac{a + b + c}{2} = \frac{7 \, \text{cm} + 8 \, \text{cm} + 9 \, \text{cm}}{2} = 12 \, \text{cm}
\]
Using Heron's formula:
\[
\text{Area} = \sqrt{s(s - a)(s - b)(s - c)} = \sqrt{12(12 - 7)(12 - 8)(12 - 9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.83 \, \text{cm}^2
\]
Example 5: Right-Angle Triangle
Determine the area of a right-angled triangle with one leg measuring 9 units and the other leg measuring 12 units.
The formula for the area of a right-angled triangle is:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\]
Here, the legs of the triangle serve as the base and height. Substituting the values:
\[
\text{Area} = \frac{1}{2} \times 9 \, \text{units} \times 12 \, \text{units} = 54 \, \text{units}^2
\]
These examples illustrate the application of different formulas for finding the area of various types of triangles.

Special Triangle Area Formulas
Different types of triangles have unique properties that simplify the calculation of their areas. Here, we will explore some special triangle area formulas for equilateral, isosceles, and right triangles.
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula for its area is derived using the side length \( a \).
Area Formula:
\[
\text{Area} = \frac{\sqrt{3}}{4} a^2
\]
For example, if the side length \( a \) is 6 units, then the area \( A \) is:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = 9\sqrt{3} \approx 15.59 \, \text{square units}
\]
Isosceles Triangle
An isosceles triangle has two sides of equal length and a unique base. To find its area, we can use the following formula, where \( b \) is the base and \( h \) is the height:
Area Formula:
\[
\text{Area} = \frac{1}{2} \times b \times h
\]
To find the height, we can use the Pythagorean theorem if the side lengths and base are known. For example, if an isosceles triangle has a base \( b \) of 8 units and equal sides of 10 units, the height \( h \) can be calculated as follows:
\[
h = \sqrt{10^2 - \left(\frac{8}{2}\right)^2} = \sqrt{100 - 16} = \sqrt{84} = 2\sqrt{21} \, \text{units}
\]
Thus, the area \( A \) is:
\[
\text{Area} = \frac{1}{2} \times 8 \times 2\sqrt{21} = 8\sqrt{21} \approx 36.73 \, \text{square units}
\]
Right Triangle
A right triangle has one 90-degree angle. The area can be easily calculated using the two legs of the triangle, which are perpendicular to each other. If \( a \) and \( b \) are the lengths of these legs:
Area Formula:
\[
\text{Area} = \frac{1}{2} \times a \times b
\]
For example, if the legs of a right triangle are 5 units and 12 units, the area \( A \) is:
\[
\text{Area} = \frac{1}{2} \times 5 \times 12 = 30 \, \text{square units}
\]
Special Right Triangles: 30°-60°-90° and 45°-45°-90°
Special right triangles have unique properties that make area calculation straightforward. Here are the formulas:
30°-60°-90° Triangle
The sides of a 30°-60°-90° triangle are in the ratio \( 1 : \sqrt{3} : 2 \). Given the shortest side \( a \), the other sides are \( a\sqrt{3} \) and \( 2a \). The area formula is:
Area Formula:
\[
\text{Area} = \frac{a^2 \sqrt{3}}{4}
\]
For instance, if the shortest side \( a \) is 6 units, the area \( A \) is:
\[
\text{Area} = \frac{6^2 \sqrt{3}}{4} = 9\sqrt{3} \approx 15.59 \, \text{square units}
\]
45°-45°-90° Triangle
The sides of a 45°-45°-90° triangle are in the ratio \( 1 : 1 : \sqrt{2} \). Given one leg \( a \), the other leg is \( a \) and the hypotenuse is \( a\sqrt{2} \). The area formula is:
Area Formula:
\[
\text{Area} = \frac{a^2}{2}
\]
For example, if one leg \( a \) is 5 units, the area \( A \) is:
\[
\text{Area} = \frac{5^2}{2} = 12.5 \, \text{square units}
\]
Equilateral Triangle Area
An equilateral triangle is a special type of triangle where all three sides are of equal length and all three angles are equal to 60 degrees. The formula for the area of an equilateral triangle is derived from its symmetrical properties and can be calculated easily using the length of one of its sides.
The formula for the area \( A \) of an equilateral triangle with side length \( a \) is given by:
\[
\text{Area} = \frac{\sqrt{3}}{4} a^2
\]
Derivation of the Formula
To derive this formula, we can use the following steps:
- Divide the Equilateral Triangle into Two Right Triangles
By drawing an altitude (height) from one vertex to the midpoint of the opposite side, the equilateral triangle is divided into two congruent right triangles.
The altitude creates two 30°-60°-90° triangles, where the sides are in the ratio \( 1 : \sqrt{3} : 2 \).
- Calculate the Height
The height \( h \) of the triangle can be found using the Pythagorean theorem in one of the 30°-60°-90° triangles. Given that the base of the right triangle is \( \frac{a}{2} \) and the hypotenuse is \( a \), the height is:
\[
h = \sqrt{a^2 - \left(\frac{a}{2}\right)^2} = \sqrt{a^2 - \frac{a^2}{4}} = \sqrt{\frac{3a^2}{4}} = \frac{a \sqrt{3}}{2}
\] - Apply the Area Formula
Using the basic formula for the area of a triangle, which is \( \frac{1}{2} \times \text{base} \times \text{height} \), we substitute the base \( a \) and the height \( \frac{a \sqrt{3}}{2} \):
\[
\text{Area} = \frac{1}{2} \times a \times \frac{a \sqrt{3}}{2} = \frac{a^2 \sqrt{3}}{4}
\]
Example Calculation
Let's find the area of an equilateral triangle with each side measuring 10 units.
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 10^2 = \frac{\sqrt{3}}{4} \times 100 = 25\sqrt{3} \approx 43.30 \, \text{square units}
\]
Therefore, the area of an equilateral triangle with a side length of 10 units is approximately 43.30 square units.
This formula provides a quick and efficient way to calculate the area of an equilateral triangle, leveraging its unique geometric properties.
Isosceles Triangle Area
An isosceles triangle is a triangle with at least two sides of equal length. These equal sides are called the legs, and the third side is called the base. The area of an isosceles triangle can be calculated using various methods, depending on the information available about the triangle.
Area Formula Using Base and Height
The most straightforward way to calculate the area of an isosceles triangle is by using the base \( b \) and the height \( h \), which is the perpendicular distance from the base to the opposite vertex.
Area Formula:
\[
\text{Area} = \frac{1}{2} \times b \times h
\]
For example, if the base \( b \) is 8 units and the height \( h \) is 5 units, the area \( A \) is:
\[
\text{Area} = \frac{1}{2} \times 8 \times 5 = 20 \, \text{square units}
\]
Calculating Height Using the Pythagorean Theorem
If the height is not directly given, but the lengths of the legs \( l \) and the base \( b \) are known, we can calculate the height using the Pythagorean theorem. The height \( h \) splits the isosceles triangle into two congruent right triangles, each having a base of \( \frac{b}{2} \) and a hypotenuse of \( l \).
The height \( h \) can be found as follows:
\[
h = \sqrt{l^2 - \left(\frac{b}{2}\right)^2}
\]
For example, if the legs \( l \) are 10 units each and the base \( b \) is 12 units, the height \( h \) is:
\[
h = \sqrt{10^2 - \left(\frac{12}{2}\right)^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \, \text{units}
\]
Once the height is known, the area \( A \) is calculated as:
\[
\text{Area} = \frac{1}{2} \times 12 \times 8 = 48 \, \text{square units}
\]
Area Formula Using Side Lengths (Heron's Formula)
Alternatively, if the side lengths are known but the height is not, we can use Heron's formula to find the area. For an isosceles triangle with equal sides \( l \) and base \( b \), Heron's formula involves the semi-perimeter \( s \), which is calculated as:
\[
s = \frac{2l + b}{2}
\]
The area \( A \) is then given by:
\[
\text{Area} = \sqrt{s(s - l)(s - l)(s - b)}
\]
For example, if the side lengths are \( l = 7 \) units and \( b = 10 \) units, the semi-perimeter \( s \) is:
\[
s = \frac{2 \times 7 + 10}{2} = 12 \, \text{units}
\]
Then, the area \( A \) is:
\[
\text{Area} = \sqrt{12(12 - 7)(12 - 7)(12 - 10)} = \sqrt{12 \times 5 \times 5 \times 2} = \sqrt{600} = 10\sqrt{6} \approx 24.49 \, \text{square units}
\]
Conclusion
There are multiple methods to calculate the area of an isosceles triangle, each suited to different sets of given information. Whether using the base and height directly, or deriving the height via the Pythagorean theorem or using Heron's formula, understanding these approaches provides flexibility in solving for the area.
Right Triangle Area
A right triangle is a triangle in which one of the angles is exactly 90 degrees. This unique property allows for straightforward area calculations using the lengths of the legs, which are the two sides that form the right angle.
Basic Area Formula
The most common way to calculate the area of a right triangle is by using its legs. Let \( a \) and \( b \) be the lengths of the legs, then the area \( A \) is given by:
\[
\text{Area} = \frac{1}{2} \times a \times b
\]
For example, if the legs \( a \) and \( b \) are 6 units and 8 units respectively, the area \( A \) is:
\[
\text{Area} = \frac{1}{2} \times 6 \times 8 = 24 \, \text{square units}
\]
Using the Hypotenuse
In a right triangle, the hypotenuse \( c \) is the side opposite the right angle and is the longest side. If the lengths of the hypotenuse and one leg are known, the length of the other leg can be calculated using the Pythagorean theorem:
\[
c^2 = a^2 + b^2
\]
Rearranging to solve for the unknown leg \( b \) when \( a \) and \( c \) are known:
\[
b = \sqrt{c^2 - a^2}
\]
Once both legs are known, the area can be calculated using the basic area formula. For example, if the hypotenuse \( c \) is 13 units and one leg \( a \) is 5 units, the other leg \( b \) is:
\[
b = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \, \text{units}
\]
The area \( A \) is then:
\[
\text{Area} = \frac{1}{2} \times 5 \times 12 = 30 \, \text{square units}
\]
Special Right Triangles
There are two common types of special right triangles with known ratios between their sides:
45°-45°-90° Triangle
In a 45°-45°-90° triangle, the legs are equal in length. If the length of each leg is \( a \), the hypotenuse is \( a\sqrt{2} \). The area formula for this triangle is:
\[
\text{Area} = \frac{1}{2} \times a \times a = \frac{a^2}{2}
\]
For example, if each leg \( a \) is 7 units, the area \( A \) is:
\[
\text{Area} = \frac{7^2}{2} = \frac{49}{2} = 24.5 \, \text{square units}
\]
30°-60°-90° Triangle
In a 30°-60°-90° triangle, the sides are in the ratio \( 1 : \sqrt{3} : 2 \). If the shortest side opposite the 30° angle is \( a \), the hypotenuse is \( 2a \), and the longer leg opposite the 60° angle is \( a\sqrt{3} \). The area formula is:
\[
\text{Area} = \frac{1}{2} \times a \times a\sqrt{3} = \frac{a^2 \sqrt{3}}{2}
\]
For example, if the shortest side \( a \) is 4 units, the area \( A \) is:
\[
\text{Area} = \frac{4^2 \sqrt{3}}{2} = 8\sqrt{3} \approx 13.86 \, \text{square units}
\]
Conclusion
The area of a right triangle can be easily calculated using the lengths of its legs. Special right triangles with known ratios allow for quick and efficient area calculations. Understanding these methods simplifies solving for the area of right triangles in various scenarios.

Applications of Perimeter and Area Formulas
The formulas for the perimeter and area of a triangle are fundamental tools in various fields of science, engineering, architecture, and daily life. Understanding how to apply these formulas can provide significant benefits in practical and theoretical contexts.
1. Architectural Design and Construction
In architecture and construction, calculating the area and perimeter of triangular spaces helps in designing buildings and structures:
- Land Plot Measurement: Surveyors use area and perimeter calculations to determine the dimensions and boundaries of land plots, which are often triangular.
- Roof Design: Many roofs are designed in triangular sections. Knowing the area helps in estimating the amount of roofing material required, while the perimeter is useful for calculating the length of the edges for gutters or framing.
- Structural Integrity: Engineers use these formulas to assess the load distribution and strength of triangular components in trusses and frames.
2. Engineering and Mechanics
In engineering, the principles of perimeter and area are crucial for designing and analyzing structures and mechanical components:
- Force Distribution: Triangular shapes are often used in bridges and frameworks to evenly distribute forces. Calculating the area helps in understanding how forces spread across surfaces.
- Material Usage: Determining the area of triangular sections in materials can optimize the amount used, minimizing waste in manufacturing processes.
- Aerodynamics: Triangular shapes are prevalent in the design of components like wings and fins. The area calculation aids in evaluating aerodynamic properties such as lift and drag.
3. Geographical and Environmental Studies
Geographers and environmental scientists use perimeter and area calculations for various analytical purposes:
- Mapping and Land Use: Calculating the area of triangular sections on maps helps in land use planning and resource management.
- Watershed Analysis: Understanding the area and perimeter of triangular land sections assists in studying water flow and watershed management.
- Environmental Impact: Estimating the area affected by triangular-shaped environmental features, like mountain slopes or forest patches, is crucial for impact assessments.
4. Sports and Recreation
In sports, the principles of triangle area and perimeter are used to design and measure various play areas:
- Field and Court Design: Many sports fields and courts have triangular components. Calculating their area ensures accurate dimensions and optimal use of space.
- Race Track Layouts: Triangular sections in race tracks or swimming pools require precise measurements for fair competition and safety.
- Recreational Planning: Triangular park sections or hiking paths are planned using these formulas to maximize space and accessibility.
5. Everyday Practical Uses
Understanding triangle perimeter and area is beneficial in everyday activities and problem-solving:
- DIY Projects: Home improvement tasks like tiling, flooring, or painting often involve triangular areas. Accurate calculations help in material estimation and cost planning.
- Gardening and Landscaping: Triangular garden beds or landscape features require area calculations to determine soil, mulch, or plant quantities.
- Fashion and Textile: Designing and cutting triangular patterns for clothing or crafts involve precise area and perimeter measurements to ensure proper fit and design.
The applications of triangle perimeter and area formulas are vast and varied, spanning professional fields and everyday life. Mastery of these concepts enhances problem-solving capabilities and supports a wide range of practical and creative endeavors.
Common Mistakes and How to Avoid Them
When calculating the perimeter and area of a triangle, it's easy to make errors. Understanding these common mistakes and learning how to avoid them can ensure accurate and efficient problem-solving.
1. Confusing Perimeter and Area
Mistake: Perimeter and area are often confused. The perimeter is the total length around the triangle, while the area is the space enclosed within the triangle.
- Avoidance Tip: Remember that the perimeter is a linear measure (sum of the side lengths), and the area is a square measure (space inside). Double-check units: perimeter uses linear units (e.g., meters), and area uses square units (e.g., square meters).
2. Incorrect Formula Usage
Mistake: Using the wrong formula for the type of triangle or the given information can lead to incorrect results.
- Avoidance Tip: Verify the triangle type and the information provided (sides, angles, height). Use specific formulas for different triangles, such as:
- For right triangles: \(\text{Area} = \frac{1}{2} \times \text{leg}_1 \times \text{leg}_2\)
- For equilateral triangles: \(\text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2\)
- For any triangle using Heron's formula: \(\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}\), where \(s\) is the semi-perimeter.
3. Misidentifying Triangle Sides
Mistake: Confusing the legs and hypotenuse in a right triangle or the base and height in any triangle can lead to incorrect area calculations.
- Avoidance Tip: Clearly label and identify each side. For right triangles, the hypotenuse is the longest side opposite the right angle. In general triangles, the base is any chosen side, and the height is the perpendicular distance from the base to the opposite vertex.
4. Incorrect Calculation of Height
Mistake: Calculating the height incorrectly when it's not directly given can lead to errors in area calculations.
- Avoidance Tip: Use the Pythagorean theorem to find the height in right and isosceles triangles or apply trigonometric relationships in other triangles. Always ensure the height is perpendicular to the chosen base.
5. Forgetting to Divide by Two
Mistake: Forgetting the division by two in the area formula for triangles can result in an overestimation of the area.
- Avoidance Tip: Remember that the area of a triangle is always half the product of its base and height: \(\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}\). Recheck the formula and your calculations to ensure the division by two is included.
6. Miscalculating the Semi-Perimeter in Heron's Formula
Mistake: Errors in computing the semi-perimeter \( s \) in Heron's formula can lead to incorrect area results.
- Avoidance Tip: The semi-perimeter \( s \) is calculated as \( s = \frac{a + b + c}{2} \). Carefully sum the side lengths and divide by two before substituting into Heron's formula.
7. Misinterpreting Units and Measurements
Mistake: Using inconsistent or incorrect units can cause significant errors in perimeter and area calculations.
- Avoidance Tip: Ensure all measurements are in the same units before performing calculations. Convert units if necessary and be consistent with the unit of measure throughout the problem.
8. Neglecting to Verify Triangle Validity
Mistake: Failing to confirm that a given set of side lengths can form a valid triangle can lead to errors in calculations.
- Avoidance Tip: Use the triangle inequality theorem: for any triangle with sides \( a \), \( b \), and \( c \), the sum of any two sides must be greater than the third side \((a + b > c, a + c > b, b + c > a)\). Ensure the side lengths satisfy this condition before proceeding.
Conclusion
Awareness of these common mistakes and following the provided tips can help you accurately calculate the perimeter and area of triangles. Always double-check your work, use the correct formulas, and be mindful of units and measurements to avoid errors.
Practice Problems
Below are some practice problems to help you understand the concepts of calculating the perimeter and area of various types of triangles. Follow the steps and use the formulas provided to solve each problem.
Problem 1: Perimeter of a Triangle
Given a triangle with sides of lengths 5 cm, 7 cm, and 10 cm, calculate the perimeter.
- Identify the lengths of all three sides: a = 5 cm, b = 7 cm, c = 10 cm.
- Use the perimeter formula: \( P = a + b + c \).
- Substitute the given values: \( P = 5 + 7 + 10 \).
- Calculate the sum: \( P = 22 \) cm.
Problem 2: Area of a Right Triangle
Given a right triangle with base 6 cm and height 8 cm, find the area.
- Identify the base and height: base = 6 cm, height = 8 cm.
- Use the area formula: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \).
- Substitute the values: \( \text{Area} = \frac{1}{2} \times 6 \times 8 \).
- Calculate the product: \( \text{Area} = \frac{1}{2} \times 48 \).
- Simplify the result: \( \text{Area} = 24 \) square cm.
Problem 3: Area of an Equilateral Triangle
Given an equilateral triangle with each side measuring 10 cm, calculate the area.
- Identify the side length: \( s = 10 \) cm.
- Use the area formula for an equilateral triangle: \( \text{Area} = \frac{\sqrt{3}}{4} \times s^2 \).
- Substitute the side length: \( \text{Area} = \frac{\sqrt{3}}{4} \times 10^2 \).
- Calculate the square of the side length: \( 10^2 = 100 \).
- Compute the area: \( \text{Area} = \frac{\sqrt{3} \times 100}{4} = 25\sqrt{3} \) square cm.
Problem 4: Area Using Heron's Formula
Given a triangle with sides of lengths 8 cm, 15 cm, and 17 cm, find the area using Heron's formula.
- Identify the side lengths: a = 8 cm, b = 15 cm, c = 17 cm.
- Calculate the semi-perimeter: \( s = \frac{a + b + c}{2} = \frac{8 + 15 + 17}{2} = 20 \) cm.
- Use Heron's formula: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \).
- Substitute the values: \( \text{Area} = \sqrt{20(20-8)(20-15)(20-17)} \).
- Simplify inside the square root: \( \text{Area} = \sqrt{20 \times 12 \times 5 \times 3} \).
- Calculate the product: \( \text{Area} = \sqrt{3600} = 60 \) square cm.
Problem 5: Finding the Missing Side
If the perimeter of a triangle is 32 units, its area is 35.8 square units, and two sides are 14 units and 12 units, find the length of the third side.
- Calculate the semi-perimeter: \( s = \frac{32}{2} = 16 \) units.
- Use Heron's formula with the known area to set up the equation: \( 35.8 = \sqrt{16(16-14)(16-12)(16-x)} \).
- Simplify and solve for the missing side \( x \).
Conclusion
Understanding the formulas for the perimeter and area of a triangle is essential for grasping basic geometry concepts. These formulas not only help in solving mathematical problems but also have practical applications in various fields such as engineering, architecture, and art. Here are the key takeaways:
- The perimeter of a triangle is the sum of the lengths of its sides: \( P = a + b + c \).
- The area of a triangle can be calculated using several methods:
- The basic formula using base and height: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \).
- Heron's formula for triangles with known side lengths: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \) where \( s = \frac{a + b + c}{2} \).
- Special formulas for specific types of triangles, such as equilateral and isosceles triangles.
Throughout our exploration, we have seen that triangles, though seemingly simple, offer a wealth of interesting properties and applications. Whether it’s calculating the area for construction projects or understanding the geometry behind various designs, triangles play a crucial role.
Remember, mastering these formulas is not just about memorizing them, but understanding their derivations and applications. This knowledge will enhance your mathematical problem-solving skills and appreciation for geometry.
Keep practicing with different types of triangles and problem scenarios to strengthen your understanding. Math is a journey, and with every problem you solve, you are sharpening your skills and expanding your knowledge.
Thank you for following along in this journey through the perimeter and area of triangles. We hope you found this guide informative and engaging. Keep exploring the world of mathematics with curiosity and enthusiasm!
Hướng dẫn cách tìm diện tích và chu vi tam giác dễ hiểu và chính xác, phù hợp cho học sinh và những người yêu thích toán học.
Cách Tìm Diện Tích và Chu Vi Tam Giác | Toán với Mr. J
READ MORE:
Hướng dẫn cách tìm diện tích và chu vi tam giác một cách dễ hiểu và chính xác, phù hợp cho học sinh và người yêu thích toán học.
Cách Tìm Diện Tích và Chu Vi Tam Giác