Topic find perimeter of a triangle: Discover how to find the perimeter of a triangle effortlessly with our comprehensive guide. Learn the formulas and methods for different types of triangles, explore step-by-step examples, and apply these techniques to solve real-world problems. Whether you're a student or a math enthusiast, this article will make calculating triangle perimeters easy and enjoyable.
Table of Content
- Finding the Perimeter of a Triangle
- Introduction
- Basic Definition
- General Formula for Perimeter
- Perimeter of Different Types of Triangles
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
- Examples and Step-by-Step Calculations
- Using Coordinates to Find Perimeter
- Distance Formula
- Application in Coordinate Geometry
- Perimeter in Real-World Problems
- Practical Applications
- Common Mistakes to Avoid
- YOUTUBE: Hướng dẫn tìm chu vi tam giác với video 'Cách Tìm Chu Vi Tam Giác'. Thích hợp cho bài viết về tìm chu vi tam giác.
Finding the Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its sides. It is a fundamental concept in geometry and can be calculated easily if the lengths of all three sides are known. Below are the detailed methods for finding the perimeter of different types of triangles.
General Formula
For any triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is given by:
Example
Suppose we have a triangle with sides of lengths 3 cm, 4 cm, and 5 cm. The perimeter of this triangle is calculated as follows:
Perimeter of Special Triangles
- Equilateral Triangle: For an equilateral triangle with side length \( s \), the perimeter \( P \) is given by:
- Isosceles Triangle: For an isosceles triangle with two equal sides of length \( a \) and base \( b \), the perimeter \( P \) is:
Using Coordinates
If the vertices of the triangle are given in the coordinate plane as \( (x_1, y_1) \), \( (x_2, y_2) \), and \( (x_3, y_3) \), the lengths of the sides can be calculated using the distance formula:
Once the lengths of the sides are determined, the perimeter can be calculated using the general formula.
Conclusion
Finding the perimeter of a triangle is a straightforward process, whether you are dealing with a simple geometric figure or one defined by coordinates. By understanding the basic principles and formulas, you can easily determine the perimeter of any triangle.

READ MORE:
Introduction
Understanding how to find the perimeter of a triangle is a fundamental skill in geometry that applies to various fields such as architecture, engineering, and everyday problem-solving. The perimeter of a triangle is the total length around the triangle, which is the sum of the lengths of its three sides.
Here's a step-by-step guide to finding the perimeter of different types of triangles:
- Identify the type of triangle:
- Equilateral Triangle: All three sides are of equal length.
- Isosceles Triangle: Two sides are of equal length.
- Scalene Triangle: All sides are of different lengths.
- Measure the lengths of the sides: Use a ruler or given measurements to determine the lengths of each side of the triangle.
- Apply the general formula: For any triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is calculated as:
By following these steps, you can easily determine the perimeter of any triangle, enhancing your understanding and application of geometric principles.
Basic Definition
The perimeter of a triangle is a fundamental concept in geometry, representing the total length of the triangle's boundary. It is calculated by adding together the lengths of all three sides of the triangle.
To understand the perimeter of a triangle, follow these steps:
- Identify the sides of the triangle: Each triangle has three sides, usually denoted as \( a \), \( b \), and \( c \).
- Measure the lengths of the sides: Use a ruler or any given measurements to find the lengths of each side.
- Apply the perimeter formula: The general formula for the perimeter \( P \) of a triangle is:
For example, if a triangle has sides of lengths 5 cm, 7 cm, and 10 cm, the perimeter is calculated as follows:
Understanding the basic definition of the perimeter of a triangle is crucial for solving more complex geometric problems and for practical applications in various fields.
General Formula for Perimeter
The general formula for the perimeter of a triangle is straightforward and easy to apply. The perimeter \( P \) is the total distance around the triangle, which is the sum of the lengths of its three sides. Here's how to calculate it:
- Identify the sides of the triangle: Each triangle has three sides, commonly labeled as \( a \), \( b \), and \( c \).
- Measure the lengths of the sides: Use a ruler or the given dimensions to find the lengths of \( a \), \( b \), and \( c \).
- Apply the perimeter formula: The general formula for the perimeter \( P \) is:
Let's break it down with an example:
Suppose you have a triangle with side lengths of 6 cm, 8 cm, and 10 cm. To find the perimeter, follow these steps:
- Identify the sides: \( a = 6 \, \text{cm} \), \( b = 8 \, \text{cm} \), \( c = 10 \, \text{cm} \).
- Measure the lengths: The lengths are given as \( 6 \, \text{cm} \), \( 8 \, \text{cm} \), and \( 10 \, \text{cm} \).
- Apply the formula:
Therefore, the perimeter of the triangle is \( 24 \, \text{cm} \). This formula is universal and works for any triangle, regardless of its type or size, as long as the side lengths are known.
Perimeter of Different Types of Triangles
Triangles come in various types, each with unique properties. The formula for the perimeter remains the same, but knowing the type of triangle helps in understanding the specific characteristics. Here are the different types of triangles and how to find their perimeters:
Equilateral Triangle
An equilateral triangle has all three sides of equal length.
- Identify the side length: Let the side length be \( s \).
- Apply the formula: The perimeter \( P \) is:
For example, if each side of the equilateral triangle is 5 cm, the perimeter is:
Isosceles Triangle
An isosceles triangle has two sides of equal length.
- Identify the side lengths: Let the two equal sides be \( a \) and the base be \( b \).
- Apply the formula: The perimeter \( P \) is:
For example, if the equal sides are 7 cm each and the base is 5 cm, the perimeter is:
Scalene Triangle
A scalene triangle has all sides of different lengths.
- Identify the side lengths: Let the sides be \( a \), \( b \), and \( c \).
- Apply the formula: The perimeter \( P \) is:
For example, if the sides of the scalene triangle are 6 cm, 8 cm, and 10 cm, the perimeter is:
Understanding the specific properties of each type of triangle helps in applying the correct method to find the perimeter, making geometric calculations more intuitive and accurate.
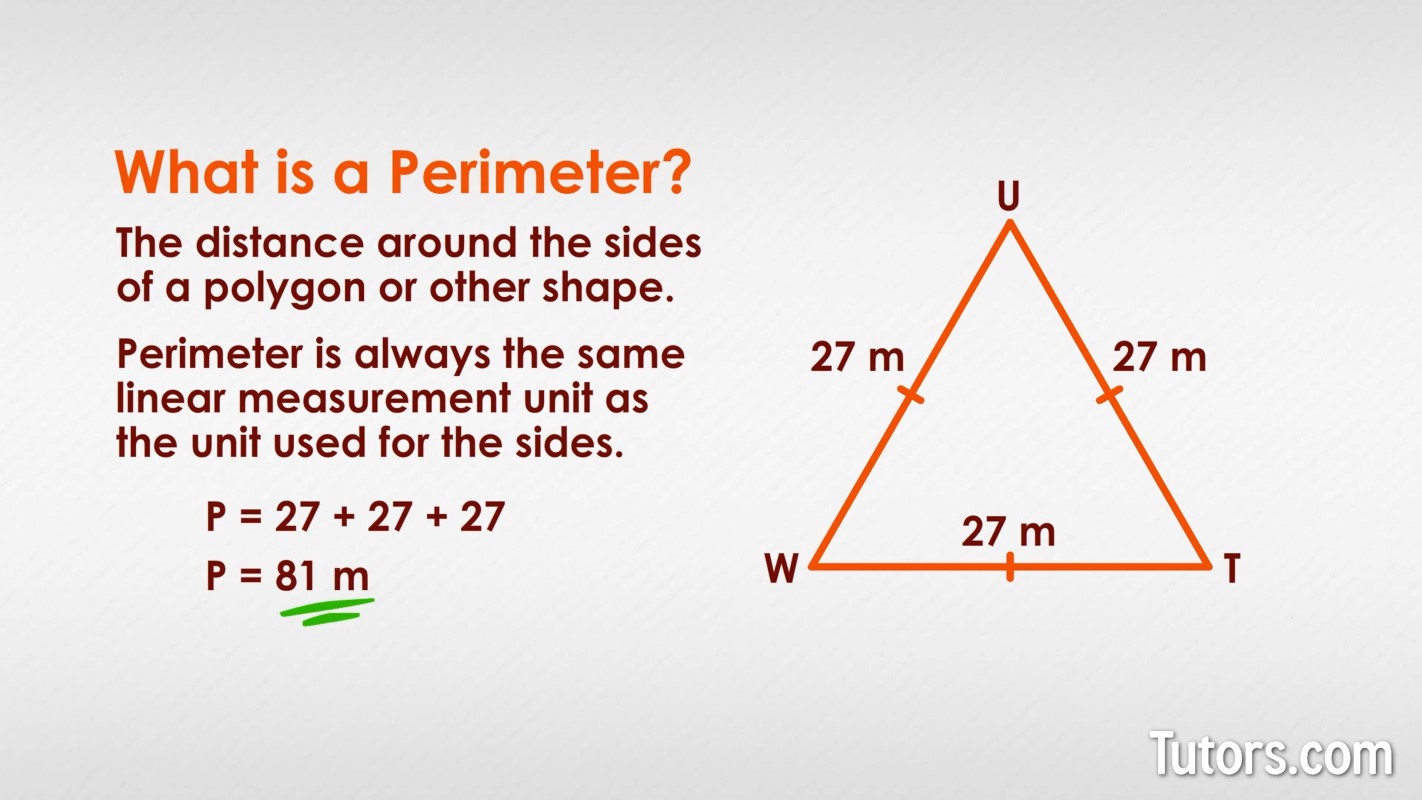
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides are of equal length. This type of triangle is highly symmetrical and has several unique properties.
Properties of an Equilateral Triangle
- All three sides are equal: \( a = b = c \).
- All three interior angles are equal and each measures 60 degrees: \( \angle A = \angle B = \angle C = 60^\circ \).
Formula to Find the Perimeter
The perimeter of an equilateral triangle can be found using the formula:
\[ \text{Perimeter} = 3 \times \text{side length} \]
Step-by-Step Calculation
- Measure the length of one side of the equilateral triangle. Let's denote this length as \( a \).
- Multiply the length of the side by 3.
- The result is the perimeter of the equilateral triangle.
Example
Let's calculate the perimeter of an equilateral triangle with each side measuring 5 cm.
- Side length \( a = 5 \) cm.
- Using the formula: \[ \text{Perimeter} = 3 \times 5 \]
- Calculate the result: \[ \text{Perimeter} = 15 \, \text{cm} \]
Visual Representation
The following diagram shows an equilateral triangle with side length \( a \):

|
In this diagram, you can see that all sides are equal, and each angle is 60 degrees.
Key Takeaways
- All sides and angles in an equilateral triangle are equal.
- The formula for the perimeter is straightforward and involves multiplying the side length by 3.
- This type of triangle is often used in problems and applications due to its symmetry and simplicity.
Isosceles Triangle
An isosceles triangle is a type of triangle that has at least two sides of equal length. These equal sides are known as the legs, and the third side is referred to as the base. The angles opposite the equal sides are also equal.
Properties of an Isosceles Triangle
- Two sides are of equal length.
- The angles opposite the equal sides are equal.
- The altitude drawn from the vertex angle bisects the base and the vertex angle.
- The bisector of the vertex angle is also the median and the altitude of the triangle.
Formula for the Perimeter
The perimeter of an isosceles triangle can be calculated using the following formula:
\[ P = 2a + b \]
where \( a \) is the length of each of the two equal sides, and \( b \) is the length of the base.
Example Calculation
Given an isosceles triangle with each equal side \( a = 5 \) cm and base \( b = 7 \) cm:
- Calculate the perimeter using the formula:
- \[ P = 2a + b = 2(5) + 7 = 10 + 7 = 17 \text{ cm} \]
Altitude of an Isosceles Triangle
The altitude of an isosceles triangle can be found using the Pythagorean theorem. If the equal sides are \( a \) and the base is \( b \), the altitude \( h \) is given by:
\[ h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \]
Example Calculation
Given an isosceles triangle with each equal side \( a = 5 \) cm and base \( b = 4 \) cm:
- Calculate the altitude using the formula:
- \[ h = \sqrt{5^2 - \left(\frac{4}{2}\right)^2} = \sqrt{25 - 4} = \sqrt{21} \approx 4.58 \text{ cm} \]
Applications
- Isosceles triangles are used in architecture and engineering for their symmetry and aesthetic properties.
- They are also used in various proofs and problems in geometry due to their unique properties.
Common Mistakes to Avoid
- Confusing the base with the equal sides. Remember that the base is the side that is not equal to the other two sides.
- Forgetting that the angles opposite the equal sides are equal.
- Not using the correct formula for the perimeter or altitude calculations.
Scalene Triangle
A scalene triangle is a type of triangle where all three sides have different lengths, and all three angles are also different. This lack of symmetry makes scalene triangles unique compared to other types of triangles like equilateral and isosceles triangles.
Properties of a Scalene Triangle
- All sides are of different lengths.
- All angles are of different measures.
- The sum of the internal angles is always 180 degrees.
Perimeter of a Scalene Triangle
The perimeter of a scalene triangle is calculated by adding the lengths of all its sides. If the sides are denoted as \( a \), \( b \), and \( c \), the formula for the perimeter \( P \) is:
\[ P = a + b + c \]
Example Calculation
Consider a scalene triangle with sides of lengths 8 cm, 10 cm, and 12 cm. The perimeter is calculated as follows:
\[ P = 8 \, \text{cm} + 10 \, \text{cm} + 12 \, \text{cm} = 30 \, \text{cm} \]
Area of a Scalene Triangle
The area of a scalene triangle can be calculated using Heron's formula if the lengths of all three sides are known. The steps to use Heron's formula are:
- Calculate the semi-perimeter \( s \) using the formula: \[ s = \frac{a + b + c}{2} \]
- Use the semi-perimeter to find the area \( A \): \[ A = \sqrt{s(s-a)(s-b)(s-c)} \]
Example Calculation Using Heron's Formula
Consider a scalene triangle with sides 7 units, 9 units, and 12 units. To find the area:
- Calculate the semi-perimeter: \[ s = \frac{7 + 9 + 12}{2} = 14 \, \text{units} \]
- Use Heron's formula: \[ A = \sqrt{14(14-7)(14-9)(14-12)} = \sqrt{14 \times 7 \times 5 \times 2} = \sqrt{980} \approx 31.3 \, \text{units}^2 \]
Special Case: Using Base and Height
If the base \( b \) and height \( h \) of the scalene triangle are known, the area can also be calculated using the formula:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
For example, if a scalene triangle has a base of 10 cm and a height of 6 cm, the area is:
\[ \text{Area} = \frac{1}{2} \times 10 \, \text{cm} \times 6 \, \text{cm} = 30 \, \text{cm}^2 \]
Applications of Scalene Triangles
- Engineering and construction for structural analysis.
- Trigonometry problems in mathematics.
- Various real-world applications where non-uniform triangular shapes are needed.
Examples and Step-by-Step Calculations
Understanding how to find the perimeter of different types of triangles can be greatly enhanced with detailed examples and step-by-step calculations. Below are several examples demonstrating how to calculate the perimeter of various triangles.
Example 1: Equilateral Triangle
An equilateral triangle has all three sides of equal length. Let's calculate the perimeter of an equilateral triangle with each side measuring 5 cm.
- Identify the length of one side of the triangle: a = 5 cm.
- Use the perimeter formula for an equilateral triangle: P = 3a.
- Substitute the side length into the formula: P = 3 \times 5.
- Calculate the perimeter: P = 15 cm.
Example 2: Isosceles Triangle
An isosceles triangle has two sides of equal length. Let's find the perimeter of an isosceles triangle with the two equal sides measuring 7 cm each and the base measuring 5 cm.
- Identify the lengths of the sides: a = 5 cm (base), b = 7 cm (equal sides).
- Use the perimeter formula for an isosceles triangle: P = a + 2b.
- Substitute the side lengths into the formula: P = 5 + 2 \times 7.
- Calculate the perimeter: P = 5 + 14 = 19 cm.
Example 3: Scalene Triangle
A scalene triangle has all sides of different lengths. Let's calculate the perimeter of a scalene triangle with sides measuring 4 cm, 6 cm, and 8 cm.
- Identify the lengths of the sides: a = 4 cm, b = 6 cm, c = 8 cm.
- Use the perimeter formula for a scalene triangle: P = a + b + c.
- Substitute the side lengths into the formula: P = 4 + 6 + 8.
- Calculate the perimeter: P = 18 cm.
Example 4: Using Coordinates
To find the perimeter of a triangle when the vertices are given in coordinates, use the distance formula to calculate the length of each side. Consider a triangle with vertices at A(1,2), B(4,6), and C(6,2).
- Calculate the length of side AB using the distance formula:
- AB = \sqrt{(x2 - x1)^2 + (y2 - y1)^2}
- AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5
- Calculate the length of side BC:
- BC = \sqrt{(6 - 4)^2 + (2 - 6)^2} = \sqrt{4 + 16} = \sqrt{20} = 4.47
- Calculate the length of side CA:
- CA = \sqrt{(6 - 1)^2 + (2 - 2)^2} = \sqrt{25 + 0} = \sqrt{25} = 5
- Add the lengths to find the perimeter: P = 5 + 4.47 + 5 = 14.47
Example 5: Right Triangle
For a right triangle with legs measuring 3 inches and 4 inches, and the hypotenuse not given:
- Calculate the hypotenuse using the Pythagorean theorem: c = \sqrt{a^2 + b^2}.
- Substitute the lengths of the legs: c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5.
- Calculate the perimeter: P = a + b + c = 3 + 4 + 5 = 12 inches.
Practice Problem
Find the perimeter of a triangle with sides measuring 5 cm, 12 cm, and 13 cm. Follow the steps demonstrated above to calculate the perimeter.

Using Coordinates to Find Perimeter
To find the perimeter of a triangle when given the coordinates of its vertices, you can use the distance formula to calculate the length of each side and then sum these lengths. Here's a detailed step-by-step guide:
- Identify the coordinates of the vertices of the triangle. Let the vertices be A(\(x_A, y_A\)), B(\(x_B, y_B\)), and C(\(x_C, y_C\)).
- Use the distance formula to find the lengths of the sides. The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Calculate the lengths of the sides:
- Length of side AB:
\[
AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}
\] - Length of side BC:
\[
BC = \sqrt{(x_C - x_B)^2 + (y_C - y_B)^2}
\] - Length of side CA:
\[
CA = \sqrt{(x_C - x_A)^2 + (y_C - y_A)^2}
\]
- Length of side AB:
- Sum the lengths of the sides to find the perimeter of the triangle:
\[
\text{Perimeter} = AB + BC + CA
\]
Let's look at an example:
Given a triangle with vertices at A(1, 2), B(4, 6), and C(5, 1):
- Calculate the length of AB:
\[
AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Calculate the length of BC:
\[
BC = \sqrt{(5 - 4)^2 + (1 - 6)^2} = \sqrt{1^2 + (-5)^2} = \sqrt{1 + 25} = \sqrt{26} \approx 5.1
\] - Calculate the length of CA:
\[
CA = \sqrt{(5 - 1)^2 + (1 - 2)^2} = \sqrt{4^2 + (-1)^2} = \sqrt{16 + 1} = \sqrt{17} \approx 4.1
\] - Sum the lengths to find the perimeter:
\[
\text{Perimeter} = 5 + 5.1 + 4.1 = 14.2
\]
Distance Formula
The distance formula is used to find the distance between two points in a coordinate plane. This formula is derived from the Pythagorean theorem and is essential in calculating the perimeter of a triangle when the vertices are given as coordinates.
If the coordinates of two points \(A(x_1, y_1)\) and \(B(x_2, y_2)\) are known, the distance \(d\) between these points can be calculated using the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
To find the perimeter of a triangle using the distance formula, follow these steps:
- Identify the coordinates of the three vertices of the triangle. Let's denote them as \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\).
- Calculate the distance between each pair of vertices using the distance formula:
- Distance \(AB\): \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Distance \(BC\): \[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- Distance \(CA\): \[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- Add the distances calculated in the previous step to find the perimeter of the triangle:
\[ \text{Perimeter} = AB + BC + CA \]
Let's go through an example to illustrate this process:
Example: Find the perimeter of a triangle with vertices at \(A(2, 3)\), \(B(5, 7)\), and \(C(8, 3)\).
- Calculate the distance between \(A\) and \(B\):
\[ AB = \sqrt{(5 - 2)^2 + (7 - 3)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] - Calculate the distance between \(B\) and \(C\):
\[ BC = \sqrt{(8 - 5)^2 + (3 - 7)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] - Calculate the distance between \(C\) and \(A\):
\[ CA = \sqrt{(8 - 2)^2 + (3 - 3)^2} = \sqrt{6^2 + 0^2} = \sqrt{36} = 6 \] - Add the distances to find the perimeter:
\[ \text{Perimeter} = AB + BC + CA = 5 + 5 + 6 = 16 \]
Therefore, the perimeter of the triangle is 16 units.
Application in Coordinate Geometry
Coordinate geometry allows us to find the perimeter of geometric shapes plotted on the coordinate plane. This method is especially useful when the vertices of the triangle are given in coordinate form.
To find the perimeter of a triangle using coordinate geometry, follow these steps:
-
Identify the coordinates of the vertices of the triangle. For example, let's consider a triangle with vertices at \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).
-
Use the distance formula to calculate the length of each side of the triangle. The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
-
Calculate the length of side \( AB \):
\[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
-
Calculate the length of side \( BC \):
\[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
-
Calculate the length of side \( CA \):
\[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
-
-
Add the lengths of all three sides to find the perimeter of the triangle:
\[ P = AB + BC + CA \]
Let's work through a specific example:
Consider a triangle with vertices at \( A(1, 2) \), \( B(4, 6) \), and \( C(7, 2) \).
-
Calculate the length of \( AB \):
\[ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
-
Calculate the length of \( BC \):
\[ BC = \sqrt{(7 - 4)^2 + (2 - 6)^2} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
-
Calculate the length of \( CA \):
\[ CA = \sqrt{(7 - 1)^2 + (2 - 2)^2} = \sqrt{6^2 + 0} = \sqrt{36} = 6 \]
-
Add the lengths to find the perimeter:
\[ P = 5 + 5 + 6 = 16 \]
Therefore, the perimeter of the triangle with vertices at \( A(1, 2) \), \( B(4, 6) \), and \( C(7, 2) \) is 16 units.
Perimeter in Real-World Problems
The concept of perimeter is widely used in various real-world scenarios. Understanding how to calculate the perimeter of a triangle is essential for solving practical problems. Here are a few examples and step-by-step explanations of how the perimeter is applied in different contexts:
1. Fencing a Triangular Garden
Suppose you have a triangular garden with sides of lengths 15 meters, 20 meters, and 25 meters. You want to fence the garden. To determine the amount of fencing material needed, you need to calculate the perimeter of the triangle.
Step-by-Step Calculation:
- Identify the lengths of the sides: a = 15 m, b = 20 m, c = 25 m.
- Use the perimeter formula for a triangle:
P = a + b + c - Substitute the values into the formula:
P = 15 + 20 + 25 - Calculate the sum:
P = 60 meters
You need 60 meters of fencing material to enclose the garden.
2. Triangular Land Plot
Consider a triangular plot of land with vertices at coordinates (2, 3), (5, 11), and (12, 8). To find the perimeter of the land plot, you need to calculate the distances between each pair of points and then sum them.
Step-by-Step Calculation:
- Use the distance formula to find the length of each side:
d = √[(x₂ - x₁)² + (y₂ - y₁)²] - Calculate each side:
- AB = √[(5 - 2)² + (11 - 3)²] = √[9 + 64] = √73 ≈ 8.54
- BC = √[(12 - 5)² + (8 - 11)²] = √[49 + 9] = √58 ≈ 7.62
- CA = √[(12 - 2)² + (8 - 3)²] = √[100 + 25] = √125 ≈ 11.18
- Sum the lengths of the sides to find the perimeter:
P = 8.54 + 7.62 + 11.18 ≈ 27.34 units
3. Construction and Architecture
In construction and architecture, calculating the perimeter of triangular sections is crucial. For instance, when designing a triangular skylight, you need to determine the length of the frame material required.
Example: If the sides of the triangular skylight are 3 meters, 4 meters, and 5 meters:
Step-by-Step Calculation:
- Identify the side lengths: a = 3 m, b = 4 m, c = 5 m.
- Apply the perimeter formula:
P = a + b + c - Compute the perimeter:
P = 3 + 4 + 5 = 12 meters
The frame material needed for the skylight is 12 meters long.
4. Sports Fields
For triangular sports fields, such as certain sections of a baseball field or a cricket pitch, calculating the perimeter helps in determining the length of boundary lines or the amount of materials required for markings.
Example: A triangular section with sides of 50 meters, 40 meters, and 30 meters:
Step-by-Step Calculation:
- Determine the side lengths: a = 50 m, b = 40 m, c = 30 m.
- Use the perimeter formula:
P = a + b + c - Calculate the perimeter:
P = 50 + 40 + 30 = 120 meters
Thus, 120 meters of boundary material is needed for the field.
These examples demonstrate the practical use of perimeter calculations in various real-world contexts, emphasizing its importance in everyday problem-solving.
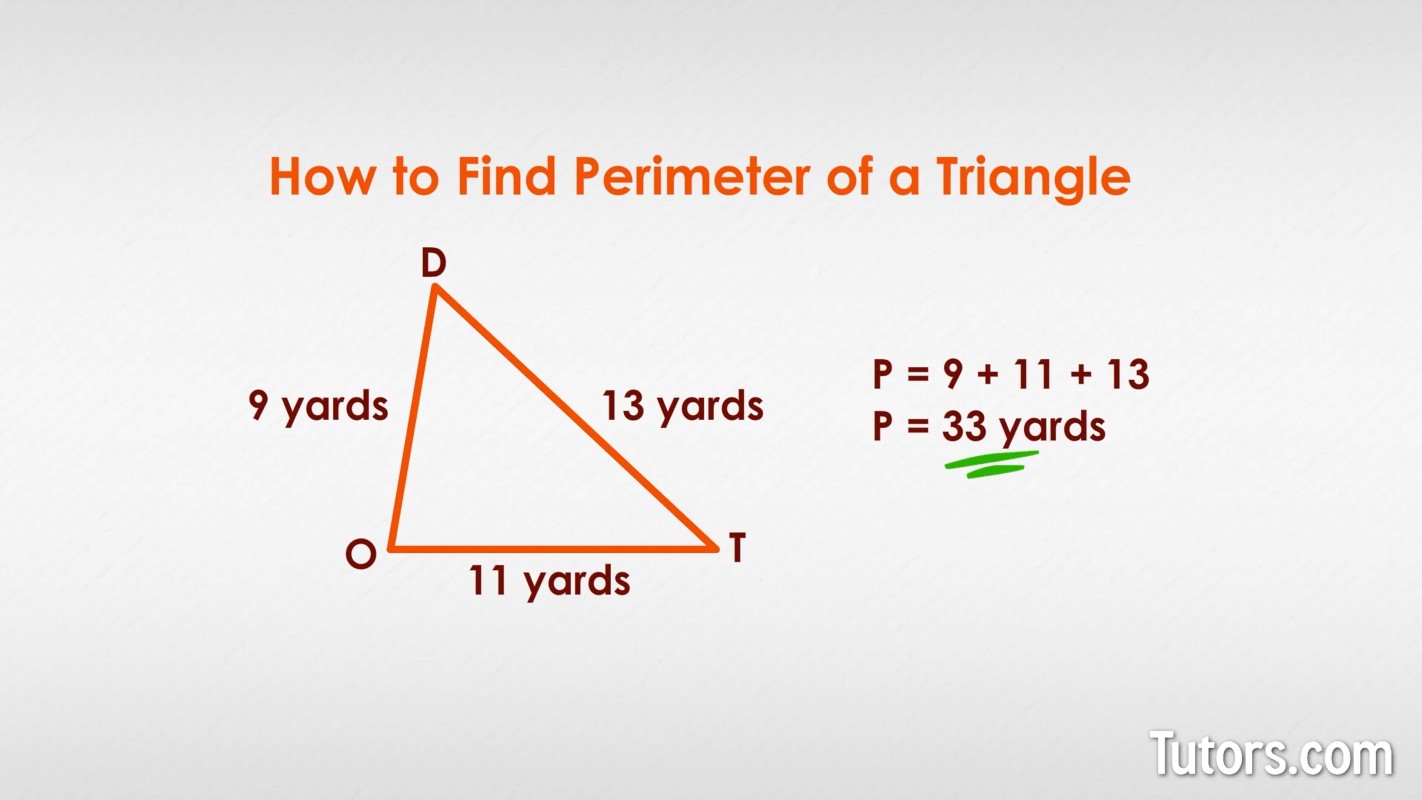
Practical Applications
The concept of finding the perimeter of a triangle is essential in various real-world applications. Here are some practical uses:
-
Construction and Architecture:
In construction, understanding the perimeter of triangular plots is crucial for planning and allocating resources. For example, when designing triangular sections of a building or garden, knowing the perimeter helps in determining the amount of materials needed for fencing or bordering.
-
Landscaping:
Landscape architects often use the perimeter of triangular areas to design gardens, parks, and outdoor spaces. Calculating the perimeter ensures accurate placement of boundaries, paths, and decorative elements.
-
Surveying and Mapping:
Surveyors use perimeter calculations to map out land parcels, especially in areas with irregular shapes. Triangular sections are common in these surveys, and knowing their perimeters is vital for accurate land division and documentation.
-
Sports Fields:
In designing sports fields and courts, such as tennis courts and running tracks, understanding the perimeter helps in creating precise layouts. For instance, the perimeter of a triangular section of a track can determine the distance athletes need to cover.
-
Interior Design:
Interior designers use perimeter measurements to plan the placement of furniture and decor within triangular spaces. Accurate measurements ensure efficient use of space and balance in room design.
-
Manufacturing:
In manufacturing, especially in the creation of metal or fabric components, calculating the perimeter of triangular parts is necessary for cutting materials to the correct size and minimizing waste.
-
Education:
Teachers use perimeter problems to help students understand geometric concepts and their real-world applications. Activities like creating mosaics or designing simple structures with known perimeters can enhance learning and engagement.
By understanding and applying the concept of the perimeter of a triangle, professionals in various fields can ensure precision and efficiency in their work, leading to better outcomes and resource management.
Common Mistakes to Avoid
When calculating the perimeter of a triangle, there are several common mistakes that students often make. Being aware of these can help ensure accurate results:
- Incorrectly Adding Side Lengths: The order in which the side lengths are added does not matter due to the commutative property of addition. However, make sure all sides are added only once.
- Mixing Units: Ensure all side lengths are in the same unit before adding them. Convert any differing units to a common unit to avoid errors.
- Confusing Perimeter with Area: Remember, perimeter is the measurement around the triangle (one-dimensional), while area measures the space within the triangle (two-dimensional).
- Missing or Misidentifying Side Lengths: Double-check that all sides are correctly identified and measured. This is particularly important in word problems and when working with diagrams.
- Using the Wrong Formula: Be sure to use the perimeter formula \( P = a + b + c \) for all types of triangles and not confuse it with other formulas, such as those for the area.
- Rounding Errors: Be cautious with rounding, especially in intermediate steps. It’s best to round only in the final answer to maintain accuracy.
By keeping these common mistakes in mind, you can improve your accuracy and ensure correct calculations of the triangle's perimeter.
Hướng dẫn tìm chu vi tam giác với video 'Cách Tìm Chu Vi Tam Giác'. Thích hợp cho bài viết về tìm chu vi tam giác.
Cách Tìm Chu Vi Tam Giác
READ MORE:
Hướng dẫn tìm chu vi tam giác với video 'Cách Tìm Chu Vi Tam Giác | Toán học cùng Mr. J'. Thích hợp cho bài viết về tìm chu vi tam giác.
Cách Tìm Chu Vi Tam Giác | Toán học cùng Mr. J