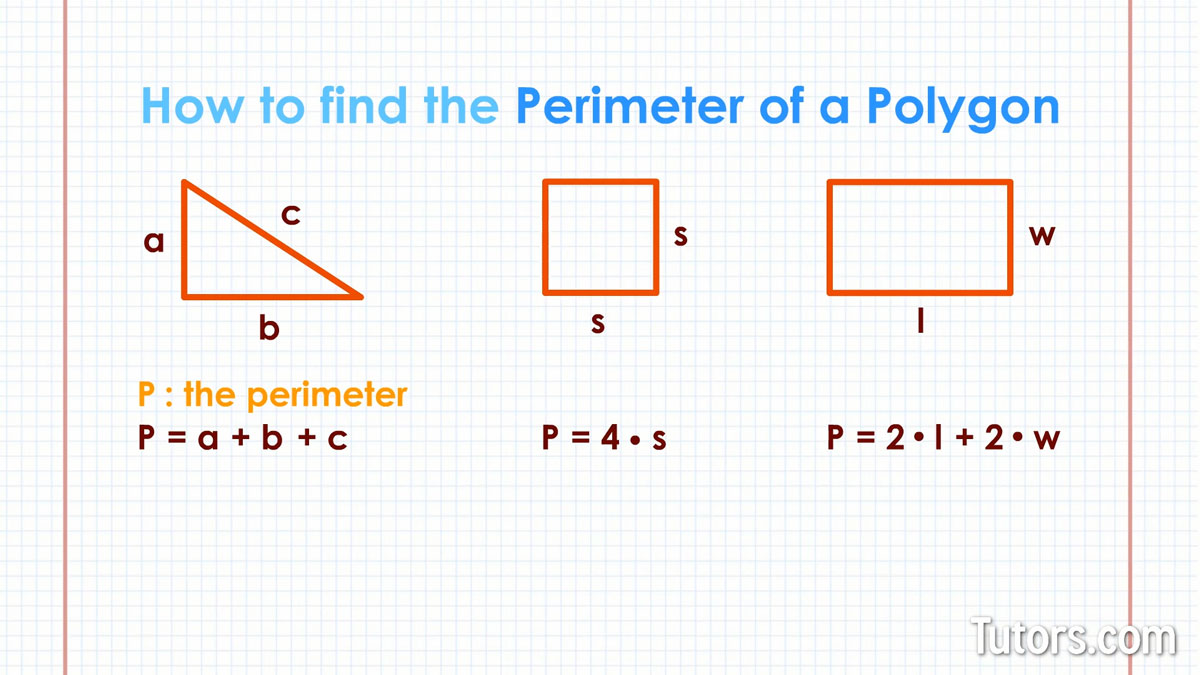
Topic formula to find perimeter of a triangle: Understanding the formula to find the perimeter of a triangle is essential for students and professionals alike. This comprehensive guide covers various methods, including formulas for different types of triangles, step-by-step examples, and practical applications. Enhance your geometry skills and apply these techniques in real-world scenarios with ease.
Table of Content
- Formula to Find Perimeter of a Triangle
- Introduction
- Basic Formula for Perimeter
- Equilateral Triangle Perimeter
- Isosceles Triangle Perimeter
- Scalene Triangle Perimeter
- Right Triangle Perimeter
- Heron's Formula for Perimeter
- Perimeter Using Coordinate Geometry
- Perimeter in Terms of Area
- Examples and Practice Problems
- Common Mistakes to Avoid
- Applications in Real Life
- Advanced Topics and Further Reading
- Conclusion
- YOUTUBE: Khám phá cách tìm chu vi của tam giác một cách dễ dàng và chính xác với video hướng dẫn của Thầy J. Video này sẽ giúp bạn nắm vững công thức và áp dụng vào các bài toán thực tế.
Formula to Find Perimeter of a Triangle
The perimeter of a triangle is the total length of all its sides. There are different formulas to calculate the perimeter depending on the type of triangle and the given information. Below are some common methods:
1. Perimeter of a Triangle with Given Side Lengths
If the lengths of all three sides of a triangle are known, the perimeter can be calculated using the formula:
\[
P = a + b + c
\]
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
2. Perimeter of an Equilateral Triangle
In an equilateral triangle, all three sides are of equal length. The perimeter can be found using the formula:
\[
P = 3a
\]
where \( a \) is the length of each side.
3. Perimeter of a Right Triangle
For a right triangle, the perimeter can be calculated if the lengths of the two legs (\( a \) and \( b \)) and the hypotenuse (\( c \)) are known:
\[
P = a + b + c
\]
Alternatively, if only the legs are known, the hypotenuse can be found using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
4. Perimeter Using Coordinates (Distance Formula)
If the vertices of a triangle are known in the coordinate plane as \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\), the perimeter can be found by calculating the distances between each pair of points and then summing them:
\[
d_1 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
\[
d_2 = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2}
\]
\[
d_3 = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2}
\]
Then, the perimeter \( P \) is given by:
\[
P = d_1 + d_2 + d_3
\]
Example Calculation
Consider a triangle with sides of lengths 3, 4, and 5 units. The perimeter is:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]

READ MORE:
Introduction
The perimeter of a triangle is a fundamental concept in geometry, representing the total distance around the triangle. Calculating the perimeter is straightforward once you understand the different methods and formulas available. This guide will walk you through the various ways to find the perimeter of different types of triangles, from the simplest to more advanced techniques.
Triangles are classified into several types based on their sides and angles, and the method to find the perimeter can vary accordingly. Here’s a detailed overview of how to calculate the perimeter for each type:
- Equilateral Triangle: All three sides are equal.
- Isosceles Triangle: Two sides are of equal length.
- Scalene Triangle: All three sides are of different lengths.
- Right Triangle: One angle is a right angle (90 degrees).
In this article, we will cover the following topics step by step:
- Basic Formula for Perimeter - Using the sum of all sides.
- Special Formulas for Specific Types of Triangles - Including equilateral, isosceles, and right triangles.
- Heron's Formula - A method to find the perimeter when only the side lengths are known.
- Using Coordinate Geometry - Calculating perimeter when the vertices of the triangle are given in a coordinate plane.
- Practical Examples and Applications - Real-world scenarios where calculating the perimeter is essential.
By the end of this guide, you will have a thorough understanding of how to find the perimeter of any triangle, making it easy to apply this knowledge in both academic and practical contexts.
Basic Formula for Perimeter
The perimeter of a triangle is the total distance around the boundary of the triangle. To calculate the perimeter, you simply add the lengths of all three sides of the triangle. The formula is straightforward:
Using MathJax, the formula for the perimeter \( P \) of a triangle with sides \( a \), \( b \), and \( c \) can be expressed as:
\[ P = a + b + c \]
Here's a step-by-step process to find the perimeter:
- Measure the lengths of all three sides of the triangle.
- Ensure all side lengths are in the same unit (e.g., all in centimeters or all in inches).
- Add the lengths of the three sides together using the formula.
- State the perimeter with the appropriate unit of measurement.
For different types of triangles, the basic formula still applies:
- Equilateral Triangle: All three sides are equal. The perimeter is \( 3a \), where \( a \) is the length of one side.
- Isosceles Triangle: Two sides are equal. The perimeter is \( 2a + b \), where \( a \) is the length of the equal sides and \( b \) is the length of the base.
- Scalene Triangle: All three sides are different. The perimeter is \( a + b + c \).
- Right Triangle: The sides include the base (\( b \)), the perpendicular (\( p \)), and the hypotenuse (\( h \)). The perimeter is \( b + p + h \). If the hypotenuse is not known, use the Pythagorean theorem \( h = \sqrt{b^2 + p^2} \).
| Triangle Type | Formula |
| Equilateral | \( P = 3a \) |
| Isosceles | \( P = 2a + b \) |
| Scalene | \( P = a + b + c \) |
| Right | \( P = b + p + h \) or \( P = b + p + \sqrt{b^2 + p^2} \) |
Equilateral Triangle Perimeter
An equilateral triangle is a triangle in which all three sides are equal in length and all three angles are equal, each measuring 60 degrees. The formula to find the perimeter of an equilateral triangle is straightforward due to its symmetrical properties. Here is a detailed explanation of how to calculate it:
- Identify the length of one side of the equilateral triangle, denoted as a.
- Since all sides are equal, multiply the length of one side by 3 to get the perimeter.
The formula for the perimeter P of an equilateral triangle with side length a is given by:
\( P = 3a \)
Let's go through a few examples to better understand the application of this formula:
- Example 1: If each side of the equilateral triangle is 5 cm, then the perimeter is \( P = 3 \times 5 = 15 \) cm.
- Example 2: For a triangle with a side length of 7.9 cm, the perimeter will be \( P = 3 \times 7.9 = 23.7 \) cm.
- Example 3: If the side length is given as 12 units, then the perimeter will be \( P = 3 \times 12 = 36 \) units.
This simple multiplication rule makes it easy to calculate the perimeter of an equilateral triangle quickly and accurately. Whether used in geometry problems, construction, or design, knowing how to find the perimeter is a fundamental skill.
Isosceles Triangle Perimeter
An isosceles triangle is a triangle with two sides of equal length. The formula to calculate the perimeter of an isosceles triangle is straightforward and involves the lengths of the equal sides and the base of the triangle. The basic formula is:
\[
P = 2a + b
\]
where \( a \) is the length of each of the two equal sides, and \( b \) is the length of the base.
Here are the steps to calculate the perimeter of an isosceles triangle:
- Identify the lengths of the two equal sides (a) and the base (b) of the triangle.
- Substitute these values into the formula \( P = 2a + b \).
- Perform the arithmetic to find the perimeter.
For example, if the two equal sides are each 5 units long and the base is 6 units long, the perimeter would be calculated as follows:
\[
P = 2 \times 5 + 6 = 10 + 6 = 16 \, \text{units}
\]
Let's consider a few specific cases:
- Isosceles Right Triangle: If an isosceles triangle is also a right triangle, it will have two equal legs and a hypotenuse. For such triangles, the legs are equal, and the hypotenuse can be found using the Pythagorean theorem. For example, if the hypotenuse is 6 units: \[ a = \sqrt{\left(\frac{6}{\sqrt{2}}\right)^2} = 3\sqrt{2} \] The perimeter would be: \[ P = 2 \times 3\sqrt{2} + 6 = 6\sqrt{2} + 6 \]
- General Isosceles Triangle: If the sides are 8 units and the base is 7 units: \[ P = 2 \times 8 + 7 = 16 + 7 = 23 \, \text{units} \]
Using these formulas, one can easily find the perimeter of any isosceles triangle given the lengths of its sides.
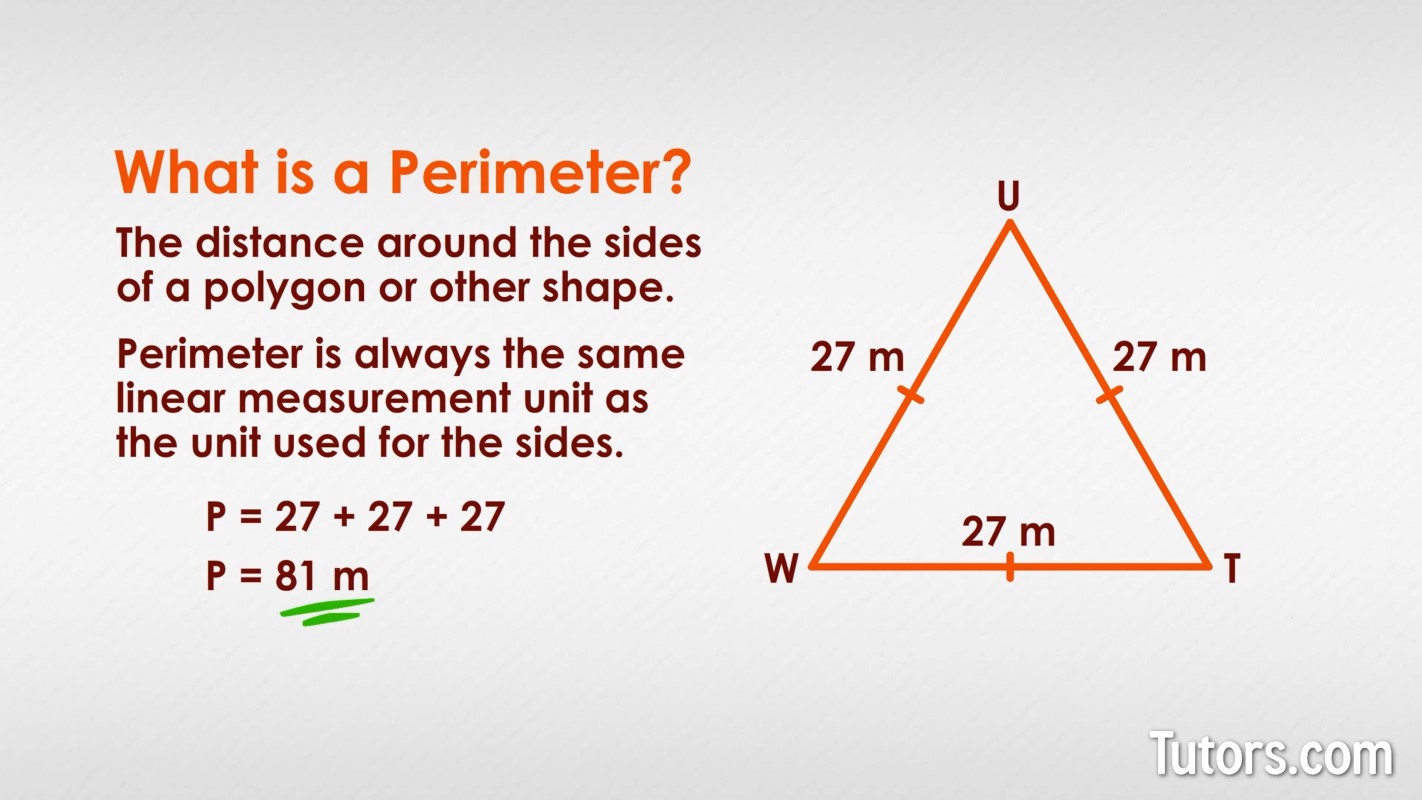
Scalene Triangle Perimeter
A scalene triangle is a triangle where all three sides have different lengths, and therefore, all three angles are different as well. The perimeter of a scalene triangle can be found by simply summing the lengths of its three sides. Here's a step-by-step guide to finding the perimeter of a scalene triangle:
- Identify the lengths of all three sides of the triangle. Let these lengths be denoted as \(a\), \(b\), and \(c\).
- Use the perimeter formula for a scalene triangle, which is: \[ \text{Perimeter} = a + b + c \]
- Substitute the known side lengths into the formula and perform the addition.
For example, if the sides of a scalene triangle are 5 cm, 7 cm, and 9 cm, the perimeter would be calculated as follows:
- Given: \(a = 5 \, \text{cm}\), \(b = 7 \, \text{cm}\), \(c = 9 \, \text{cm}\)
- Calculate the perimeter: \[ \text{Perimeter} = 5 + 7 + 9 = 21 \, \text{cm} \]
Therefore, the perimeter of the triangle is 21 cm.
| Side Lengths | Perimeter Calculation |
| 5 cm, 7 cm, 9 cm | 5 + 7 + 9 = 21 cm |
| 3 cm, 4 cm, 6 cm | 3 + 4 + 6 = 13 cm |
| 2 cm, 8 cm, 10 cm | 2 + 8 + 10 = 20 cm |
This straightforward method works for any scalene triangle as long as the lengths of all three sides are known.
Right Triangle Perimeter
The perimeter of a right triangle is the sum of all its three sides. In a right triangle, the sides include the base (a), the height (b), and the hypotenuse (c). The formula to calculate the perimeter of a right triangle is:
\[ \text{Perimeter} = a + b + c \]
Here's how you can determine the perimeter step by step:
- Identify the lengths of the two legs (a and b).
- Use the Pythagorean theorem to find the length of the hypotenuse if it is not provided: \[ c = \sqrt{a^2 + b^2} \]
- Add the lengths of all three sides to find the perimeter: \[ \text{Perimeter} = a + b + c \]
Let's consider an example:
| Side a | 5 m |
| Side b | 12 m |
| Hypotenuse (c) | \[ c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \, \text{m} \] |
| Perimeter | \[ 5 + 12 + 13 = 30 \, \text{m} \] |
The perimeter of a right triangle with sides 5 m, 12 m, and 13 m is 30 meters.
Heron's Formula for Perimeter
Heron's formula allows us to find the area of a triangle when we know the lengths of all three sides. It's a valuable tool for solving problems without needing to know the height of the triangle.
The formula is named after Hero (or Heron) of Alexandria and has been known for nearly 2000 years. Here is the step-by-step process to use Heron's formula:
- Calculate the semi-perimeter of the triangle. The semi-perimeter, denoted as s, is half of the triangle's perimeter:
\[ s = \frac{a + b + c}{2} \]
- Apply Heron's formula to find the area of the triangle. Heron's formula states:
\[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
Example Calculation
Consider a triangle with side lengths 5, 6, and 7 units. Follow these steps to find the area:
- Calculate the semi-perimeter:
\[ s = \frac{5 + 6 + 7}{2} = 9 \]
- Apply Heron's formula:
\[ A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} \]
\[ A = \sqrt{9 \times 4 \times 3 \times 2} \]
\[ A = \sqrt{216} \]
\[ A \approx 14.7 \text{ square units} \]
Advantages of Heron's Formula
- Useful for any type of triangle (equilateral, isosceles, scalene).
- Does not require knowledge of the height or angles of the triangle.
- Can be extended to find the area of quadrilaterals by dividing them into two triangles.
Perimeter Using Coordinate Geometry
To find the perimeter of a triangle in coordinate geometry, you need to determine the lengths of its sides using the coordinates of its vertices. Here is a step-by-step guide on how to do this:
- Identify the coordinates of the three vertices of the triangle. Let the vertices be \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \).
- Use the distance formula to calculate the lengths of the sides. The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Calculate the length of each side:
- For side \( AB \):
\[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- For side \( BC \):
\[ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- For side \( CA \):
\[ CA = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} \]
- For side \( AB \):
- Add the lengths of the three sides to find the perimeter:
\[ \text{Perimeter} = AB + BC + CA \]
Example Calculation
Let's find the perimeter of a triangle with vertices at \( A(1, 2) \), \( B(4, 6) \), and \( C(5, 3) \).
- Calculate \( AB \):
\[ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]
- Calculate \( BC \):
\[ BC = \sqrt{(5 - 4)^2 + (3 - 6)^2} = \sqrt{1^2 + (-3)^2} = \sqrt{1 + 9} = \sqrt{10} \approx 3.16 \text{ units} \]
- Calculate \( CA \):
\[ CA = \sqrt{(5 - 1)^2 + (3 - 2)^2} = \sqrt{4^2 + 1^2} = \sqrt{16 + 1} = \sqrt{17} \approx 4.12 \text{ units} \]
- Add the lengths to find the perimeter:
\[ \text{Perimeter} = 5 + 3.16 + 4.12 \approx 12.28 \text{ units} \]
Advantages of Using Coordinate Geometry
- Accurate measurement of side lengths using coordinates.
- Applicable to any type of triangle, regardless of the orientation on the plane.
- Facilitates integration with other geometric concepts and theorems.

Perimeter in Terms of Area
Understanding the relationship between the perimeter and the area of a triangle can be quite insightful. While the two properties measure different aspects of a triangle, there are specific formulas that connect them. Here are the detailed steps and formulas to find the perimeter of a triangle in terms of its area:
1. Using Heron's Formula:
Heron's formula is a way to find the area of a triangle when you know the lengths of all three sides. Let's denote the sides of the triangle as \(a\), \(b\), and \(c\).
First, calculate the semi-perimeter \(s\) of the triangle:
\[
s = \frac{a + b + c}{2}
\]
Then, the area \(A\) of the triangle can be found using:
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
If we know the area \(A\) and the sides \(a\), \(b\), and \(c\), we can rearrange the formula to express the perimeter in terms of the area.
2. Relationship in Special Triangles:
- Equilateral Triangle:
For an equilateral triangle with side length \(a\), the perimeter \(P\) and area \(A\) are related as follows:
\[
A = \frac{\sqrt{3}}{4} a^2
\]The perimeter \(P\) is then:
\[
P = 3a
\]So, expressing \(a\) in terms of \(A\) and substituting, we get:
\[
a = \sqrt{\frac{4A}{\sqrt{3}}}
\]Therefore, the perimeter in terms of the area is:
\[
P = 3 \sqrt{\frac{4A}{\sqrt{3}}}
\] - Right Triangle:
For a right triangle, the area \(A\) is given by:
\[
A = \frac{1}{2} \times base \times height
\]Given the Pythagorean theorem \(c^2 = a^2 + b^2\) (where \(c\) is the hypotenuse), the perimeter \(P\) can be expressed as:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
3. General Formula for Any Triangle:
For any triangle, knowing the area \(A\) and sides \(a\), \(b\), and \(c\), we can find the semi-perimeter \(s\) using the formula:
\[
s = \frac{a + b + c}{2}
\]
The perimeter \(P\) is then simply:
\[
P = 2s
\]
Using these approaches, you can relate the perimeter of a triangle to its area, depending on the type of triangle and the known values.
Examples and Practice Problems
Understanding the perimeter of a triangle is crucial in geometry. Below are some examples and practice problems to help you master this concept.
Example 1: Finding the Perimeter of a Right Triangle
Given a right triangle with sides PQ = 4 inches and QR = 3 inches, find the perimeter.
- First, calculate the length of the hypotenuse (PR) using the Pythagorean theorem: \[ PR^2 = PQ^2 + QR^2 \] \[ PR^2 = 4^2 + 3^2 = 16 + 9 = 25 \] \[ PR = \sqrt{25} = 5 \text{ inches} \]
- Now, add all the sides to find the perimeter: \[ P = PQ + QR + PR = 4 + 3 + 5 = 12 \text{ inches} \]
Example 2: Equilateral Triangle
Find the perimeter of an equilateral triangle where each side is 10 cm.
- Since all sides are equal, the formula is: \[ P = 3a \]
- Substitute the length of the side: \[ P = 3 \times 10 = 30 \text{ cm} \]
Example 3: Isosceles Triangle
Find the missing side of an isosceles triangle with a perimeter of 40 cm and two sides each of 10 cm.
- Let the missing side be \( b \). Given: \[ P = 2a + b \] \[ 40 = 2 \times 10 + b \]
- Solve for \( b \): \[ 40 = 20 + b \implies b = 20 \text{ cm} \]
Practice Problems
- Find the perimeter of a triangle with sides 7 cm, 24 cm, and 25 cm.
- A triangle has a perimeter of 30 inches. Two sides are 8 inches and 12 inches. Find the third side.
- Calculate the perimeter of an equilateral triangle where each side measures 15 m.
- A right triangle has one leg measuring 9 units and the other leg measuring 12 units. Find its perimeter.
These examples and practice problems should help you become more comfortable with finding the perimeter of various types of triangles. Remember, practice is key to mastering these concepts!
Common Mistakes to Avoid
When calculating the perimeter of a triangle, there are several common mistakes that students often make. Avoiding these errors can help ensure accurate results:
- Incorrect Formula Usage: Always use the correct formula for the type of triangle you are dealing with. For example, for a scalene triangle, use \( P = a + b + c \), where \( a \), \( b \), and \( c \) are the lengths of the sides. For an equilateral triangle, use \( P = 3a \), where \( a \) is the length of a side.
- Misidentifying Triangle Types: Ensure you correctly identify whether the triangle is equilateral, isosceles, scalene, or right-angled, as this affects which formula to use.
- Calculation Errors: Double-check your arithmetic when adding the side lengths. Simple addition errors can lead to incorrect results.
- Forgetting Units: Always include the units of measurement in your final answer. If the side lengths are in centimeters, then the perimeter should also be expressed in centimeters.
- Incorrect Side Lengths: Ensure you are using the correct side lengths for your calculations. In right triangles, use the Pythagorean theorem to find the correct lengths if only two sides are known.
- Ignoring Special Conditions: Be aware of specific conditions such as using the distance formula for triangles plotted on a coordinate plane or using Heron's formula when the sides but not the angles are known.
- Neglecting Simplifications: Simplify expressions where possible. For example, in an equilateral triangle, rather than adding the same side length three times, multiply the side length by three.
Applications in Real Life
The perimeter of a triangle, like other geometric measurements, has numerous practical applications in everyday life. Here are some key areas where the concept is utilized:
- Construction and Architecture: When designing buildings, accurate perimeter measurements are crucial for determining the lengths of materials needed for walls, doors, and windows. For example, calculating the perimeter of triangular sections in roofs helps in planning the amount of roofing material required.
- Landscaping and Gardening: In landscape design, the perimeter of triangular flower beds or plots needs to be measured to determine the amount of fencing or edging required. This ensures that materials are purchased efficiently without excess or shortage.
- Interior Design: When laying out rooms and spaces, the perimeter measurements help in planning the placement of furniture, fixtures, and decorations. For instance, calculating the perimeter of a triangular dining area can help in deciding the amount of skirting or baseboard needed.
- Sports and Recreational Areas: Perimeter calculations are essential in designing sports fields and playgrounds. For example, determining the perimeter of a triangular section of a track field helps in marking boundaries accurately.
- Fabrication and Manufacturing: In industries such as fabric and clothing manufacturing, perimeter measurements are used to cut materials precisely. For instance, designing a triangular piece of fabric requires knowing its perimeter to ensure accurate cuts and minimal waste.
- Art and Design: Artists and designers use perimeter calculations to create frames, borders, and other structural elements in their work. For example, framing a triangular painting involves measuring the perimeter to ensure the frame fits perfectly.
- Navigation and Surveying: In fields like surveying and navigation, the perimeter of land plots and geographical areas is measured for mapping and property delineation. This is crucial for legal documentation and land management.
Understanding the perimeter of a triangle and other shapes not only aids in these practical applications but also enhances problem-solving skills and logical reasoning, which are valuable in various professional fields.

Advanced Topics and Further Reading
The study of the perimeter of a triangle extends beyond simple formulas and basic calculations. Here are some advanced topics and further reading materials that delve deeper into the geometric and mathematical properties of triangles:
1. Perimeter in Non-Euclidean Geometry
Non-Euclidean geometry explores spaces where the traditional rules of Euclidean geometry do not apply. For instance, in spherical geometry, the sum of the angles of a triangle exceeds 180 degrees, affecting the calculation of the perimeter. This topic explores the implications and adjustments needed for perimeter calculations in such geometries.
2. Perimeter and Optimization Problems
Optimization problems often involve finding the maximum or minimum perimeter for a given area or other constraints. This is particularly relevant in fields such as operations research, economics, and engineering. Studying these problems provides insight into how perimeter calculations can be applied to real-world scenarios to optimize resources and designs.
3. Computational Geometry and Algorithm Design
In computational geometry, algorithms are designed to efficiently calculate the perimeter of complex shapes, including polygons and polyhedra. This area of study is crucial in computer graphics, geographic information systems (GIS), and robotics, where accurate and efficient perimeter calculations are necessary.
4. Advanced Trigonometric Applications
Trigonometry plays a significant role in advanced perimeter calculations, especially when dealing with oblique triangles. The law of sines and cosines are used to find missing sides and angles, which in turn help in calculating the perimeter. These principles are essential in various scientific and engineering applications.
5. Perimeter in Analytic Geometry
Analytic geometry, or coordinate geometry, involves using algebraic equations to represent geometric shapes. Calculating the perimeter of a triangle with vertices given in coordinates involves distance formulas and vector analysis. This topic is fundamental in understanding how algebra and geometry intersect.
6. Perimeter and Topology
Topology studies properties of space that are preserved under continuous deformations. It examines how the concept of perimeter changes when the shape of a triangle is stretched or bent without tearing. This area of study is abstract but has profound implications in modern mathematics and theoretical physics.
Further Reading
Exploring these advanced topics and further readings will provide a deeper understanding of the perimeter of a triangle and its applications in various fields of mathematics and beyond.
Conclusion
The perimeter of a triangle is a fundamental concept in geometry, essential for both academic and practical applications. Whether dealing with simple equilateral triangles or complex scalene triangles, the formula for calculating the perimeter remains straightforward: add the lengths of all three sides.
Understanding the perimeter allows for various real-life applications such as determining the amount of materials needed for construction, fencing a garden, or designing objects. The formula is versatile and can be adapted using trigonometric principles like the Law of Sines and Cosines when only partial information is available.
To summarize, mastering the perimeter calculation of a triangle involves:
- Using the basic formula \( P = a + b + c \) for any triangle.
- Applying the Law of Cosines and Law of Sines for non-right triangles with known sides and angles.
- Employing coordinate geometry for triangles with known vertex coordinates.
By exploring various methods and applying these concepts to real-world scenarios, one gains a deeper appreciation and practical understanding of geometry. Keep practicing with different types of triangles and explore advanced topics to further enhance your mathematical skills.
Khám phá cách tìm chu vi của tam giác một cách dễ dàng và chính xác với video hướng dẫn của Thầy J. Video này sẽ giúp bạn nắm vững công thức và áp dụng vào các bài toán thực tế.
Cách Tìm Chu Vi Tam Giác | Toán với Thầy J
READ MORE:
Khám phá cách tìm chu vi của tam giác một cách dễ dàng và chính xác. Video này sẽ giúp bạn nắm vững công thức và áp dụng vào các bài toán thực tế.
Cách Tìm Chu Vi Tam Giác