Perimeter of a Kite: Unlocking the Secrets of This Classic Quadrilateral

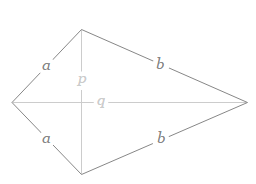
A kite, in geometrical terms, is a unique quadrilateral featuring distinct characteristics that set it apart from other four-sided shapes. It is defined by two pairs of adjacent, congruent sides. These pairs are not necessarily of equal length to each other, giving the kite its distinctive shape.

• Adjacent Congruent Sides: In a kite, each pair of adjacent sides (sides that meet) are of equal length. This aspect differentiates a kite from other quadrilaterals.
• Angles: The angles between the unequal sides are congruent, meaning the angles where the longer sides meet are equal, as are the angles where the shorter sides meet.
• Diagonals: The diagonals of a kite have unique properties. One diagonal bisects the other at a right angle (90°), which is a defining feature of kites.
• Symmetry: Kites have one axis of symmetry along the diagonal that bisects the other. This symmetry contributes to its distinct shape and properties.

Understanding these fundamental properties is crucial for exploring the perimeter of a kite, which is the total distance around its boundary. The perimeter calculation involves adding the lengths of all four sides, but due to the kite\"s properties, it can be simplified using a specific formula.

The calculation of a kite\"s perimeter is straightforward, relying on a simple formula that considers the lengths of its sides. As a kite has two pairs of equal-length sides, this formula simplifies the process significantly.

Perimeter Formula: The perimeter (P) of a kite is calculated as P = 2(a + b), where \"a\" and \"b\" represent the lengths of the two distinct pairs of adjacent sides of the kite.

1. Identify Side Lengths: Measure or obtain the lengths of one pair of adjacent sides (a) and the other pair (b).
2. Apply the Formula: Insert these values into the formula P = 2(a + b).
3. Calculate: Multiply the sum of the side lengths by 2 to get the total perimeter.

This formula leverages the kite\"s property of having two pairs of equal-length adjacent sides, streamlining the process of calculating its perimeter. It\"s a fundamental tool in geometric analysis and practical applications, like crafting or construction, where knowing the boundary length is essential.

Remember, the accuracy of the perimeter calculation is contingent on precise measurements of the kite\"s sides. Any error in these measurements can lead to an incorrect estimation of the kite\"s perimeter.

Calculating the perimeter of a kite involves a series of straightforward steps, utilizing the basic formula P = 2(a + b). Here\"s how you can accurately determine this measurement:

1. Determine Side Lengths: Identify and measure the lengths of the two distinct pairs of adjacent sides of the kite. Label one pair as \"a\" and the other as \"b\".
2. Apply the Formula: Insert these lengths into the perimeter formula P = 2(a + b).
3. Perform the Calculation: Multiply the sum of the side lengths by 2. This result gives you the total perimeter of the kite.
4. Verification: To verify the accuracy, you might draw a diagram and use geometric principles or a right triangle calculator for complex shapes, especially if the kite is not a standard one.
5. Consider Different Shapes: Remember, a kite can be convex or concave. In concave kites, one of the diagonals lies outside the kite\"s shape, which might require additional geometric consideration.
6. Special Cases: In certain cases, such as when all sides are equal (making the kite a rhombus) or when all angles are 90 degrees (making it a square), the calculation might differ slightly.

Following these steps will guide you through the calculation of a kite\"s perimeter, ensuring precision and understanding of the geometric principles involved.

Diagonals play a crucial role in defining the geometric properties of a kite. A kite has two diagonals that intersect at a right angle, forming four right angles within its shape. This perpendicular intersection is a defining characteristic of kite diagonals.

• Length and Intersection: The diagonals of a kite are not of equal length; one is longer than the other. The longer diagonal bisects the shorter one, creating two congruent right triangles within the kite.
• Angles and Bisecting: The diagonal of a kite that bisects its non-congruent angles divides them into equal parts. This diagonal typically bisects the angles at the kite\"s tips.
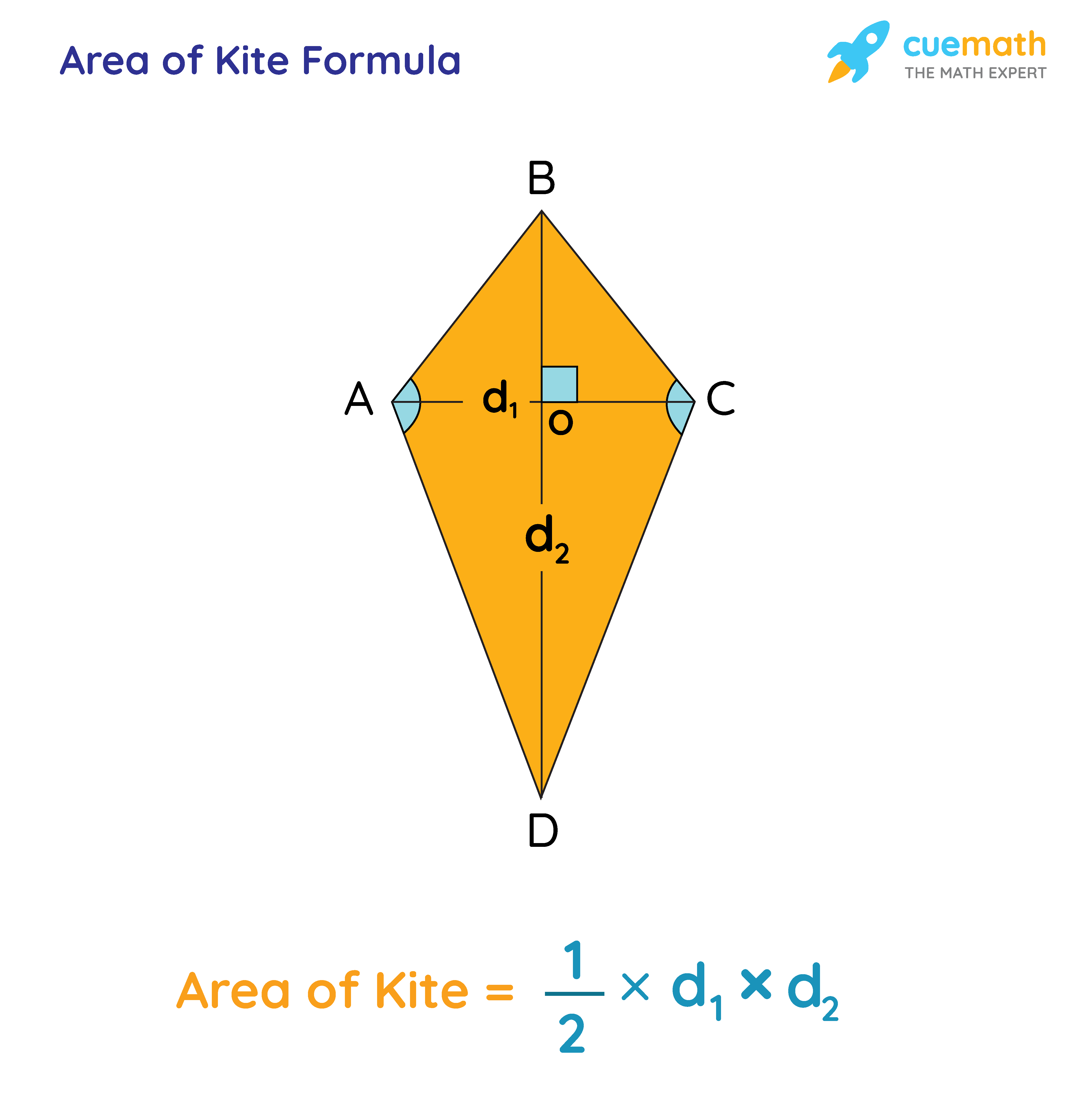
• Area Calculation: The area of a kite can be calculated using the formula: Area = 1/2 × Product of Diagonals. This formula takes advantage of the kite\"s diagonal properties, especially their perpendicular nature.
• Special Cases: In certain kites, known as right kites, two opposite angles are right angles. These kites are notable for their ability to circumscribe one circle and be inscribed in another, making them bicentric or even tricentric.

Understanding these diagonal properties provides a deeper insight into the kite\"s structure and aids in solving various geometrical problems related to kites, such as calculating areas and understanding their symmetry.

Applying the perimeter formula of a kite can be understood better through practical examples. Let\"s delve into some scenarios that demonstrate how to calculate the perimeter of a kite in different contexts.

1. Example 1:
2. A kite has sides measuring 15 cm and 20 cm. To find its perimeter, we apply the formula P = 2(a + b). Here, a = 15 cm, and b = 20 cm. Therefore, the perimeter is 2(15 + 20) = 2 × 35 = 70 cm.
3. Example 2:
4. Consider a kite where the lengths of the sides are in a ratio of 3:5. If the smaller side is 24 inches, the perimeter is calculated by first determining the length of the larger side, which in this case is 40 inches. Then, using P = 2(a + b), the perimeter equals 2(24 + 40) = 2 × 64 = 128 inches.
5. Example 3:
6. For a kite with side lengths of 12 m and 10 m, the perimeter calculation using P = 2(a + b) results in 2(12 + 10) = 2 × 22 = 44 m.
7. Example 4:
8. Imagine a kite with equal sides of 20 cm and 35 cm. The perimeter would be calculated as P = 2(20 + 35) = 2 × 55 = 110 cm.
9. Example 5:
10. For a kite with pairs of equal sides measuring 2 and 5 units respectively, the perimeter is simply the sum of all these sides, which calculates to 2+2+5+5 = 14 units.

These examples illustrate the versatility of the perimeter formula for a kite, P = 2(a + b), in various practical scenarios, helping in understanding and solving real-world problems related to kites.

Understanding the unique aspects of a kite\"s perimeter involves comparing it with other quadrilaterals like squares, rectangles, parallelograms, and rhombuses. Each of these quadrilaterals has distinct properties that differentiate their perimeters from that of a kite.

• Rhombus: Similar to a kite, a rhombus has four congruent sides. However, unlike a kite, all sides of a rhombus are equal in length and opposite sides are parallel, which is not the case with kites.
• Rectangle: A rectangle has opposite sides that are equal and parallel, which differs from a kite\"s adjacent equal sides. The perimeter of a rectangle is twice the sum of its length and width.
• Square: A square is a special type of rectangle where all four sides are equal. This differs from a kite, where only adjacent sides are equal.
• Parallelogram: A parallelogram, like a kite, has two pairs of equal-length sides. However, in parallelograms, the equal sides are opposite to each other rather than adjacent.
• Isosceles Trapezoid: An isosceles trapezoid, which has a pair of non-parallel sides that are equal in length, is another quadrilateral with some resemblance to kites in terms of symmetry but differs in side and angle properties.

These comparisons highlight that while there are similarities in terms of equal side lengths in some cases, the arrangement of these sides and the angles formed, which play a crucial role in defining the perimeter, are what distinguish a kite from other quadrilaterals.

Understanding the perimeter of a kite becomes easier and more engaging with the help of interactive tools and resources available online. These tools not only provide a hands-on learning experience but also make the learning process enjoyable and effective.

• Transum Mathematics: This platform offers a variety of exercises and puzzles related to the perimeter of kites and other mathematical concepts. It is designed to enhance understanding through practice, allowing users to apply their knowledge in practical scenarios. The site also includes a range of activities, games, and investigations that are perfect for starters or supplementary learning materials.
• Omni Calculator: The Omni Calculator for kite geometry is a user-friendly tool that simplifies the calculation of a kite\"s perimeter. It requires input of the two unequal sides of the kite, after which it applies the perimeter formula. This tool is especially useful for visualizing how changes in side lengths affect the perimeter, providing an interactive and practical approach to understanding kite geometry.
• Math Is Fun: This website offers a comprehensive overview of the properties of kites in geometry, including their perimeters. It provides clear explanations and examples, along with a playful interface to experiment with kite dimensions and observe how these changes impact the perimeter.
• Math Worksheets 4 Kids: For educators and students, this resource offers a collection of worksheets specifically designed for practicing the calculation of kite perimeters. These worksheets cater to a range of levels and include dimensions presented in various forms like integers, decimals, and fractions, making them a versatile educational tool.

These resources not only aid in the understanding of the perimeter of kites but also make the learning process more interactive and fun. By utilizing these tools, learners can strengthen their grasp on geometric concepts and apply them to solve real-world problems effectively.

• What is the formula for the perimeter of a kite?
• The perimeter of a kite is calculated using the formula 2a + 2b, where \"a\" and \"b\" represent the lengths of the two pairs of adjacent, equal sides of the kite.
• How is the perimeter of a kite calculated?
• To calculate the perimeter of a kite, measure the lengths of the two different pairs of adjacent sides and apply the formula: Perimeter = 2(a + b). For instance, if one pair of sides is each 15 cm and the other pair is each 20 cm, the perimeter would be 2(15 + 20) = 70 cm.
• Are all opposing angles of a kite equal?
• No, in a kite, only the angles between the pairs of congruent (equal length) sides are equal. The other opposing angles are not necessarily equal.
• Can a kite be considered a parallelogram?
• No, a kite is not a parallelogram. In a parallelogram, opposite sides are congruent and parallel, which is not the case for kites.
• What if all sides of a kite are congruent?
• If all sides of a kite are congruent, it becomes a rhombus, a special type of kite that follows all the properties of a rhombus.
• How to find the area of a kite?
• The area of a kite can be calculated as half the product of its diagonals. The formula is: Area = ½ × d1 × d2, where d1 and d2 are the lengths of the diagonals.

The study of kites in geometry extends beyond their basic definitions and properties. Advanced concepts delve into the intricate geometric relationships and theorems involving kites. This section explores these deeper aspects and suggests further reading for enthusiastic learners.

1. Properties of Kite Diagonals: Kite diagonals intersect at right angles, with the longer diagonal bisecting the shorter one. This leads to the formation of congruent triangles and isosceles triangles, offering a rich ground for exploring congruence and similarity principles in geometry.
2. Perimeter and Area Calculations: Advanced problems may involve using the Pythagorean Theorem to determine the lengths of sides or diagonals, which are then used to calculate the kite\"s perimeter and area. For instance, finding the area of a kite with given diagonal lengths involves half the product of the diagonals, leading to practical applications in various fields.
3. Angle Relationships: The sum of the interior angles in a kite is 360°, with one pair of non-adjacent angles (the obtuse angles) being equal. This opens up discussions on angle properties in quadrilaterals and their applications.
4. Special Quadrilaterals: Exploring the conditions under which a kite can also be classified as other types of quadrilaterals, such as cyclic quadrilaterals, and understanding their unique properties.
5. Coordinate Geometry Applications: Analyzing the properties of kites within the coordinate plane, such as determining whether a set of given points forms a kite, and calculating its area and perimeter using coordinate geometry techniques.
6. Challenging Questions: Engaging with complex problems like whether a kite with certain side lengths can exist or whether a kite can be considered a parallelogram under specific conditions.

For further reading and a more comprehensive understanding of these advanced concepts, it is recommended to explore geometry textbooks and scholarly articles that focus on quadrilaterals and their properties. Interactive learning tools and online platforms can also provide practical experience in solving complex problems involving kites.

Discover the fascinating world of kites in geometry! Our comprehensive guide on the perimeter of kites not only simplifies this concept but also opens doors to advanced geometric explorations. Join us on this intriguing journey and unravel the mysteries of kite geometry!