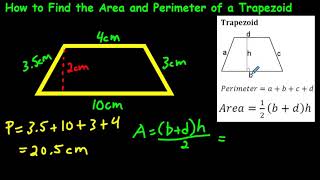
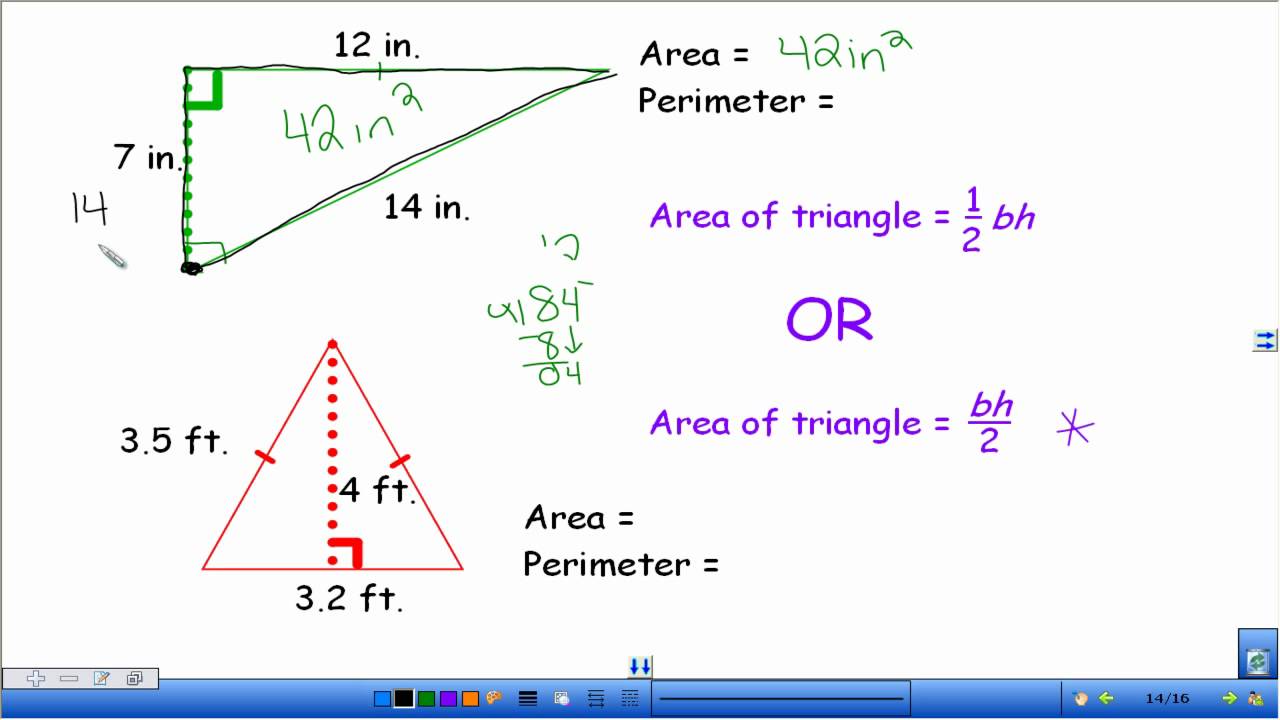
Topic what is the perimeter of this right triangle: Understanding the perimeter of a right triangle is essential for various math problems and real-life applications. In this article, we will explore the simple steps to calculate the perimeter, using the Pythagorean theorem and practical examples to ensure you grasp the concept easily and accurately.
Table of Content
- Understanding the Perimeter of a Right Triangle
- Introduction to Right Triangles
- Definition and Properties of a Right Triangle
- Understanding the Perimeter
- Formula for the Perimeter of a Right Triangle
- Using the Pythagorean Theorem
- Step-by-Step Calculation of the Perimeter
- Examples and Practice Problems
- Common Mistakes and How to Avoid Them
- Real-Life Applications of Right Triangles
- Advanced Concepts: Perimeter in Coordinate Geometry
- Summary and Key Takeaways
- Frequently Asked Questions (FAQs)
- YOUTUBE: Video này hướng dẫn cách tính diện tích và chu vi của một tam giác vuông. Thích hợp cho những người đang tìm hiểu về chu vi của tam giác vuông.
Understanding the Perimeter of a Right Triangle
A right triangle is a type of triangle that has one angle measuring 90 degrees. The sides of a right triangle are composed of the hypotenuse, which is the longest side, and the two legs, which are perpendicular to each other.
Formula for the Perimeter
The perimeter of a right triangle is the sum of the lengths of all three sides. If the lengths of the two legs are \(a\) and \(b\), and the hypotenuse is \(c\), the perimeter \(P\) is given by:
\[
P = a + b + c
\]
Calculating the Hypotenuse
To find the hypotenuse \(c\) when you know the lengths of the legs \(a\) and \(b\), use the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
Example Calculation
Consider a right triangle with legs of lengths 3 units and 4 units. To find the perimeter, follow these steps:
- Calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Sum the lengths of all three sides to get the perimeter:
\[
P = 3 + 4 + 5 = 12 \, \text{units}
\]
Table of Common Right Triangles
| Leg 1 (a) | Leg 2 (b) | Hypotenuse (c) | Perimeter (P) |
|---|---|---|---|
| 3 | 4 | 5 | 12 |
| 5 | 12 | 13 | 30 |
| 8 | 15 | 17 | 40 |
By following these steps, you can easily calculate the perimeter of any right triangle as long as you know the lengths of the two legs.

READ MORE:
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring exactly 90 degrees. This property makes right triangles unique and gives them several important characteristics and applications in mathematics and real life.
Here are some key features of right triangles:
- Hypotenuse: The side opposite the right angle, and it is the longest side of the triangle.
- Legs: The two sides that form the right angle. These are usually labeled as \(a\) and \(b\).
- Right Angle: An angle of 90 degrees, denoted by a small square at the vertex.
To better understand right triangles, let's look at their properties step-by-step:
- Pythagorean Theorem: This fundamental theorem states that for a right triangle, the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)):
\[
c^2 = a^2 + b^2
\] - Perimeter: The perimeter of a right triangle is the sum of the lengths of all three sides. Given the legs \(a\) and \(b\) and the hypotenuse \(c\), the perimeter \(P\) is:
\[
P = a + b + c
\] - Area: The area of a right triangle is half the product of the lengths of the two legs:
\[
\text{Area} = \frac{1}{2}ab
\]
Right triangles are widely used in various fields such as trigonometry, geometry, physics, engineering, and many real-world applications. Understanding the basics of right triangles is essential for solving numerous mathematical problems and practical challenges.
Definition and Properties of a Right Triangle
A right triangle is a type of triangle that has one of its interior angles measuring exactly 90 degrees. This 90-degree angle is known as the right angle, and it is a key characteristic that defines right triangles. The side opposite the right angle is the hypotenuse, the longest side of the triangle, while the other two sides are called the legs.
Here are the main properties of right triangles:
- Right Angle: One of the angles is exactly 90 degrees, forming a perfect L-shape.
- Hypotenuse: The side opposite the right angle, which is the longest side of the triangle.
- Legs: The two sides that form the right angle. These sides are perpendicular to each other.
To better understand these properties, consider the following aspects step-by-step:
- Pythagorean Theorem: This theorem is fundamental to right triangles. It states that the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the two legs (\(a\) and \(b\)):
\[
c^2 = a^2 + b^2
\] - Trigonometric Ratios: Right triangles are the basis for defining sine, cosine, and tangent functions, which are ratios of the lengths of the sides:
- \(\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{a}{c}\)
- \(\cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{b}{c}\)
- \(\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{a}{b}\)
- Perimeter: The perimeter of a right triangle is the sum of the lengths of all three sides. Given the legs \(a\) and \(b\) and the hypotenuse \(c\), the perimeter \(P\) is:
\[
P = a + b + c
\] - Area: The area of a right triangle is half the product of the lengths of the two legs:
\[
\text{Area} = \frac{1}{2}ab
\]
Right triangles are fundamental in mathematics and have numerous applications in various fields, including trigonometry, geometry, physics, and engineering. Understanding their properties is essential for solving many practical and theoretical problems.
Understanding the Perimeter
The perimeter of a triangle is the total length around the triangle, which is the sum of the lengths of all its sides. For a right triangle, the perimeter involves the lengths of the two legs and the hypotenuse.
To calculate the perimeter of a right triangle, you need to know the lengths of its three sides: the two legs (commonly denoted as \(a\) and \(b\)) and the hypotenuse (denoted as \(c\)). The formula for the perimeter \(P\) of a right triangle is:
\[
P = a + b + c
\]
Here is a step-by-step guide to understanding and calculating the perimeter of a right triangle:
- Identify the lengths of the legs: Determine the lengths of the two legs \(a\) and \(b\). These are the sides that form the right angle.
- Calculate the hypotenuse: If the hypotenuse \(c\) is not given, use the Pythagorean theorem to find it:
\[
c = \sqrt{a^2 + b^2}
\] - Sum the side lengths: Add the lengths of the two legs and the hypotenuse to get the perimeter:
\[
P = a + b + c
\]
Let's look at an example:
- Example: Consider a right triangle with legs \(a = 3\) units and \(b = 4\) units.
- Calculate the hypotenuse using the Pythagorean theorem:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Sum the lengths of all sides to find the perimeter:
\[
P = 3 + 4 + 5 = 12 \, \text{units}
\]
- Calculate the hypotenuse using the Pythagorean theorem:
By following these steps, you can easily determine the perimeter of any right triangle, which is crucial for solving various mathematical problems and real-life applications.
Formula for the Perimeter of a Right Triangle
The perimeter of a right triangle is the total distance around the triangle, which is the sum of the lengths of its three sides: the two legs and the hypotenuse. The formula to calculate the perimeter is straightforward and involves simple addition once all side lengths are known.
The general formula for the perimeter \(P\) of a right triangle with legs \(a\) and \(b\), and hypotenuse \(c\) is:
\[
P = a + b + c
\]
To apply this formula, follow these steps:
- Identify the lengths of the legs: Determine the lengths of the two legs \(a\) and \(b\). These are the sides that form the right angle.
- Calculate the hypotenuse: If the hypotenuse \(c\) is not given, use the Pythagorean theorem to find it:
\[
c = \sqrt{a^2 + b^2}
\] - Sum the side lengths: Add the lengths of the two legs and the hypotenuse to get the perimeter:
\[
P = a + b + c
\]
Let's illustrate this with an example:
- Example: Consider a right triangle with legs \(a = 5\) units and \(b = 12\) units.
- Calculate the hypotenuse using the Pythagorean theorem:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
\] - Sum the lengths of all sides to find the perimeter:
\[
P = 5 + 12 + 13 = 30 \, \text{units}
\]
- Calculate the hypotenuse using the Pythagorean theorem:
Using these steps and the formula, you can easily determine the perimeter of any right triangle, making it a simple yet essential calculation in geometry and various practical applications.
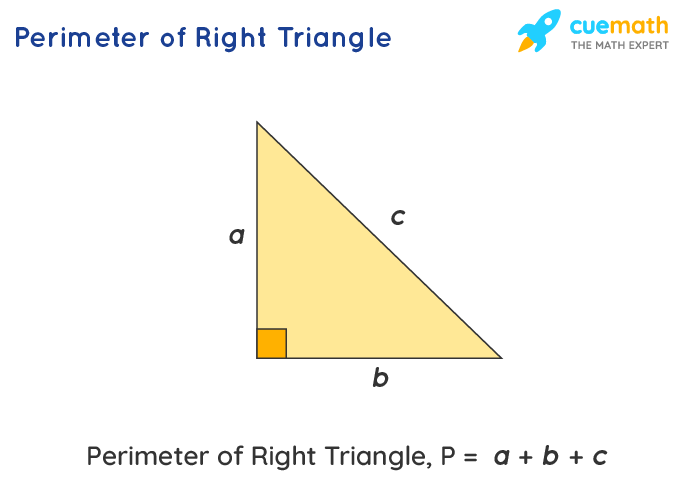
Using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental principle in geometry that relates the lengths of the sides of a right triangle. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem is expressed as:
\[
c^2 = a^2 + b^2
\]
Where:
- \(c\) is the length of the hypotenuse
- \(a\) and \(b\) are the lengths of the other two sides
Here’s how to use the Pythagorean Theorem step-by-step:
- Identify the sides: Determine which sides of the triangle are the legs (\(a\) and \(b\)) and which is the hypotenuse (\(c\)). The hypotenuse is always opposite the right angle and is the longest side.
- Apply the Pythagorean Theorem: Substitute the known values into the theorem. If you need to find the hypotenuse, solve for \(c\):
\[
c = \sqrt{a^2 + b^2}
\] - Solve for the unknown side: If you are given the hypotenuse and one leg and need to find the other leg, rearrange the theorem to solve for the missing side:
or
\[
a = \sqrt{c^2 - b^2}
\]
\[
b = \sqrt{c^2 - a^2}
\] - Calculate the perimeter: Once you have all three sides, add them together to find the perimeter:
\[
P = a + b + c
\]
Let's look at an example:
- Example: Suppose we have a right triangle with one leg \(a = 6\) units and the other leg \(b = 8\) units.
- Calculate the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
\] - Sum the lengths of all sides to find the perimeter:
\[
P = 6 + 8 + 10 = 24 \, \text{units}
\]
- Calculate the hypotenuse using the Pythagorean Theorem:
By using the Pythagorean Theorem, you can easily find the lengths of the sides of a right triangle and subsequently calculate its perimeter. This theorem is a powerful tool in geometry, providing a straightforward method to solve various problems involving right triangles.
Step-by-Step Calculation of the Perimeter
Calculating the perimeter of a right triangle involves summing the lengths of its three sides: the two legs and the hypotenuse. Here’s a detailed, step-by-step guide to finding the perimeter of a right triangle:
- Identify the lengths of the legs: Determine the lengths of the two legs \(a\) and \(b\). These sides form the right angle of the triangle.
- Calculate the hypotenuse: If the hypotenuse \(c\) is not provided, use the Pythagorean Theorem to calculate it. The theorem states:
\[
c = \sqrt{a^2 + b^2}
\]For example, if \(a = 3\) units and \(b = 4\) units, then:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{units}
\] - Sum the side lengths: Add the lengths of the two legs and the hypotenuse to find the perimeter \(P\):
\[
P = a + b + c
\]Using the example above, with \(a = 3\) units, \(b = 4\) units, and \(c = 5\) units:
\[
P = 3 + 4 + 5 = 12 \, \text{units}
\]
Let’s look at another example:
- Example: Consider a right triangle with legs \(a = 7\) units and \(b = 24\) units.
- Calculate the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \, \text{units}
\] - Sum the lengths of all sides to find the perimeter:
\[
P = 7 + 24 + 25 = 56 \, \text{units}
\]
- Calculate the hypotenuse using the Pythagorean Theorem:
By following these steps, you can accurately calculate the perimeter of any right triangle. This process is essential for solving various geometric problems and understanding the properties of right triangles.
Examples and Practice Problems
Practicing with examples and problems is an effective way to understand how to calculate the perimeter of a right triangle. Here, we provide several examples and practice problems to help you master this concept.
Example 1
Consider a right triangle with legs \(a = 6\) units and \(b = 8\) units. Calculate the hypotenuse and the perimeter.
- Calculate the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{units}
\] - Calculate the perimeter:
\[
P = 6 + 8 + 10 = 24 \, \text{units}
\]
Example 2
Consider a right triangle with legs \(a = 9\) units and \(b = 12\) units. Calculate the hypotenuse and the perimeter.
- Calculate the hypotenuse using the Pythagorean Theorem:
\[
c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \, \text{units}
\] - Calculate the perimeter:
\[
P = 9 + 12 + 15 = 36 \, \text{units}
\]
Practice Problems
Try solving these practice problems to reinforce your understanding:
- Problem 1: A right triangle has legs \(a = 5\) units and \(b = 12\) units. Calculate the hypotenuse and the perimeter.
- Problem 2: A right triangle has legs \(a = 7\) units and \(b = 24\) units. Calculate the hypotenuse and the perimeter.
- Problem 3: A right triangle has legs \(a = 8\) units and \(b = 15\) units. Calculate the hypotenuse and the perimeter.
- Problem 4: A right triangle has legs \(a = 10\) units and \(b = 24\) units. Calculate the hypotenuse and the perimeter.
Solution to Practice Problems
Check your answers with the solutions provided:
- Solution to Problem 1:
- Hypotenuse:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \, \text{units}
\] - Perimeter:
\[
P = 5 + 12 + 13 = 30 \, \text{units}
\]
- Hypotenuse:
- Solution to Problem 2:
- Hypotenuse:
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \, \text{units}
\] - Perimeter:
\[
P = 7 + 24 + 25 = 56 \, \text{units}
\]
- Hypotenuse:
- Solution to Problem 3:
- Hypotenuse:
\[
c = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17 \, \text{units}
\] - Perimeter:
\[
P = 8 + 15 + 17 = 40 \, \text{units}
\]
- Hypotenuse:
- Solution to Problem 4:
- Hypotenuse:
\[
c = \sqrt{10^2 + 24^2} = \sqrt{100 + 576} = \sqrt{676} = 26 \, \text{units}
\] - Perimeter:
\[
P = 10 + 24 + 26 = 60 \, \text{units}
\]
- Hypotenuse:
Common Mistakes and How to Avoid Them
Calculating the perimeter of a right triangle is straightforward, but there are several common mistakes that students often make. Here, we will discuss these mistakes and provide tips on how to avoid them.
-
Not Using the Pythagorean Theorem Correctly
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The formula is:
\( c^2 = a^2 + b^2 \)
Tip: Ensure you correctly identify the hypotenuse (the longest side) and apply the formula accurately. Double-check your calculations to avoid errors.
-
Incorrectly Adding the Sides
Remember, the perimeter is the sum of all three sides:
\( P = a + b + c \)
Tip: Clearly label each side and carefully add them together. Ensure you do not miss any side or include any incorrect values.
-
Confusing Area and Perimeter
The area and perimeter are different properties. The area measures the surface within the triangle, while the perimeter is the total length around the triangle.
Tip: Use the correct formula for the perimeter. For the area of a right triangle, the formula is:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
For the perimeter, stick to:
\( P = a + b + c \)
-
Not Finding the Missing Side First
If only two sides are given, you need to find the third side using the Pythagorean Theorem before calculating the perimeter.
Tip: Always find the missing side first if not all sides are provided. For example, if you know \( a \) and \( b \), calculate \( c \) using:
\( c = \sqrt{a^2 + b^2} \)
-
Rounding Errors
Rounding intermediate values too early can lead to inaccuracies in the final perimeter calculation.
Tip: Avoid rounding until the final step. Use the full precision of your calculator during intermediate steps.
-
Mislabeling Sides
Mixing up which sides are the legs and which is the hypotenuse can lead to incorrect calculations.
Tip: Clearly mark the legs (the two shorter sides) and the hypotenuse (the longest side) before performing calculations.
By keeping these tips in mind, you can avoid common mistakes and ensure accurate calculation of the perimeter of right triangles.

Real-Life Applications of Right Triangles
Right triangles have various practical applications in everyday life. Their properties are used in fields ranging from architecture to navigation. Here are some common real-life applications:
- Architecture and Construction
Right triangles are fundamental in the design and construction of buildings. Architects and engineers use them to calculate structural loads, angles, and the slope of roofs. For example:
- Roofs: The pitch of a roof is often expressed as the ratio of the rise (vertical height) over the run (horizontal distance). Using the properties of right triangles, the pitch can be calculated accurately to ensure proper water drainage and structural stability.
- Trusses: Triangular trusses are used in bridges and buildings to distribute weight evenly, providing strength and stability.
- Navigation
Right triangles are used in navigation to determine distances and directions. Sailors and pilots use them to plot courses and bearings:
- Bearing: This is the direction from one point to another, measured in degrees clockwise from north. By using the trigonometric relationships in right triangles, navigators can determine their position relative to a landmark or destination.
- Surveying
Surveyors use right triangles to measure land and determine property boundaries. By creating a right triangle between two known points and a third point, they can calculate distances and angles accurately.
- Sailing
Triangular sails, such as the lateen sail, are designed using right triangle principles. These sails allow boats to catch wind more effectively from different angles, improving maneuverability and speed.
- Art and Design
Right triangles are often used in art to create perspective and balance. For example, the famous painting "The Last Supper" by Leonardo da Vinci uses right triangles to draw the viewer's eye to the central figure of Jesus Christ.
In summary, the properties of right triangles are utilized in various practical applications, making them an essential part of many fields. Understanding these applications helps in appreciating the importance of right triangles in everyday life.
Advanced Concepts: Perimeter in Coordinate Geometry
Calculating the perimeter of a right triangle using coordinate geometry involves a series of steps. Here’s a detailed guide to help you understand and perform these calculations accurately.
Let's consider a right triangle with vertices A(\(x_1\), \(y_1\)), B(\(x_2\), \(y_2\)), and C(\(x_3\), \(y_3\)). To find the perimeter, we need to calculate the lengths of all three sides using the distance formula and then sum these lengths.
-
Calculate the length of side AB:
The formula to calculate the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is:
$$ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
Plug in the coordinates of points A and B to find the length of AB.
-
Calculate the length of side BC:
Using the same distance formula, calculate the distance between points B and C:
$$ BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} $$
Plug in the coordinates of points B and C to find the length of BC.
-
Calculate the length of side AC:
Finally, use the distance formula to calculate the distance between points A and C:
$$ AC = \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2} $$
Plug in the coordinates of points A and C to find the length of AC.
-
Sum the lengths to find the perimeter:
Once you have the lengths of all three sides, add them together to get the perimeter:
$$ \text{Perimeter} = AB + BC + AC $$
Here's an example to illustrate these steps:
- Let’s say the vertices of the triangle are A(1, 2), B(4, 6), and C(1, 6).
- First, calculate AB: $$ AB = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$
- Next, calculate BC: $$ BC = \sqrt{(1 - 4)^2 + (6 - 6)^2} = \sqrt{(-3)^2 + 0^2} = \sqrt{9} = 3 $$
- Finally, calculate AC: $$ AC = \sqrt{(1 - 1)^2 + (6 - 2)^2} = \sqrt{0 + 4^2} = \sqrt{16} = 4 $$
- The perimeter is then: $$ \text{Perimeter} = 5 + 3 + 4 = 12 $$
By following these steps, you can accurately determine the perimeter of any right triangle given its vertices in a coordinate plane.
Summary and Key Takeaways
The perimeter of a right triangle is a fundamental concept in geometry, combining understanding of triangle properties with practical mathematical application. Here’s a concise summary of key points:
- The perimeter of a right triangle is the total length around the triangle, calculated by summing the lengths of all three sides.
- For a right triangle with legs \( a \) and \( b \), and hypotenuse \( c \), the perimeter is given by: \( P = a + b + c \).
- The Pythagorean Theorem is essential for calculating the hypotenuse if only the lengths of the legs are known: \( c = \sqrt{a^2 + b^2} \).
- Once the hypotenuse is determined, the perimeter can be computed by simply adding the lengths of all sides: \( P = a + b + \sqrt{a^2 + b^2} \).
- Right triangles can be categorized into special cases, such as isosceles right triangles, where the two legs are equal, simplifying the calculation of the perimeter.
In practical applications, understanding the perimeter of right triangles can be useful in fields such as architecture, engineering, and various forms of design, where accurate measurements and geometric calculations are crucial.
To avoid common mistakes:
- Ensure that all side lengths are measured in the same units before performing calculations.
- Verify calculations using the Pythagorean theorem to avoid errors in finding the hypotenuse.
- Double-check each step in the calculation to confirm the accuracy of the perimeter.
By mastering these concepts and steps, calculating the perimeter of right triangles becomes a straightforward task, enabling you to solve a wide range of problems both in academic contexts and real-world scenarios.
Frequently Asked Questions (FAQs)
Here are some commonly asked questions about the perimeter of right triangles:
-
What is the perimeter of a right triangle?
The perimeter of a right triangle is the sum of the lengths of its three sides. If the sides are denoted as \( a \), \( b \), and \( c \) (where \( c \) is the hypotenuse), then the perimeter \( P \) is given by:
\[ P = a + b + c \]
-
How can I find the perimeter if only two sides are known?
To find the perimeter when only two sides of a right triangle are known, you can use the Pythagorean Theorem to find the third side. The Pythagorean Theorem states:
\[ c^2 = a^2 + b^2 \]
After finding the length of the third side, sum all three sides to get the perimeter:
\[ P = a + b + c \]
-
What is the Pythagorean Theorem?
The Pythagorean Theorem relates the sides of a right triangle. It states that the square of the hypotenuse (\( c \)) is equal to the sum of the squares of the other two sides (\( a \) and \( b \)):
\[ c^2 = a^2 + b^2 \]
-
How do I calculate the perimeter of a right triangle using the Pythagorean Theorem?
First, use the Pythagorean Theorem to find the hypotenuse or the missing side:
\[ c = \sqrt{a^2 + b^2} \]
Then, add up the lengths of all three sides to find the perimeter:
\[ P = a + b + c \]
-
What are some examples of calculating the perimeter of right triangles?
Example 1: If a right triangle has sides of lengths 3, 4, and 5, the perimeter is:
\[ P = 3 + 4 + 5 = 12 \]
Example 2: For a right triangle with a base of 6 units and a height of 8 units, find the hypotenuse using:
\[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 \]
The perimeter is then:
\[ P = 6 + 8 + 10 = 24 \]
-
What is the difference between the area and the perimeter of a right triangle?
The perimeter of a right triangle is the total length around the triangle, calculated by summing its three sides. The area measures the space within the triangle, given by:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Video này hướng dẫn cách tính diện tích và chu vi của một tam giác vuông. Thích hợp cho những người đang tìm hiểu về chu vi của tam giác vuông.
Diện tích và chu vi của tam giác vuông | Toán học với thầy J
READ MORE:
Video này hướng dẫn cách tính chu vi của một tam giác vuông một cách tinh tế và chi tiết. Thích hợp cho những người đang tìm hiểu về chu vi của tam giác vuông.
Cách tinh tế để tìm chu vi của tam giác vuông | (giải thích từng bước) | #toán #toán học