Topic area perimeter volume: Explore our comprehensive guide on area, perimeter, and volume. Understand the fundamental concepts, learn essential formulas, and discover practical applications in real-life scenarios. Perfect for students, educators, and anyone looking to enhance their mathematical skills. Dive in and master these crucial measurements today!
Table of Content
- Area, Perimeter, and Volume: Comprehensive Guide
- Introduction to Area, Perimeter, and Volume
- Basic Concepts and Definitions
- Formulas and Calculations
- Applications in Real Life
- Understanding Area
- Common Shapes and Their Areas
- Advanced Area Calculations
- Understanding Perimeter
- Common Shapes and Their Perimeters
- Advanced Perimeter Calculations
- Understanding Volume
- Common Shapes and Their Volumes
- Advanced Volume Calculations
- Area Practice Problems
- Perimeter Practice Problems
- Volume Practice Problems
- Summary and Review
- YOUTUBE: Giải thích chu vi, diện tích, và thể tích một cách dễ hiểu với Thầy J. Tìm hiểu về các khái niệm toán học cơ bản này qua video.
Area, Perimeter, and Volume: Comprehensive Guide
Understanding the concepts of area, perimeter, and volume is essential in various fields, including mathematics, engineering, and architecture. These measurements help us quantify the space within and around different shapes and objects. This guide provides a detailed overview of each concept along with practice problems to enhance your learning experience.
Area
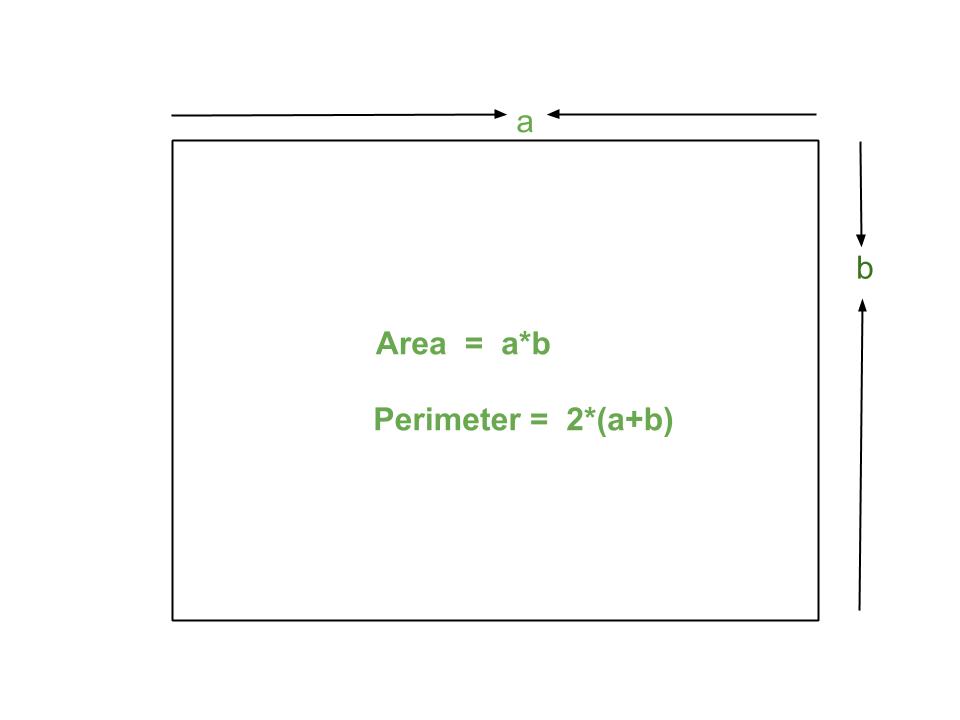
The area of a shape is the measure of the space enclosed within its boundaries. It is expressed in square units.
- Rectangle: \( A = l \times w \) where \( l \) is the length and \( w \) is the width.
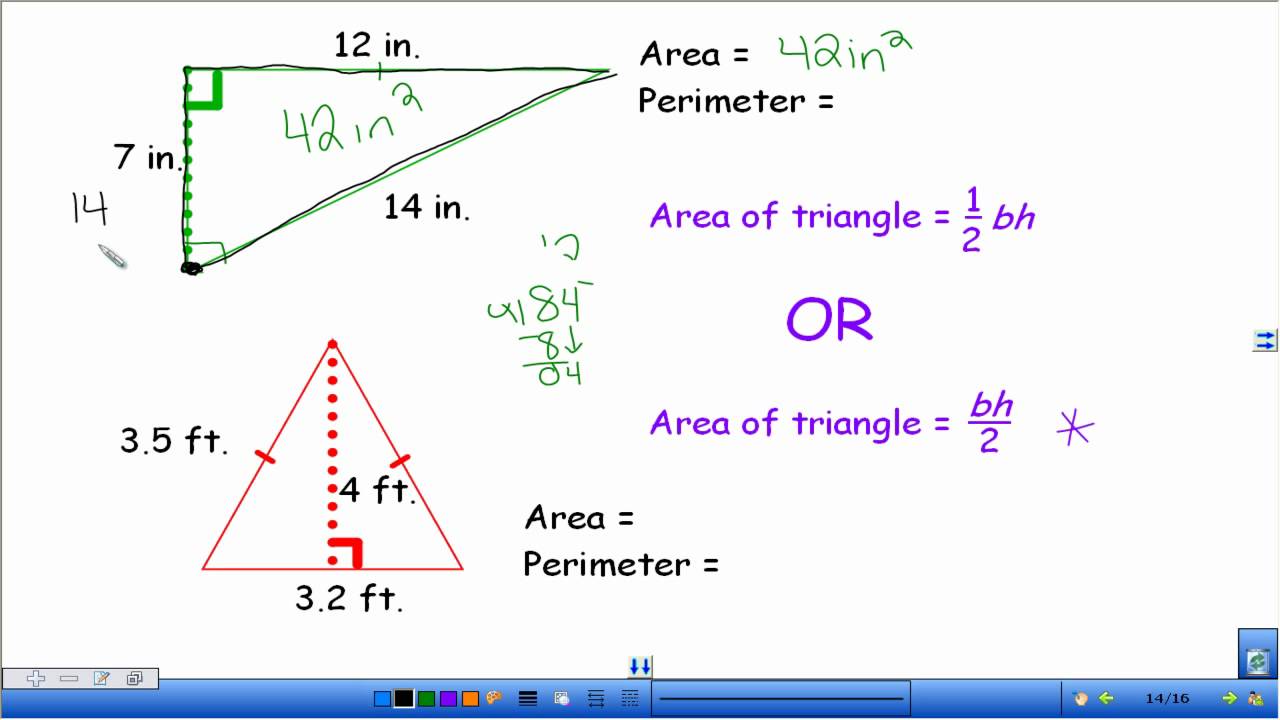
- Triangle: \( A = \frac{1}{2} \times b \times h \) where \( b \) is the base and \( h \) is the height.
- Circle: \( A = \pi r^2 \) where \( r \) is the radius.
Perimeter
The perimeter of a shape is the total distance around its edges. It is expressed in linear units.
- Rectangle: \( P = 2l + 2w \)
- Triangle: \( P = a + b + c \) where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Circle (Circumference): \( P = 2\pi r \)
Volume
Volume is the measure of the space occupied by a three-dimensional object. It is expressed in cubic units.
- Cuboid: \( V = l \times w \times h \)
- Cylinder: \( V = \pi r^2 h \)
- Sphere: \( V = \frac{4}{3} \pi r^3 \)
Practice Problems
- Calculate the area and perimeter of a rectangle with a length of 8 units and a width of 5 units.
- Find the area of a triangle with a base of 10 units and a height of 6 units.
- Determine the volume of a cuboid with dimensions 4 units, 3 units, and 2 units.
- What is the circumference of a circle with a radius of 7 units?
- Calculate the volume of a sphere with a radius of 5 units.
Summary
Mastering the concepts of area, perimeter, and volume is fundamental for solving a variety of real-world problems. Practice regularly to improve your skills and confidence in these areas.

READ MORE:
Introduction to Area, Perimeter, and Volume
Understanding the concepts of area, perimeter, and volume is essential in geometry and everyday applications. These measurements help us quantify the space within a shape, the distance around it, and the capacity of three-dimensional objects.
Area refers to the amount of space inside the boundary of a two-dimensional shape. The formula for the area depends on the shape:
- Square: \( A = s^2 \)
- Rectangle: \( A = l \times w \)
- Triangle: \( A = \frac{1}{2} \times b \times h \)
- Circle: \( A = \pi r^2 \)
- Parallelogram: \( A = b \times h \)
- Trapezoid: \( A = \frac{1}{2} \times (b_1 + b_2) \times h \)
Perimeter is the total distance around the boundary of a two-dimensional shape:
- Square: \( P = 4s \)
- Rectangle: \( P = 2(l + w) \)
- Triangle: \( P = a + b + c \)
- Circle (Circumference): \( C = 2\pi r \)
Volume measures the space a three-dimensional object occupies. Here are the formulas for common shapes:
- Cube: \( V = s^3 \)
- Rectangular Prism: \( V = l \times w \times h \)
- Cylinder: \( V = \pi r^2 h \)
- Sphere: \( V = \frac{4}{3} \pi r^3 \)
- Cone: \( V = \frac{1}{3} \pi r^2 h \)
- Pyramid: \( V = \frac{1}{3} \times \text{Base Area} \times h \)
Mastering these basic formulas allows for solving practical problems in construction, crafting, and various fields requiring spatial calculations.
Basic Concepts and Definitions
The concepts of area, perimeter, and volume are fundamental in geometry, allowing us to measure the extent and boundaries of two-dimensional shapes and three-dimensional objects.
Area
The area of a shape is the measure of the space it occupies in a plane. It is measured in square units (e.g., square meters, square centimeters).
To calculate the area, we use different formulas depending on the shape:
- Square: \( A = a^2 \) where \( a \) is the side length.
- Rectangle: \( A = l \times w \) where \( l \) is the length and \( w \) is the width.
- Triangle: \( A = \frac{1}{2} \times b \times h \) where \( b \) is the base and \( h \) is the height.
- Circle: \( A = \pi r^2 \) where \( r \) is the radius.
Perimeter
The perimeter of a shape is the total length of its boundaries. It is measured in linear units (e.g., meters, centimeters).
To calculate the perimeter, we sum the lengths of all the sides of the shape:
- Square: \( P = 4a \) where \( a \) is the side length.
- Rectangle: \( P = 2l + 2w \) where \( l \) is the length and \( w \) is the width.
- Triangle: \( P = a + b + c \) where \( a \), \( b \), and \( c \) are the side lengths.
- Circle: \( P = 2\pi r \) where \( r \) is the radius (also known as the circumference).
Volume
The volume of an object is the measure of the space it occupies in three dimensions. It is measured in cubic units (e.g., cubic meters, cubic centimeters).
To calculate the volume, we use different formulas depending on the shape:
- Cuboid: \( V = l \times w \times h \) where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- Cube: \( V = a^3 \) where \( a \) is the side length.
- Cylinder: \( V = \pi r^2 h \) where \( r \) is the radius and \( h \) is the height.
- Sphere: \( V = \frac{4}{3} \pi r^3 \) where \( r \) is the radius.
Summary
Understanding these basic concepts and their respective formulas is crucial for solving various mathematical problems and applying them in real-life scenarios, such as construction, architecture, and any field involving measurements.
Formulas and Calculations
Understanding the formulas and calculations for area, perimeter, and volume is essential for solving various geometric problems. Below are the key formulas for different shapes.
Area
- Square: \( A = a^2 \)
(where \( a \) is the length of a side) - Rectangle: \( A = l \times w \)
(where \( l \) is the length and \( w \) is the width) - Triangle: \( A = \frac{1}{2} b \times h \)
(where \( b \) is the base and \( h \) is the height) - Circle: \( A = \pi r^2 \)
(where \( r \) is the radius) - Trapezoid: \( A = \frac{1}{2} (b_1 + b_2) \times h \)
(where \( b_1 \) and \( b_2 \) are the lengths of the parallel sides and \( h \) is the height)
Perimeter
- Square: \( P = 4a \)
(where \( a \) is the length of a side) - Rectangle: \( P = 2(l + w) \)
(where \( l \) is the length and \( w \) is the width) - Triangle: \( P = a + b + c \)
(where \( a \), \( b \), and \( c \) are the lengths of the sides) - Circle (Circumference): \( P = 2\pi r \)
(where \( r \) is the radius)
Volume
- Cube: \( V = a^3 \)
(where \( a \) is the length of an edge) - Rectangular Prism: \( V = l \times w \times h \)
(where \( l \) is the length, \( w \) is the width, and \( h \) is the height) - Cylinder: \( V = \pi r^2 h \)
(where \( r \) is the radius and \( h \) is the height) - Sphere: \( V = \frac{4}{3} \pi r^3 \)
(where \( r \) is the radius) - Pyramid: \( V = \frac{1}{3} A_b h \)
(where \( A_b \) is the area of the base and \( h \) is the height) - Cone: \( V = \frac{1}{3} \pi r^2 h \)
(where \( r \) is the radius and \( h \) is the height)
Example Calculations
Example 1: Calculate the area of a rectangle with a length of 5 meters and a width of 3 meters.
Using the formula \( A = l \times w \), we get:
\( A = 5 \times 3 = 15 \text{ square meters} \)
Example 2: Calculate the volume of a cylinder with a radius of 4 meters and a height of 10 meters.
Using the formula \( V = \pi r^2 h \), we get:
\( V = \pi \times 4^2 \times 10 = 160 \pi \text{ cubic meters} \)
These formulas and example calculations provide a solid foundation for understanding and applying geometric principles in various contexts.
Applications in Real Life
Understanding the concepts of area, perimeter, and volume is not just confined to academic exercises. These measurements have a wide range of practical applications in real life, helping in various fields such as construction, landscaping, agriculture, and more.
Perimeter
- Gardening: When building a fence around a garden to keep animals out, you need to calculate the perimeter to determine the amount of fencing material required. For example, if your garden is 20 feet long and 30 feet wide, the perimeter would be \(2 \times (20 + 30) = 100\) feet.
- Construction: In construction projects, knowing the perimeter is essential for tasks such as laying the foundation of a building or determining the amount of materials needed for the border of a structure.
- Surveying: Surveyors use the perimeter to measure land plots, helping in property division and determining the amount of fencing needed for properties.
Area
- Landscaping: The area is used to calculate the amount of grass seed or sod needed to cover a lawn. For a rectangular lawn, the area is calculated by multiplying the length and width.
- Painting and Flooring: When painting walls or installing flooring, calculating the area helps in estimating the amount of paint or flooring material required. For example, to paint a wall 15 feet long and 10 feet high, the area would be \(15 \times 10 = 150\) square feet.
- Agriculture: Farmers use area calculations to determine the size of their fields, which helps in planning crop planting and estimating yield.
Volume
- Storage and Capacity: Calculating the volume of containers helps in determining how much they can hold. For example, the volume of a rectangular box is found by multiplying its length, width, and height.
- Water Tanks and Pools: Knowing the volume of water tanks or swimming pools is crucial for understanding how much water they can store. For a cylindrical tank, the volume is calculated using the formula \(V = \pi r^2 h\).
- Cooking: Volume measurements are essential in cooking and baking to determine the amount of ingredients needed. Recipes often require precise volume measurements to ensure the correct consistency and taste.
In summary, the practical applications of area, perimeter, and volume are extensive and diverse, impacting everyday activities and various professional fields. Mastering these concepts not only enhances mathematical skills but also equips individuals with essential tools for solving real-world problems.

Understanding Area
Area is a fundamental concept in geometry that refers to the measure of the amount of space inside a two-dimensional shape. Understanding the area is crucial for various real-world applications, such as determining the size of a plot of land, the amount of paint needed for a wall, or the fabric required to make a piece of clothing. The unit of area is typically expressed in square units, such as square meters (m²), square centimeters (cm²), or square feet (ft²).
Basic Principles of Area
- Definition: The area is the measure of the surface enclosed within the boundary of a two-dimensional shape.
- Measurement Units: Common units of area include square meters (m²), square centimeters (cm²), square inches (in²), and square feet (ft²).
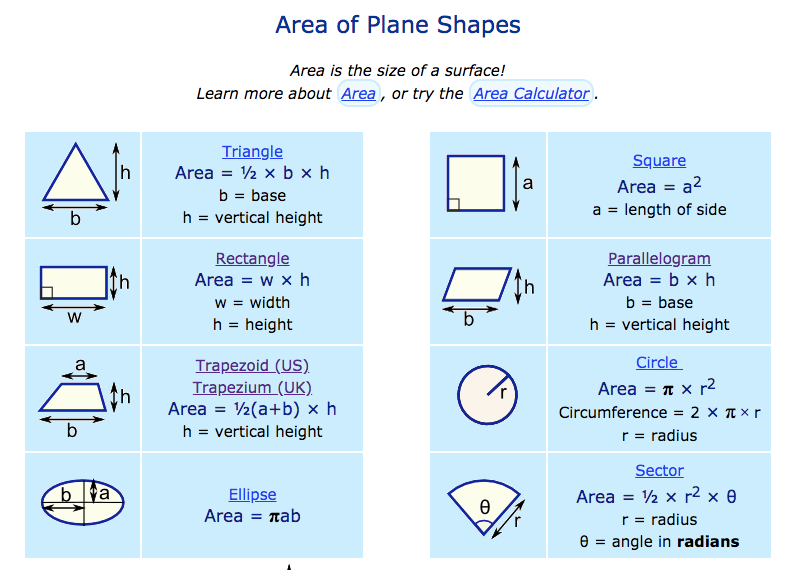
Area of Common Shapes
| Shape | Formula | Explanation |
|---|---|---|
| Square | \( A = s^2 \) | The area of a square is calculated by squaring the length of one of its sides. |
| Rectangle | \( A = l \times w \) | The area of a rectangle is found by multiplying its length by its width. |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | The area of a triangle is half the product of its base and height. |
| Circle | \( A = \pi r^2 \) | The area of a circle is π times the square of its radius. |
| Parallelogram | \( A = b \times h \) | The area of a parallelogram is the base times the height. |
| Trapezoid | \( A = \frac{1}{2} \times (a + b) \times h \) | The area of a trapezoid is half the sum of the bases times the height. |
Steps to Calculate Area
- Identify the shape of the area you need to calculate.
- Measure the necessary dimensions (e.g., length, width, height, radius).
- Apply the appropriate formula for the shape.
- Calculate the product or sum as required by the formula.
- Express the result in square units.
Practical Examples
- Painting a Wall: To determine how much paint you need, calculate the area of the wall by multiplying its height by its width.
- Landscaping: When laying sod for a lawn, measure the length and width of the yard to calculate the area in square meters or feet.
- Carpeting a Room: Measure the length and width of the room to find out how much carpet you will need to cover the floor.
Understanding and calculating the area helps in various fields such as construction, interior design, and agriculture, making it a crucial skill in both academic and real-life contexts.
Common Shapes and Their Areas
Understanding the area of different shapes is crucial in geometry. Below are the formulas and explanations for calculating the area of some common shapes:
-
Rectangle:
- Formula: \( \text{Area} = l \times w \)
- Explanation: The area is found by multiplying the length (\( l \)) and the width (\( w \)) of the rectangle.
-
Square:
- Formula: \( \text{Area} = a^2 \)
- Explanation: The area is the square of the length of one side (\( a \)).
-
Triangle:
- Formula: \( \text{Area} = \frac{1}{2} \times b \times h \)
- Explanation: The area is half the product of the base (\( b \)) and the height (\( h \)).
-
Circle:
- Formula: \( \text{Area} = \pi r^2 \)
- Explanation: The area is the product of pi (\( \pi \)) and the square of the radius (\( r \)).
-
Parallelogram:
- Formula: \( \text{Area} = b \times h \)
- Explanation: The area is found by multiplying the base (\( b \)) and the height (\( h \)).
-
Trapezoid (US) / Trapezium (UK):
- Formula: \( \text{Area} = \frac{1}{2} \times (a + b) \times h \)
- Explanation: The area is half the product of the sum of the parallel sides (\( a \) and \( b \)) and the height (\( h \)).
-
Ellipse:
- Formula: \( \text{Area} = \pi a b \)
- Explanation: The area is the product of pi (\( \pi \)), the semi-major axis (\( a \)), and the semi-minor axis (\( b \)).
-
Sector of a Circle:
- Formula: \( \text{Area} = \frac{1}{2} \times r^2 \times \theta \)
- Explanation: The area is half the product of the square of the radius (\( r \)) and the angle in radians (\( \theta \)).
Advanced Area Calculations
Advanced area calculations often involve complex shapes or multiple figures. Understanding these calculations requires breaking down shapes into simpler components, applying formulas, and summing the results. Here, we delve into some advanced concepts and provide examples to illustrate these calculations.
Composite Shapes
Composite shapes are made up of two or more basic shapes. To find the area of a composite shape:
- Divide the composite shape into simpler shapes.
- Calculate the area of each simple shape.
- Add the areas of the simple shapes to get the total area.
For example, consider a shape made up of a rectangle and a semicircle:
- Rectangle: length = 8 cm, width = 4 cm
- Semicircle: radius = 2 cm
Area of the rectangle: \( A_{\text{rectangle}} = \text{length} \times \text{width} = 8 \, \text{cm} \times 4 \, \text{cm} = 32 \, \text{cm}^2 \)
Area of the semicircle: \( A_{\text{semicircle}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (2 \, \text{cm})^2 = 2 \pi \, \text{cm}^2 \)
Total area: \( A_{\text{total}} = A_{\text{rectangle}} + A_{\text{semicircle}} = 32 \, \text{cm}^2 + 2 \pi \, \text{cm}^2 \)
Irregular Shapes
For irregular shapes, one common method is to use a grid or coordinate system:
- Overlay a grid on the shape.
- Count the full squares within the shape.
- Estimate and sum the partial squares.
- Multiply the number of squares by the area of one square.
Using Calculus
Calculus can be applied to find the area under curves or irregular shapes:
- Set up the integral with the proper limits of integration.
- Integrate the function that represents the shape.
- Evaluate the definite integral to find the area.
Example: Find the area under the curve \( y = x^2 \) from \( x = 0 \) to \( x = 2 \):
Integral: \( \int_{0}^{2} x^2 \, dx \)
Evaluation: \( \left[ \frac{x^3}{3} \right]_{0}^{2} = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3} \)
Area: \( \frac{8}{3} \, \text{square units} \)
Parametric Equations
For shapes defined by parametric equations, the area can be found using:
- Set up the parametric equations: \( x(t) \) and \( y(t) \).
- Integrate the product of the derivatives: \( \int y(t) \frac{dx}{dt} \, dt \).
Example: For the parametric equations \( x(t) = \cos(t) \) and \( y(t) = \sin(t) \) over \( t = 0 \) to \( t = \pi \):
Integral: \( \int_{0}^{\pi} \sin(t) (-\sin(t)) \, dt = - \int_{0}^{\pi} \sin^2(t) \, dt \)
Using the identity \( \sin^2(t) = \frac{1 - \cos(2t)}{2} \):
Integral: \( - \int_{0}^{\pi} \frac{1 - \cos(2t)}{2} \, dt \)
Evaluation: \( - \left[ \frac{t}{2} - \frac{\sin(2t)}{4} \right]_{0}^{\pi} = - \left( \frac{\pi}{2} - 0 \right) = - \frac{\pi}{2} \)
Area: \( \frac{\pi}{2} \, \text{square units} \)
Applications of Advanced Area Calculations
These advanced techniques are crucial in various fields:
- Engineering: Designing and analyzing components with complex shapes.
- Architecture: Planning spaces and structures.
- Environmental Science: Measuring land areas and natural formations.
Understanding Perimeter
The perimeter of a shape is the total length of its boundary. It is a measure of the distance around the outer edge of a two-dimensional figure. The concept of perimeter is applied to various geometric shapes including rectangles, squares, triangles, and polygons.
Here are the basic formulas for calculating the perimeter of common shapes:
- Square: The perimeter of a square is calculated by adding up the lengths of all four sides. Since all sides of a square are equal, the formula is:
P = 4s
where s is the length of one side. - Rectangle: The perimeter of a rectangle is the sum of twice the width and twice the length:
P = 2l + 2w
where l is the length and w is the width. - Triangle: The perimeter of a triangle is the sum of the lengths of its three sides:
P = a + b + c
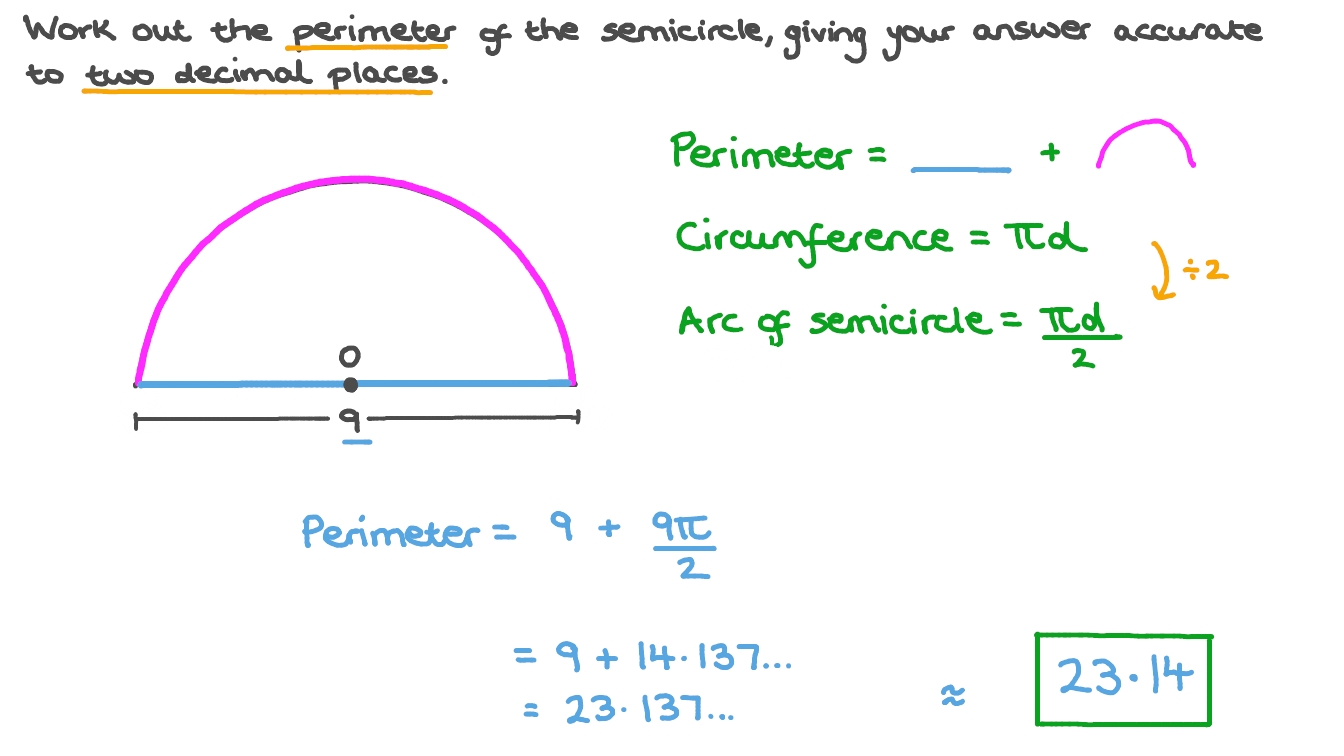
where a, b, and c are the lengths of the sides. - Circle: The perimeter of a circle, also known as the circumference, is calculated using the radius or diameter:
C = 2πrorC = πd
where r is the radius and d is the diameter.
Steps to Calculate Perimeter
- Identify the shape of the figure.
- Use the appropriate formula based on the shape.
- Measure or obtain the lengths of all the sides.
- Substitute the values into the formula.
- Perform the necessary arithmetic operations to find the perimeter.
Example Calculations
Let's calculate the perimeter for a rectangle with a length of 8 units and a width of 3 units:
- Formula:
P = 2l + 2w - Substitute the values:
P = 2(8) + 2(3) - Perform the operations:
P = 16 + 6 = 22 units
For a square with each side measuring 5 units, the calculation is straightforward:
- Formula:
P = 4s - Substitute the value:
P = 4(5) - Perform the operation:
P = 20 units
Understanding perimeter is essential for solving real-world problems, such as determining the amount of fencing required to enclose a garden or the length of trim needed for a room.

Common Shapes and Their Perimeters
The perimeter of a shape is the total distance around its edges. Here, we will explore the perimeters of some common geometric shapes and provide formulas for calculating them.
Square
The perimeter of a square is calculated by summing the lengths of all four sides.
Formula:
\( P = 4s \)
Where \( s \) is the length of one side of the square.
Rectangle
The perimeter of a rectangle is the sum of twice the length and twice the width.
Formula:
\( P = 2l + 2w \)
Where \( l \) is the length and \( w \) is the width of the rectangle.
Triangle
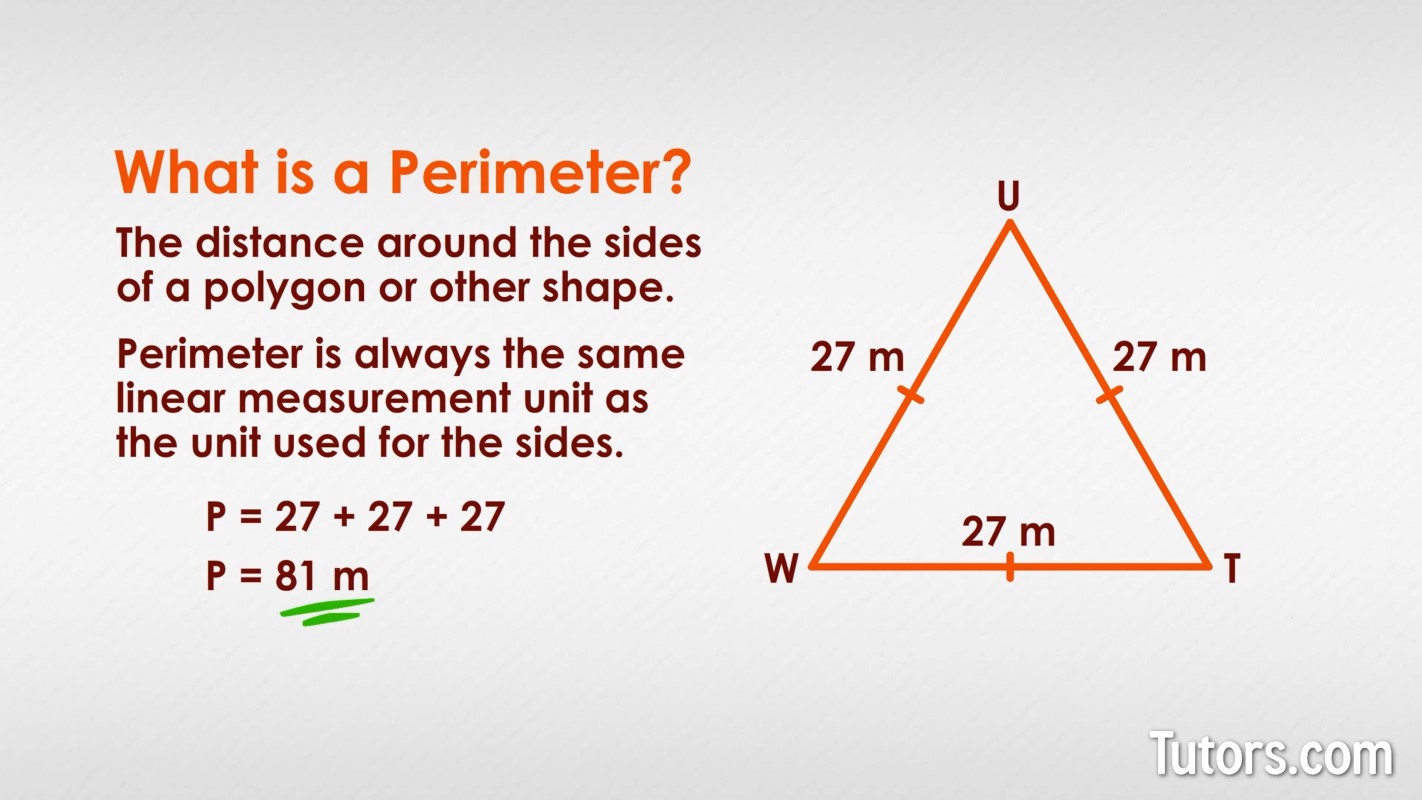
The perimeter of a triangle is the sum of the lengths of its three sides.
Formula:
\( P = a + b + c \)
Where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
Circle
The perimeter of a circle is also known as the circumference. It is calculated using the radius or diameter of the circle.
Formulas:
\( C = 2\pi r \) (using the radius)
\( C = \pi d \) (using the diameter)
Where \( r \) is the radius and \( d \) is the diameter of the circle.
Parallelogram
The perimeter of a parallelogram is the sum of the lengths of its four sides.
Formula:
\( P = 2a + 2b \)
Where \( a \) and \( b \) are the lengths of the adjacent sides of the parallelogram.
Trapezoid
The perimeter of a trapezoid is the sum of the lengths of its four sides.
Formula:
\( P = a + b + c + d \)
Where \( a \), \( b \), \( c \), and \( d \) are the lengths of the sides of the trapezoid.
Regular Polygon
The perimeter of a regular polygon (a polygon with all sides and angles equal) is the product of the number of sides and the length of one side.
Formula:
\( P = n \times s \)
Where \( n \) is the number of sides and \( s \) is the length of one side.
Understanding and calculating the perimeter is essential in various real-life applications, such as fencing a garden, framing a picture, or any scenario where determining the boundary length is necessary.
Advanced Perimeter Calculations
Advanced perimeter calculations often involve composite shapes or irregular figures. These calculations require a combination of basic geometric formulas and sometimes advanced mathematical techniques. Below are some methods and examples for advanced perimeter calculations:
Perimeter of Composite Shapes
Composite shapes are made up of two or more simple geometric shapes. To find the perimeter of a composite shape, sum the perimeters of the individual shapes, making sure to subtract any internal sides that are not part of the external boundary.
Example:
- Consider a shape made of a rectangle and a semicircle.
- First, calculate the perimeter of the rectangle: \( P_{\text{rect}} = 2(l + w) \).
- Next, calculate the perimeter of the semicircle: \( P_{\text{semi}} = \pi r + 2r \) (since the diameter forms part of the rectangle's side).
- Sum these perimeters: \( P_{\text{total}} = 2(l + w) + \pi r \).
Perimeter of Irregular Shapes
For irregular shapes, break the shape down into known geometric figures, find the perimeters of these figures, and sum them accordingly. If the shape has curves or non-linear edges, use integral calculus to approximate the perimeter.
Example:
- An irregular polygon with vertices at \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\).
- Calculate the distance between each pair of consecutive vertices using the distance formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Sum all these distances to get the total perimeter: \( P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} \).
Using Trigonometry in Perimeter Calculations
Trigonometry can help find the perimeter of shapes involving angles and lengths that are not easily measured directly.
Example:
- For a regular polygon with \( n \) sides of length \( s \), use the formula: \( P = ns \).
- For a sector of a circle with radius \( r \) and angle \( \theta \) (in radians), the perimeter is \( P = 2r + r\theta \) (the sum of the two radii and the arc length).
Real-Life Applications
Advanced perimeter calculations are crucial in various fields such as architecture, engineering, and computer graphics.
- Architecture: Calculating the boundary of a plot of land or the edges of a complex structure.
- Engineering: Determining the lengths of materials needed for construction projects.
- Computer Graphics: Rendering the outlines of complex shapes in digital models.
By mastering these advanced techniques, you can accurately calculate the perimeter of any shape, no matter how complex.
Understanding Volume
Volume is a measure of the amount of space a three-dimensional object occupies. It is quantified in cubic units. Understanding volume is essential in various fields such as engineering, architecture, and everyday tasks like packing or measuring liquids.
Here, we will explore the volume of common shapes and the methods to calculate them:
Volume of a Cube
A cube is a three-dimensional shape with six equal square faces. The formula to calculate the volume of a cube is:
\[ V = a^3 \]
where \( a \) is the length of any edge of the cube.
- Example: If a cube has an edge length of 4 cm, then its volume is \( V = 4^3 = 64 \text{ cm}^3 \).
Volume of a Rectangular Prism
A rectangular prism has six faces that are rectangles. The formula to calculate its volume is:
\[ V = l \times w \times h \]
where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- Example: For a rectangular prism with dimensions 5 cm, 3 cm, and 2 cm, the volume is \( V = 5 \times 3 \times 2 = 30 \text{ cm}^3 \).
Volume of a Cylinder
A cylinder has two parallel circular bases and a curved surface connecting them. The formula to calculate the volume of a cylinder is:
\[ V = \pi r^2 h \]
where \( r \) is the radius of the base and \( h \) is the height.
- Example: For a cylinder with a base radius of 3 cm and a height of 10 cm, the volume is \( V = \pi \times 3^2 \times 10 \approx 282.74 \text{ cm}^3 \).
Volume of a Sphere
A sphere is a perfectly round three-dimensional shape. The formula to calculate the volume of a sphere is:
\[ V = \frac{4}{3} \pi r^3 \]
where \( r \) is the radius of the sphere.
- Example: If a sphere has a radius of 6 cm, its volume is \( V = \frac{4}{3} \pi \times 6^3 \approx 904.32 \text{ cm}^3 \).
Volume of a Cone
A cone has a circular base and a pointed top. The formula to calculate the volume of a cone is:
\[ V = \frac{1}{3} \pi r^2 h \]
where \( r \) is the radius of the base and \( h \) is the height.
- Example: For a cone with a base radius of 3 cm and a height of 8 cm, the volume is \( V = \frac{1}{3} \pi \times 3^2 \times 8 \approx 75.40 \text{ cm}^3 \).
Volume of a Pyramid
A pyramid has a polygonal base and triangular faces that converge to a point. The formula to calculate the volume of a pyramid is:
\[ V = \frac{1}{3} \text{Base Area} \times h \]
where \( h \) is the height from the base to the apex.
- Example: For a pyramid with a square base of side 4 cm and a height of 9 cm, the volume is \( V = \frac{1}{3} \times 4^2 \times 9 = 48 \text{ cm}^3 \).
Practice Problems
Here are some practice problems to reinforce your understanding:
- Calculate the volume of a cube with a side length of 7 cm.
- Find the volume of a rectangular prism with dimensions 8 cm, 6 cm, and 4 cm.
- Determine the volume of a cylinder with a radius of 5 cm and a height of 12 cm.
- Calculate the volume of a sphere with a radius of 10 cm.
- Find the volume of a cone with a base radius of 4 cm and a height of 9 cm.
- Determine the volume of a pyramid with a rectangular base of 6 cm by 8 cm and a height of 10 cm.
Common Shapes and Their Volumes
Understanding the volume of common shapes is essential in various fields, including engineering, architecture, and everyday life. Here are the volume formulas for some frequently encountered 3D shapes:
- Cube
- \(s\) = side length
- Rectangular Prism
- \(l\) = length
- \(w\) = width
- \(h\) = height
- Cylinder
- \(r\) = radius of the base
- \(h\) = height
- Sphere
- \(r\) = radius
- Cone
- \(r\) = radius of the base
- \(h\) = height
- Square Pyramid
- \(b\) = side length of the base
- \(h\) = height
- Triangular Prism
- \(b\) = base length of the triangle
- \(h\) = height of the triangle
- \(l\) = length of the prism
A cube has all sides of equal length.
Volume: \( V = s^3 \)
A rectangular prism has three pairs of parallel faces.
Volume: \( V = l \times w \times h \)
A cylinder has two parallel circular bases connected by a curved surface.
Volume: \( V = \pi r^2 h \)
A sphere is a perfectly round 3D shape.
Volume: \( V = \frac{4}{3} \pi r^3 \)
A cone has a circular base and a pointed top.
Volume: \( V = \frac{1}{3} \pi r^2 h \)
A square pyramid has a square base and four triangular faces that meet at a point.
Volume: \( V = \frac{1}{3} b^2 h \)
A triangular prism has two parallel triangular bases connected by three rectangular faces.
Volume: \( V = \frac{1}{2} b h l \)
Advanced Volume Calculations
Advanced volume calculations involve understanding and applying the formulas for various three-dimensional shapes. These calculations are essential in fields such as engineering, architecture, and science.
Volume of a Rectangular Prism
The volume \( V \) of a rectangular prism (or cuboid) is calculated by multiplying the length \( l \), width \( w \), and height \( h \) of the prism:
\[
V = l \times w \times h
\]
For example, a rectangular prism with dimensions \( l = 5 \, \text{m} \), \( w = 3 \, \text{m} \), and \( h = 4 \, \text{m} \) has a volume of:
\[
V = 5 \, \text{m} \times 3 \, \text{m} \times 4 \, \text{m} = 60 \, \text{m}^3
\]
Volume of a Cylinder
The volume \( V \) of a cylinder is found by multiplying the area of its base (a circle) by its height \( h \):
\[
V = \pi r^2 h
\]
Where \( r \) is the radius of the base. For a cylinder with \( r = 2 \, \text{m} \) and \( h = 10 \, \text{m} \), the volume is:
\[
V = \pi (2 \, \text{m})^2 \times 10 \, \text{m} = 40\pi \, \text{m}^3 \approx 125.66 \, \text{m}^3
\]
Volume of a Sphere
The volume \( V \) of a sphere is calculated using the formula:
\[
V = \frac{4}{3} \pi r^3
\]
Where \( r \) is the radius. For a sphere with a radius of \( r = 3 \, \text{m} \), the volume is:
\[
V = \frac{4}{3} \pi (3 \, \text{m})^3 = \frac{4}{3} \pi \times 27 \, \text{m}^3 = 36\pi \, \text{m}^3 \approx 113.10 \, \text{m}^3
\]
Volume of a Cone
The volume \( V \) of a cone is found by multiplying the area of the base (a circle) by the height \( h \), then dividing by 3:
\[
V = \frac{1}{3} \pi r^2 h
\]
For a cone with \( r = 2 \, \text{m} \) and \( h = 5 \, \text{m} \), the volume is:
\[
V = \frac{1}{3} \pi (2 \, \text{m})^2 \times 5 \, \text{m} = \frac{1}{3} \pi \times 20 \, \text{m}^3 = \frac{20\pi}{3} \, \text{m}^3 \approx 20.94 \, \text{m}^3
\]
Composite Shapes
For composite shapes, divide the shape into simpler components, calculate the volume for each component, and then sum these volumes. For example, to find the volume of a shape consisting of a cylinder on top of a rectangular prism:
- Calculate the volume of the rectangular prism.
- Calculate the volume of the cylinder.
- Add the two volumes together.
Practice Problems
- Find the volume of a rectangular prism with \( l = 6 \, \text{m} \), \( w = 4 \, \text{m} \), and \( h = 5 \, \text{m} \).
- Calculate the volume of a cylinder with a radius of \( 3 \, \text{m} \) and height of \( 7 \, \text{m} \).
- Determine the volume of a sphere with a radius of \( 4 \, \text{m} \).
- Find the volume of a cone with \( r = 2.5 \, \text{m} \) and \( h = 6 \, \text{m} \).
- Calculate the total volume of a shape that consists of a cone (base radius \( 2 \, \text{m} \), height \( 3 \, \text{m} \)) sitting on top of a cylinder (radius \( 2 \, \text{m} \), height \( 4 \, \text{m} \)).
Area Practice Problems
Here are some practice problems to help you master the concept of area. Solve these problems step by step, and use the provided hints if needed.
Problem 1: Rectangular Garden
You have a rectangular garden that is 8 meters long and 5 meters wide. Calculate the area of the garden.
- Write down the formula for the area of a rectangle: \( \text{Area} = \text{length} \times \text{width} \)
- Substitute the given values into the formula: \( \text{Area} = 8 \, \text{m} \times 5 \, \text{m} \)
- Calculate the result: \( \text{Area} = 40 \, \text{m}^2 \)
Answer: The area of the garden is 40 square meters.
Problem 2: Circular Field
A circular field has a radius of 7 meters. Find the area of the field. Use \( \pi \approx 3.14 \).
- Write down the formula for the area of a circle: \( \text{Area} = \pi \times \text{radius}^2 \)
- Substitute the given values into the formula: \( \text{Area} = 3.14 \times 7^2 \)
- Calculate the result: \( \text{Area} = 3.14 \times 49 \)
- Finish the calculation: \( \text{Area} = 153.86 \, \text{m}^2 \)
Answer: The area of the circular field is approximately 153.86 square meters.
Problem 3: Triangular Plot
A triangular plot of land has a base of 10 meters and a height of 6 meters. Determine the area of the plot.
- Write down the formula for the area of a triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Substitute the given values into the formula: \( \text{Area} = \frac{1}{2} \times 10 \, \text{m} \times 6 \, \text{m} \)
- Calculate the result: \( \text{Area} = \frac{1}{2} \times 60 \, \text{m}^2 \)
- Finish the calculation: \( \text{Area} = 30 \, \text{m}^2 \)
Answer: The area of the triangular plot is 30 square meters.
Problem 4: Composite Shape
A composite shape is made up of a rectangle and a semicircle. The rectangle is 12 meters long and 4 meters wide, and the semicircle has a diameter of 4 meters. Calculate the total area of the shape.
- Calculate the area of the rectangle: \( \text{Area}_{\text{rectangle}} = 12 \, \text{m} \times 4 \, \text{m} = 48 \, \text{m}^2 \)
- Calculate the radius of the semicircle: \( \text{radius} = \frac{\text{diameter}}{2} = \frac{4 \, \text{m}}{2} = 2 \, \text{m} \)
- Calculate the area of the semicircle: \( \text{Area}_{\text{semicircle}} = \frac{1}{2} \times \pi \times \text{radius}^2 = \frac{1}{2} \times 3.14 \times 2^2 = \frac{1}{2} \times 3.14 \times 4 = 6.28 \, \text{m}^2 \)
- Add the areas together: \( \text{Total Area} = \text{Area}_{\text{rectangle}} + \text{Area}_{\text{semicircle}} = 48 \, \text{m}^2 + 6.28 \, \text{m}^2 = 54.28 \, \text{m}^2 \)
Answer: The total area of the composite shape is 54.28 square meters.
Problem 5: Parallelogram Floor
A parallelogram-shaped floor has a base of 15 meters and a height of 8 meters. Find the area of the floor.
- Write down the formula for the area of a parallelogram: \( \text{Area} = \text{base} \times \text{height} \)
- Substitute the given values into the formula: \( \text{Area} = 15 \, \text{m} \times 8 \, \text{m} \)
- Calculate the result: \( \text{Area} = 120 \, \text{m}^2 \)
Answer: The area of the parallelogram floor is 120 square meters.
Practice these problems to enhance your understanding of calculating areas for different shapes. You can also create similar problems to further strengthen your skills.
Perimeter Practice Problems
Here are some practice problems to help you master calculating the perimeter of various shapes:
-
Problem 1: Find the perimeter of a rectangle with a length of 12 cm and a width of 8 cm.
Solution: The formula for the perimeter of a rectangle is \( P = 2 \times (l + w) \).
\[ P = 2 \times (12 \, \text{cm} + 8 \, \text{cm}) = 2 \times 20 \, \text{cm} = 40 \, \text{cm} \]
-
Problem 2: A triangle has sides measuring 5 m, 7 m, and 9 m. Find its perimeter.
Solution: The perimeter of a triangle is the sum of its sides.
\[ P = 5 \, \text{m} + 7 \, \text{m} + 9 \, \text{m} = 21 \, \text{m} \]
-
Problem 3: Calculate the perimeter of a square where each side is 6 inches.
Solution: The perimeter of a square is four times the length of one side.
\[ P = 4 \times 6 \, \text{in} = 24 \, \text{in} \]
-
Problem 4: A regular hexagon has each side measuring 10 cm. Find its perimeter.
Solution: The perimeter of a regular hexagon is six times the length of one side.
\[ P = 6 \times 10 \, \text{cm} = 60 \, \text{cm} \]
-
Problem 5: A rectangle has a perimeter of 50 cm. If its length is 15 cm, what is its width?
Solution: Use the formula for the perimeter of a rectangle \( P = 2 \times (l + w) \) and solve for \( w \).
\[ 50 \, \text{cm} = 2 \times (15 \, \text{cm} + w) \]
\[ 25 \, \text{cm} = 15 \, \text{cm} + w \]
\[ w = 10 \, \text{cm} \]
-
Problem 6: Find the perimeter of a trapezoid with bases of 8 cm and 6 cm, and non-parallel sides of 5 cm each.
Solution: The perimeter of a trapezoid is the sum of all its sides.
\[ P = 8 \, \text{cm} + 6 \, \text{cm} + 5 \, \text{cm} + 5 \, \text{cm} = 24 \, \text{cm} \]
-
Problem 7: Calculate the perimeter of an equilateral triangle with each side measuring 9 inches.
Solution: The perimeter of an equilateral triangle is three times the length of one side.
\[ P = 3 \times 9 \, \text{in} = 27 \, \text{in} \]
Volume Practice Problems
Practice solving the following volume problems. Each problem requires you to find the volume of different three-dimensional shapes.
Problem 1: Rectangular Prism
A rectangular prism has a length of 5 cm, a width of 3 cm, and a height of 4 cm. Calculate its volume.
- Formula: \( V = l \times w \times h \)
- Solution:
- \( l = 5 \) cm
- \( w = 3 \) cm
- \( h = 4 \) cm
- \( V = 5 \times 3 \times 4 = 60 \) cubic cm
Problem 2: Sphere
A sphere has a diameter of 10 cm. Calculate its volume. Use \( \pi \approx 3.1416 \).
- Formula: \( V = \frac{4}{3}\pi r^3 \)
- Solution:
- Radius \( r = \frac{10}{2} = 5 \) cm
- \( V = \frac{4}{3} \times 3.1416 \times 5^3 \)
- \( V = \frac{4}{3} \times 3.1416 \times 125 \)
- \( V \approx 523.6 \) cubic cm
Problem 3: Cylinder
A cylinder has a radius of 7 cm and a height of 10 cm. Calculate its volume. Use \( \pi \approx 3.1416 \).
- Formula: \( V = \pi r^2 h \)
- Solution:
- Radius \( r = 7 \) cm
- Height \( h = 10 \) cm
- \( V = 3.1416 \times 7^2 \times 10 \)
- \( V = 3.1416 \times 49 \times 10 \)
- \( V \approx 1539.38 \) cubic cm
Problem 4: Cone
A cone has a radius of 4 cm and a height of 9 cm. Calculate its volume. Use \( \pi \approx 3.1416 \).
- Formula: \( V = \frac{1}{3}\pi r^2 h \)
- Solution:
- Radius \( r = 4 \) cm
- Height \( h = 9 \) cm
- \( V = \frac{1}{3} \times 3.1416 \times 4^2 \times 9 \)
- \( V = \frac{1}{3} \times 3.1416 \times 16 \times 9 \)
- \( V \approx 150.8 \) cubic cm
Problem 5: Composite Shape
A composite shape consists of a cylinder with a radius of 6 cm and a height of 8 cm, and a hemisphere on top with the same radius. Calculate the total volume. Use \( \pi \approx 3.1416 \).
- Formula:
- Cylinder: \( V = \pi r^2 h \)
- Hemisphere: \( V = \frac{2}{3}\pi r^3 \)
- Solution:
- Radius \( r = 6 \) cm
- Height \( h = 8 \) cm
- Cylinder Volume: \( V = 3.1416 \times 6^2 \times 8 \)
- Cylinder Volume: \( V = 3.1416 \times 36 \times 8 \)
- Cylinder Volume: \( V \approx 904.32 \) cubic cm
- Hemisphere Volume: \( V = \frac{2}{3} \times 3.1416 \times 6^3 \)
- Hemisphere Volume: \( V = \frac{2}{3} \times 3.1416 \times 216 \)
- Hemisphere Volume: \( V \approx 452.39 \) cubic cm
- Total Volume: \( V_{total} = 904.32 + 452.39 = 1356.71 \) cubic cm

Summary and Review
In this guide, we have covered the fundamental concepts of area, perimeter, and volume. Let's summarize the key points and review the essential formulas and applications discussed.
Area
- Definition: The amount of space inside the boundary of a flat object or surface.
- Common Formulas:
- Rectangle: \( A = l \times w \)
- Triangle: \( A = \frac{1}{2} \times b \times h \)
- Circle: \( A = \pi r^2 \)
- Applications: Calculating the area is essential in fields such as architecture, agriculture, and interior design to determine the amount of material needed or the usable space.
Perimeter
- Definition: The distance around the boundary of a flat object.
- Common Formulas:
- Rectangle: \( P = 2(l + w) \)
- Triangle: \( P = a + b + c \)
- Circle (Circumference): \( P = 2\pi r \)
- Applications: Perimeter calculations are used in fencing, framing, and any project requiring the measurement of the boundary length of a shape.
Volume
- Definition: The amount of space inside a three-dimensional object.
- Common Formulas:
- Rectangular Prism: \( V = l \times w \times h \)
- Cylinder: \( V = \pi r^2 h \)
- Sphere: \( V = \frac{4}{3} \pi r^3 \)
- Applications: Volume calculations are critical in manufacturing, packaging, and construction to determine capacity and material usage.
Key Takeaways
- Understanding and using the formulas for area, perimeter, and volume are fundamental skills in geometry.
- These measurements are applied in various real-world contexts, from simple tasks like wrapping a gift to complex architectural design.
- Practicing these calculations with different shapes enhances problem-solving skills and spatial reasoning.
Practice Problems
For further practice, revisit the practice problems provided for each section:
Final Thoughts
Mastering these geometric concepts lays a strong foundation for more advanced mathematical studies and practical applications. Keep practicing, and apply these principles to everyday problems to enhance your understanding and proficiency.
Giải thích chu vi, diện tích, và thể tích một cách dễ hiểu với Thầy J. Tìm hiểu về các khái niệm toán học cơ bản này qua video.
Giải Thích Chu Vi, Diện Tích, và Thể Tích | Toán với Thầy J
READ MORE:
Video Toán Học Vui Nhộn giải thích về thể tích. Tìm hiểu cách tính thể tích các hình học với phương pháp dễ hiểu và thú vị.
Toán Học Vui Nhộn - Thể Tích