Topic area of perimeter of triangle: This comprehensive guide delves into the fascinating world of triangle geometry, covering essential concepts, definitions, and formulas for calculating the area and perimeter of various types of triangles. Whether you're a student, teacher, or math enthusiast, this article will provide you with practical examples and a solid understanding of triangle geometry.
Table of Content
- Area and Perimeter of a Triangle
- Introduction to Triangle Geometry
- Basic Definitions
- Formulas for Area of a Triangle
- Heron's Formula
- Area Using Base and Height
- Area Using Two Sides and the Included Angle
- Area of Equilateral Triangle
- Area of Isosceles Triangle
- Practical Examples for Calculating Area
- Formulas for Perimeter of a Triangle
- Perimeter of Equilateral Triangle
- Perimeter of Isosceles Triangle
- Units of Measurement for Area and Perimeter
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách tìm diện tích và chu vi của tam giác với Thầy J. Video này sẽ giúp bạn hiểu rõ hơn về các công thức và phương pháp tính toán trong hình học.
Area and Perimeter of a Triangle
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its three sides. For a triangle with sides of lengths \(a\), \(b\), and \(c\), the formula is:
\(\text{Perimeter} = a + b + c\)
Example: If a triangle has sides of lengths 5 cm, 7 cm, and 10 cm, the perimeter is:
\(\text{Perimeter} = 5 + 7 + 10 = 22 \, \text{cm}\)
Area of a Triangle
The area of a triangle can be calculated using various formulas depending on the given dimensions.
Using Base and Height
If the base \(b\) and height \(h\) of the triangle are known, the area is given by:
\(\text{Area} = \frac{1}{2} \times b \times h\)
Example: For a triangle with a base of 8 cm and a height of 5 cm:
\(\text{Area} = \frac{1}{2} \times 8 \times 5 = 20 \, \text{cm}^2\)
Using Heron's Formula
When the lengths of all three sides are known, Heron's formula can be used. Let \(a\), \(b\), and \(c\) be the sides of the triangle, and \(s\) be the semi-perimeter \(\left( s = \frac{a + b + c}{2} \right)\). The area is:
\(\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}\)
Example: For a triangle with sides of lengths 5 cm, 12 cm, and 13 cm:
\(s = \frac{5 + 12 + 13}{2} = 15\)
\(\text{Area} = \sqrt{15(15 - 5)(15 - 12)(15 - 13)} = \sqrt{15 \times 10 \times 3 \times 2} = \sqrt{900} = 30 \, \text{cm}^2\)
Using Two Sides and the Included Angle
If two sides and the included angle are known, the area can be found using the formula:
\(\text{Area} = \frac{1}{2} \times a \times b \times \sin(C)\)
Example: For a triangle with sides 7 cm and 10 cm, and an included angle of 45°:
\(\text{Area} = \frac{1}{2} \times 7 \times 10 \times \sin(45^\circ) = \frac{1}{2} \times 7 \times 10 \times \frac{\sqrt{2}}{2} = 24.75 \, \text{cm}^2\)
Special Triangles
- Equilateral Triangle: The area can be calculated using the formula: \(\text{Area} = \frac{\sqrt{3}}{4} \times a^2\), where \(a\) is the side length.
- Isosceles Triangle: If the base \(b\) and the equal sides \(a\) are known, the area is: \(\text{Area} = \frac{1}{4} \times b \times \sqrt{4a^2 - b^2}\).

READ MORE:
Introduction to Triangle Geometry
The study of triangles, one of the most fundamental shapes in geometry, involves understanding both their area and perimeter. Triangles are used extensively in various fields such as architecture, engineering, and art due to their structural stability and aesthetic appeal. A triangle is a three-sided polygon with three angles. The sum of the interior angles of any triangle is always 180 degrees.
To better understand triangle geometry, it's essential to grasp two key concepts: area and perimeter. The area of a triangle measures the region enclosed by its three sides, while the perimeter is the total distance around the triangle. These properties are crucial for solving real-world problems, from calculating land areas to designing buildings.
- Area: The area of a triangle can be calculated using various methods, such as Heron's formula, the base-height method, and trigonometric formulas for specific types of triangles.
- Perimeter: The perimeter is simply the sum of the lengths of all three sides. For an equilateral triangle, the formula is \( P = 3a \), where \( a \) is the length of a side.
Understanding these concepts not only enhances problem-solving skills but also provides a solid foundation for advanced studies in mathematics and its applications in the real world.
Basic Definitions
Understanding the area and perimeter of a triangle involves some fundamental definitions:
- Triangle: A three-sided polygon formed by three line segments.
- Vertices: The points where the sides of a triangle meet.
- Base: Any one of the triangle's sides can be considered the base.
- Height: The perpendicular distance from the base to the opposite vertex.
- Sides: The lengths of the edges of the triangle.
- Angles: The space between two intersecting lines at each vertex, with the sum of the interior angles always equal to \(180^\circ\).
In terms of measurements:
- Area: The space enclosed within the triangle, measured in square units. The formula is \( \text{Area} = \frac{1}{2} \times \text{Base} \times \text{Height} \).
- Perimeter: The total distance around the triangle, calculated by adding the lengths of all three sides. The formula is \( \text{Perimeter} = a + b + c \).
These basic definitions are essential for calculating the area and perimeter of various types of triangles, such as equilateral, isosceles, and scalene triangles.
Formulas for Area of a Triangle
The area of a triangle can be calculated using various formulas depending on the known dimensions. Here are the most commonly used formulas:
- When the base and height of a triangle are given:
- Formula: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Example: If the base is 8 cm and the height is 5 cm, then \( A = \frac{1}{2} \times 8 \times 5 = 20 \, \text{cm}^2 \).
- Using Heron's formula when all three sides are known:
- Formula: \( A = \sqrt{s(s-a)(s-b)(s-c)} \), where \( s = \frac{a+b+c}{2} \)
- Example: For sides of lengths 5 cm, 6 cm, and 7 cm, first calculate \( s = \frac{5+6+7}{2} = 9 \). Then \( A = \sqrt{9(9-5)(9-6)(9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \, \text{cm}^2 \).
- When two sides and the included angle are given:
- Formula: \( A = \frac{1}{2} \times a \times b \times \sin(C) \)
- Example: If \( a = 7 \, \text{cm} \), \( b = 10 \, \text{cm} \), and \( C = 30^\circ \), then \( A = \frac{1}{2} \times 7 \times 10 \times \sin(30^\circ) = 35 \, \text{cm}^2 \).
- For an equilateral triangle:
- Formula: \( A = \frac{\sqrt{3}}{4} \times a^2 \)
- Example: If each side is 4 cm, then \( A = \frac{\sqrt{3}}{4} \times 4^2 = 4 \sqrt{3} \approx 6.93 \, \text{cm}^2 \).
- For an isosceles triangle:
- Formula: \( A = \frac{1}{4} \times b \sqrt{4a^2 - b^2} \), where \( a \) is the length of the equal sides and \( b \) is the base.
- Example: If \( a = 5 \, \text{cm} \) and \( b = 6 \, \text{cm} \), then \( A = \frac{1}{4} \times 6 \sqrt{4 \times 5^2 - 6^2} = 12 \, \text{cm}^2 \).
Heron's Formula
Heron's formula is a powerful tool for calculating the area of a triangle when you know the lengths of all three sides. Unlike other methods, it doesn't require the height of the triangle, making it very versatile.
To use Heron's formula, follow these steps:
- Calculate the semi-perimeter \(s\) of the triangle: \[ s = \frac{a + b + c}{2} \] where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
- Substitute the values of \(a\), \(b\), \(c\), and \(s\) into Heron's formula to find the area \(A\): \[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
Let's consider an example to illustrate the use of Heron's formula:
- Given a triangle with side lengths \(a = 5\), \(b = 12\), and \(c = 13\):
- First, calculate the semi-perimeter \(s\): \[ s = \frac{5 + 12 + 13}{2} = 15 \]
- Next, use the semi-perimeter in Heron's formula: \[ A = \sqrt{15(15 - 5)(15 - 12)(15 - 13)} = \sqrt{15 \cdot 10 \cdot 3 \cdot 2} = \sqrt{900} = 30 \]
Therefore, the area of the triangle is 30 square units.
Heron's formula can be applied to any triangle as long as the side lengths are known, providing a reliable method for area calculation without needing height measurements.
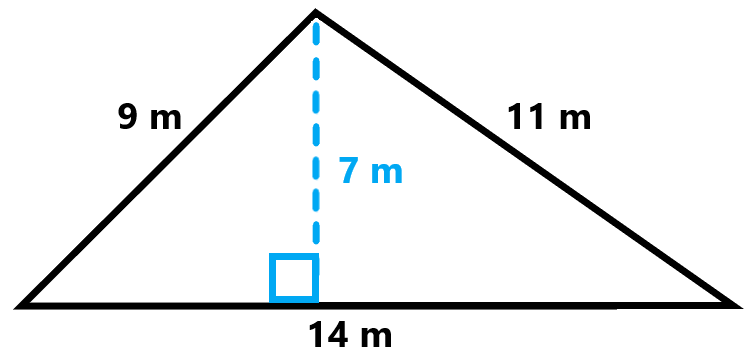
Area Using Base and Height
The area of a triangle can be calculated if the length of the base and the height are known. The formula for the area is derived from the fact that a triangle can be thought of as half of a parallelogram.
The formula to find the area \( A \) of a triangle using its base \( b \) and height \( h \) is:
\[ A = \frac{1}{2} \times b \times h \]
Where:
- \( b \) is the length of the base of the triangle.
- \( h \) is the height of the triangle, which is the perpendicular distance from the base to the opposite vertex.
Here is a step-by-step method to use this formula:
- Identify the base (\( b \)) of the triangle. This can be any one of the three sides, but it is usually the one on the bottom when the triangle is drawn.
- Determine the height (\( h \)) of the triangle. This is the perpendicular distance from the base to the top vertex (opposite the base).
- Multiply the base by the height.
- Divide the result by 2 to get the area of the triangle.
For example, if the base of a triangle is 5 cm and the height is 8 cm, the area is calculated as follows:
\[ A = \frac{1}{2} \times 5 \, \text{cm} \times 8 \, \text{cm} = \frac{1}{2} \times 40 \, \text{cm}^2 = 20 \, \text{cm}^2 \]
This method is applicable to all types of triangles as long as the base and height are known.
Area Using Two Sides and the Included Angle
The area of a triangle can also be calculated if you know the lengths of two sides and the measure of the included angle between them. This method is particularly useful when the height of the triangle is not readily available. The formula to find the area of such a triangle is derived from trigonometry and is given by:
\[ A = \frac{1}{2}ab \sin(C) \]
Here:
- a and b are the lengths of the two sides.
- C is the measure of the included angle between sides a and b.
Let's break down the steps to calculate the area:
- Measure the lengths of the two sides: Identify and measure the lengths of the two sides, a and b.
- Determine the included angle: Measure the angle C between the two sides.
- Apply the formula: Substitute the values of a, b, and C into the formula and compute the area.
Example Calculation:
- Suppose we have a triangle with sides a = 5 cm and b = 7 cm, and the included angle C = 60°.
- Using the formula: \[ A = \frac{1}{2} \times 5 \times 7 \times \sin(60^\circ) \]
- We know that \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\).
- So, \[ A = \frac{1}{2} \times 5 \times 7 \times \frac{\sqrt{3}}{2} = \frac{35 \sqrt{3}}{4} \approx 15.14 \text{ cm}^2 \]
Therefore, the area of the triangle is approximately \(15.14 \text{ cm}^2\).
This formula is very flexible and can be used for any triangle where two sides and the included angle are known, making it a powerful tool in geometry.
Area of Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are of equal length and all internal angles are equal to 60 degrees. The formula to calculate the area of an equilateral triangle is derived from its unique properties.
Formula for Area
The area \( A \) of an equilateral triangle with side length \( a \) can be calculated using the formula:
Derivation
The derivation of the area formula involves using the Pythagorean theorem to find the height of the triangle. Consider an equilateral triangle with side length \( a \). Dropping a perpendicular from one vertex to the opposite side divides the triangle into two 30-60-90 right triangles.
In a 30-60-90 triangle, the length of the height \( h \) can be expressed as:
Using the formula for the area of a triangle \( A = \frac{1}{2} \times \text{base} \times \text{height} \), we can substitute the base \( a \) and height \( \frac{\sqrt{3}a}{2} \):
Example Calculation
Let's calculate the area of an equilateral triangle with a side length of 6 units.
Using the formula:
Thus, the area of the equilateral triangle is \( 9\sqrt{3} \) square units.
Area of Isosceles Triangle
An isosceles triangle is a triangle with two sides of equal length and two equal angles opposite those sides. The area of an isosceles triangle can be calculated using several methods depending on the given parameters.
Using Base and Height
The most common formula to find the area of an isosceles triangle is using its base and height:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Where:
- \(\text{base}\) is the length of the base of the triangle
- \(\text{height}\) is the perpendicular height from the base to the opposite vertex
Example:
Find the area of an isosceles triangle with a base of 10 cm and a height of 17 cm.
Solution:
\[ \text{Area} = \frac{1}{2} \times 10 \, \text{cm} \times 17 \, \text{cm} = 85 \, \text{cm}^2 \]
Using All Sides
If the lengths of all three sides are known, the area can be calculated using the formula:
\[ \text{Area} = \frac{1}{4} \times \sqrt{4a^2 - b^2} \times b \]
Where:
- \(a\) is the length of the two equal sides
- \(b\) is the length of the base
Example:
Find the area of an isosceles triangle with equal sides of 13 cm and a base of 10 cm.
Solution:
\[ \text{Area} = \frac{1}{4} \times \sqrt{4 \times 13^2 - 10^2} \times 10 \]
\[ = \frac{1}{4} \times \sqrt{4 \times 169 - 100} \times 10 \]
\[ = \frac{1}{4} \times \sqrt{676} \times 10 \]
\[ = \frac{1}{4} \times 26 \times 10 \]
\[ = 65 \, \text{cm}^2 \]
Using Two Sides and the Included Angle
If the lengths of two sides and the included angle are known, the area can be calculated as:
\[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\theta) \]
Where:
- \(a\) and \(b\) are the lengths of the two sides
- \(\theta\) is the included angle between the two sides
Example:
Find the area of an isosceles triangle with sides of 13 cm, 13 cm, and an included angle of 45 degrees.
Solution:
\[ \text{Area} = \frac{1}{2} \times 13 \, \text{cm} \times 13 \, \text{cm} \times \sin(45^\circ) \]
\[ = \frac{1}{2} \times 169 \times \frac{\sqrt{2}}{2} \]
\[ = 84.5 \times 0.707 \]
\[ = 59.8 \, \text{cm}^2 \]
Using Only the Length of Equal Sides
For a right isosceles triangle, where the two equal sides include the right angle, the area is:
\[ \text{Area} = \frac{1}{2} \times a^2 \]
Where:
- \(a\) is the length of the equal sides
Example:
Find the area of an isosceles right triangle with equal sides of 5 cm.
Solution:
\[ \text{Area} = \frac{1}{2} \times 5^2 \]
\[ = \frac{1}{2} \times 25 \]
\[ = 12.5 \, \text{cm}^2 \]
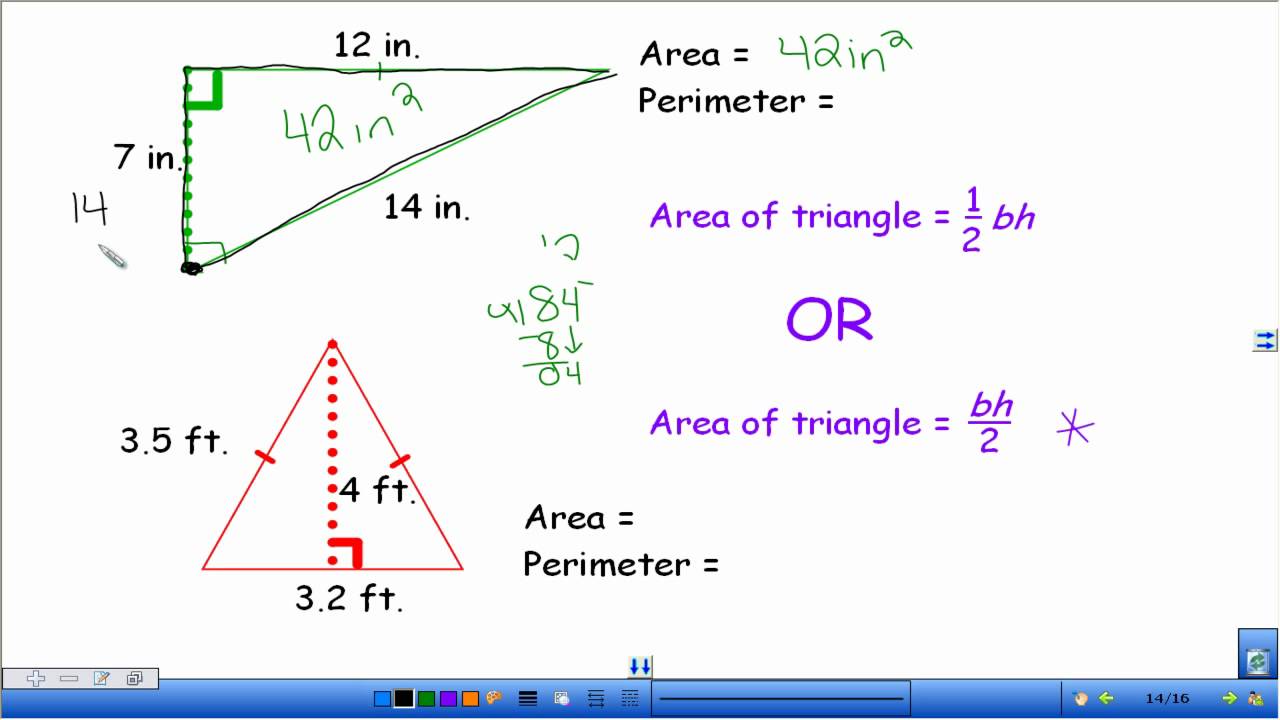
Practical Examples for Calculating Area
Here are some practical examples to help you understand how to calculate the area of different types of triangles:
Example 1: Right-Angled Triangle
Calculate the area of a right-angled triangle with a base of 3.2 cm and a height of 5.3 cm.
- Identify the base (\(b = 3.2 \, \text{cm}\)) and height (\(h = 5.3 \, \text{cm}\)).
- Use the area formula: \[A = \frac{1}{2} b h\]
- Substitute the values: \[A = \frac{1}{2} (3.2)(5.3) = 8.48 \, \text{cm}^2\]
Example 2: Obtuse Triangle
Calculate the area of an obtuse triangle with a base of 12 cm and a height of 9 cm.
- Identify the base (\(b = 12 \, \text{cm}\)) and height (\(h = 9 \, \text{cm}\)).
- Use the area formula: \[A = \frac{1}{2} b h\]
- Substitute the values: \[A = \frac{1}{2} (12)(9) = 54 \, \text{cm}^2\]
Example 3: Triangle with Mixed Units
Calculate the area of a triangle with a base of 2.5 feet and a height of 12 inches. Express the area in both square feet and square inches.
- Convert the height from inches to feet: \[12 \, \text{inches} = 1 \, \text{foot}\]
- Now, base (\(b = 2.5 \, \text{ft}\)) and height (\(h = 1 \, \text{ft}\)).
- Use the area formula: \[A = \frac{1}{2} b h\]
- Substitute the values: \[A = \frac{1}{2} (2.5)(1) = 1.25 \, \text{ft}^2\]
- Convert the base to inches: \[2.5 \, \text{ft} = 30 \, \text{in}\]
- Use the area formula: \[A = \frac{1}{2} b h\]
- Substitute the values: \[A = \frac{1}{2} (30)(12) = 180 \, \text{in}^2\]
Example 4: Given Area, Find Height
Find the height of a triangle with a base of 17 meters and an area of 204 square meters.
- Use the area formula and solve for height (\(h\)): \[A = \frac{1}{2} b h\] \[204 = \frac{1}{2} (17) h\]
- Rearrange the equation to solve for \(h\): \[h = \frac{204 \times 2}{17} = 24 \, \text{m}\]
Example 5: Base is Twice the Height
The base of a triangle is twice its height. If the area is 289 square kilometers, find the base and height.
- Let the height be \(h\) and the base be \(2h\).
- Use the area formula: \[289 = \frac{1}{2} (2h) h\] \[289 = h^2\]
- Solve for \(h\): \[h = \sqrt{289} = 17 \, \text{km}\]
- Find the base: \[2h = 2 \times 17 = 34 \, \text{km}\]
Formulas for Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle, which can be calculated by summing the lengths of all three sides. The general formula for the perimeter of a triangle is:
\[
\text{Perimeter} = a + b + c
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Perimeter of Special Triangles
- Equilateral Triangle: All sides are equal, so the perimeter can be calculated by multiplying the length of one side by 3. \[ \text{Perimeter} = 3s \] where \(s\) is the length of a side.
- Isosceles Triangle: Has two equal sides. The perimeter is calculated by adding twice the length of the equal sides and the length of the base. \[ \text{Perimeter} = 2l + b \] where \(l\) is the length of the equal sides and \(b\) is the base.
- Scalene Triangle: All sides are of different lengths. The perimeter is simply the sum of all three side lengths. \[ \text{Perimeter} = a + b + c \]
- Right Triangle: The perimeter is the sum of the base, height, and hypotenuse. \[ \text{Perimeter} = a + b + h \] where \(a\) and \(b\) are the legs, and \(h\) is the hypotenuse, which can be found using the Pythagorean theorem.
Examples
- Equilateral Triangle:
Given a side length of 5 cm, the perimeter is:
\[
\text{Perimeter} = 3 \times 5 = 15 \text{ cm}
\] - Isosceles Triangle:
Given equal side lengths of 7 cm and a base of 10 cm, the perimeter is:
\[
\text{Perimeter} = 2 \times 7 + 10 = 24 \text{ cm}
\] - Scalene Triangle:
Given side lengths of 6 cm, 8 cm, and 10 cm, the perimeter is:
\[
\text{Perimeter} = 6 + 8 + 10 = 24 \text{ cm}
\] - Right Triangle:
Given legs of 3 cm and 4 cm, and a hypotenuse of 5 cm (from the Pythagorean theorem), the perimeter is:
\[
\text{Perimeter} = 3 + 4 + 5 = 12 \text{ cm}
\]
These formulas and examples illustrate how to calculate the perimeter of various types of triangles, providing a solid foundation for understanding and applying these concepts in different scenarios.
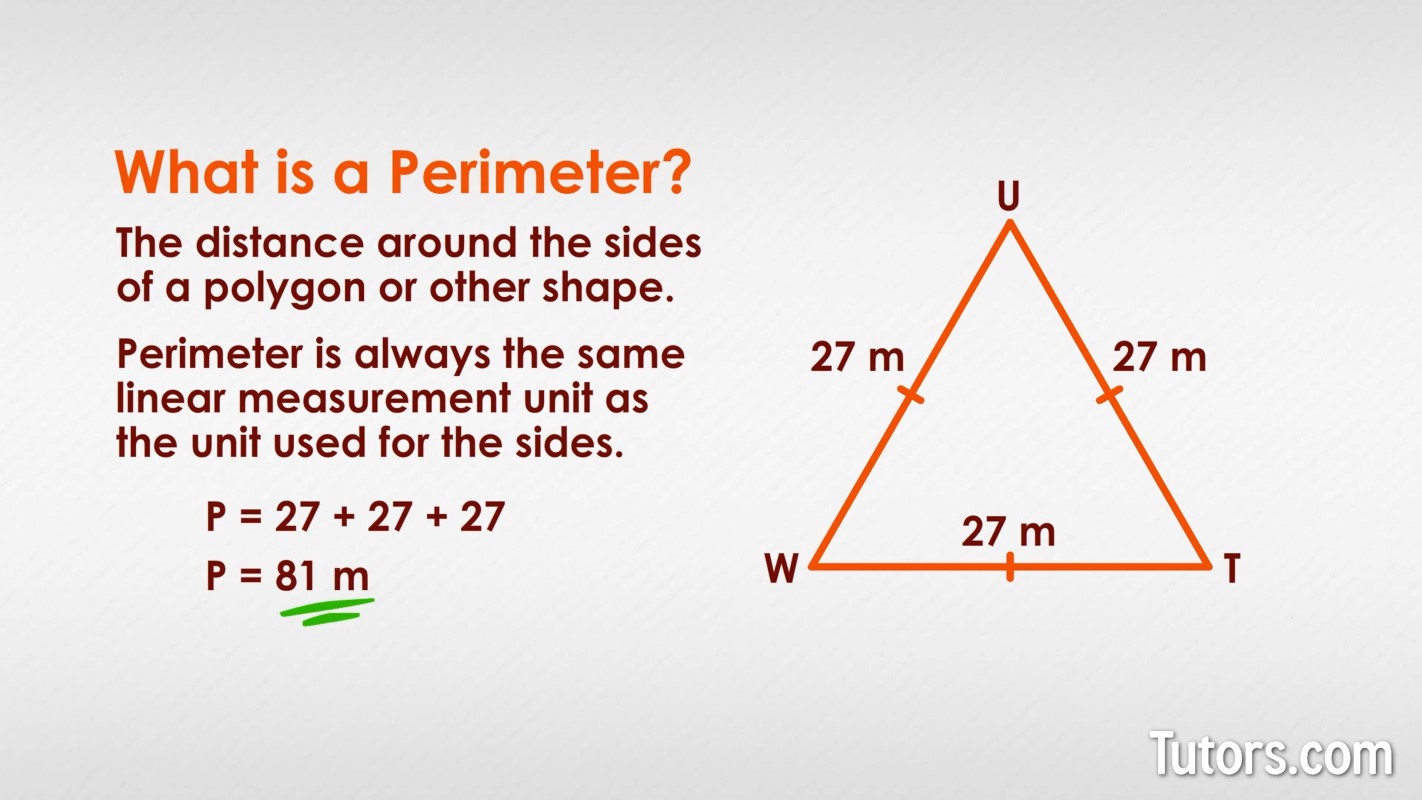
Perimeter of Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are equal in length, and all three interior angles are equal, each measuring 60 degrees. The perimeter of an equilateral triangle is calculated by summing the lengths of all its sides.
Given the side length of an equilateral triangle as \(a\), the formula to calculate the perimeter \(P\) is straightforward:
- \( P = a + a + a \)
- \( P = 3a \)
Let's consider some practical examples to understand this better:
Example 1
Calculate the perimeter of an equilateral triangle with each side measuring 5 cm.
Solution:
- Given side length, \(a = 5\) cm.
- Using the formula \( P = 3a \):
- \( P = 3 \times 5 \)
- \( P = 15 \) cm
Hence, the perimeter of the equilateral triangle is 15 cm.
Example 2
Find the perimeter of an equilateral triangle where each side is 12 inches.
Solution:
- Given side length, \(a = 12\) inches.
- Using the formula \( P = 3a \):
- \( P = 3 \times 12 \)
- \( P = 36 \) inches
Therefore, the perimeter of the equilateral triangle is 36 inches.
In summary, the perimeter of an equilateral triangle is three times the length of one of its sides. This simple formula makes it easy to calculate the perimeter as long as the side length is known.
Perimeter of Isosceles Triangle
The perimeter of an isosceles triangle is calculated by summing the lengths of its three sides. An isosceles triangle has two sides of equal length, known as the legs, and a third side, known as the base.
The formula to calculate the perimeter \( P \) of an isosceles triangle is:
\( P = 2a + b \)
Where:
- \( a \) is the length of each of the two equal sides.
- \( b \) is the length of the base.
Example Calculation
Let's consider an example where the lengths of the equal sides \( a \) are 5 cm each, and the base \( b \) is 6 cm. To find the perimeter of this isosceles triangle:
\( P = 2a + b = 2(5 \, \text{cm}) + 6 \, \text{cm} = 10 \, \text{cm} + 6 \, \text{cm} = 16 \, \text{cm} \)
Thus, the perimeter of the isosceles triangle is 16 cm.
Units of Measurement for Area and Perimeter
Understanding the units of measurement for area and perimeter is essential in geometry, particularly when dealing with triangles. Here we outline the commonly used units and their applications.
Units of Measurement for Area
The area of a triangle is the amount of space enclosed within its boundaries. The units for measuring area are always in square units, as they represent the two-dimensional space covered by the shape. Common units include:
- Square meters (m2) - Used for larger surfaces like fields or rooms.
- Square centimeters (cm2) - Used for smaller surfaces like paper or small objects.
- Square millimeters (mm2) - Used for very small surfaces, such as the area of a microchip.
- Square inches (in2) - Common in countries using the imperial system, often for objects like screens or tiles.
- Square feet (ft2) - Also used in the imperial system, typically for larger surfaces like rooms or gardens.
Units of Measurement for Perimeter
The perimeter of a triangle is the total length around its three sides. The units for measuring perimeter are always linear units, as they represent one-dimensional lengths. Common units include:
- Meters (m) - Used for measuring the length of larger objects or distances.
- Centimeters (cm) - Used for measuring smaller objects or shorter lengths.
- Millimeters (mm) - Used for very small lengths or precision measurements.
- Inches (in) - Common in the imperial system for various lengths, such as the dimensions of small objects.
- Feet (ft) - Also used in the imperial system, typically for measuring larger lengths like the dimensions of a room.
Conversion Between Units
Sometimes, it is necessary to convert between different units of measurement. Here are some basic conversions:
| From | To | Conversion Factor |
|---|---|---|
| 1 meter (m) | 100 centimeters (cm) | 1 m = 100 cm |
| 1 centimeter (cm) | 10 millimeters (mm) | 1 cm = 10 mm |
| 1 meter (m) | 1000 millimeters (mm) | 1 m = 1000 mm |
| 1 foot (ft) | 12 inches (in) | 1 ft = 12 in |
| 1 inch (in) | 2.54 centimeters (cm) | 1 in = 2.54 cm |
By understanding these units and their conversions, you can accurately measure and calculate the area and perimeter of triangles in various contexts.
Frequently Asked Questions
-
Can the area of a triangle be negative?
No, the area of a triangle cannot be negative. Area represents a physical space, which cannot have a negative value.
-
Can a triangle have a perimeter of zero?
A triangle cannot have a zero perimeter. A triangle with zero perimeter does not exist because it means all its sides have zero lengths, which contradicts the definition of a triangle.
-
What if I know the lengths of the sides of the triangle, but not the height?
You can use Heron’s formula to calculate the area of a triangle when the lengths of all three sides are known. This formula doesn’t require the height.
-
Is the perimeter of a triangle always greater than its area?
Not necessarily. The relationship between a triangle’s area and its perimeter depends on the unit of measurement and the size of the triangle.
-
What is the formula for the perimeter of a triangle?
The perimeter of a triangle is calculated by simply adding the lengths of all three sides. The formula is:
\[ \text{Perimeter} = a + b + c \]
-
What is the area and perimeter of an equilateral triangle?
The area of an equilateral triangle is given by:
\[ A = \frac{\sqrt{3}}{4} \times (\text{side})^2 \]
The perimeter of an equilateral triangle is given by:
\[ P = 3 \times \text{side} \]
-
What is the general formula to find the area of a triangle?
The general formula to find the area of a triangle is:
\[ A = \frac{1}{2} \times \text{base} \times \text{height} \]
-
How do you calculate the perimeter of a triangle?
To calculate the perimeter of a triangle, add the lengths of all three sides. Ensure that the lengths are in the same unit.
Conclusion
In this guide, we have explored the various methods for calculating the area and perimeter of triangles, covering a range of formulas from basic to advanced. Understanding these concepts is crucial for anyone studying geometry, as triangles form the basis of many complex structures and designs.
The area of a triangle can be determined through different approaches depending on the available information. Whether using the base and height, Heron's formula, or the trigonometric method involving two sides and an included angle, each method offers a unique way to solve for the area. Similarly, calculating the perimeter involves summing the lengths of the triangle's sides, which is straightforward for equilateral and isosceles triangles, but can vary slightly for scalene triangles.
Mastering the area and perimeter of triangles not only enhances your mathematical skills but also allows you to appreciate the practical applications of these geometric principles. From architecture to engineering, triangles play a pivotal role in creating stable and efficient structures.
As you continue to delve into the world of geometry, remember that the journey of learning is continuous and ever-evolving. The concepts of area and perimeter are just the beginning, opening the door to a deeper understanding of mathematics and its real-world applications. Keep practicing, stay curious, and enjoy the process of discovery in the fascinating realm of geometry.
We hope this guide has provided you with a comprehensive understanding of the area and perimeter of triangles. Keep exploring, solving problems, and applying these principles to see the beauty and utility of mathematics in everyday life.
Hướng dẫn chi tiết cách tìm diện tích và chu vi của tam giác với Thầy J. Video này sẽ giúp bạn hiểu rõ hơn về các công thức và phương pháp tính toán trong hình học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác | Toán học với Thầy J
READ MORE:
Hướng dẫn chi tiết cách tìm diện tích và chu vi của tam giác. Video này sẽ giúp bạn hiểu rõ hơn về các công thức và phương pháp tính toán trong hình học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác