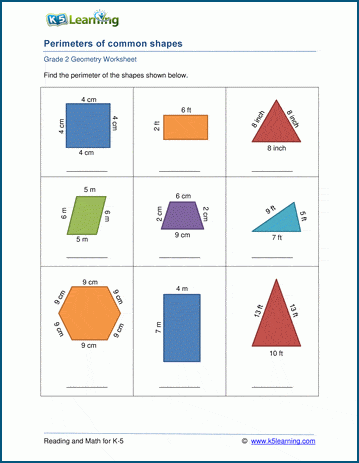
The Perimeter of the Scalene Triangle is 54.6 cm: How to Calculate and Understand It

The perimeter of a scalene triangle is the sum of the lengths of all its sides. For a scalene triangle, all three sides have different lengths. Given that the perimeter of the scalene triangle is 54.6 cm, we can represent the lengths of the sides as \( a \), \( b \), and \( c \).

Formula for Perimeter

The formula to calculate the perimeter (\( P \)) of a scalene triangle is:

\[ P = a + b + c \]

Given Information

In this problem, we are given that the perimeter is 54.6 cm. Thus, we have:

\[ a + b + c = 54.6 \, \text{cm} \]

Example Calculation

Suppose we have the following side lengths for the scalene triangle:

• Side \( a = 15.2 \, \text{cm} \)
• Side \( b = 20.4 \, \text{cm} \)
• Side \( c = 19.0 \, \text{cm} \)

We can check if these sides satisfy the given perimeter:

\[ a + b + c = 15.2 \, \text{cm} + 20.4 \, \text{cm} + 19.0 \, \text{cm} = 54.6 \, \text{cm} \]

Since the sum is 54.6 cm, these side lengths are a valid example for this scalene triangle.

Properties of a Scalene Triangle

• All sides have different lengths.
• All angles have different measures.
• It has no lines of symmetry.

Conclusion

Understanding the properties and the formula for the perimeter of a scalene triangle helps in solving problems related to the dimensions of the triangle. Given the perimeter, one can find various sets of side lengths that add up to the given perimeter.

A scalene triangle is a type of triangle where all three sides have different lengths, and all three angles have different measures. This lack of symmetry differentiates scalene triangles from other types, such as isosceles and equilateral triangles.

Key characteristics of scalene triangles include:

• Unequal Sides: Each side of a scalene triangle is a different length.
• Unequal Angles: The angles in a scalene triangle are all different, summing to 180 degrees.
• No Symmetry: Scalene triangles do not have lines of symmetry.

To understand scalene triangles better, it's crucial to know how to calculate their perimeter, which is the sum of the lengths of all three sides.

Given the perimeter of a scalene triangle is 54.6 cm, we use the formula:

\[ P = a + b + c \]

where \( P \) is the perimeter, and \( a \), \( b \), and \( c \) are the lengths of the sides. For instance, if the sides are \( a = 15.2 \, \text{cm} \), \( b = 20.4 \, \text{cm} \), and \( c = 19.0 \, \text{cm} \), we calculate:

\[ 15.2 \, \text{cm} + 20.4 \, \text{cm} + 19.0 \, \text{cm} = 54.6 \, \text{cm} \]

Understanding these basic properties and calculations lays the foundation for more advanced topics in geometry involving scalene triangles.

A scalene triangle is a type of triangle characterized by having all three sides of different lengths. This uniqueness extends to the angles, where each angle is also different, adding up to 180 degrees. Unlike isosceles and equilateral triangles, scalene triangles have no lines of symmetry.

The main properties of a scalene triangle include:

• Unequal Sides: Each side of a scalene triangle is a different length, making it distinct from other types of triangles.
• Unequal Angles: The internal angles are all different, ensuring no two angles are the same. The sum of these angles is always 180 degrees.
• No Symmetry: Scalene triangles do not have any lines of symmetry, which means there is no way to fold the triangle into equal halves.
• Perimeter: The perimeter of a scalene triangle is the sum of the lengths of its sides. For example, if the perimeter is 54.6 cm and the sides are \( a \), \( b \), and \( c \), then: \[ a + b + c = 54.6 \, \text{cm} \]
• Area Calculation: The area of a scalene triangle can be calculated using Heron's formula, which is: \[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \] where \( s \) is the semi-perimeter: \[ s = \frac{a + b + c}{2} \]

These properties make scalene triangles an interesting subject of study in geometry, offering various applications in real-world scenarios and mathematical problems.

The perimeter of a triangle is the total length around the triangle, calculated by adding the lengths of its three sides. For a scalene triangle, where all sides have different lengths, the formula to find the perimeter (\( P \)) is straightforward:

\[ P = a + b + c \]

Given the problem where the perimeter of the scalene triangle is 54.6 cm, let's break down the process step by step.

Step-by-Step Calculation

To understand the perimeter calculation, consider the following steps:

1. Identify the Side Lengths: Let's denote the sides of the triangle as \( a \), \( b \), and \( c \). These are all different in a scalene triangle.
2. Sum the Side Lengths: Using the formula for the perimeter, add the lengths of the three sides:

   
   \[ P = a + b + c \]

3. Example Calculation: Suppose the side lengths are \( a = 15.2 \, \text{cm} \), \( b = 20.4 \, \text{cm} \), and \( c = 19.0 \, \text{cm} \). To find the perimeter:

   
   \[ P = 15.2 \, \text{cm} + 20.4 \, \text{cm} + 19.0 \, \text{cm} \]
   \[ P = 54.6 \, \text{cm} \]

Properties of the Perimeter

• Linear Measure: The perimeter is a linear measurement, representing the total distance around the triangle.
• Dependence on Side Lengths: The value of the perimeter directly depends on the individual lengths of the sides.
• Units: The units of the perimeter are the same as the units of the side lengths (e.g., centimeters, meters).

Understanding the perimeter of a scalene triangle is crucial for solving various geometric problems and for practical applications in fields such as engineering and architecture. By mastering this concept, you can easily tackle related challenges with confidence.

To calculate the perimeter of a scalene triangle, you need to know the lengths of all three sides. The formula for the perimeter \( P \) of a scalene triangle is:

\[ P = a + b + c \]

Here, \( a \), \( b \), and \( c \) represent the lengths of the sides of the triangle. Let's go through the steps with a specific example:

Example Problem

Suppose we have a scalene triangle where:

• Side \( a = 8.7 \, \text{cm} \)
• Side \( c = 26.1 \, \text{cm} \)
• The perimeter \( P = 54.6 \, \text{cm} \)

We need to find the length of side \( b \). Using the perimeter formula:

\[ P = a + b + c \]

Substitute the known values into the formula:

\[ 54.6 = 8.7 + b + 26.1 \]

Combine the known side lengths:

\[ 54.6 = 34.8 + b \]

Solve for \( b \) by isolating it on one side of the equation:

\[ b = 54.6 - 34.8 \]

Perform the subtraction:

\[ b = 19.8 \, \text{cm} \]

Thus, the length of side \( b \) is \( 19.8 \, \text{cm} \).

General Steps

1. Write down the perimeter formula: \( P = a + b + c \).
2. Substitute the known values into the formula.
3. Combine like terms to simplify the equation.
4. Isolate the unknown side length and solve for it.

By following these steps, you can calculate the perimeter of any scalene triangle as long as you have the lengths of its sides.

Here are some example problems to help you understand how to calculate the perimeter of a scalene triangle.

Example 1

Given a scalene triangle with sides \(a = 8.7 \, \text{cm}\), \(b\), and \(c = 26.1 \, \text{cm}\), and the perimeter is \(54.6 \, \text{cm}\). Find the length of side \(b\).

To find the value of \(b\), we use the formula for the perimeter of a triangle:

\[ P = a + b + c \]

Substituting the known values:

\[ 54.6 = 8.7 + b + 26.1 \]

Simplifying the equation:

\[ 54.6 = 34.8 + b \]

Solving for \(b\):

\[ b = 54.6 - 34.8 \]

Therefore,

\[ b = 19.8 \, \text{cm} \]

Example 2

Consider a scalene triangle where the sides are \(a = 10 \, \text{cm}\), \(b = 15 \, \text{cm}\), and \(c = 20 \, \text{cm}\). Calculate the perimeter of the triangle.

Using the perimeter formula:

\[ P = a + b + c \]

Substituting the given values:

\[ P = 10 + 15 + 20 \]

Therefore, the perimeter is:

\[ P = 45 \, \text{cm} \]

Example 3

A scalene triangle has a perimeter of \(60 \, \text{cm}\). If two sides are \(a = 18 \, \text{cm}\) and \(b = 22 \, \text{cm}\), find the length of the third side \(c\).

We know:

\[ P = a + b + c \]

Given:

\[ 60 = 18 + 22 + c \]

Simplifying the equation:

\[ 60 = 40 + c \]

Solving for \(c\):

\[ c = 60 - 40 \]

Therefore,

\[ c = 20 \, \text{cm} \]

Practice Problem

Try solving this problem on your own:

Given a scalene triangle with sides \(a = 12 \, \text{cm}\), \(b = 17 \, \text{cm}\), and the perimeter is \(50 \, \text{cm}\). Find the length of the third side \(c\).

Hint: Use the formula for the perimeter and solve for \(c\).

Scalene triangles, characterized by their three unequal sides and different angle measures, have a variety of practical applications in geometry and beyond. Understanding these applications provides insight into how geometric principles are utilized in real-world scenarios.

1. Architecture and Construction

In architecture and construction, the properties of scalene triangles are crucial for designing and creating unique structures. Scalene triangles are often used in roof trusses and bridges to provide strength and stability. Their unequal sides allow for the distribution of weight and force in a way that can accommodate complex architectural designs.

2. Land Surveying

Surveyors frequently encounter irregularly shaped plots of land, which can be approximated using scalene triangles. Calculating the perimeter and area of these triangles helps in determining the exact size and boundaries of the land. This application is essential for creating accurate maps and legal documents.

3. Fashion and Design

In fashion design, scalene triangles are used to create patterns and garment pieces that require precise measurements. Designers use these triangles to cut fabrics in shapes that fit together perfectly, ensuring the final product is both functional and aesthetically pleasing.

4. Navigation and Mapping

Scalene triangles play a significant role in navigation and mapping, particularly in calculating distances between points on uneven terrains. Navigators use the properties of these triangles to chart courses and measure distances accurately, especially in maritime and aviation contexts.

5. Engineering and Mechanics

Engineers use scalene triangles in various mechanical designs where unequal forces need to be balanced. For example, in the design of trusses and mechanical linkages, the unequal sides of scalene triangles help distribute forces efficiently, ensuring the stability and functionality of the structure or mechanism.

Examples in Real Life

• Roof Trusses: The triangular shapes in roof trusses often use scalene triangles to provide stability and support to the roof structure.
• Bridges: Scalene triangles are used in the construction of bridges to evenly distribute loads and enhance structural integrity.
• Land Plots: Surveyors use scalene triangles to measure irregular land plots, aiding in accurate land division and mapping.
• Garment Patterns: Fashion designers use scalene triangles to create precise fabric cuts for better fitting garments.

These applications highlight the versatility and importance of scalene triangles in various fields, demonstrating how a fundamental geometric concept can have widespread practical uses.

When calculating the perimeter of a scalene triangle, several common mistakes can occur. Here are some key points to keep in mind to avoid these errors:

• Incorrect Side Lengths:

  Ensure that you accurately measure all three sides of the triangle. A common mistake is assuming one side length based on incorrect measurements or estimations.

• Sum of the Sides:

  Remember that the perimeter of a scalene triangle is the sum of all three sides. The formula is:

  \[ P = a + b + c \]

  Where \( a \), \( b \), and \( c \) are the lengths of the sides.

• Unit Consistency:

  All side lengths must be in the same unit when calculating the perimeter. Converting units improperly can lead to incorrect results.

• Using the Correct Formula:

  Ensure you use the correct formula for the type of triangle you are dealing with. For a scalene triangle, no sides or angles are equal, so the simple sum formula applies.

Tips for Accurate Calculation:

1. Double-Check Measurements: Always remeasure the sides to ensure accuracy before performing calculations.

2. Use Appropriate Tools: Use precise measuring tools such as a ruler or a measuring tape for physical triangles, or reliable software for virtual triangles.

3. Verify Units: Ensure all measurements are in the same unit. Convert if necessary before adding the side lengths.

4. Cross-Verify Results: After calculating the perimeter, cross-verify by adding the sides again to confirm the result.

By following these tips and being aware of common mistakes, you can accurately calculate the perimeter of a scalene triangle every time.

In this section, we will explore more advanced concepts related to scalene triangles, focusing on perimeter calculations, properties, and applications.

Perimeter of a Scalene Triangle with Given Sides

The perimeter of a scalene triangle is simply the sum of the lengths of its three sides. Given a scalene triangle with side lengths \( a \), \( b \), and \( c \), the perimeter \( P \) is calculated as:

\[ P = a + b + c \]

For example, if a scalene triangle has side lengths of 15.2 cm, 20.4 cm, and 19 cm, its perimeter would be:

\[ P = 15.2 \, \text{cm} + 20.4 \, \text{cm} + 19 \, \text{cm} = 54.6 \, \text{cm} \]

Heron's Formula for Area

Heron's formula provides a method to calculate the area of a triangle when the lengths of all three sides are known. Given a scalene triangle with side lengths \( a \), \( b \), and \( c \), the area \( A \) can be found as follows:

1. Calculate the semi-perimeter \( s \):

   
   \[ s = \frac{a + b + c}{2} \]

2. Use the semi-perimeter to find the area:

   
   \[ A = \sqrt{s(s-a)(s-b)(s-c)} \]

Internal and External Angle Bisectors

In a scalene triangle, the internal angle bisectors are the lines that divide each internal angle into two equal parts, while the external angle bisectors extend the sides of the triangle to form external angles. Understanding these bisectors is crucial for advanced geometric constructions and proofs.

Medians and Centroid

A median of a scalene triangle is a line segment joining a vertex to the midpoint of the opposite side. The three medians intersect at a point known as the centroid, which has several important properties:

• The centroid divides each median into two segments, with the segment connecting the vertex to the centroid being twice as long as the segment connecting the centroid to the midpoint of the opposite side.
• The centroid is the center of mass or balance point of the triangle.

Orthocenter, Circumcenter, and Incenter

• Orthocenter: The point where the three altitudes of a triangle intersect. In a scalene triangle, this point can lie inside or outside the triangle.
• Circumcenter: The point where the perpendicular bisectors of the sides of the triangle intersect. This point is the center of the circumcircle, which passes through all three vertices of the triangle.
• Incenter: The point where the internal angle bisectors intersect. This point is the center of the incircle, which is tangent to all three sides of the triangle.

Advanced Applications

Scalene triangles are used in various advanced applications such as:

• Trigonometry: In solving problems involving the Law of Sines and the Law of Cosines.
• Engineering: In the design of structures where non-equilateral triangles provide necessary stability.
• Computer Graphics: For mesh generation and surface modeling where non-uniform shapes are required.

Below are some practice problems and detailed solutions to help reinforce your understanding of the perimeter of scalene triangles.

Problem 1

The perimeter of a scalene triangle is 54.6 cm. If one side measures 8.7 cm and another side measures 26.1 cm, find the length of the third side.

1. First, use the perimeter formula:

   
   \[ P = a + b + c \]

2. Substitute the known values into the formula:

   
   \[ 54.6 = 8.7 + 26.1 + b \]

3. Simplify the equation to solve for \( b \):

   
   \[ 54.6 = 34.8 + b \]
   \[ b = 54.6 - 34.8 \]
   \[ b = 19.8 \, \text{cm} \]

Solution: The length of the third side is 19.8 cm.

Problem 2

A scalene triangle has sides of length 12.3 cm, 15.4 cm, and 18.9 cm. Calculate its perimeter.

1. Add the lengths of all three sides:

   
   \[ P = 12.3 + 15.4 + 18.9 \]

2. Perform the addition:

   
   \[ P = 46.6 \, \text{cm} \]

Solution: The perimeter of the triangle is 46.6 cm.

Problem 3

Given a scalene triangle with sides \( a = 10 \, \text{cm} \), \( b = 12 \, \text{cm} \), and \( c = 14 \, \text{cm} \), verify the perimeter calculation.

1. Use the perimeter formula:

   
   \[ P = a + b + c \]

2. Substitute the given values:

   
   \[ P = 10 + 12 + 14 \]

3. Add the side lengths:

   
   \[ P = 36 \, \text{cm} \]

Solution: The calculated perimeter is correct at 36 cm.

Problem 4

Find the perimeter of a scalene triangle with sides measuring \( 9.5 \, \text{cm} \), \( 13.2 \, \text{cm} \), and \( 17.9 \, \text{cm} \).

1. Sum the side lengths:

   
   \[ P = 9.5 + 13.2 + 17.9 \]

2. Calculate the total:

   
   \[ P = 40.6 \, \text{cm} \]

Solution: The perimeter of the triangle is 40.6 cm.

Problem 5

The perimeter of a scalene triangle is 54.6 cm. If one side is three times the shortest side which measures 8.7 cm, find the length of the third side.

1. Let the sides be \( a = 8.7 \, \text{cm} \), \( b = 3a = 3 \times 8.7 \, \text{cm} = 26.1 \, \text{cm} \), and \( c \).
2. Use the perimeter formula:

   
   \[ 54.6 = 8.7 + 26.1 + c \]

3. Solve for \( c \):

   
   \[ 54.6 = 34.8 + c \]
   \[ c = 54.6 - 34.8 \]
   \[ c = 19.8 \, \text{cm} \]

Solution: The third side measures 19.8 cm.