Topic what is the perimeter of this triangle: Understanding the perimeter of a triangle is crucial for solving many geometric problems and real-world applications. This guide will teach you how to calculate the perimeter of any triangle effortlessly. Whether dealing with equilateral, isosceles, or scalene triangles, we’ll break down the steps to find the perimeter with ease. Dive in to master these essential skills!
Table of Content
- Calculating the Perimeter of a Triangle
- Introduction to Triangle Perimeter
- Basic Definition and Formula
- Different Types of Triangles
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
- Example Calculations
- Applications of Triangle Perimeter
- Special Considerations in Perimeter Calculations
- Perimeter in Different Units
- Perimeter of Right-Angled Triangle
- Using Perimeter in Real-World Problems
- Common Mistakes and How to Avoid Them
- FAQs on Triangle Perimeter
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách tìm chu vi tam giác. Thích hợp cho những ai đang tìm hiểu về chu vi của tam giác.
Calculating the Perimeter of a Triangle
The perimeter of a triangle is the total length around the triangle, which is calculated by adding the lengths of all its sides.
Formula for the Perimeter
Given a triangle with side lengths \( a \), \( b \), and \( c \), the perimeter \( P \) can be calculated using the formula:
\( P = a + b + c \)
Example Calculation
Consider a triangle with side lengths \( a = 3 \, \text{units} \), \( b = 4 \, \text{units} \), and \( c = 5 \, \text{units} \). Using the formula, the perimeter can be calculated as:
\( P = 3 + 4 + 5 = 12 \, \text{units} \)
Special Cases
- Equilateral Triangle: All sides are equal, so the perimeter is \( 3 \times \text{side length} \).
- Isosceles Triangle: Two sides are equal. If the equal sides are \( a \), the formula is \( P = 2a + b \).
- Scalene Triangle: All sides are different, so the perimeter is simply \( a + b + c \).
Applications
Knowing the perimeter is useful in various real-life applications, such as:
- Determining the amount of material needed to build a triangular frame.
- Calculating the boundary length for a triangular plot of land.
- Solving problems in fields like engineering, architecture, and art.
Additional Considerations
When calculating the perimeter, ensure that all side lengths are in the same unit. If the triangle's side lengths are given in different units, convert them to a common unit before summing them up.
| Type of Triangle | Formula |
|---|---|
| Equilateral Triangle | \( P = 3a \) |
| Isosceles Triangle | \( P = 2a + b \) |
| Scalene Triangle | \( P = a + b + c \) |

READ MORE:
Introduction to Triangle Perimeter
The perimeter of a triangle is the total distance around the triangle. It is a fundamental concept in geometry that applies to all types of triangles, whether equilateral, isosceles, or scalene. Understanding how to calculate the perimeter is essential for solving geometric problems and practical applications.
A triangle is defined by three sides. The perimeter is simply the sum of the lengths of these sides. For a triangle with sides \( a \), \( b \), and \( c \), the formula to find the perimeter \( P \) is:
\( P = a + b + c \)
Here’s how to calculate the perimeter of different types of triangles:
- Equilateral Triangle: All three sides are equal. If each side length is \( a \), the perimeter is \( P = 3a \).
- Isosceles Triangle: Two sides are equal. If the equal sides are \( a \) and the base is \( b \), the perimeter is \( P = 2a + b \).
- Scalene Triangle: All sides are different. The perimeter is simply \( P = a + b + c \).
Let’s break down the steps to calculate the perimeter:
- Identify the lengths of all three sides of the triangle.
- Add these lengths together to get the total distance around the triangle.
For example, consider a triangle with sides \( a = 5 \, \text{units} \), \( b = 7 \, \text{units} \), and \( c = 10 \, \text{units} \). The perimeter is:
\( P = 5 + 7 + 10 = 22 \, \text{units} \)
Understanding the perimeter is not only useful for academic purposes but also has practical applications in fields like construction, art, and design. It helps in determining the amount of material needed for boundaries and frames.
Basic Definition and Formula
The perimeter of a triangle is the total length of its three sides. This concept is fundamental in geometry, where understanding how to calculate the perimeter is crucial for various applications and problem-solving scenarios.
For any triangle with side lengths \( a \), \( b \), and \( c \), the perimeter \( P \) is given by the simple formula:
\( P = a + b + c \)
Here's how to apply the formula step-by-step:
- Identify the lengths of each side of the triangle. These sides are usually denoted as \( a \), \( b \), and \( c \).
- Add the lengths of the three sides together.
This formula is universal and applies to all types of triangles. Let’s consider each type:
- Equilateral Triangle: All three sides are equal in length. If each side is \( a \), then the perimeter is \( P = 3a \). For example, if each side is 5 units, the perimeter is:
- Isosceles Triangle: Two sides are equal in length, say \( a \). The third side, \( b \), is different. The perimeter is \( P = 2a + b \). For instance, if the equal sides are 4 units each and the base is 6 units, the perimeter is:
- Scalene Triangle: All three sides are of different lengths. The perimeter is the sum of all three sides, \( P = a + b + c \). For example, with side lengths of 3 units, 4 units, and 5 units, the perimeter is:
\( P = 3 \times 5 = 15 \, \text{units} \)
\( P = 2 \times 4 + 6 = 14 \, \text{units} \)
\( P = 3 + 4 + 5 = 12 \, \text{units} \)
Calculating the perimeter is straightforward and involves just adding the side lengths. This simplicity makes it an essential tool in various practical applications, from determining the amount of fencing needed around a triangular plot to creating designs in art and architecture.
Different Types of Triangles
Triangles are classified based on the lengths of their sides and the measures of their angles. Understanding these types helps in calculating the perimeter and solving various geometric problems. Below, we explore the three main types of triangles based on side lengths and how their perimeters are calculated.
- Equilateral Triangle:
An equilateral triangle has all three sides of equal length. Consequently, each of its three angles is also equal, measuring 60 degrees. The formula for the perimeter of an equilateral triangle, where each side is \( a \), is:
\( P = 3a \)
For example, if each side is 6 units, the perimeter is:
\( P = 3 \times 6 = 18 \, \text{units} \)
- Isosceles Triangle:
An isosceles triangle has two sides of equal length, and these sides are called the legs. The third side, known as the base, is of a different length. The two equal angles opposite the legs are also equal. The formula for the perimeter of an isosceles triangle, where the equal sides are \( a \) and the base is \( b \), is:
\( P = 2a + b \)
For instance, if the legs are 5 units each and the base is 8 units, the perimeter is:
\( P = 2 \times 5 + 8 = 18 \, \text{units} \)
- Scalene Triangle:
A scalene triangle has all three sides of different lengths. This means that all three angles are also different. The formula for the perimeter of a scalene triangle, where the sides are \( a \), \( b \), and \( c \), is simply:
\( P = a + b + c \)
As an example, for a triangle with side lengths 7 units, 10 units, and 12 units, the perimeter is:
\( P = 7 + 10 + 12 = 29 \, \text{units} \)
Each type of triangle has unique properties that determine how the perimeter is calculated. Knowing these distinctions is essential for applying the correct formula and understanding the triangle's geometry.
Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are equal in length, and all three interior angles are equal, each measuring \(60^\circ\). This uniformity makes it one of the simplest triangles to work with in geometry.
The defining properties of an equilateral triangle include:
- Equal Sides: All three sides have the same length, denoted as \( a \).
- Equal Angles: Each of the three angles is \(60^\circ\).
- Symmetry: It has three lines of symmetry and rotational symmetry of order 3.
The formula to calculate the perimeter \( P \) of an equilateral triangle is straightforward since all sides are equal:
\( P = 3a \)
Here's how to calculate the perimeter step-by-step:
- Determine the length of one side of the triangle, \( a \).
- Multiply this length by 3 to account for all three sides being equal.
For example, if each side of an equilateral triangle is 8 units, the perimeter is calculated as:
\( P = 3 \times 8 = 24 \, \text{units} \)
This simple formula and calculation make equilateral triangles particularly useful in various applications, from architectural designs to tessellations in art. The equal side lengths also simplify many geometric problems and proofs.
| Property | Description |
|---|---|
| Sides | All sides are equal, denoted as \( a \). |
| Angles | All interior angles are equal, each measuring \(60^\circ\). |
| Perimeter | Calculated as \( 3a \). |
| Symmetry | Three lines of symmetry and rotational symmetry of order 3. |
In summary, the equilateral triangle's simplicity and symmetry make it a foundational shape in geometry. Knowing how to calculate its perimeter is a basic yet essential skill.
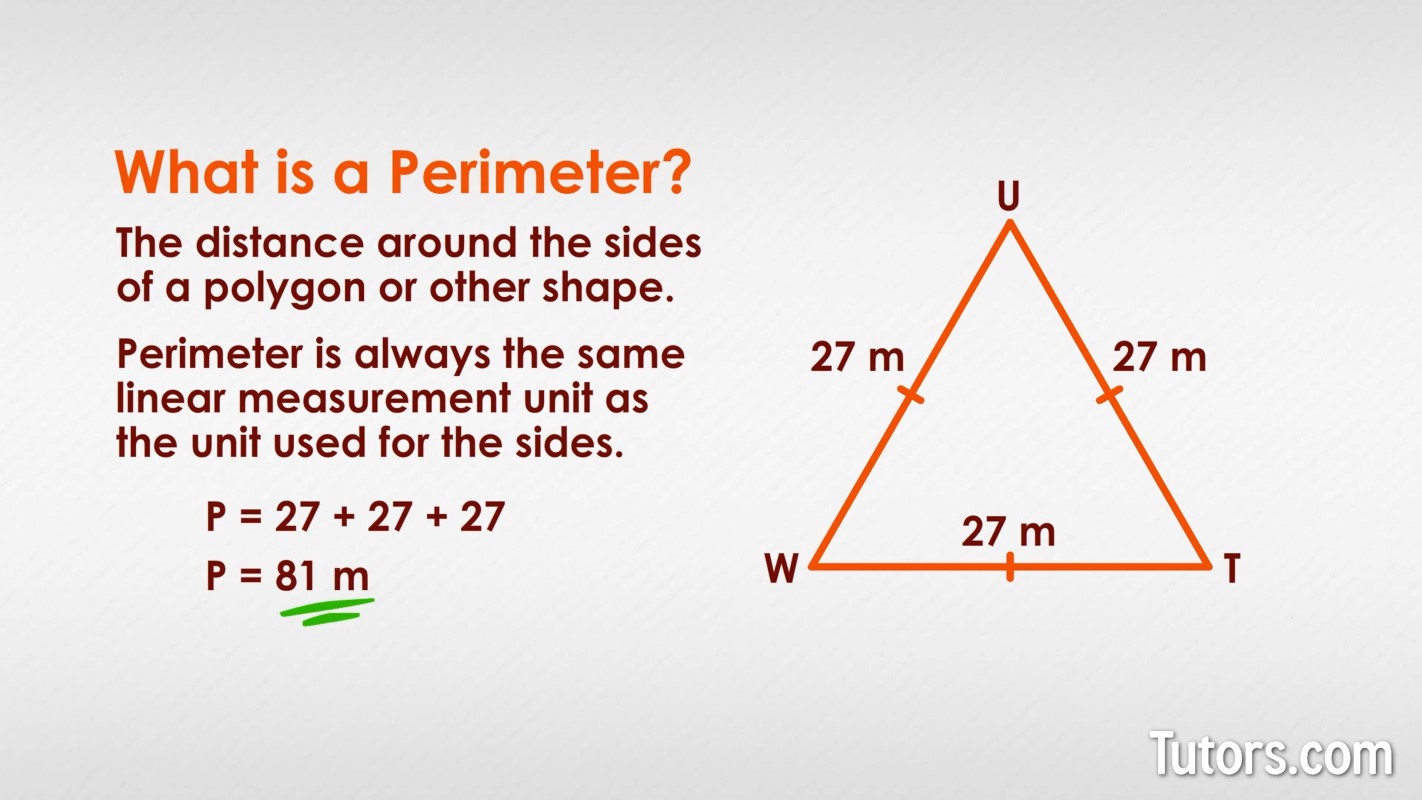
Isosceles Triangle
An isosceles triangle is characterized by having at least two sides of equal length. The angles opposite these equal sides are also equal, giving the triangle a unique balance. This geometric property makes the isosceles triangle a common and important shape in various mathematical contexts.
Key properties of an isosceles triangle include:
- Two Equal Sides: These sides, known as the legs, are denoted as \( a \).
- Base: The third side, different in length, is called the base, denoted as \( b \).
- Equal Angles: The angles opposite the equal sides are congruent.
- Axis of Symmetry: The triangle has one line of symmetry that bisects the base and the opposite angle.
The formula to calculate the perimeter \( P \) of an isosceles triangle is:
\( P = 2a + b \)
Here’s how to calculate the perimeter step-by-step:
- Measure the lengths of the two equal sides, each denoted as \( a \).
- Measure the length of the base, denoted as \( b \).
- Add the lengths of the two equal sides and the base together using the formula \( P = 2a + b \).
For example, if the legs of an isosceles triangle are each 7 units and the base is 10 units, the perimeter is:
\( P = 2 \times 7 + 10 = 24 \, \text{units} \)
The simplicity of this formula makes it easy to calculate the perimeter for various applications, from solving problems in geometry to designing structures that incorporate isosceles triangles.
| Property | Description |
|---|---|
| Sides | Two sides are equal in length, denoted as \( a \). The base is a different length, denoted as \( b \). |
| Angles | The angles opposite the equal sides are equal. |
| Perimeter | Calculated as \( 2a + b \). |
| Symmetry | One line of symmetry that divides the triangle into two mirror-image halves. |
Understanding the properties and perimeter calculation of an isosceles triangle is fundamental in geometry and various practical applications, from construction to art.
Scalene Triangle
A scalene triangle is a type of triangle where all three sides are of different lengths, and all three angles are different. This lack of symmetry gives the scalene triangle unique properties and makes it a versatile shape in geometry.
Key characteristics of a scalene triangle include:
- Unequal Sides: Each of the three sides has a different length, denoted as \( a \), \( b \), and \( c \).
- Unique Angles: Each of the three interior angles is different in measure.
- No Symmetry: A scalene triangle has no lines of symmetry.
The formula to calculate the perimeter \( P \) of a scalene triangle is simply the sum of its side lengths:
\( P = a + b + c \)
To calculate the perimeter of a scalene triangle, follow these steps:
- Measure the lengths of all three sides. These sides are usually denoted as \( a \), \( b \), and \( c \).
- Add the lengths of these sides together using the formula \( P = a + b + c \).
For instance, if a scalene triangle has sides of 5 units, 9 units, and 12 units, the perimeter is:
\( P = 5 + 9 + 12 = 26 \, \text{units} \)
The lack of equal sides and angles in a scalene triangle means that no simple shortcuts can be used to find the perimeter other than directly summing the side lengths. This straightforward approach is practical in various scenarios, such as determining the boundary length of a triangular plot of land with uneven sides.
| Property | Description |
|---|---|
| Sides | All sides are of different lengths, denoted as \( a \), \( b \), and \( c \). |
| Angles | All angles are of different measures. |
| Perimeter | Calculated as \( a + b + c \). |
| Symmetry | No lines of symmetry. |
In summary, the scalene triangle's distinct sides and angles make it a unique shape with no symmetry. Calculating its perimeter is straightforward, requiring only the addition of its side lengths, which is essential for solving various geometric and practical problems.
Example Calculations
Calculating the perimeter of a triangle involves adding the lengths of its sides. Below, we provide detailed step-by-step examples for different types of triangles to illustrate how to determine their perimeters.
1. Equilateral Triangle
In an equilateral triangle, all sides are equal. If each side of the triangle is \( a \) units, the perimeter \( P \) is calculated as:
\( P = 3a \)
Example: Calculate the perimeter of an equilateral triangle with each side measuring 6 units.
- Identify the length of one side: \( a = 6 \, \text{units} \).
- Apply the formula: \( P = 3 \times 6 \).
- Calculate the perimeter: \( P = 18 \, \text{units} \).
Thus, the perimeter of the equilateral triangle is 18 units.
2. Isosceles Triangle
In an isosceles triangle, two sides are equal in length. If the equal sides are each \( a \) units and the base is \( b \) units, the perimeter \( P \) is given by:
\( P = 2a + b \)
Example: Calculate the perimeter of an isosceles triangle with equal sides of 7 units each and a base of 10 units.
- Identify the lengths of the equal sides: \( a = 7 \, \text{units} \).
- Identify the length of the base: \( b = 10 \, \text{units} \).
- Apply the formula: \( P = 2 \times 7 + 10 \).
- Calculate the perimeter: \( P = 14 + 10 = 24 \, \text{units} \).
Therefore, the perimeter of the isosceles triangle is 24 units.
3. Scalene Triangle
In a scalene triangle, all sides have different lengths. If the sides are \( a \), \( b \), and \( c \), the perimeter \( P \) is calculated as:
\( P = a + b + c \)
Example: Calculate the perimeter of a scalene triangle with sides measuring 5 units, 9 units, and 12 units.
- Identify the lengths of all three sides: \( a = 5 \, \text{units} \), \( b = 9 \, \text{units} \), \( c = 12 \, \text{units} \).
- Apply the formula: \( P = 5 + 9 + 12 \).
- Calculate the perimeter: \( P = 26 \, \text{units} \).
Thus, the perimeter of the scalene triangle is 26 units.
Summary Table
The table below summarizes the perimeter calculations for each type of triangle:
| Triangle Type | Formula | Example | Perimeter |
|---|---|---|---|
| Equilateral Triangle | \( P = 3a \) | Side length \( a = 6 \, \text{units} \) | \( P = 18 \, \text{units} \) |
| Isosceles Triangle | \( P = 2a + b \) | Equal sides \( a = 7 \, \text{units} \), base \( b = 10 \, \text{units} \) | \( P = 24 \, \text{units} \) |
| Scalene Triangle | \( P = a + b + c \) | Sides \( a = 5 \, \text{units} \), \( b = 9 \, \text{units} \), \( c = 12 \, \text{units} \) | \( P = 26 \, \text{units} \) |
By following these step-by-step examples and using the appropriate formulas, you can easily calculate the perimeter of any triangle, whether it is equilateral, isosceles, or scalene.
Applications of Triangle Perimeter
The perimeter of a triangle is a fundamental concept in geometry with numerous practical applications in various fields. Below are some detailed examples of how the perimeter of a triangle is used in real-world scenarios:
-
Construction and Architecture:
When designing and constructing buildings, the perimeter of triangular elements is essential for determining the amount of materials required. For example, in constructing a triangular garden, the perimeter helps in calculating the total length of fencing needed to enclose the area.
-
Landscaping:
In landscaping, knowing the perimeter of triangular plots helps in estimating the quantity of materials such as turf, soil, and decorative stones needed. For instance, to create a triangular flower bed, you need to know the perimeter to determine the border length for planting or adding edging materials.
-
Surveying and Land Measurement:
Surveyors use the perimeter of triangular plots to measure land accurately. This is crucial in determining property boundaries, dividing land into parcels, and calculating the area for agricultural or developmental purposes.
-
Manufacturing:
In manufacturing, particularly in fabricating components with triangular shapes, the perimeter helps in determining the amount of material required. For example, when cutting fabric for triangular banners or sails, knowing the perimeter ensures precise material usage and minimizes waste.
-
Art and Design:
Artists and designers often use triangular shapes in their works. Understanding the perimeter allows them to create balanced and proportionate designs. For example, in creating a piece of stained glass art with triangular sections, knowing the perimeter helps in accurately cutting and fitting the glass pieces.
-
Education:
In educational settings, problems involving the perimeter of triangles help students develop their mathematical skills. These exercises can range from simple calculations to complex real-life applications, enhancing their understanding of geometry and its practical uses.
Overall, the concept of the perimeter of a triangle is applied across various disciplines, showcasing its importance in both theoretical and practical contexts.
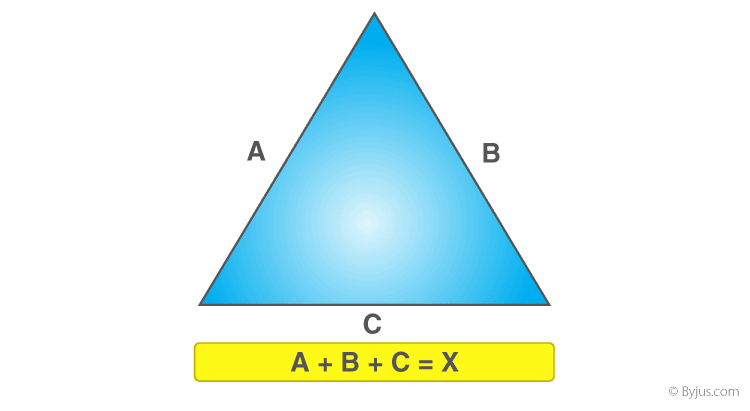
Special Considerations in Perimeter Calculations
When calculating the perimeter of a triangle, there are several special considerations to keep in mind to ensure accurate results. Below are key points to consider:
- Units Consistency: Ensure that all side lengths are in the same unit before performing any calculations. Convert units if necessary to maintain consistency.
- Triangle Inequality Theorem: Verify that the given side lengths satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides must be greater than the length of the remaining side.
- Types of Triangles:
- Equilateral Triangle: For an equilateral triangle, the perimeter is calculated as \( P = 3a \), where \( a \) is the length of each side.
- Isosceles Triangle: For an isosceles triangle with two equal sides \( a \) and base \( b \), the perimeter is \( P = 2a + b \).
- Scalene Triangle: For a scalene triangle, simply sum the lengths of all three sides, \( P = a + b + c \).
- Right-Angled Triangle: If the triangle is right-angled, use the Pythagorean theorem to find the hypotenuse if it's not provided. The perimeter is then the sum of the two legs and the hypotenuse, \( P = a + b + \sqrt{a^2 + b^2} \).
- Use of Trigonometric Functions: In cases where only two sides and an included angle (SAS) are known, use the Law of Cosines to find the third side. For two angles and a side (ASA), use the Law of Sines to find the remaining sides before summing them to find the perimeter.
- Precision and Rounding: Maintain consistent precision throughout the calculations, especially when dealing with irrational numbers or trigonometric calculations. Round the final result to the desired level of accuracy, typically to two decimal places.
By keeping these considerations in mind, you can accurately calculate the perimeter of various types of triangles in different scenarios.
Perimeter in Different Units
When calculating the perimeter of a triangle, it is essential to ensure that all measurements are in the same unit before performing the addition. Converting units correctly will ensure the accuracy of your calculation. Below, we will discuss how to handle different units and convert between them effectively.
Basic Formula
The basic formula for the perimeter of a triangle is:
\[
\text{Perimeter} = a + b + c
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Unit Conversion
Common units of length include millimeters (mm), centimeters (cm), meters (m), and kilometers (km). Here are some conversion factors to help you convert between these units:
- 1 cm = 10 mm
- 1 m = 100 cm
- 1 km = 1000 m
To convert from one unit to another, use multiplication or division based on these conversion factors. For example, to convert 150 cm to meters:
\[
150 \, \text{cm} \div 100 = 1.5 \, \text{m}
\]
Example Calculation
Consider a triangle with sides of 3 meters, 50 centimeters, and 1500 millimeters. First, convert all measurements to the same unit, meters:
- 3 meters (already in meters)
- 50 cm = 0.5 meters (since \(50 \div 100 = 0.5\))
- 1500 mm = 1.5 meters (since \(1500 \div 1000 = 1.5\))
Now, calculate the perimeter:
\[
\text{Perimeter} = 3 \, \text{m} + 0.5 \, \text{m} + 1.5 \, \text{m} = 5 \, \text{m}
\]
Perimeter in Various Units
Sometimes you may need the perimeter in a different unit after calculating it. For instance, if you need the perimeter in centimeters:
\[
5 \, \text{m} = 500 \, \text{cm} \quad (\text{since } 5 \times 100 = 500)
\]
Special Considerations
Here are some tips for working with units:
- Always double-check your conversions to avoid errors.
- Use consistent units throughout the calculation to simplify the process.
- Convert final results to the desired unit for your application.
Applications
Accurate perimeter calculations in the correct units are crucial in various real-world applications such as construction, tailoring, and any field requiring precise measurements.
Perimeter of Right-Angled Triangle
The perimeter of a right-angled triangle is the sum of the lengths of all its sides. In a right-angled triangle, one angle is exactly 90 degrees, and the side opposite this angle is called the hypotenuse, denoted as \( c \). The other two sides are referred to as the legs, denoted as \( a \) and \( b \).
The formula to calculate the perimeter \( P \) of a right-angled triangle is:
\[
P = a + b + c
\]
To find the hypotenuse when the lengths of the legs are known, we use the Pythagorean Theorem:
\[
c = \sqrt{a^2 + b^2}
\]
Therefore, the perimeter can be written as:
\[
P = a + b + \sqrt{a^2 + b^2}
\]
Example Calculation
Let's calculate the perimeter of a right-angled triangle where the lengths of the legs are \( a = 3 \) units and \( b = 4 \) units.
- First, calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Then, find the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Special Right Triangles
There are specific types of right-angled triangles with fixed angle ratios that simplify calculations:
- 30°-60°-90° Triangle: The side lengths are in the ratio 1 : \(\sqrt{3}\) : 2.
- 45°-45°-90° Triangle: The side lengths are in the ratio 1 : 1 : \(\sqrt{2}\).
Application Example
For a 30°-60°-90° triangle, if the shortest side \( a \) (opposite the 30° angle) is 5 units:
- Calculate the other sides using the ratio:
- \( b = a \cdot \sqrt{3} = 5 \cdot \sqrt{3} \approx 8.66 \)
- \( c = 2a = 2 \cdot 5 = 10 \)
- Find the perimeter:
\[
P = 5 + 8.66 + 10 \approx 23.66 \text{ units}
\]
Real-World Applications
Understanding the perimeter of right-angled triangles is useful in various real-world applications such as construction, navigation, and design, where accurate measurements and calculations are essential for creating structures, maps, and various projects.
Using Perimeter in Real-World Problems
The concept of the perimeter of a triangle has various practical applications in real-world scenarios. Understanding these applications helps to appreciate the significance of perimeter calculations in different contexts.
- Construction and Architecture:
In construction, calculating the perimeter of triangular plots or sections is crucial for determining the amount of materials needed for fencing, flooring, or other structural elements. For instance, if a triangular garden plot needs to be enclosed, knowing the perimeter helps in purchasing the correct length of fencing material.
- Landscaping:
Landscapers often deal with triangular sections of land. Knowing the perimeter allows them to estimate the resources required for edging, pathways, or decorative borders. This is essential for budgeting and efficient resource management.
- Navigation and Surveying:
In navigation, especially in maritime contexts, calculating the perimeter of triangular navigational paths can help in determining distances covered. Surveyors use perimeter calculations to measure land plots accurately, ensuring proper land usage and legal compliance.
- Art and Design:
Artists and designers often create triangular designs in various projects. Calculating the perimeter helps in framing these designs appropriately or in planning the layout of decorative elements around triangular shapes.
- Sports Fields:
In sports, particularly in designing fields or tracks, knowing the perimeter of triangular sections can assist in laying out tracks, field boundaries, or marking zones accurately. This ensures that the dimensions are in accordance with official standards.
Steps for Applying Perimeter Calculations in Real-World Problems
- Identify the Triangle Type:
Determine whether the triangle is equilateral, isosceles, or scalene. This helps in applying the correct formula for calculating the perimeter.
- Measure All Sides:
Accurately measure the lengths of all three sides of the triangle. Use appropriate tools like measuring tapes or laser distance meters for precise measurements.
- Apply the Perimeter Formula:
Use the formula \( P = a + b + c \) where \( P \) is the perimeter, and \( a \), \( b \), and \( c \) are the lengths of the sides. For specific types of triangles:
- Equilateral Triangle: \( P = 3a \)
- Isosceles Triangle: \( P = 2a + b \) where \( a \) is the length of the equal sides and \( b \) is the base.
- Convert Units if Necessary:
If the problem requires the perimeter in different units (e.g., from meters to feet), convert the units accordingly using conversion factors.
- Document and Utilize the Perimeter:
Record the calculated perimeter and use this information in further planning, material estimation, or any other relevant applications.
By following these steps, one can effectively use perimeter calculations in various real-world problems, ensuring accuracy and efficiency in practical applications.
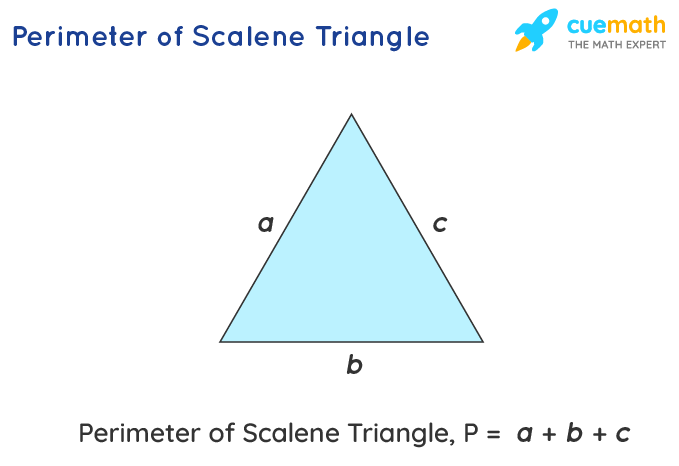
Common Mistakes and How to Avoid Them
Calculating the perimeter of a triangle might seem straightforward, but several common mistakes can lead to incorrect results. Here are some of these mistakes and tips on how to avoid them:
-
Incorrect Addition of Side Lengths:
Ensure all side lengths are added correctly. The order of addition does not matter, but all sides must be included once.
Example:
For a triangle with sides \(a = 5\), \(b = 7\), and \(c = 10\):
\[ \text{Perimeter} = a + b + c = 5 + 7 + 10 = 22 \]
-
Mixing Up Units:
Ensure all side lengths are in the same units before adding them. Convert any differing units to a common unit.
Example:
For sides \(a = 3\) meters, \(b = 150\) centimeters, and \(c = 2\) meters:
Convert all to meters:
\[ b = 150 \text{ cm} = 1.5 \text{ m} \]
\[ \text{Perimeter} = 3 + 1.5 + 2 = 6.5 \text{ meters} \]
-
Confusing Perimeter with Area:
Remember, perimeter measures the distance around the triangle (one-dimensional), while area measures the space inside it (two-dimensional).
-
Omitting a Side:
Ensure that all three sides are included in the calculation.
Example:
For a triangle with sides \(a = 8\), \(b = 6\), and \(c = 7\):
\[ \text{Perimeter} = 8 + 6 + 7 = 21 \]
-
Incorrect Use of Formulas:
For specific types of triangles, use the correct formula:
- Equilateral Triangle: \[ \text{Perimeter} = 3a \]
- Isosceles Triangle: \[ \text{Perimeter} = 2a + b \]
- Right Triangle: Use Pythagorean theorem to find the missing side if needed, then add all sides.
By paying attention to these common pitfalls, you can ensure accurate calculations of triangle perimeters.
FAQs on Triangle Perimeter
Understanding the perimeter of a triangle can often raise several questions. Here are some frequently asked questions and their answers:
-
What is the perimeter of a triangle?
The perimeter of a triangle is the total length of its boundary, calculated by summing the lengths of all three sides of the triangle. If the sides are denoted as \(a\), \(b\), and \(c\), the formula is:
\[ P = a + b + c \]
-
How do you find the perimeter of an equilateral triangle?
An equilateral triangle has all three sides equal. If each side is \(a\), the perimeter is calculated as:
\[ P = 3a \]
-
What is the formula for the perimeter of an isosceles triangle?
An isosceles triangle has two sides of equal length. If the equal sides are \(a\) and the base is \(b\), the perimeter is:
\[ P = 2a + b \]
-
How to calculate the perimeter of a right-angled triangle?
In a right-angled triangle, the sides are the base (\(b\)), the height (\(p\)), and the hypotenuse (\(h\)). Using the Pythagorean theorem:
\[ h = \sqrt{b^2 + p^2} \]
Thus, the perimeter is:
\[ P = b + p + h \]
-
Can a triangle have the same area and perimeter?
Yes, in special cases. These triangles are called equable triangles, where the numerical value of the perimeter is equal to the area.
-
How to find the perimeter of a triangle with coordinates?
If the vertices of a triangle are given as coordinates in a plane, you can calculate the length of each side using the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Sum the lengths of all three sides to get the perimeter.
Conclusion and Summary
The perimeter of a triangle is a fundamental concept in geometry, representing the total length of the triangle's boundary. Calculating the perimeter is straightforward and involves summing the lengths of all three sides. This can be expressed with the formula:
\( P = a + b + c \)
where \( P \) is the perimeter and \( a \), \( b \), and \( c \) are the lengths of the triangle's sides.
For specific types of triangles, the formulas can be simplified:
- Equilateral Triangle: \( P = 3a \) (since all sides are equal)
- Isosceles Triangle: \( P = 2a + b \) (where \( a \) is the length of the equal sides)
- Scalene Triangle: \( P = a + b + c \) (all sides are different)
Understanding and applying these formulas correctly can help avoid common mistakes such as:
- Incorrectly identifying the side lengths
- Using incorrect units or not converting units properly
- Misinterpreting the type of triangle and applying the wrong formula
The concept of perimeter extends beyond simple calculations. It is crucial in various real-world applications, from architectural design to land surveying, where accurate measurements are essential. Practicing with different types of triangles and real-world scenarios will strengthen your understanding and proficiency in calculating perimeters.
In summary, mastering the calculation of a triangle's perimeter involves:
- Identifying the type of triangle
- Using the correct formula based on the triangle's type
- Ensuring all measurements are accurate and in the same unit
With practice and attention to detail, you can confidently and accurately calculate the perimeter of any triangle, aiding in both academic and practical pursuits. Keep exploring and applying these concepts to become more adept in geometry.
Video hướng dẫn cách tìm chu vi tam giác. Thích hợp cho những ai đang tìm hiểu về chu vi của tam giác.
Cách Tìm Chu Vi Tam Giác | Toán Học với Thầy J
READ MORE:
Video hướng dẫn cách tìm chu vi của tam giác. Thích hợp cho những ai đang tìm hiểu về chu vi của tam giác.
Cách Tìm Chu Vi Của Tam Giác