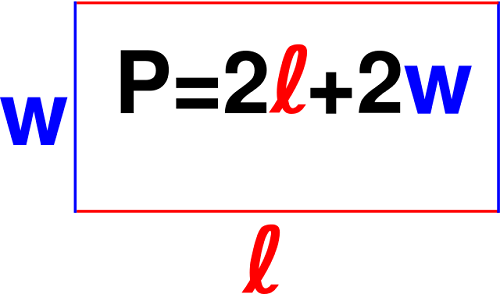Topic octagon perimeter: Understanding the perimeter of an octagon is crucial for various practical applications in geometry, architecture, and design. This guide will help you master the calculation of the octagon perimeter, explore its properties, and see real-world examples. Whether for academic purposes or practical use, this article provides a comprehensive overview of octagon perimeter calculations.
Table of Content
- Understanding the Perimeter of an Octagon
- Introduction to Octagon Geometry
- Definition and Properties of an Octagon
- Formulas for Octagon Perimeter and Area
- Derivation of Octagon Formulas
- Calculating Perimeter of a Regular Octagon
- Examples of Perimeter Calculations
- Area of an Octagon: Formula and Examples
- Circumcircle and Incircle of an Octagon
- Applications of Octagon Calculations
- Practice Problems on Octagon Perimeter and Area
- Frequently Asked Questions about Octagons
- Using Online Octagon Calculators
- YOUTUBE:
Understanding the Perimeter of an Octagon
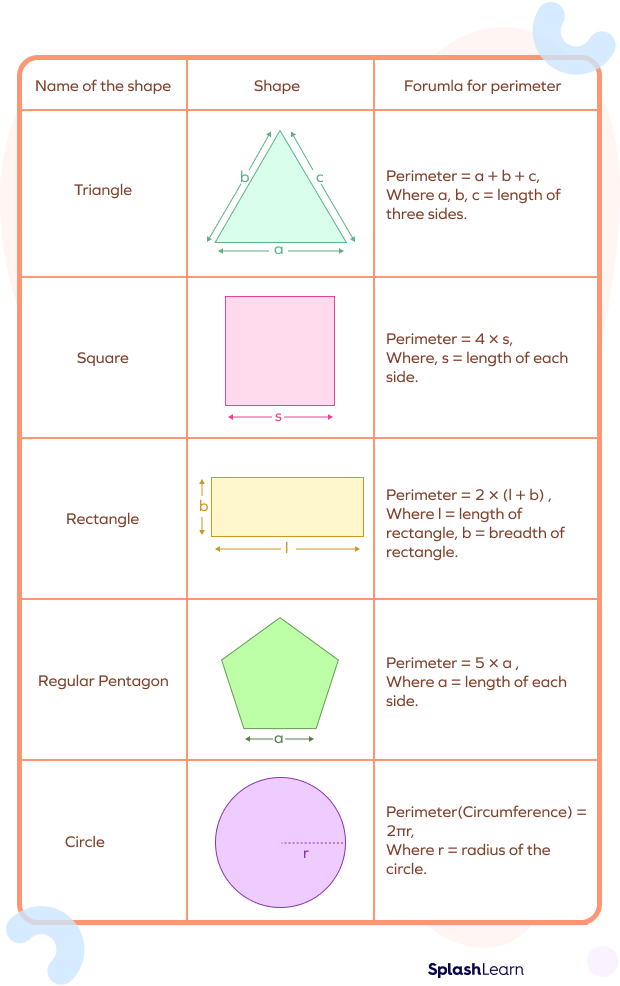
An octagon is an eight-sided polygon with equal sides and angles in the case of a regular octagon. Calculating its perimeter is straightforward and involves multiplying the length of one side by 8.
Formula for the Perimeter of a Regular Octagon
The perimeter \(P\) of a regular octagon can be calculated using the formula:
\[ P = 8a \]
where \(a\) is the length of one side of the octagon.
Example Calculation
If the length of one side of a regular octagon is 5 units, the perimeter is calculated as follows:
\[ P = 8 \times 5 = 40 \, \text{units} \]
This means that a fence of 40 units in length would be needed to enclose the entire octagonal area.
Distinguishing Perimeter from Area
It is important to differentiate between perimeter and area. While the perimeter measures the distance around the outside of the shape, the area refers to the space enclosed within the shape. Understanding this distinction is essential in mathematical problem-solving.
Applications of Perimeter Calculation
- Construction: Knowing the perimeter helps in determining how much fencing is required.
- Art and Design: Understanding perimeter aids in creating aesthetically pleasing compositions.
- Mathematics Education: It helps develop problem-solving skills, spatial reasoning, and a deeper understanding of geometric concepts.
Properties of a Regular Octagon
- Eight equal sides and angles.
- Each interior angle is 135°.
- Total sum of interior angles is 1080°.
- Each exterior angle is 45°.
- Total sum of exterior angles is 360°.
Mathematical Expressions Involving Octagons
Using trigonometric constants, the circumradius (\(R_c\)) and inradius (\(R_i\)) of a regular octagon can be calculated as:
\[ R_c = \frac{a}{\sqrt{2 - \sqrt{2}}} \]
\[ R_i = \frac{a}{2\sqrt{2} - 2} \]
Area of an Octagon
The area (\(A\)) of a regular octagon can be calculated using the formula:
\[ A = 2(1 + \sqrt{2})a^2 \]
For example, if each side of the octagon is 15 cm, the area is calculated as:
\[ A = 2(1 + \sqrt{2}) \times 15^2 = 1086.4 \, \text{cm}^2 \]
Conclusion
Understanding how to calculate the perimeter and area of an octagon is fundamental in various fields including construction, art, and mathematics education. These calculations are straightforward but essential for practical applications.
READ MORE:
Introduction to Octagon Geometry
An octagon is a polygon with eight sides and eight angles. Octagons can be regular, with all sides and angles equal, or irregular, with sides and angles of different lengths. Understanding octagon geometry involves exploring their properties, types, and the calculations related to their perimeter and area.
- An octagon has 8 sides and 8 angles.
- The sum of the interior angles of an octagon is \(1080^\circ\).
- The sum of the exterior angles is always \(360^\circ\).
Regular octagons have equal sides and angles. Each interior angle in a regular octagon measures \(135^\circ\), while each exterior angle measures \(45^\circ\). In an irregular octagon, the sides and angles are not equal but the properties of the angles summing to \(1080^\circ\) and exterior angles summing to \(360^\circ\) still hold.
| Property | Regular Octagon | Irregular Octagon |
| Sides | Equal | Unequal |
| Angles | Equal | Unequal |
| Diagonals | 20 | 20 |
| Interior Angle Sum | 1080° | 1080° |
| Exterior Angle Sum | 360° | 360° |
Understanding these properties helps in various applications of octagons in geometry and real-world contexts such as architecture and design.
Definition and Properties of an Octagon
An octagon is a polygon with eight sides, eight angles, and eight vertices. Octagons can be classified into regular and irregular types. A regular octagon has all sides and angles equal, while an irregular octagon has sides and angles of different lengths and measures. Octagons can also be convex or concave. A convex octagon has no interior angle greater than 180°, whereas a concave octagon has at least one interior angle greater than 180°.
- The sum of all interior angles in an octagon is \(1080^\circ\).
- The sum of all exterior angles is \(360^\circ\).
- A regular octagon has interior angles of \(135^\circ\) each.
- A regular octagon has exterior angles of \(45^\circ\) each.
- An octagon has 20 diagonals.
The perimeter of an octagon depends on whether it is regular or irregular. For a regular octagon, the perimeter (P) is calculated as:
\[ P = 8a \]
where \( a \) is the length of a side. For an irregular octagon, the perimeter is the sum of all side lengths.
The area (A) of a regular octagon with side length \( s \) can be calculated using the formula:
\[ A = 2(1+\sqrt{2})s^2 \]
In a regular octagon, symmetry is a significant property. It has 8 lines of symmetry and rotational symmetry of order 8, meaning it can be rotated 45° at a time and still appear the same.
Octagons are found in various real-life applications, such as stop signs and architectural designs, and have cultural significance representing concepts like rebirth and infinity.
Formulas for Octagon Perimeter and Area
Understanding the perimeter and area of an octagon is essential for various geometric applications. This section outlines the key formulas used to calculate these properties for both regular and irregular octagons.
Perimeter of a Regular Octagon
The perimeter of a regular octagon, where all sides are of equal length, is calculated using the formula:
\( P = 8a \)
where \( a \) is the length of one side.
Perimeter of an Irregular Octagon
For an irregular octagon, the perimeter is simply the sum of the lengths of all its sides:
\( P = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 \)
Area of a Regular Octagon
The area of a regular octagon can be found using the formula:
\( A = 2a^2(1 + \sqrt{2}) \)
where \( a \) is the length of one side. This formula is derived from dividing the octagon into 8 isosceles triangles and summing their areas.
Example Calculations
- Example 1: Find the perimeter of a regular octagon with side length 5 units.
\( P = 8 \times 5 = 40 \) units - Example 2: Find the area of a regular octagon with side length 5 units.
\( A = 2 \times 5^2(1 + \sqrt{2}) = 50(1 + \sqrt{2}) \approx 120.71 \) square units
Area of an Irregular Octagon
For an irregular octagon, the area is calculated by dividing it into simpler shapes (such as triangles and rectangles), finding the area of each shape, and summing them. There is no single formula for the area of an irregular octagon.
Derivation of Octagon Formulas
In this section, we will derive the formulas for the perimeter and area of a regular octagon. A regular octagon has all sides of equal length and all interior angles equal.
Perimeter of a Regular Octagon
The perimeter \(P\) of a regular octagon is simply the sum of the lengths of its eight equal sides. If each side has length \(s\), the formula for the perimeter is:
\[ P = 8s \]
Area of a Regular Octagon
The area \(A\) of a regular octagon can be derived using the formula for the area of a regular polygon:
\[ A = \frac{1}{2} \times Perimeter \times Apothem \]
For a regular octagon, the apothem \(a\) can be calculated using the formula:
\[ a = \frac{s}{2 \tan(\pi/8)} \]
Substituting the perimeter and apothem into the area formula, we get:
\[ A = \frac{1}{2} \times 8s \times \frac{s}{2 \tan(\pi/8)} = 2s^2 \cot(\pi/8) \]
Detailed Derivation
Step 1: Calculate the Perimeter
For a regular octagon with side length \(s\), the perimeter is:
\[ P = 8s \]
Step 2: Calculate the Apothem
The apothem of a regular octagon, which is the distance from the center to the midpoint of a side, is given by:
\[ a = \frac{s}{2 \tan(\pi/8)} \]
Step 3: Derive the Area
Using the general formula for the area of a regular polygon:
\[ A = \frac{1}{2} \times Perimeter \times Apothem \]
Substitute the perimeter and apothem of the octagon:
\[ A = \frac{1}{2} \times 8s \times \frac{s}{2 \tan(\pi/8)} \]
Simplify the expression:
\[ A = 2s^2 \cot(\pi/8) \]
Summary
The formulas for the perimeter and area of a regular octagon are:
- Perimeter: \( P = 8s \)
- Area: \( A = 2s^2 \cot(\pi/8) \)

Calculating Perimeter of a Regular Octagon
To calculate the perimeter of a regular octagon, we use a straightforward formula based on the length of its sides. A regular octagon has all eight sides of equal length.
The formula for the perimeter \( P \) of a regular octagon is given by:
\[ P = 8a \]
where \( a \) is the length of one side of the octagon.
Step-by-Step Calculation
- Measure the length of one side of the octagon. Let's denote this length as \( a \).
- Multiply the length of the side by 8 to find the perimeter:
\[ P = 8 \times a \]
For example, if each side of the octagon measures 5 units, the perimeter \( P \) would be calculated as:
\[ P = 8 \times 5 = 40 \text{ units} \]
Example Calculation
Consider a regular octagon with a side length of 10 cm. The perimeter can be calculated as follows:
- Side length (\( a \)) = 10 cm
- Number of sides = 8
- Perimeter (\( P \)) = 8 × 10 cm = 80 cm
Thus, the perimeter of the octagon is 80 cm.
Practice Problems
- Find the perimeter of a regular octagon with a side length of 7 units.
- A regular octagon has a perimeter of 64 units. What is the length of one side?
By following these steps and using the formula, you can easily calculate the perimeter of any regular octagon.
Examples of Perimeter Calculations
Calculating the perimeter of a regular octagon involves summing up the lengths of all its sides. For a regular octagon, since all sides are of equal length, the perimeter (P) is given by the formula:
Example 1
Find the perimeter of a regular octagon with each side measuring 4 units.
- Identify the side length:
a = 4 units. - Apply the perimeter formula:
P = 8a - Substitute the side length into the formula:
P = 8 \times 4 - Calculate the result:
P = 32 units.
Example 2
An octagonal garden has a side length of 6 meters. Determine its perimeter.
- Given side length:
a = 6 meters. - Use the perimeter formula:
P = 8a - Substitute the given length:
P = 8 \times 6 - Compute the perimeter:
P = 48 meters.
Example 3
A regular octagonal tile has a perimeter of 56 cm. Calculate the length of one side.
- Given perimeter:
P = 56 cm. - Use the perimeter formula:
P = 8a - Rearrange to find the side length:
a = \frac{P}{8} - Substitute the perimeter value:
a = \frac{56}{8} - Calculate the side length:
a = 7 cm.
Example 4
The side of a regular octagonal table is 3.5 feet. What is its perimeter?
- Side length:
a = 3.5 feet. - Apply the perimeter formula:
P = 8a - Insert the side length into the formula:
P = 8 \times 3.5 - Find the perimeter:
P = 28 feet.
These examples illustrate how to calculate the perimeter of a regular octagon by simply multiplying the side length by 8.
Area of an Octagon: Formula and Examples
The area of an octagon is the amount of space enclosed within its eight sides. There are various formulas to calculate the area depending on the information available, such as side length, apothem, or radius. Let's explore these formulas and some examples in detail.
Formula Using Side Length
The formula to calculate the area of a regular octagon using its side length \( a \) is:
\[
\text{Area} = 2a^2 (1 + \sqrt{2})
\]
Example:
Find the area of a regular octagon with a side length of 5 units.
Solution:
\[
\text{Area} = 2 \times 5^2 \times (1 + \sqrt{2}) \\
= 2 \times 25 \times (1 + 1.414) \\
= 50 \times 2.414 \\
= 120.7 \text{ square units}
\]
Formula Using Apothem and Perimeter
The formula to calculate the area of a regular octagon using the apothem \( a \) and the perimeter \( P \) is:
\[
\text{Area} = \frac{1}{2} \times P \times a
\]
Example:
Find the area of a regular octagon with a perimeter of 128 units and an apothem of 12 units.
Solution:
\[
\text{Area} = \frac{1}{2} \times 128 \times 12 \\
= 64 \times 12 \\
= 768 \text{ square units}
\]
Formula Using Radius
The formula to calculate the area of a regular octagon using the radius \( r \) (distance from the center to a vertex) is:
\[
\text{Area} = 2 \sqrt{2} r^2
\]
Example:
Find the area of a regular octagon with a radius of 12.5 units.
Solution:
\[
\text{Area} = 2 \sqrt{2} \times (12.5)^2 \\
= 2 \times 1.414 \times 156.25 \\
= 2 \times 220.97 \\
= 441.94 \text{ square units}
\]
Area of an Irregular Octagon
For irregular octagons, the area cannot be calculated using a single formula. Instead, the octagon is divided into simpler shapes (such as triangles), and the area of each shape is calculated and then summed up.
Example:
Find the area of an irregular octagon by dividing it into triangles and using Heron's formula for each triangle.
This process involves calculating the semi-perimeter and then using it to find the area of each triangle formed within the octagon.
By understanding these formulas and examples, one can effectively calculate the area of both regular and irregular octagons.
Circumcircle and Incircle of an Octagon
The circumcircle and incircle are two important circles associated with a regular octagon. These circles help in understanding various geometric properties and relationships within the octagon.
Circumcircle
The circumcircle of a regular octagon is a circle that passes through all eight vertices of the octagon. The center of this circle is known as the circumcenter, and the radius is called the circumradius.
To find the circumradius \( R \) of a regular octagon with side length \( a \), use the formula:
\[ R = \frac{a}{2} \csc\left(\frac{\pi}{8}\right) \]
Where \( \csc \) is the cosecant function.
The steps to draw a circumcircle around a regular octagon are:
- Identify the center of the octagon, which is the point of intersection of the diagonals.
- Measure the distance from the center to any vertex of the octagon; this distance is the circumradius.
- Using a compass set to the circumradius, draw a circle with the center as the center of the octagon. This circle will pass through all the vertices of the octagon.
Incircle
The incircle of a regular octagon is a circle inscribed within the octagon, tangent to all eight sides. The center of this circle is known as the incenter, and the radius is called the inradius.
To find the inradius \( r \) of a regular octagon with side length \( a \), use the formula:
\[ r = \frac{a}{2} \cot\left(\frac{\pi}{8}\right) \]
Where \( \cot \) is the cotangent function.
The steps to draw an incircle inside a regular octagon are:
- Identify the center of the octagon, which is the point of intersection of the angle bisectors.
- Measure the perpendicular distance from the center to any side of the octagon; this distance is the inradius.
- Using a compass set to the inradius, draw a circle with the center as the center of the octagon. This circle will be tangent to all the sides of the octagon.
These geometric properties and constructions of the circumcircle and incircle are fundamental in understanding the structure and symmetries of a regular octagon.

Applications of Octagon Calculations
Octagon calculations have a variety of applications in different fields. Here are some key areas where they are particularly useful:
- Architecture and Design:
In architecture, octagonal shapes are frequently used in the design of buildings, particularly for decorative elements such as domes, towers, and floor plans. Calculating the perimeter and area of octagons is essential for accurate construction and material estimation.
- Urban Planning:
Octagonal shapes are often employed in urban planning, especially for roundabouts, pavements, and parks. Understanding the geometric properties of octagons helps in optimizing space and ensuring aesthetic appeal.
- Engineering:
In engineering, octagonal cross-sections are used in structures like pylons, columns, and beams to distribute stress evenly and enhance stability. Calculations related to octagons ensure structural integrity and safety.
- Mathematics Education:
Octagons are a fundamental part of geometry education. Problems involving octagon perimeter and area calculations help students develop spatial reasoning and problem-solving skills.
- Art and Culture:
Octagons appear in various art forms, including mosaics, tiling patterns, and religious symbols. Accurate geometric calculations enable artists to create symmetrical and visually appealing designs.
- Product Design:
Many products, from tiles to coasters, incorporate octagonal shapes. Knowing how to calculate the area and perimeter of octagons helps designers create functional and aesthetically pleasing products.
- Games and Recreational Activities:
Octagons are used in the design of board games, playgrounds, and sports arenas. Understanding octagonal geometry is crucial for creating balanced and engaging recreational spaces.
Overall, octagon calculations play a significant role in various professional and academic fields, highlighting the importance of mastering these geometric concepts.
Practice Problems on Octagon Perimeter and Area
Here are some practice problems to help you master the calculations of the perimeter and area of a regular octagon. Use the formulas for the perimeter \( P = 8a \) and the area \( A = 2(1 + \sqrt{2})a^2 \), where \( a \) is the length of a side.
-
Find the perimeter of a regular octagon with a side length of 6 cm.
Solution:
- Perimeter formula: \( P = 8a \)
- Given side length: \( a = 6 \) cm
- Calculation: \( P = 8 \times 6 = 48 \) cm
- Answer: The perimeter is 48 cm.
-
Calculate the area of a regular octagon with a side length of 5 inches.
Solution:
- Area formula: \( A = 2(1 + \sqrt{2})a^2 \)
- Given side length: \( a = 5 \) inches
- Calculation: \[ A = 2(1 + \sqrt{2}) \times 5^2 \] \[ A = 2(1 + \sqrt{2}) \times 25 \] \[ A = 2(1 + 1.414) \times 25 \] \[ A = 2 \times 2.414 \times 25 \] \[ A = 120.7 \text{ square inches} \]
- Answer: The area is 120.7 square inches.
-
If the perimeter of a regular octagon is 64 meters, find the length of one side.
Solution:
- Perimeter formula: \( P = 8a \)
- Given perimeter: \( P = 64 \) meters
- Calculation: \[ 64 = 8a \] \[ a = \frac{64}{8} \] \[ a = 8 \text{ meters} \]
- Answer: The length of one side is 8 meters.
-
Determine the area of a regular octagon with a side length of 7 feet.
Solution:
- Area formula: \( A = 2(1 + \sqrt{2})a^2 \)
- Given side length: \( a = 7 \) feet
- Calculation: \[ A = 2(1 + \sqrt{2}) \times 7^2 \] \[ A = 2(1 + \sqrt{2}) \times 49 \] \[ A = 2(1 + 1.414) \times 49 \] \[ A = 2 \times 2.414 \times 49 \] \[ A = 236.7 \text{ square feet} \]
- Answer: The area is 236.7 square feet.
-
Find the side length of a regular octagon if its area is 482.84 square yards.
Solution:
- Area formula: \( A = 2(1 + \sqrt{2})a^2 \)
- Given area: \( A = 482.84 \) square yards
- Calculation: \[ 482.84 = 2(1 + \sqrt{2})a^2 \] \[ 482.84 = 2(1 + 1.414)a^2 \] \[ 482.84 = 2 \times 2.414a^2 \] \[ 482.84 = 4.828a^2 \] \[ a^2 = \frac{482.84}{4.828} \] \[ a^2 = 100 \] \[ a = \sqrt{100} \] \[ a = 10 \text{ yards} \]
- Answer: The side length is 10 yards.
Frequently Asked Questions about Octagons
We understand that diving into the details of octagons can raise many questions. Below are some frequently asked questions and their answers to help you understand octagons better.
-
What are the properties of an octagon?
An octagon has 8 sides and 8 angles. For a regular octagon, all sides and angles are equal. The sum of the interior angles is 1080 degrees, and each interior angle in a regular octagon measures 135 degrees. The sum of the exterior angles is 360 degrees, with each exterior angle measuring 45 degrees.
-
How do you calculate the perimeter of a regular octagon?
The perimeter of a regular octagon can be calculated using the formula:
\[ P = 8a \]
where \( a \) is the length of one side.
-
Can you multiply an octagon's sides by 8 to get the perimeter?
Yes, but only for a regular octagon. In an irregular octagon, the sides may have different lengths, so you need to add the lengths of all sides individually to find the perimeter.
-
What is the formula for the area of a regular octagon?
The formula for the area of a regular octagon is:
\[ A = 2a^2(1 + \sqrt{2}) \]
where \( a \) is the length of one side.
-
What's the difference between a regular and an irregular octagon?
A regular octagon has all sides and angles equal, whereas an irregular octagon does not have equal sides and angles.
-
What are some real-world examples of octagons?
Common examples include stop signs, which are usually regular octagons, and some types of umbrellas. Octagonal shapes are also seen in various designs and architectural elements.
-
How many diagonals does an octagon have?
An octagon has 20 diagonals.
These FAQs cover some of the essential aspects of octagons. Understanding these properties and formulas will help you in various geometrical calculations and real-world applications.
Using Online Octagon Calculators
Online octagon calculators are valuable tools for quickly determining the perimeter and area of an octagon without manual calculations. Here is a guide on how to use these calculators effectively:
Steps to Use an Online Octagon Calculator
-
Open an online octagon calculator. Several options are available, such as those offered by BYJU'S and Cuemath.
-
Locate the input field where you will enter the length of a side of the octagon.
-
Enter the side length. For example, if each side of the octagon is 5 units, type "5" into the input field.
-
Click the "Calculate" button. The calculator will use the formulas to compute the perimeter and area of the octagon.
-
View the results displayed on the screen. The perimeter and area will be shown in their respective units.
Example Calculations Using Online Tools
-
Example 1: If the side length is 8 units:
- Perimeter: \( 8 \times 8 = 64 \, \text{units} \)
- Area: \( 2 \times 8^2 \times (1 + \sqrt{2}) = 309.02 \, \text{square units} \)
-
Example 2: If the side length is 7 units:
- Perimeter: \( 8 \times 7 = 56 \, \text{units} \)
- Area: \( 2 \times 7^2 \times (1 + \sqrt{2}) = 236.57 \, \text{square units} \)
-
Example 3: If the side length is 11 units:
- Perimeter: \( 8 \times 11 = 88 \, \text{units} \)
- Area: \( 2 \times 11^2 \times (1 + \sqrt{2}) = 584.19 \, \text{square units} \)
Benefits of Using Online Calculators
Accuracy: Ensures precise calculations for both perimeter and area.
Speed: Delivers instant results, saving time compared to manual calculations.
Convenience: Easy to use and accessible from any device with internet access.
Using online octagon calculators streamlines the process of finding the perimeter and area, making it easier for students, teachers, and professionals to obtain accurate results quickly.
Cách Tính Chu Vi Bát Giác
READ MORE:
Hướng dẫn cách tính chu vi của một đa giác bát giác đều. Bạn sẽ tìm hiểu cách tính chu vi của hình bát giác và áp dụng cho các bài toán thực tế.
Hướng dẫn tính chu vi đa giác bát giác