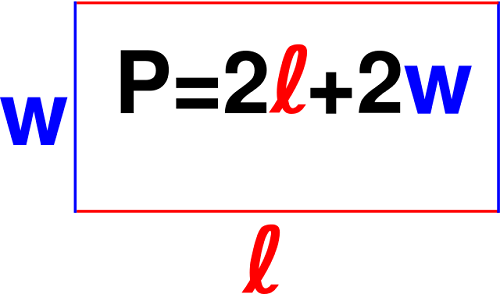Topic perimeter math: Perimeter math involves finding the total length around a two-dimensional shape. This concept is crucial in various fields, from geometry to real-world applications like construction and design. In this article, we'll explore formulas and examples to make calculating perimeters easy and intuitive.
Table of Content
- Understanding Perimeter in Mathematics
- Introduction to Perimeter
- Basic Perimeter Formulas
- Perimeter of Different Shapes
- Perimeter of a Rectangle
- Perimeter of a Square
- Perimeter of a Triangle
- Perimeter of a Circle
- Perimeter of a Parallelogram
- Perimeter of a Trapezoid
- Perimeter of an Ellipse
- Special Cases and Examples
- Finding Perimeter with Missing Side Lengths
- Perimeter Word Problems
- Comparing Area and Perimeter
- Practical Applications of Perimeter
- Using Perimeter in Real-Life Scenarios
- Common Mistakes and How to Avoid Them
- Advanced Topics in Perimeter
- YOUTUBE: Xem video về chu vi trong toán học để hiểu rõ hơn về khái niệm này và áp dụng vào thực tế.
Understanding Perimeter in Mathematics
The perimeter of a shape is the total length of its boundary. It is a fundamental concept in geometry, often used in various real-life applications such as construction, crafting, and land measurement.
Formulas for Common Shapes
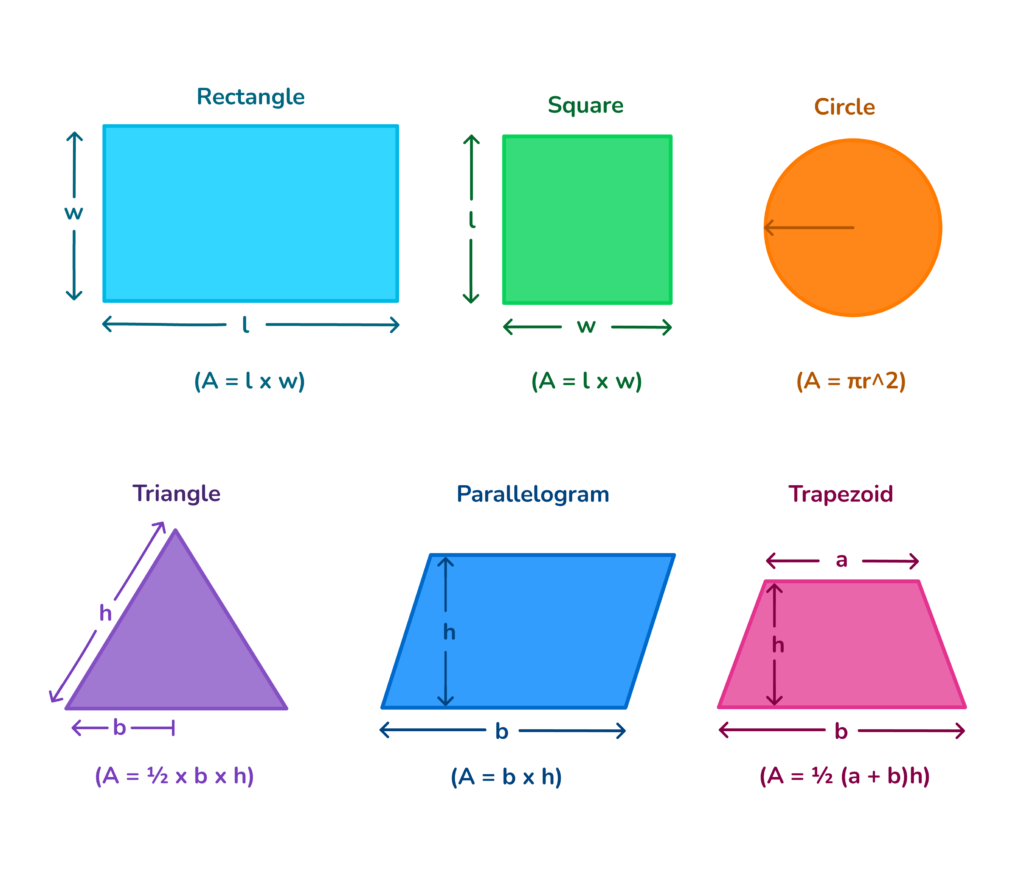
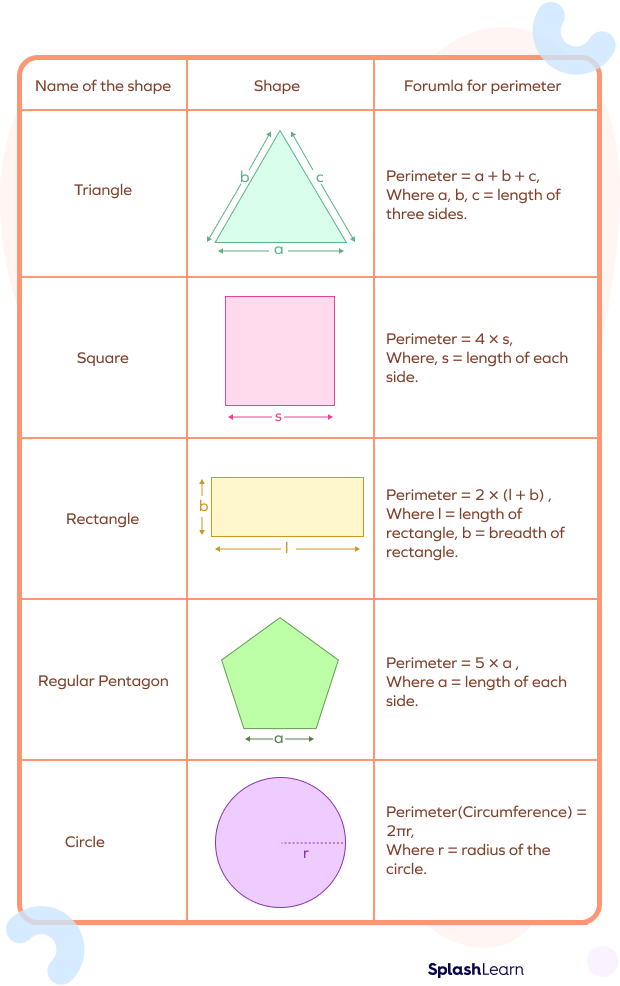
- Square: The perimeter of a square with side length \( s \) is calculated as \( P = 4s \).
- Rectangle: The perimeter of a rectangle with length \( l \) and width \( w \) is given by \( P = 2l + 2w \).
- Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter is \( P = a + b + c \).
- Circle: The perimeter of a circle, also known as the circumference, with radius \( r \) is \( P = 2\pi r \).
Calculating Perimeter
To find the perimeter of various shapes, apply the relevant formula and sum the lengths of all sides. Here are a few examples:
- Square Example: If the side length of a square is 5 units, its perimeter is \( P = 4 \times 5 = 20 \) units.
- Rectangle Example: For a rectangle with a length of 10 units and a width of 4 units, the perimeter is \( P = 2 \times 10 + 2 \times 4 = 28 \) units.
- Triangle Example: Given a triangle with sides of 3 units, 4 units, and 5 units, the perimeter is \( P = 3 + 4 + 5 = 12 \) units.
- Circle Example: For a circle with a radius of 7 units, the perimeter (circumference) is \( P = 2 \times \pi \times 7 = 44 \) units (using \( \pi \approx 3.14 \)).
Applications of Perimeter
Perimeter is used in various practical scenarios:
- Construction: Determining the amount of material needed to build fences, walls, and other structures.
- Crafting: Calculating the length of trim or lace required for decorating objects.
- Land Measurement: Assessing the boundary length of properties for land division and legal purposes.
Practice Problems
Here are some problems to practice calculating the perimeter:
| Shape | Dimensions | Perimeter Formula | Perimeter |
| Square | Side = 8 units | \( P = 4s \) | \( 4 \times 8 = 32 \) units |
| Rectangle | Length = 15 units, Width = 10 units | \( P = 2l + 2w \) | \( 2 \times 15 + 2 \times 10 = 50 \) units |
| Triangle | Sides = 6 units, 8 units, 10 units | \( P = a + b + c \) | \( 6 + 8 + 10 = 24 \) units |
| Circle | Radius = 5 units | \( P = 2\pi r \) | \( 2 \times 3.14 \times 5 = 31.4 \) units |
Understanding the concept of perimeter and practicing its calculation with different shapes will enhance your problem-solving skills in mathematics.
READ MORE:
Introduction to Perimeter
Perimeter is a fundamental concept in mathematics that refers to the total distance around the outside of a shape. It is a crucial measurement used in various fields such as geometry, engineering, architecture, and more.
Understanding perimeter is essential for accurately determining the length of boundaries, fences, or any other closed figure. Whether you're working with basic shapes like squares and rectangles or more complex polygons, knowing how to calculate perimeter is vital.
By mastering the concept of perimeter, you'll be equipped to solve a wide range of mathematical problems and real-world scenarios. Let's delve deeper into the basics of perimeter and explore its significance in mathematics and everyday life.
Basic Perimeter Formulas
The perimeter of a shape is the total length of its boundary. It can be calculated by summing the lengths of all the sides. Here are the basic perimeter formulas for common geometric shapes:
-
Perimeter of a Rectangle
Formula: \( P = 2(l + w) \)
where \( l \) is the length and \( w \) is the width of the rectangle.
-
Perimeter of a Square
Formula: \( P = 4s \)
where \( s \) is the side length of the square.
-
Perimeter of a Triangle
Formula: \( P = a + b + c \)
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle.
-
Perimeter of a Circle (Circumference)
Formula: \( P = 2\pi r \) or \( P = \pi d \)
where \( r \) is the radius and \( d \) is the diameter of the circle.
-
Perimeter of a Parallelogram
Formula: \( P = 2(a + b) \)
where \( a \) and \( b \) are the lengths of the adjacent sides of the parallelogram.
-
Perimeter of a Trapezoid
Formula: \( P = a + b + c + d \)
where \( a \), \( b \), \( c \), and \( d \) are the lengths of the sides of the trapezoid.
-
Perimeter of an Ellipse (Approximation)
Formula: \( P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \)
where \( a \) and \( b \) are the semi-major and semi-minor axes of the ellipse, respectively.
Perimeter of Different Shapes
The perimeter of a shape is the total distance around the edges of the shape. Here are the formulas to calculate the perimeter for various common shapes:
Square
For a square with side length \( s \), the perimeter \( P \) is calculated as:
\[ P = 4s \]
Rectangle
For a rectangle with length \( l \) and width \( w \), the perimeter \( P \) is calculated as:
\[ P = 2l + 2w \]
Equilateral Triangle
For an equilateral triangle with side length \( s \), the perimeter \( P \) is calculated as:
\[ P = 3s \]
Regular Polygon
For a regular \( n \)-sided polygon with side length \( s \), the perimeter \( P \) is calculated as:
\[ P = ns \]
Circle
For a circle with radius \( r \), the perimeter (circumference) \( C \) is calculated as:
\[ C = 2\pi r \]
Parallelogram
For a parallelogram with side lengths \( a \) and \( b \), the perimeter \( P \) is calculated as:
\[ P = 2a + 2b \]
Trapezoid
For a trapezoid with side lengths \( a \), \( b \), \( c \), and \( d \), the perimeter \( P \) is calculated as:
\[ P = a + b + c + d \]
Ellipse
For an ellipse with semi-major axis \( a \) and semi-minor axis \( b \), an approximate formula for the perimeter \( P \) is:
\[ P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \]
These formulas help in determining the perimeter of various shapes, which is useful in many real-life applications like fencing a yard, framing a picture, or decorating a room.
Perimeter of a Rectangle
The perimeter of a rectangle is the total distance around the outside of the rectangle. It is calculated by adding together the lengths of all four sides. Since opposite sides of a rectangle are equal, the formula simplifies to:
\( P = 2L + 2W \)
where \( P \) is the perimeter, \( L \) is the length, and \( W \) is the width.
Step-by-Step Calculation
- Measure the length and width of the rectangle.
- Double the length and double the width.
- Add these two values together to get the perimeter.
Examples
- Example 1: Find the perimeter of a rectangle with a length of 10 cm and a width of 5 cm.
\( P = 2(10) + 2(5) = 20 + 10 = 30 \) cm
- Example 2: A rectangle has a length of 8 meters and a width of 3 meters. Calculate its perimeter.
\( P = 2(8) + 2(3) = 16 + 6 = 22 \) meters
Finding a Missing Dimension
If the perimeter and one dimension are known, the missing dimension can be calculated:
- Finding the Length:
\( L = \frac{P}{2} - W \)
- Finding the Width:
\( W = \frac{P}{2} - L \)
For example, if a rectangle has a perimeter of 50 cm and a width of 10 cm:
\( L = \frac{50}{2} - 10 = 25 - 10 = 15 \) cm
Real-Life Applications
The perimeter of a rectangle can be used in various practical scenarios such as:
- Calculating the amount of fencing required to enclose a rectangular garden.
- Determining the length of trim needed to border a rectangular picture frame.
- Estimating the ribbon length required to decorate the edges of a rectangular tablecloth.

Perimeter of a Square
The perimeter of a square is the total length of all its sides. Since all sides of a square are equal, the perimeter can be calculated using a simple formula. Below, we will explain the formula, provide some examples, and show how to calculate the perimeter in different scenarios.
Formula for the Perimeter of a Square
The formula to calculate the perimeter of a square is:
\[ P = 4 \times \text{side} \]
where \( P \) is the perimeter and \(\text{side}\) is the length of one side of the square.
Step-by-Step Calculation
- Measure the length of one side of the square.
- Multiply the length of the side by 4.
- The result is the perimeter of the square.
Examples
- If the side length of a square is 5 units, the perimeter is:
\[ P = 4 \times 5 = 20 \text{ units} \]
- If the perimeter of a square is 36 units, to find the side length:
\[ \text{side} = \frac{P}{4} = \frac{36}{4} = 9 \text{ units} \]
Finding Perimeter When Area is Given
If the area of a square is given, we can find the side length and then calculate the perimeter. The steps are:
- Find the side length using the area formula: \[ \text{side} = \sqrt{\text{Area}} \]
- Multiply the side length by 4 to find the perimeter.
Example: If the area is 49 square units:
- Calculate the side length: \[ \text{side} = \sqrt{49} = 7 \text{ units} \]
- Then calculate the perimeter: \[ P = 4 \times 7 = 28 \text{ units} \]
Finding Perimeter When Diagonal is Given
When the diagonal of a square is given, the side length can be found using the relationship between the side and the diagonal:
\[ \text{side} = \frac{\text{diagonal}}{\sqrt{2}} \]
Then, the perimeter can be calculated as usual. Example:
- If the diagonal is 10 units:
\[ \text{side} = \frac{10}{\sqrt{2}} = 5\sqrt{2} \text{ units} \]
Then the perimeter is:
\[ P = 4 \times 5\sqrt{2} = 20\sqrt{2} \text{ units} \]
Practical Application
Understanding how to calculate the perimeter of a square is useful in various real-life situations, such as determining the length of the fencing needed to enclose a square garden or the amount of material required to frame a square picture.
Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle. It is calculated by adding the lengths of all three sides of the triangle. Here are the basic formulas for finding the perimeter of different types of triangles:
General Formula
For any triangle with side lengths \( a \), \( b \), and \( c \), the perimeter \( P \) is given by:
\[ P = a + b + c \]
Equilateral Triangle
An equilateral triangle has three equal sides. If each side has length \( a \), the perimeter \( P \) is:
\[ P = 3a \]
For example, if each side of an equilateral triangle is 6 units, the perimeter is:
\[ P = 3 \times 6 = 18 \, \text{units} \]
Isosceles Triangle
An isosceles triangle has two equal sides. If the equal sides have length \( a \) and the base has length \( b \), the perimeter \( P \) is:
\[ P = 2a + b \]
For example, if the equal sides are 10 units each and the base is 15 units, the perimeter is:
\[ P = 2 \times 10 + 15 = 35 \, \text{units} \]
Scalene Triangle
A scalene triangle has all sides of different lengths. For side lengths \( a \), \( b \), and \( c \), the perimeter \( P \) is:
\[ P = a + b + c \]
For example, if the sides are 5 units, 7 units, and 8 units, the perimeter is:
\[ P = 5 + 7 + 8 = 20 \, \text{units} \]
Right Triangle
A right triangle has one angle of 90 degrees. The sides are known as the legs \( a \) and \( b \), and the hypotenuse \( c \). The hypotenuse can be calculated using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Then, the perimeter \( P \) is:
\[ P = a + b + c \]
For example, if the legs are 6 units and 8 units, the hypotenuse is:
\[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{units} \]
The perimeter is:
\[ P = 6 + 8 + 10 = 24 \, \text{units} \]
By understanding these formulas, you can easily calculate the perimeter of any triangle given the lengths of its sides.
Perimeter of a Circle
The perimeter of a circle is more commonly referred to as the circumference. It is the total distance around the circle. To calculate the circumference, you need to know either the radius or the diameter of the circle. Here are the key formulas:
- When the radius (r) is known:
The formula for the circumference is given by:
\[ C = 2\pi r \]
where \( \pi \) (pi) is approximately 3.14159.
- When the diameter (d) is known:
The formula for the circumference is given by:
\[ C = \pi d \]
Note that the diameter is twice the radius, i.e., \( d = 2r \).
- When the area (A) of the circle is known:
The formula to find the circumference can be derived from the area formula:
\[ C = 2\pi \sqrt{\frac{A}{\pi}} \]
Example Calculations
Let's go through a couple of examples to illustrate how to use these formulas.
- Example 1: Given a radius of 5 cm, find the circumference.
- Using the formula \( C = 2\pi r \):
- \[ C = 2 \times 3.14159 \times 5 \]
- \[ C \approx 31.4159 \, \text{cm} \]
- Example 2: Given a diameter of 10 cm, find the circumference.
- Using the formula \( C = \pi d \):
- \[ C = 3.14159 \times 10 \]
- \[ C \approx 31.4159 \, \text{cm} \]
- Example 3: Given an area of 78.5 cm², find the circumference.
- First, find the radius using the area formula \( A = \pi r^2 \):
- \[ r = \sqrt{\frac{A}{\pi}} = \sqrt{\frac{78.5}{3.14159}} \approx 5 \, \text{cm} \]
- Then, use the radius to find the circumference:
- \[ C = 2\pi r = 2 \times 3.14159 \times 5 \]
- \[ C \approx 31.4159 \, \text{cm} \]
Understanding the perimeter (circumference) of a circle is essential in various fields, from geometry to real-life applications such as calculating the distance around circular objects.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the total distance around the shape. It is calculated by summing the lengths of all four sides. Since a parallelogram has opposite sides that are equal in length, the formula for the perimeter is straightforward.
The formula for the perimeter \( P \) of a parallelogram is given by:
\[ P = 2(a + b) \]
where \( a \) and \( b \) are the lengths of the two adjacent sides of the parallelogram.
To better understand this, let's break it down step-by-step:
- Identify the lengths of the two adjacent sides of the parallelogram. Let's call these lengths \( a \) and \( b \).
- Sum these two lengths: \( a + b \).
- Multiply the result by 2 to account for both pairs of equal sides: \( 2(a + b) \).
Here are a few examples to illustrate the concept:
| Example | Side \( a \) (cm) | Side \( b \) (cm) | Perimeter (cm) |
|---|---|---|---|
| 1 | 12 | 6 | \( 2(12 + 6) = 2 \times 18 = 36 \) |
| 2 | 5 | 10 | \( 2(5 + 10) = 2 \times 15 = 30 \) |
| 3 | 8 | 7 | \( 2(8 + 7) = 2 \times 15 = 30 \) |
By following these steps and using the formula, you can easily calculate the perimeter of any parallelogram given the lengths of its adjacent sides.

Perimeter of a Trapezoid
The perimeter of a trapezoid is the total distance around its four sides. A trapezoid is a quadrilateral with only one pair of parallel sides. To calculate the perimeter, you sum the lengths of all four sides.
Formula
The formula for the perimeter of a trapezoid is:
\[ P = a + b + c + d \]
where \( a \) and \( b \) are the lengths of the parallel sides (bases), and \( c \) and \( d \) are the lengths of the non-parallel sides (legs).
Steps to Calculate Perimeter
- Identify the lengths of all four sides of the trapezoid.
- Substitute these lengths into the formula.
- Add the lengths together to find the perimeter.
Examples
Example 1: Find the perimeter of a trapezoid with side lengths 10 cm, 8 cm, 6 cm, and 12 cm.
- Given: \( a = 10 \) cm, \( b = 8 \) cm, \( c = 6 \) cm, \( d = 12 \) cm
- Using the formula: \[ P = 10 + 8 + 6 + 12 \]
- Calculation: \[ P = 36 \text{ cm} \]
- So, the perimeter of the trapezoid is 36 cm.
Example 2: A trapezoid has bases of 15 m and 25 m, and legs of 10 m each. Find its perimeter.
- Given: \( a = 15 \) m, \( b = 25 \) m, \( c = 10 \) m, \( d = 10 \) m
- Using the formula: \[ P = 15 + 25 + 10 + 10 \]
- Calculation: \[ P = 60 \text{ m} \]
- So, the perimeter of the trapezoid is 60 m.
Perimeter of an Ellipse
The perimeter of an ellipse is not as straightforward to calculate as the perimeter of other shapes like rectangles or circles. There is no simple formula for the exact perimeter of an ellipse, but an approximation can be made using the following formula:
\[ P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \]
Here, \( a \) is the length of the semi-major axis, and \( b \) is the length of the semi-minor axis. This formula provides a good approximation for the perimeter.
Steps to Calculate the Perimeter of an Ellipse
- Identify the lengths of the semi-major axis (\( a \)) and the semi-minor axis (\( b \)).
- Square both the semi-major axis and the semi-minor axis: \( a^2 \) and \( b^2 \).
- Add the squared values: \( a^2 + b^2 \).
- Divide the sum by 2: \( \frac{a^2 + b^2}{2} \).
- Take the square root of the result: \( \sqrt{\frac{a^2 + b^2}{2}} \).
- Multiply by \( 2\pi \) to approximate the perimeter: \( P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \).
Example Calculation
Consider an ellipse with a semi-major axis \( a \) of 5 units and a semi-minor axis \( b \) of 3 units:
- Square the lengths: \( 5^2 = 25 \) and \( 3^2 = 9 \).
- Add the squared values: \( 25 + 9 = 34 \).
- Divide by 2: \( \frac{34}{2} = 17 \).
- Take the square root: \( \sqrt{17} \approx 4.123 \).
- Multiply by \( 2\pi \): \( 2\pi \times 4.123 \approx 25.92 \).
Thus, the approximate perimeter of the ellipse is 25.92 units.
Advanced Calculation
For more precise calculations, especially for ellipses with a high eccentricity, specialized elliptical perimeter calculators or numerical integration methods can be used. However, for most practical purposes, the approximation given above is sufficiently accurate.
Fun Facts
- An ellipse can be thought of as a stretched circle.
- The sum of the distances from any point on the ellipse to its two foci is constant.
- Ellipses are often found in nature, such as the orbits of planets and the shape of some fruits.
Special Cases and Examples
Understanding the perimeter of different shapes can involve various special cases and practical examples. Here, we explore some interesting scenarios and solve problems step by step to demonstrate these concepts clearly.
Special Cases
- Perimeter with Missing Side Lengths: When one or more side lengths are missing, use known properties and relationships of the shape to find the missing lengths.
- Using Ratios: For shapes where the sides are in a given ratio, use the ratio to express unknown side lengths in terms of a single variable and solve for the perimeter.
- Shapes with Curved Sides: For shapes like circles or ellipses, the concept of perimeter extends to circumference, which may require specific formulas.
Examples
-
Example 1: Rectangle with Missing Side Length
Given a rectangle where the length \( l \) is known to be 10 units and the perimeter \( P \) is 36 units, find the width \( w \).
Using the perimeter formula for a rectangle:
\( P = 2(l + w) \)
Substitute the known values:
\( 36 = 2(10 + w) \)
Solve for \( w \):
\( 36 = 20 + 2w \)
\( 16 = 2w \)
\( w = 8 \) units
-
Example 2: Perimeter of a Trapezoid
Calculate the perimeter of a trapezoid with sides 5 cm, 7 cm, 8 cm, and 10 cm.
Using the perimeter formula for a trapezoid:
\( P = a + b + c + d \)
Substitute the side lengths:
\( P = 5 + 7 + 8 + 10 = 30 \) cm
-
Example 3: Equilateral Triangle
If the perimeter of an equilateral triangle is 45 units, find the length of each side.
Using the perimeter formula for an equilateral triangle:
\( P = 3a \)
Substitute the known perimeter:
\( 45 = 3a \)
Solve for \( a \):
\( a = 15 \) units
These examples illustrate the application of perimeter formulas to solve real-world problems, highlighting the importance of understanding perimeter calculations.
Finding Perimeter with Missing Side Lengths
When calculating the perimeter of a shape, sometimes you may encounter situations where one or more side lengths are missing. Here’s a step-by-step guide to finding the missing side lengths using the given perimeter:
Step-by-Step Process
- Understand the Perimeter Formula: The perimeter is the total distance around the shape. For different shapes, the formulas are:
- Square: \(P = 4 \times L\), where \(L\) is the length of one side.
- Rectangle: \(P = 2 \times (l + w)\), where \(l\) is the length and \(w\) is the width.
- Triangle: \(P = a + b + c\), where \(a\), \(b\), and \(c\) are the lengths of the sides.
- Parallelogram: \(P = 2 \times (a + b)\), where \(a\) and \(b\) are the lengths of adjacent sides.
- Trapezoid: \(P = a + b + c + d\), where \(a\), \(b\), \(c\), and \(d\) are the lengths of the sides.
- Sum Known Side Lengths: Add up the lengths of the sides that are known.
- Subtract from Total Perimeter: Subtract the sum of the known side lengths from the total perimeter to find the length of the missing side(s).
Examples
Here are some practical examples:
Example 1: Rectangle
Given a rectangle with a perimeter of 50 units, and one side length is 14 units. Find the missing width.
- Perimeter formula: \(P = 2 \times (l + w)\)
- Plug in the known values: \(50 = 2 \times (14 + w)\)
- Simplify: \(50 = 28 + 2w\)
- Solve for \(w\): \(2w = 22 \Rightarrow w = 11\)
The missing width is 11 units.
Example 2: Triangle
Given a triangle with a perimeter of 24 units and two side lengths of 7 units and 5 units. Find the length of the third side.
- Perimeter formula: \(P = a + b + c\)
- Plug in the known values: \(24 = 7 + 5 + c\)
- Simplify: \(24 = 12 + c\)
- Solve for \(c\): \(c = 12\)
The length of the third side is 12 units.
Practice Problems
- A square has a perimeter of 36 units. Find the length of one side.
- A parallelogram has a perimeter of 40 units. If one side length is 12 units, find the length of the adjacent side.
Using these steps and understanding the perimeter formulas for various shapes, you can easily find the missing side lengths when given the total perimeter.

Perimeter Word Problems
Perimeter word problems help students apply their understanding of perimeter to real-world scenarios. These problems can involve various shapes, including rectangles, squares, triangles, and circles. Here are some examples and step-by-step solutions to help you understand how to approach these problems.
Example 1: Perimeter of a Rectangle
Problem: A garden is twice as long as it is wide. If the perimeter of the garden is 36 meters, what are the length and width of the garden?
- Let the width be \( w \) meters.
- Then the length is \( 2w \) meters.
- The perimeter of a rectangle is given by \( 2 \times (\text{length} + \text{width}) \).
- So, \( 2 \times (w + 2w) = 36 \).
- Simplify the equation: \( 2 \times 3w = 36 \).
- Divide both sides by 2: \( 3w = 18 \).
- Solve for \( w \): \( w = 6 \) meters.
- The length is \( 2w = 12 \) meters.
- Therefore, the width is 6 meters and the length is 12 meters.
Example 2: Perimeter of a Triangle
Problem: A triangle has sides of 7 cm, 10 cm, and 5 cm. What is the perimeter of the triangle?
- The perimeter of a triangle is the sum of the lengths of its sides.
- Add the side lengths: \( 7 + 10 + 5 \).
- Simplify: \( 7 + 10 + 5 = 22 \) cm.
- Therefore, the perimeter of the triangle is 22 cm.
Example 3: Perimeter of a Circle (Circumference)
Problem: A circular garden has a diameter of 10 meters. What is the perimeter (circumference) of the garden?
- The perimeter (circumference) of a circle is given by \( \pi \times \text{diameter} \).
- So, \( \text{Circumference} = \pi \times 10 \).
- Using \( \pi \approx 3.14 \), the circumference is \( 3.14 \times 10 = 31.4 \) meters.
- Therefore, the perimeter of the circular garden is approximately 31.4 meters.
Example 4: Real-Life Application
Problem: A rectangular playground is 30 meters long and 20 meters wide. A fence is to be built around the playground. How much fencing material is needed?
- The perimeter of a rectangle is given by \( 2 \times (\text{length} + \text{width}) \).
- So, \( \text{Perimeter} = 2 \times (30 + 20) \).
- Simplify: \( \text{Perimeter} = 2 \times 50 = 100 \) meters.
- Therefore, 100 meters of fencing material is needed.
Example 5: Word Problem with Missing Side Lengths
Problem: The perimeter of a rectangular field is 64 meters. The length is 6 meters more than the width. Find the dimensions of the field.
- Let the width be \( w \) meters.
- Then the length is \( w + 6 \) meters.
- The perimeter of a rectangle is given by \( 2 \times (\text{length} + \text{width}) \).
- So, \( 2 \times (w + (w + 6)) = 64 \).
- Simplify the equation: \( 2 \times (2w + 6) = 64 \).
- Divide both sides by 2: \( 2w + 6 = 32 \).
- Subtract 6 from both sides: \( 2w = 26 \).
- Solve for \( w \): \( w = 13 \) meters.
- The length is \( w + 6 = 19 \) meters.
- Therefore, the width is 13 meters and the length is 19 meters.
Comparing Area and Perimeter
Understanding the differences and relationships between area and perimeter is essential in mathematics, especially when analyzing shapes and solving real-world problems. Here's a comprehensive guide to help you compare these two fundamental concepts.
Definitions
- Perimeter: The perimeter of a shape is the total length of its boundary. It is measured in linear units such as meters, centimeters, or feet.
- Area: The area of a shape is the amount of space it covers. It is measured in square units such as square meters, square centimeters, or square feet.
Formulas
| Shape | Perimeter Formula | Area Formula |
|---|---|---|
| Square | 4 × side | side × side |
| Rectangle | 2 × (length + width) | length × width |
| Circle | 2πr | πr2 |
Comparison
Although both area and perimeter measure different properties of a shape, they are related in various ways. Here are some key points to consider:
- Shapes with the same perimeter can have different areas. For example, a rectangle and a square can have the same perimeter but different areas.
- Shapes with the same area can have different perimeters. For instance, a long, narrow rectangle and a more square-like rectangle can have the same area but different perimeters.
- The perimeter is always a linear measurement, while the area is always a square measurement.
Examples
Consider the following examples to illustrate the differences and similarities:
Example 1: Rectangle
Let's compare two rectangles:
- Rectangle A: length = 10 units, width = 5 units
- Rectangle B: length = 8 units, width = 7 units
For Rectangle A:
- Perimeter = 2 × (10 + 5) = 30 units
- Area = 10 × 5 = 50 square units
For Rectangle B:
- Perimeter = 2 × (8 + 7) = 30 units
- Area = 8 × 7 = 56 square units
Although both rectangles have the same perimeter, their areas are different.
Example 2: Square and Rectangle
Consider a square and a rectangle with the same area:
- Square: side = 6 units
- Rectangle: length = 9 units, width = 4 units
For the square:
- Perimeter = 4 × 6 = 24 units
- Area = 6 × 6 = 36 square units
For the rectangle:
- Perimeter = 2 × (9 + 4) = 26 units
- Area = 9 × 4 = 36 square units
In this case, both shapes have the same area, but different perimeters.
Visual Comparison
Visual aids can help in understanding the relationship between area and perimeter. For example, drawing shapes with the same area but different perimeters, or vice versa, can illustrate these concepts effectively.
Conclusion
Understanding the distinction and relationship between area and perimeter is crucial for solving various mathematical problems and real-life applications. Remember, the perimeter measures the boundary length of a shape, while the area measures the space it covers. Both concepts are fundamental in geometry and essential for various practical applications.
Practical Applications of Perimeter
The concept of perimeter is widely used in various real-life scenarios. Understanding how to calculate and apply perimeter can be beneficial in numerous practical situations:
- Construction and Landscaping: When planning the construction of a building, a fence, or a garden, knowing the perimeter helps determine the amount of materials needed. For example, to build a fence around a garden, you need to calculate the total length of the boundary to purchase the right amount of fencing material.
- Home Improvement: Projects such as installing baseboards, crown molding, or wallpaper require accurate measurements of a room's perimeter to ensure you purchase enough materials. For instance, if a room is 15 feet long and 10 feet wide, the perimeter would be \(2 \times (15 + 10) = 50\) feet.
- Gardening: To keep animals out of a garden, you need to know the perimeter to buy the right length of fencing. A rectangular garden measuring 20 feet by 30 feet would have a perimeter of \(2 \times (20 + 30) = 100\) feet.
- Art and Framing: When creating frames for pictures or artworks, the perimeter helps determine how much framing material is required. For example, a picture frame for an 8-inch by 10-inch photo has a perimeter of \(2 \times (8 + 10) = 36\) inches.
- Roads and Bridges: Engineers use perimeter calculations in the planning and construction of roads and bridges to ensure proper design and material usage.
- Real Estate and Property Surveying: Perimeter measurements are crucial in property surveys to define boundaries and to calculate the length of fencing needed to enclose a property.
These examples illustrate how understanding perimeter is essential in planning, designing, and executing various tasks efficiently and accurately.
Using Perimeter in Real-Life Scenarios
Understanding the concept of perimeter is crucial not just in mathematical problems, but also in various real-life situations. Below are some practical applications of perimeter:
-
Fencing a Property:
One of the most common applications of perimeter is in determining the amount of fencing material needed to enclose a yard or garden. To calculate this, measure the length of all sides of the area you want to fence and sum them up.
- Measure the length of each side of the yard.
- Use the formula for the perimeter of a rectangle: \( P = 2l + 2w \) where \( l \) is the length and \( w \) is the width.
- Add the lengths of all sides for irregular shapes.
-
Framing Pictures:
When framing a picture, knowing the perimeter helps determine the length of the frame material required. Measure the sides of the picture and calculate the perimeter to ensure you purchase the correct amount of framing material.
- Measure the dimensions of the picture.
- For a rectangular picture, use \( P = 2l + 2w \).
- For a circular picture frame, use the formula \( P = 2\pi r \), where \( r \) is the radius.
-
Building and Construction:
In construction, perimeter calculations are vital for determining the boundaries of properties, areas for flooring, and lengths of materials needed for building edges.
- Measure the dimensions of the construction area.
- Apply the relevant perimeter formulas based on the shape of the area (rectangular, triangular, etc.).
- Sum up the lengths to find the total perimeter for ordering materials.
-
Landscaping:
For landscaping projects, such as creating garden beds or pathways, knowing the perimeter helps in planning and purchasing the right amount of materials.
- Outline the shape of the garden bed or pathway.
- Measure each segment if the shape is irregular.
- Add the lengths to find the total perimeter.
These applications illustrate the importance of understanding and calculating perimeter in various practical contexts, ensuring efficient use of materials and accurate project planning.
Common Mistakes and How to Avoid Them
Understanding common mistakes in calculating the perimeter and learning how to avoid them can significantly improve accuracy in solving perimeter-related problems. Here are some frequent errors and tips to overcome them:
-
Incorrect Formula Usage:
One common mistake is using the wrong formula for different shapes. For example, using the formula for the perimeter of a square instead of a rectangle.
- Solution: Always ensure you use the correct formula. For a rectangle, use \(P = 2 \times (L + W)\) where \(L\) is the length and \(W\) is the width.
-
Misidentifying Shape Sides:
Confusing the lengths of sides in various shapes, such as treating all sides as equal in a rectangle.
- Solution: Clearly identify and label all sides. In a rectangle, opposite sides are equal, so calculate accordingly.
-
Units Mismatch:
Mixing different units (e.g., centimeters and meters) without proper conversion.
- Solution: Always convert all measurements to the same unit before performing calculations.
-
Neglecting All Sides:
Forgetting to include all sides of the shape in the calculation, particularly in irregular shapes.
- Solution: Double-check that all sides are accounted for by listing each one and summing them up.
-
Confusing Perimeter with Area:
Mixing up the concepts of perimeter and area, leading to incorrect applications of formulas.
- Solution: Remember that the perimeter is the total length around the shape while the area measures the surface inside the shape.
-
Errors in Complex Shapes:
Making mistakes in calculating the perimeter of shapes with multiple sides or irregular shapes.
- Solution: Break down complex shapes into simpler parts, calculate the perimeter of each part, and then sum them up.
By being aware of these common mistakes and following these solutions, students can improve their accuracy and understanding when calculating the perimeter of various shapes.
Advanced Topics in Perimeter
As we delve deeper into the concept of perimeter, we encounter more complex and interesting applications. Understanding these advanced topics can help in solving real-world problems and enhancing mathematical skills.
Perimeter in Coordinate Geometry
In coordinate geometry, the perimeter of a shape can be calculated by determining the distances between points on a coordinate plane. For example, to find the perimeter of a polygon, you sum the distances between consecutive vertices.
Given points \((x_1, y_1)\), \((x_2, y_2)\), ..., \((x_n, y_n)\), the distance between two points \((x_i, y_i)\) and \((x_{i+1}, y_{i+1})\) is calculated using the distance formula:
\[
d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2}
\]
The perimeter \(P\) of the polygon is the sum of these distances:
\[
P = \sum_{i=1}^{n} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2}
\]
Perimeter of Complex Shapes
For complex shapes, especially those not composed of straight lines, the perimeter calculation involves integral calculus. This is common in determining the perimeter of curves or irregular shapes.
For instance, the perimeter of an ellipse can be approximated using Ramanujan's formula:
\[
P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]
\]
where \(a\) and \(b\) are the semi-major and semi-minor axes of the ellipse, respectively.
Using Parametric Equations
Another advanced method involves using parametric equations. If a curve is described parametrically by \(x(t)\) and \(y(t)\) for \(t \in [a, b]\), the perimeter \(P\) can be found using:
\[
P = \int_{a}^{b} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \, dt
\]
This technique is particularly useful for finding the perimeters of curves such as cycloids and epicycloids.
Applications in Engineering and Design
Understanding advanced perimeter calculations is crucial in various fields such as engineering and architectural design. For example, determining the perimeter is essential when designing roads, bridges, and even in land surveying. Accurate calculations ensure that materials are used efficiently and structures are built correctly.
Software Tools and Simulation
Today, many software tools can assist in perimeter calculations, especially for complex shapes. Programs like AutoCAD, MATLAB, and various online calculators can handle these advanced computations, providing accurate results quickly and efficiently.
Conclusion
Mastering advanced topics in perimeter not only enhances mathematical understanding but also provides practical skills applicable in many professional fields. Whether through coordinate geometry, parametric equations, or software tools, these methods open up new possibilities for solving complex problems.
Xem video về chu vi trong toán học để hiểu rõ hơn về khái niệm này và áp dụng vào thực tế.
Video: Math Antics - Chu vi (Perimeter)
READ MORE:
Xem video về cách tính chu vi để nắm rõ khái niệm và áp dụng vào các bài toán thực tế cùng thầy J.
Video: Tìm chu vi | Toán cùng thầy J