Topic hexagon perimeter: The perimeter of a hexagon is a fundamental geometric concept that is essential in various fields of mathematics and engineering. Whether dealing with regular or irregular hexagons, knowing how to calculate their perimeter is crucial. This article will guide you through the formulas, examples, and applications to master the concept of hexagon perimeter efficiently.
Table of Content
- Hexagon Perimeter
- Introduction to Hexagons
- Definition and Properties of Hexagons
- Types of Hexagons
- Regular Hexagon
- Irregular Hexagon
- Formulas for Hexagon Perimeter
- Regular Hexagon Perimeter Formula
- Irregular Hexagon Perimeter Calculation
- Examples and Solved Problems
- Applications of Hexagons
- Hexagons in Real Life
- YOUTUBE: Video hướng dẫn lớp 7 về cách tính chu vi của hình lục giác. Tìm hiểu các công thức và ví dụ minh họa về chu vi của hình lục giác trong bài giảng này.
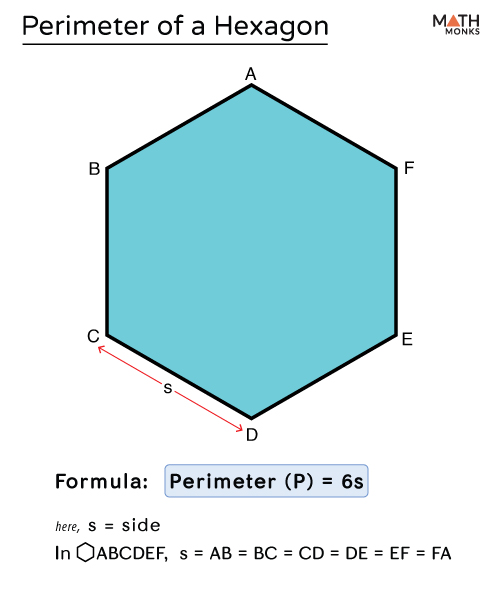
Hexagon Perimeter
The perimeter of a hexagon is the total length of its six sides. Hexagons can be regular, with all sides and angles equal, or irregular, with sides and angles of different measures.
Formula for Regular Hexagon Perimeter
For a regular hexagon (where all sides are equal in length), the perimeter (P) is calculated using the formula:
\[
P = 6s
\]
where \( s \) is the length of one side of the hexagon.
Example:
- Given a regular hexagon with a side length of 5 cm:
- Perimeter = \( 6 \times 5 \) cm = 30 cm
Formula for Irregular Hexagon Perimeter
For an irregular hexagon, the perimeter is the sum of the lengths of all six sides:
\[
P = s_1 + s_2 + s_3 + s_4 + s_5 + s_6
\]
where \( s_1, s_2, s_3, s_4, s_5, \) and \( s_6 \) are the lengths of the sides.
Example:
- Given an irregular hexagon with sides measuring 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, and 9 cm:
- Perimeter = \( 4 + 5 + 6 + 7 + 8 + 9 \) cm = 39 cm
Properties of a Regular Hexagon
- It has 6 equal sides and 6 equal angles.
- The sum of interior angles is 720°.
- Each interior angle is 120° and each exterior angle is 60°.
- It can be divided into 6 equilateral triangles.
- It has 6 lines of symmetry.
Real-Life Examples of Hexagons
Hexagons are commonly found in nature and human-made structures:
- Honeycombs in beehives
- Tiles and mosaics
- Nut and bolt heads
- Certain game board designs

READ MORE:
Introduction to Hexagons
A hexagon is a six-sided polygon with a variety of intriguing properties and applications. This geometric shape is prevalent in both nature and human-made structures, offering a unique blend of aesthetic appeal and functional efficiency. In this section, we will explore the basic characteristics, types, and significance of hexagons.
- Definition: A hexagon is a two-dimensional polygon with six edges, six vertices, and six interior angles.
- Types of Hexagons:
- Regular Hexagon: All sides and interior angles are equal. Each interior angle measures 120 degrees, and the hexagon can be subdivided into six equilateral triangles.
- Irregular Hexagon: Sides and angles are not necessarily equal, leading to a variety of shapes and configurations.
- Convex Hexagon: All interior angles are less than 180 degrees, and vertices point outwards.
- Concave Hexagon: At least one interior angle is greater than 180 degrees, and some vertices point inward.
- Properties:
- Sum of interior angles: 720 degrees
- Number of diagonals: 9
- Symmetry: Regular hexagons have 6 lines of symmetry and rotational symmetry of order 6.
- Real-World Examples:
- Nature: Honeycombs, snowflakes
- Human-made: Tiles, nuts, and bolts
Understanding hexagons helps us appreciate their role in both mathematics and practical applications, from natural phenomena to engineering and design.
Definition and Properties of Hexagons
A hexagon is a polygon with six sides and six angles. Hexagons can be regular, with all sides and angles equal, or irregular, with sides and angles of different measures. Here are some key properties and definitions related to hexagons:
- All hexagons are two-dimensional closed figures with 6 edges, faces, and vertices.
- The sum of the internal angles of all hexagons is equal to 720°.
- Hexagons have 9 diagonals.
Regular Hexagon
A regular hexagon has six equal sides and six equal angles. It exhibits several distinct properties:
- All sides and interior angles are equal.
- The interior angles measure 120° each.
- The exterior angles measure 60° each.
- It has 6 lines of symmetry.
- A regular hexagon can be divided into 6 equilateral triangles.
The perimeter of a regular hexagon can be calculated using the formula:
\( P = 6 \times a \)
Where \( P \) is the perimeter and \( a \) is the side length.
Irregular Hexagon
An irregular hexagon has sides and angles that are not all equal. To find the perimeter of an irregular hexagon, you sum the lengths of all its sides. Depending on the given information, you might need to use various geometric formulas to find the side lengths.
Types of Hexagons
- Regular Hexagon: All sides and angles are equal.
- Irregular Hexagon: Sides and angles are not equal.
- Convex Hexagon: All interior angles are less than 180°.
- Concave Hexagon: At least one interior angle is greater than 180°.
Properties of Hexagons
- The sum of the interior angles of a hexagon is 720°.
- A regular hexagon has 6 equal sides and 6 equal angles of 120° each.
- Hexagons have 9 diagonals: 3 long diagonals and 6 short diagonals in a regular hexagon.
Types of Hexagons
Hexagons, six-sided polygons, come in various forms. Each type has unique properties and characteristics, and they are classified based on side lengths and internal angles. Below are the main types of hexagons:
- Regular Hexagon: All six sides and angles are equal. It is highly symmetrical and can be divided into six equilateral triangles.
- Irregular Hexagon: Sides and angles are not necessarily equal. This type lacks the symmetry of regular hexagons and can take various shapes.
- Convex Hexagon: All internal angles are less than 180 degrees, and vertices point outward. This includes regular hexagons and some irregular ones.
- Concave Hexagon: At least one internal angle is greater than 180 degrees, giving the hexagon a "caved-in" appearance at one or more vertices.
Understanding these types helps in various applications, from geometry studies to practical uses in design and architecture.
Regular Hexagon
A regular hexagon is a polygon with six equal sides and six equal angles. This shape is highly symmetrical, making it a common subject of study in geometry. Below are some key properties and calculations related to regular hexagons.
- All six sides are of equal length.
- All interior angles are 120 degrees.
- All exterior angles are 60 degrees.
- The sum of all interior angles is 720 degrees.
- It has six vertices and nine diagonals.
Area of a Regular Hexagon
The area \( A \) of a regular hexagon can be calculated using the formula:
$$ A = \frac{3 \sqrt{3}}{2} a^2 $$
where \( a \) is the length of one side of the hexagon.
Perimeter of a Regular Hexagon
The perimeter \( P \) of a regular hexagon is simply the total length of its six sides, which can be calculated using the formula:
$$ P = 6a $$
where \( a \) is the length of one side.
Examples
Example 1: Calculate the area and perimeter of a regular hexagon with side length 6 cm.
- Area: $$ A = \frac{3 \sqrt{3}}{2} (6)^2 = 93.53 \, \text{cm}^2 $$
- Perimeter: $$ P = 6 \times 6 = 36 \, \text{cm} $$
Example 2: If the perimeter of a regular hexagon is 48 cm, find the length of one side.
- Given \( P = 48 \, \text{cm} \), we have:
- $$ 48 = 6a $$
- $$ a = \frac{48}{6} = 8 \, \text{cm} $$
Regular hexagons are not only mathematically interesting but also appear frequently in nature and human design, such as in honeycombs, tiling patterns, and various architectural elements.

Irregular Hexagon
An irregular hexagon is a six-sided polygon where not all sides and angles are equal. Unlike a regular hexagon, which has equal sides and angles, the irregular hexagon has sides of different lengths and angles of different measures. This variability requires specific methods to calculate its properties such as perimeter and area.
To calculate the perimeter of an irregular hexagon, you need to sum the lengths of all its sides:
\[
\text{Perimeter} = a + b + c + d + e + f
\]
Where \(a, b, c, d, e,\) and \(f\) are the lengths of the six sides of the hexagon.
To determine the area of an irregular hexagon, you can divide it into simpler shapes like triangles and rectangles, calculate their areas separately, and then sum them up. For instance, using the triangulation method:
- Divide the hexagon into triangles by drawing diagonals from one vertex to all non-adjacent vertices.
- Calculate the area of each triangle using Heron's formula or the basic formula for triangles.
- Sum the areas of all the triangles to find the total area of the hexagon.
An example of calculating the perimeter of an irregular hexagon:
- If the sides of the hexagon are \(3 \, \text{cm}\), \(4 \, \text{cm}\), \(5 \, \text{cm}\), \(3 \, \text{cm}\), \(4 \, \text{cm}\), and \(5 \, \text{cm}\), the perimeter is calculated as:
\[
\text{Perimeter} = 3 + 4 + 5 + 3 + 4 + 5 = 24 \, \text{cm}
\]
Understanding the properties of irregular hexagons and the methods for calculating their perimeter and area is essential for various applications in geometry and practical scenarios such as construction and design.
Formulas for Hexagon Perimeter
The perimeter of a hexagon depends on whether it is regular or irregular. Here, we will discuss the formulas for both types of hexagons.
Regular Hexagon
A regular hexagon has all its sides of equal length. The formula for the perimeter \( P \) of a regular hexagon with side length \( s \) is:
\[ P = 6s \]
For example, if each side of a regular hexagon is 5 cm, the perimeter would be:
\[ P = 6 \times 5 = 30 \, \text{cm} \]
Irregular Hexagon
An irregular hexagon has sides of different lengths. The perimeter of an irregular hexagon is the sum of the lengths of all its sides. If the side lengths are \( a, b, c, d, e, \) and \( f \), then the perimeter \( P \) is:
\[ P = a + b + c + d + e + f \]
For example, if the side lengths of an irregular hexagon are 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, and 8 cm, the perimeter would be:
\[ P = 3 + 4 + 5 + 6 + 7 + 8 = 33 \, \text{cm} \]
Perimeter Given Diameter
For a regular hexagon, if the diameter (distance between two opposite vertices) is known, the side length can be found using trigonometric ratios. Once the side length is determined, the perimeter can be calculated using the regular hexagon formula.
Perimeter with Vertices
If the coordinates of the vertices of a hexagon are given, the length of each side can be calculated using the distance formula:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Summing the lengths of all sides gives the perimeter of the hexagon.
Regular Hexagon Perimeter Formula
A regular hexagon is a polygon with six equal sides and six equal angles. To calculate the perimeter of a regular hexagon, you can use the following formula:
\[
P = 6 \times a
\]
Where \( P \) is the perimeter and \( a \) is the length of one side of the hexagon.
Here is a step-by-step approach to calculating the perimeter of a regular hexagon:
- Identify the length of one side of the hexagon (denoted as \( a \)).
- Multiply this length by 6 to find the perimeter.
For example, if the side length \( a \) is 5 units, the perimeter \( P \) would be:
\[
P = 6 \times 5 = 30 \text{ units}
\]
This simple formula makes it easy to determine the total distance around the hexagon.
Below is a table summarizing the perimeter calculation for various side lengths:
| Side Length (a) | Perimeter (P) |
|---|---|
| 2 units | 12 units |
| 3 units | 18 units |
| 4 units | 24 units |
| 5 units | 30 units |
| 6 units | 36 units |
Understanding and applying this formula can help in solving various problems related to the perimeter of regular hexagons.
Irregular Hexagon Perimeter Calculation
An irregular hexagon is a six-sided polygon where not all sides and angles are equal. Calculating the perimeter of an irregular hexagon involves summing the lengths of all its sides. Follow the steps below for a detailed calculation process:
-
Measure Each Side: Determine the length of each of the six sides of the irregular hexagon. Label them as \(a_1, a_2, a_3, a_4, a_5,\) and \(a_6\). -
Add the Side Lengths: Sum the lengths of all six sides to find the perimeter.
\[
\text{Perimeter} = a_1 + a_2 + a_3 + a_4 + a_5 + a_6
\] -
Example Calculation: Assume the sides of an irregular hexagon are 5 cm, 7 cm, 4 cm, 6 cm, 8 cm, and 3 cm.- Side \(a_1 = 5 \, \text{cm}\)
- Side \(a_2 = 7 \, \text{cm}\)
- Side \(a_3 = 4 \, \text{cm}\)
- Side \(a_4 = 6 \, \text{cm}\)
- Side \(a_5 = 8 \, \text{cm}\)
- Side \(a_6 = 3 \, \text{cm}\)
Adding these lengths together:
\[
\text{Perimeter} = 5 + 7 + 4 + 6 + 8 + 3 = 33 \, \text{cm}
\]
This method ensures that you accurately calculate the perimeter of any irregular hexagon by simply summing the lengths of all its sides.
Examples and Solved Problems
Let's explore some examples and solved problems related to hexagon perimeter calculations. We'll cover both regular and irregular hexagons.
Example 1: Perimeter of a Regular Hexagon
Given a regular hexagon with a side length of 8 cm, calculate the perimeter.
Since all sides of a regular hexagon are equal, the perimeter \( P \) is given by:
\[ P = 6s \]
Where \( s \) is the side length.
Substitute the given side length:
\[ P = 6 \times 8 = 48 \text{ cm} \]
Thus, the perimeter of the hexagon is 48 cm.
Example 2: Perimeter of an Irregular Hexagon
Consider an irregular hexagon with side lengths of 5 cm, 7 cm, 6 cm, 4 cm, 8 cm, and 9 cm. Calculate the perimeter.
The perimeter \( P \) of an irregular hexagon is the sum of all its side lengths:
\[ P = 5 + 7 + 6 + 4 + 8 + 9 \]
Add the side lengths:
\[ P = 39 \text{ cm} \]
Therefore, the perimeter of the irregular hexagon is 39 cm.
Example 3: Hexagon with Given Vertices
Given the coordinates of the vertices of an irregular hexagon: \( A(1, 2) \), \( B(4, 2) \), \( C(5, 6) \), \( D(3, 8) \), \( E(1, 7) \), and \( F(0, 4) \). Calculate the perimeter using the distance formula.
The distance formula is given by:
\[ \overline{XY} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Calculate each side length:
- \[ \overline{AB} = \sqrt{(4-1)^2 + (2-2)^2} = \sqrt{9} = 3 \text{ units} \]
- \[ \overline{BC} = \sqrt{(5-4)^2 + (6-2)^2} = \sqrt{17} \text{ units} \]
- \[ \overline{CD} = \sqrt{(3-5)^2 + (8-6)^2} = \sqrt{8} \text{ units} \]
- \[ \overline{DE} = \sqrt{(1-3)^2 + (7-8)^2} = \sqrt{5} \text{ units} \]
- \[ \overline{EF} = \sqrt{(0-1)^2 + (4-7)^2} = \sqrt{10} \text{ units} \]
- \[ \overline{FA} = \sqrt{(1-0)^2 + (2-4)^2} = \sqrt{5} \text{ units} \]
Add all the side lengths to find the perimeter:
\[ P = 3 + \sqrt{17} + \sqrt{8} + \sqrt{5} + \sqrt{10} + \sqrt{5} \]
Calculate the sum:
\[ P \approx 3 + 4.12 + 2.83 + 2.24 + 3.16 + 2.24 = 17.59 \text{ units} \]
Thus, the perimeter of the hexagon is approximately 17.59 units.
Example 4: Perimeter of an Inscribed Hexagon
A hexagon is inscribed in a circle with a radius of 10 units. Calculate the perimeter.
For a regular hexagon inscribed in a circle, the side length \( s \) is equal to the radius \( r \) of the circle. Therefore, the perimeter \( P \) is given by:
\[ P = 6r \]
Substitute the radius:
\[ P = 6 \times 10 = 60 \text{ units} \]
Hence, the perimeter of the inscribed hexagon is 60 units.
Applications of Hexagons
Hexagons appear in various natural and human-made structures due to their unique properties. Their geometric efficiency and versatility make them valuable in numerous fields. Here are some notable applications of hexagons:
1. Natural World
- Honeycombs: Bees construct honeycombs with hexagonal cells to optimize space and material use, providing maximum storage with minimal wax.
- Crystals: Many crystals, including quartz, exhibit hexagonal symmetry, reflecting the efficient packing of atoms within their structure.
- Snowflakes: Snowflakes commonly form hexagonal shapes due to the molecular arrangement of water molecules during crystallization.
2. Engineering and Design
- Tiling: Hexagonal tiling provides a way to cover surfaces without gaps or overlaps, often used in flooring and wall designs.
- Structural Efficiency: Hexagonal shapes in engineering structures, such as grids or meshes, offer high strength-to-weight ratios, beneficial in aerospace and architectural designs.
- Carbon Nanotubes: The structure of carbon nanotubes features hexagonal arrangements of carbon atoms, contributing to their exceptional strength and electrical properties.
3. Technology
- Graphene: Graphene sheets are composed of a single layer of carbon atoms arranged in a hexagonal lattice, leading to its remarkable conductivity and strength.
- Hexagonal Pixels: Some digital imaging technologies use hexagonal pixels to increase resolution and reduce aliasing effects.
4. Board Games and Puzzles
- Settlers of Catan: The popular board game uses a hexagonal grid for its modular game board, enhancing strategic gameplay and variability.
- Hexagonal Puzzles: Puzzles with hexagonal pieces offer unique challenges and solutions compared to traditional square-based puzzles.
5. Chemical Compounds
- Aromatic Compounds: Many organic compounds, such as benzene, have hexagonal ring structures, influencing their chemical properties and reactivity.
- Ring Structures: Hexagonal rings are common in various chemical structures, contributing to the stability and behavior of molecules.
These examples demonstrate the hexagon's versatile application across different fields, illustrating its importance in both natural phenomena and technological innovations.
Hexagons in Real Life
Hexagons are a prominent shape in both natural and man-made environments due to their efficiency and aesthetic appeal. Here are some key examples of hexagons in real life:
1. Architecture and Design
- Urban Planning: Some cities, such as Canberra, Australia, and Chandigarh, India, incorporate hexagonal layouts in their street designs to facilitate traffic flow and optimize space.
- Building Facades: Hexagonal patterns are often used in architectural facades for their visual interest and structural benefits, as seen in modern buildings like the Honeycomb Apartments in Singapore.
- Tiling and Flooring: Hexagonal tiles are popular in interior design for their ability to create visually appealing and efficient floor patterns.
2. Natural Patterns
- Beehives: The hexagonal cells of a beehive are a classic example of how nature uses hexagons for efficient use of space and materials.
- Turtle Shells: Many turtle shells feature hexagonal patterns, contributing to their protective function while allowing flexibility.
- Basalt Columns: The Giant’s Causeway in Northern Ireland and Devil's Postpile in the USA are famous for their natural hexagonal basalt columns formed by volcanic activity.
3. Science and Technology
- Graphene: The structure of graphene, a single layer of carbon atoms arranged in a hexagonal lattice, has revolutionary applications in electronics due to its strength and conductivity.
- Metamaterials: Hexagonal arrangements are used in the design of metamaterials to create properties not found in nature, such as negative refractive index.
- Carbon Nanotubes: These cylindrical nanostructures, composed of hexagonal carbon atom lattices, have applications in materials science and nanotechnology.
4. Daily Objects
- Wrenches: Hexagonal nuts and bolts are common in tools and machinery, allowing for easy application of torque using wrenches.
- Packaging: Hexagonal packaging, such as honeycomb cardboard, is used for its strength and efficiency in cushioning and shipping goods.
- Paving: Hexagonal paving stones are used in landscaping for their durability and aesthetic appeal, as well as their interlocking capability.
5. Board Games and Art
- Board Games: Many board games, including "Settlers of Catan," utilize hexagonal tiles to create variable game boards that enhance strategic depth.
- Art: Hexagonal designs are popular in modern art and décor, used in creating patterns and structures that draw the eye and inspire creativity.
Hexagons, with their unique geometric properties, are integral to a wide range of applications, demonstrating their versatility and importance in various aspects of life.
Video hướng dẫn lớp 7 về cách tính chu vi của hình lục giác. Tìm hiểu các công thức và ví dụ minh họa về chu vi của hình lục giác trong bài giảng này.
Lớp 7: Chu Vi Hình Lục Giác
READ MORE:
Video về bài toán tính chu vi của hình lục giác đều, cung cấp hướng dẫn và giải thích chi tiết qua ví dụ thực tế. Thích hợp cho học sinh và người học muốn hiểu rõ hơn về chu vi của hình lục giác đều.
Chu Vi Hình Lục Giác Đều: Bài Toán Trong Ngày