Topic oval perimeter: The perimeter of an oval, or ellipse, is a fascinating geometric concept with practical applications in various fields. This guide will walk you through the different methods to approximate and calculate the oval perimeter, provide useful examples, and explore its significance in mathematics and real-world scenarios. Discover the formulas, properties, and tools you need to master the oval perimeter.
Table of Content
- Understanding the Perimeter of an Oval (Ellipse)
- Introduction
- Definition and Basic Concepts
- Mathematical Formulas
- Steps to Calculate Perimeter
- Examples and Applications
- Historical Context
- Fun Facts
- Frequently Asked Questions (FAQs)
- Additional Resources
- YOUTUBE: Xem video này để tìm hiểu về lý do tại sao không có công thức cụ thể cho chu vi của một hình ellipse và sự quan trọng của vấn đề này trong toán học.
Understanding the Perimeter of an Oval (Ellipse)
An oval, mathematically known as an ellipse, has a perimeter that is more complex to calculate compared to a circle. This guide provides formulas, examples, and interesting facts about the perimeter of an ellipse.
Formulas for Calculating the Perimeter
The perimeter \(P\) of an ellipse can be approximated using various formulas. Two commonly used approximations are:
- Ramanujan's Approximation:
- Approximation by Arithmetic-Geometric Mean:
\[P \approx \pi \left(a + b\right) \left(1 + \frac{3h}{10 + \sqrt{4 - 3h}}\right)\]
where \(a\) and \(b\) are the semi-major and semi-minor axes respectively, and \(h = \frac{(a - b)^2}{(a + b)^2}\).
\[P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}}\]
where \(a\) and \(b\) are the semi-major and semi-minor axes respectively.
Example Calculation
Consider an ellipse with a semi-major axis \(a = 10\) units and a semi-minor axis \(b = 5\) units.
Using the second approximation:
\[P \approx 2\pi \sqrt{\frac{10^2 + 5^2}{2}} = 2 \times 3.14 \times \sqrt{\frac{100 + 25}{2}} \approx 49.64\]
Interesting Facts about Ellipses
- Ellipses were first studied by the ancient Greek mathematician Menaechmus and were later named by Apollonius.
- Kepler discovered that the orbit of Mars is an ellipse with the Sun at one focus.
- A circle is a special case of an ellipse where the two foci coincide and the eccentricity is zero.
- Ellipses have various real-world applications, including planetary orbits and the design of certain mechanical parts like gears and cams.
Additional Information
The perimeter formulas provided are approximations because calculating the exact perimeter of an ellipse involves elliptic integrals, which are more complex. These approximations are generally sufficient for most practical purposes.
For more detailed calculations and applications, you can use online calculators or mathematical software.

READ MORE:
Introduction
Calculating the perimeter of an oval, also known as an ellipse, involves understanding its geometry and applying specific mathematical formulas. An ellipse is defined by its two axes: the major axis (the longest diameter) and the minor axis (the shortest diameter). Unlike a circle, the calculation of an ellipse's perimeter is not straightforward and requires approximation methods or complex integral calculations.
- An ellipse is created when a plane intersects a cone at an angle to its base.
- It has two focal points; the sum of distances from any point on the ellipse to these focal points is constant.
- The perimeter of an ellipse can be approximated using various formulas, such as Ramanujan's approximation or the exact integral formula involving elliptic integrals.
The most accurate method for calculating the perimeter involves elliptic integrals, but for practical purposes, simpler approximation formulas are often used. Understanding these methods can provide insights into the fascinating properties of ellipses and their applications in various fields, including engineering, astronomy, and design.
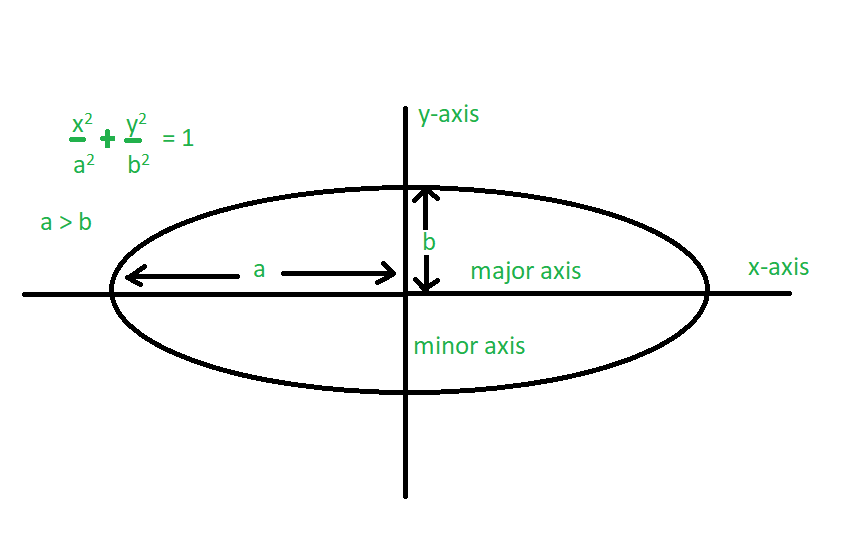
Definition and Basic Concepts
An oval, often referred to as an ellipse in geometry, is a closed curve resembling an elongated circle. The study of ellipses has deep historical roots, with notable contributions from mathematicians such as Euclid, Apollonius, and Kepler.
The basic components of an ellipse include:
- Major Axis: The longest diameter of the ellipse, spanning from one end to the other.
- Minor Axis: The shortest diameter, perpendicular to the major axis.
- Foci: Two fixed points inside the ellipse where the sum of the distances from any point on the ellipse to the foci is constant.
Ellipses have unique properties and applications:
- They are formed when a plane intersects a cone at an angle.
- A circle is a special case of an ellipse with equal major and minor axes.
- The eccentricity of an ellipse, which ranges between 0 and 1, measures its deviation from being circular.
To calculate the perimeter of an ellipse, several approximations can be used due to its complexity. One common formula is:
\[ P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \]
where \( a \) is the semi-major axis and \( b \) is the semi-minor axis.
Understanding these basic concepts is crucial for delving deeper into the geometric and algebraic properties of ellipses, which have numerous applications in fields such as astronomy, engineering, and physics.
Mathematical Formulas
The perimeter of an oval, commonly referred to as an ellipse in mathematical contexts, does not have a simple closed-form formula. However, several approximations can be used to calculate it. Here are some key formulas:
- Ramanujan's First Approximation:
- Ramanujan's Second Approximation:
- Series Expansion:
One of the most famous approximations is given by Ramanujan:
\[
P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]
\]
where \(a\) is the semi-major axis and \(b\) is the semi-minor axis.
Another approximation by Ramanujan provides greater accuracy:
\[
P \approx \pi \left[ a + b \right] \left[ 1 + \frac{3h}{10 + \sqrt{4 - 3h}} \right]
\]
where \(h = \left( \frac{a - b}{a + b} \right)^2\).
The perimeter can also be calculated using an infinite series:
\[
P = 2\pi a \left( 1 - \left(\frac{1}{2}\right)^2 e^2 - \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 e^4 - \left(\frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6}\right)^2 e^6 - \ldots \right)
\]
where \(e\) is the eccentricity of the ellipse, defined as \(e = \sqrt{1 - \frac{b^2}{a^2}}\).
These formulas help in estimating the perimeter of an ellipse, providing a deeper understanding of its geometric properties.
Steps to Calculate Perimeter
Calculating the perimeter of an oval, or ellipse, involves several steps due to its unique geometric properties. Here's a detailed guide:
- Identify the lengths of the major axis (\(2a\)) and the minor axis (\(2b\)) of the ellipse. The major axis is the longest diameter, while the minor axis is the shortest diameter.
- Calculate the semi-major axis (\(a\)) and the semi-minor axis (\(b\)) by dividing the lengths of the major and minor axes by 2, respectively.
- Use the approximate formula for the perimeter of an ellipse: \[ P \approx \pi \left( 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right) \] This is known as Ramanujan's first approximation.
- For a more accurate result, especially if the ellipse is not close to being a circle, use the following series expansion: \[ P \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \] This formula provides a reasonable approximation but is not exact.
- If greater precision is needed, use the complete elliptic integral of the second kind \(E(e)\), where \(e\) is the eccentricity of the ellipse: \[ P = 4aE(e) \] The eccentricity \(e\) is calculated as: \[ e = \sqrt{1 - \left(\frac{b}{a}\right)^2} \] And the complete elliptic integral \(E(e)\) can be computed using numerical methods or advanced calculators.
Following these steps will allow you to calculate the perimeter of an oval with a high degree of accuracy, suitable for various practical and mathematical applications.
Examples and Applications
The concept of the oval perimeter, especially when considering ellipses, finds numerous applications across various fields. Here are some examples and practical applications:
- Astronomy: The orbits of planets, satellites, and comets are often elliptical. Calculating the perimeter of these ellipses helps in understanding the distances these celestial bodies travel.
- Engineering: Elliptical shapes are used in designing components like gears, cams, and other mechanical parts. Knowing the perimeter aids in precise manufacturing and function.
- Architecture: Ellipses are used in the design of arches and domes. Calculating the perimeter ensures accuracy in construction and aesthetic appeal.
- Medical Imaging: Elliptical shapes are common in cross-sectional imaging techniques like MRI and CT scans. The perimeter helps in analyzing and interpreting the images correctly.
Here are a few step-by-step examples demonstrating the calculation of an ellipse's perimeter:
- Example 1: Find the perimeter of an ellipse with a semi-major axis of 10 units and a semi-minor axis of 5 units using Ramanujan's approximation formula.
- Solution: Use the formula \( P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \) where \( a \) is the semi-major axis and \( b \) is the semi-minor axis.
- Calculation:
- Given \( a = 10 \) and \( b = 5 \)
- Plugging in the values, \( P \approx 3.14 \left[ 3(10 + 5) - \sqrt{(3 \cdot 10 + 5)(10 + 3 \cdot 5)} \right] \)
- Simplify the expression to find the approximate perimeter.
- Example 2: Calculate the perimeter of an ellipse with \( a = 8 \) and \( b = 6 \) using the same approximation formula.
- Solution:
- Given \( a = 8 \) and \( b = 6 \)
- Using the formula, \( P \approx 3.14 \left[ 3(8 + 6) - \sqrt{(3 \cdot 8 + 6)(8 + 3 \cdot 6)} \right] \)
- Simplify to find the perimeter.
These examples highlight the practical applications and the methods used to approximate the perimeter of an ellipse, providing valuable insights into various real-world scenarios.
Historical Context
The mathematical study of ellipses dates back to ancient Greece, where significant contributions were made by prominent mathematicians. Menaechmus, a student of Plato, is credited with the discovery of the ellipse through his work on conic sections. This discovery laid the groundwork for further explorations in geometry and mathematics.
Euclid, another Greek mathematician, provided systematic studies of conic sections, including ellipses, in his work "Elements." However, it was Apollonius of Perga who significantly advanced the understanding of ellipses in his famous treatise "Conics," where he named the curve "ellipse" and systematically described its properties.
During the Hellenistic period, Pappus of Alexandria made notable contributions by examining the focus and directrix of an ellipse, which are essential for understanding its geometric properties.
The ellipse also played a crucial role in the astronomical theories of Johannes Kepler in the 17th century. Kepler discovered that the planets orbit the Sun in elliptical paths, not circular ones, with the Sun at one of the foci. This was a monumental shift in the understanding of our solar system and provided empirical support for the heliocentric model proposed by Copernicus.
In the 19th and 20th centuries, the study of ellipses continued to evolve with the works of mathematicians like Carl Friedrich Gauss and Srinivasa Ramanujan. Ramanujan, in particular, developed several approximation formulas for calculating the perimeter of an ellipse, which are still used today due to their remarkable accuracy.
- Menaechmus: Discovery of the ellipse through conic sections.
- Euclid: Systematic study of conic sections in "Elements."
- Apollonius of Perga: Advanced the understanding and terminology of ellipses in "Conics."
- Pappus of Alexandria: Explored the focus and directrix of an ellipse.
- Johannes Kepler: Discovered the elliptical orbits of planets, revolutionizing astronomy.
- Carl Friedrich Gauss: Contributed to the mathematical theory of ellipses.
- Srinivasa Ramanujan: Developed approximation formulas for the perimeter of an ellipse.
The historical development of the ellipse and its perimeter formula illustrates the collaborative nature of mathematical discovery, spanning cultures and centuries. From ancient Greece to modern times, the ellipse has remained a subject of fascination and utility in various fields, including astronomy, engineering, and architecture.
Fun Facts
Ellipses and ovals are fascinating shapes with many interesting properties and applications. Here are some fun facts about them:
- An ellipse was first studied by Menaechmus and further investigated by Euclid. Apollonius named it, and Kepler discovered that planetary orbits, such as Mars, are elliptical.
- Both circles and ellipses are conic sections. A circle is a special case of an ellipse where the major and minor axes are equal.
- The sum of the distances from any point on an ellipse to its two foci is constant, which is a unique property not shared by circles.
- Ellipses are formed when a plane intersects a cone at an angle to its base, which is neither perpendicular nor parallel.
- The eccentricity of an ellipse is a measure of how "stretched" it is. It ranges from 0 (a circle) to values approaching 1 (a highly elongated shape).
- Ellipses have practical applications in astronomy (planetary orbits), engineering (design of reflective surfaces), and architecture (whispering galleries).
- Real-world examples of ellipses include the orbits of planets, satellites, and comets, as well as the shapes of some boat keels, rudders, and airplane wings.
- Running tracks are often elliptical. Most modern outdoor tracks are 400 meters in circumference, but historically, tracks varied in length, including 440 yards and even 500 meters in some cases.
- The elliptical shape is used in design and construction due to its aesthetic appeal and structural properties. For example, the St. Peter's Square in Vatican City has an elliptical layout.
Frequently Asked Questions (FAQs)
-
What is the perimeter of a circle?
The perimeter (or circumference) of a circle can be calculated using the formula \(C = 2\pi r\), where \(r\) is the radius of the circle. For example, if the radius of the circle is 5 units, the circumference would be \(C = 2\pi \times 5 = 10\pi \approx 31.42\) units.
-
How do you find the perimeter of an ellipse?
The perimeter of an ellipse (commonly called an oval) does not have a simple exact formula like a circle. However, one of the best known approximations is given by Ramanujan's formula:
\[
P \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right]
\]
where \(a\) is the semi-major axis and \(b\) is the semi-minor axis of the ellipse. For a more precise calculation, you might use an infinite series or numerical methods. -
What are the practical uses of calculating the perimeter of an ellipse?
Calculating the perimeter of an ellipse is useful in various fields such as:
- Astronomy: Understanding the orbits of planets and satellites which are often elliptical in shape.
- Engineering: Designing components like gears, cams, and optical lenses that have elliptical shapes.
- Architecture: Creating aesthetic and structurally sound designs, such as elliptical arches and domes.

Additional Resources
- : This website provides an easy-to-understand explanation of ovals and their properties, including the perimeter calculation.
- : Math Open Reference offers a detailed guide on calculating the perimeter of an oval, along with interactive demonstrations.
- : WikiHow provides a step-by-step tutorial with illustrations on how to find the perimeter of an oval.
Xem video này để tìm hiểu về lý do tại sao không có công thức cụ thể cho chu vi của một hình ellipse và sự quan trọng của vấn đề này trong toán học.
Tại sao không có công thức tính chu vi của một hình ellipse‽
Xem video này để biết cách tính diện tích và chu vi của hình oval (hình ellipse) trên mặt đất, cùng với các phương pháp tính toán và ứng dụng thực tế.
Cách tính diện tích và chu vi của hình oval (hình ellipse) trên mặt đất?