Topic what is one squared: Understanding the concept of squaring a number is fundamental in mathematics. When we square the number one, we simply multiply it by itself, resulting in one. This concept, though simple, forms the basis for more complex mathematical principles and operations. Read on to explore the significance and applications of squaring numbers in various mathematical contexts.
Table of Content
- Understanding One Squared
- Introduction to Squaring
- Understanding One Squared
- Mathematical Representation
- Perfect Squares and Their Properties
- Applications of Squaring in Geometry
- Square Roots and Their Relation to Squaring
- Common Misconceptions About Squaring
- Practical Examples of Squaring
- Calculating Squares Using Different Methods
- Conclusion
- YOUTUBE: Negative One Squared?... Comparing -1² vs. (-1)²
Understanding One Squared
In mathematics, squaring a number means multiplying the number by itself. The notation for squaring a number \( n \) is \( n^2 \), which is pronounced as "n squared." Here, we will explore what it means to square the number one.
Definition and Calculation
When we square the number one, we perform the following calculation:
\[ 1^2 = 1 \times 1 = 1 \]
Thus, one squared is equal to one. This operation is a simple example of exponentiation, where the base (1) is raised to the power of 2.
Properties of Squaring One
- Perfect Square: The number one is a perfect square because it is the product of an integer (1) multiplied by itself.
- Area Representation: In geometry, a square with sides of length one unit has an area of one square unit. This visual representation helps in understanding the concept of squaring.
- Identity Property: Squaring one does not change its value, which illustrates the identity property of multiplication.
Table of Perfect Squares
| Number | Square |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Application in Algebra
The square of a number, including one, is frequently used in algebraic equations and formulas. For example, solving quadratic equations often involves squaring numbers.
Visualizing Squaring
When visualizing squaring, consider a square shape. A square with a side length of 1 unit will cover an area of:
\[ \text{Area} = 1 \text{ unit} \times 1 \text{ unit} = 1 \text{ square unit} \]
Summary
Squaring the number one is a fundamental mathematical operation that results in one. It serves as a basic example to understand the concept of squaring and is essential in various mathematical applications.
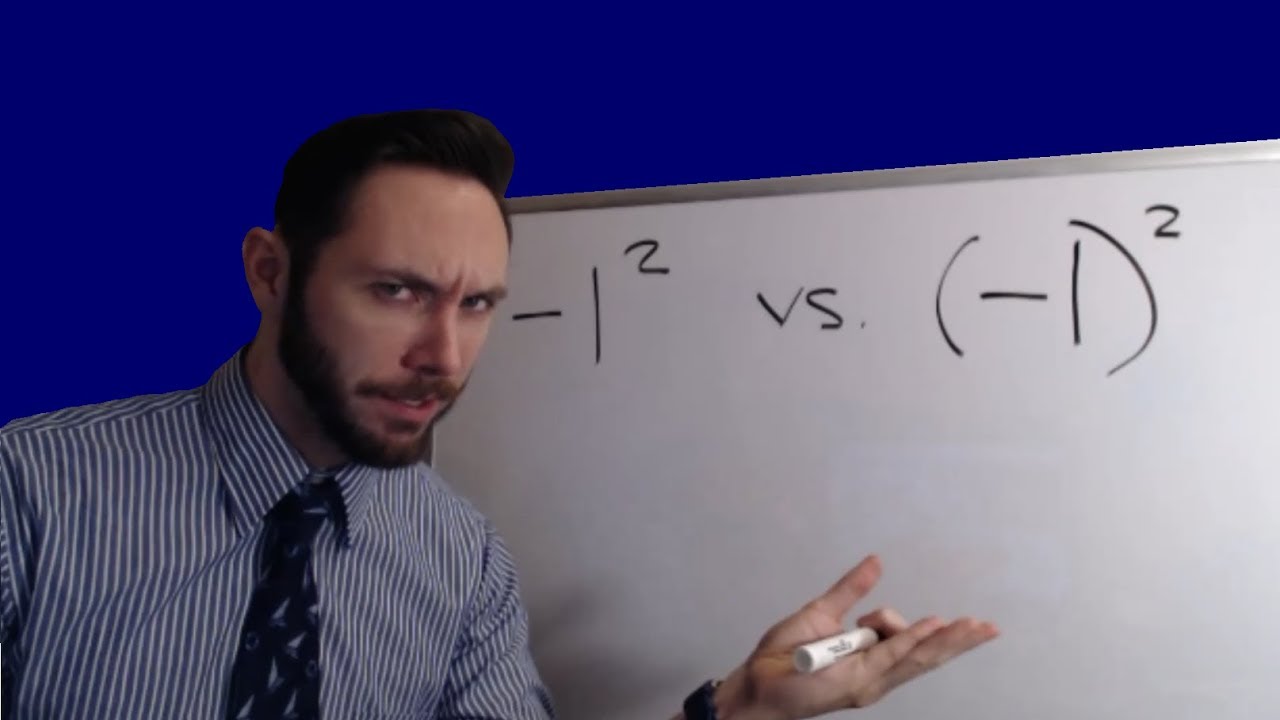
READ MORE:
Introduction to Squaring
Squaring a number means multiplying the number by itself. This operation is denoted with an exponent of 2. For example, 1 squared is written as \( 1^2 \), which is equal to \( 1 \times 1 = 1 \). Squaring is a fundamental mathematical operation used in various fields, including algebra, geometry, and physics. It helps in understanding areas of squares and solving quadratic equations.
Here are some key points about squaring:
- Squaring a number always results in a positive value because a positive times a positive is positive, and a negative times a negative is also positive.
- Perfect squares are numbers that are the squares of integers. For instance, \( 1^2 = 1 \), \( 2^2 = 4 \), and \( 3^2 = 9 \).
- The square root of a squared number returns the original number. For example, \( \sqrt{1^2} = 1 \).
- Squaring is represented in various notations such as \( x \times x \), \( x^2 \), or using the exponentiation symbol in programming and calculators.
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Understanding squaring is crucial for learning higher-level math concepts and solving practical problems involving areas and volumes.
Understanding One Squared
Squaring a number means multiplying the number by itself. In the case of one squared, the calculation is straightforward:
- Start with the number: 1
- Multiply it by itself: 1 × 1
- The result is: 1
Therefore, 1 squared is 1, which can be written mathematically as \(1^2 = 1\).
This concept is fundamental in mathematics and helps in understanding larger concepts such as perfect squares, algebra, and geometry. Squaring is used in various fields, from calculating areas to solving quadratic equations.
Mathematical Representation
When we talk about squaring a number, we refer to multiplying the number by itself. In mathematical terms, squaring a number \( n \) is expressed as \( n^2 \). This operation is fundamental in various branches of mathematics and its applications.
Let's look at the mathematical representation of squaring with the example of the number 1:
- The base number: \( 1 \)
- The exponent: \( 2 \)
To square the number 1, we perform the following calculation:
\[
1^2 = 1 \times 1 = 1
\]
This indicates that one squared is equal to one.
Here are the steps to understand the squaring process:
- Identify the number to be squared (in this case, 1).
- Multiply this number by itself: \( 1 \times 1 \).
- Write the result: \( 1^2 = 1 \).
In addition, squaring can also be visualized geometrically. A square with side length 1 unit has an area of 1 square unit, which is another way to understand that \( 1^2 = 1 \).
Mathematically, the properties of squaring can be extended to include various identities and properties such as:
- Perfect squares: numbers that are squares of integers (e.g., 1, 4, 9, 16, etc.).
- Squares of negative numbers: always positive, since \( (-n)^2 = n^2 \).
- Use in algebra: solving equations involving squared terms.
Understanding the concept of squaring is essential for progressing in mathematics, especially in algebra and geometry where these principles are frequently applied.
Perfect Squares and Their Properties
Perfect squares are numbers that are the product of an integer multiplied by itself. These numbers have unique properties and applications in various fields of mathematics. Understanding perfect squares is essential for solving quadratic equations, simplifying square roots, and grasping geometric concepts.
Definition and Examples
A perfect square is defined as \( n^2 \), where \( n \) is an integer. For example:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
Properties of Perfect Squares
- Always Non-negative: The square of any real number is non-negative. Thus, perfect squares are always positive or zero.
- Ends in Specific Digits: In base 10, a perfect square can end only in 0, 1, 4, 5, 6, or 9.
- Sum of Odd Numbers: A perfect square is the sum of the first n odd numbers. For example, \( 1 + 3 = 4 = 2^2 \).
Applications of Perfect Squares
Perfect squares are used in various mathematical computations and theories, including:
- Geometry: Calculating areas of squares and other geometric figures.
- Algebra: Simplifying expressions and solving equations involving quadratic terms.
- Number Theory: Understanding properties of integers and their factorizations.
Visualizing Perfect Squares
Perfect squares can be visualized geometrically. For instance, a square with side length 3 has an area of \( 3 \times 3 = 9 \). This helps in comprehending why the term "square" is used.
| Integer | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |

Applications of Squaring in Geometry
Squaring is a fundamental mathematical operation with significant applications in geometry. Understanding how squaring is used can provide insights into various geometric concepts and calculations.
- Area Calculation:
One of the most common applications of squaring in geometry is in calculating the area of squares. The area (A) of a square with side length (s) is given by the formula:
\[ A = s^2 \]
- Pythagorean Theorem:
The Pythagorean theorem uses squaring to relate the lengths of the sides of a right triangle. For a right triangle with legs (a) and (b) and hypotenuse (c), the relationship is:
\[ a^2 + b^2 = c^2 \]
- Distance Formula:
In coordinate geometry, the distance between two points (x1, y1) and (x2, y2) in the plane can be calculated using squaring:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Circle Area and Radius:
The area (A) of a circle with radius (r) is another example where squaring is essential:
\[ A = \pi r^2 \]
- Volume of a Cube:
The volume (V) of a cube with side length (s) involves squaring as part of the calculation:
\[ V = s^3 \]
- Standard Deviation:
In statistics, the squaring of deviations from the mean is used to calculate variance and standard deviation, important measures in geometric contexts.
\[ \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \]
These examples illustrate how squaring is a powerful tool in geometry, providing a basis for calculating areas, distances, and other important geometric properties.
Square Roots and Their Relation to Squaring
The concept of square roots is deeply interconnected with the idea of squaring numbers. When a number is squared, it is multiplied by itself. The square root of a number is the value that, when squared, gives the original number. For example, since \(1 \times 1 = 1\), the square root of 1 is 1.
Understanding square roots involves a few key concepts:
- Non-negative Real Numbers: Every non-negative real number has a non-negative square root.
- Perfect Squares: Numbers like 1, 4, 9, and 16, which are squares of integers, have integer square roots.
- Imaginary Numbers: The square root of negative numbers involves imaginary units. For instance, the square root of -1 is denoted as \(i\).
Here's a detailed look at the relationship between squaring and square roots:
| Number | Square | Square Root |
| 1 | 1 | 1 |
| 4 | 16 | 2 |
| 9 | 81 | 3 |
To find the square root of a number, you can use various methods such as prime factorization, estimation, or a calculator. The concept of square roots is essential in many mathematical contexts, including solving quadratic equations and understanding geometric properties like distances and areas.
Common Misconceptions About Squaring
Understanding the concept of squaring can sometimes lead to various misconceptions. Below are some of the most common misunderstandings and clarifications to help dispel these myths:
- Misconception 1: Squaring a number always makes it larger.
While squaring a positive number indeed makes it larger (e.g., \(2^2 = 4\)), squaring a fraction between 0 and 1 actually makes it smaller (e.g., \(\left(\frac{1}{2}\right)^2 = \frac{1}{4}\)).
- Misconception 2: The square of a negative number is negative.
This is incorrect. When you square a negative number, the result is positive because a negative times a negative is a positive (e.g., \((-3)^2 = 9\)).
- Misconception 3: Squaring and multiplying by 2 are the same.
Squaring a number means multiplying it by itself (e.g., \(3^2 = 3 \times 3 = 9\)), whereas multiplying by 2 simply doubles the number (e.g., \(3 \times 2 = 6\)). These operations yield different results.
- Misconception 4: The square root is always a whole number.
Not all squares have whole number roots. For example, the square root of 2 is approximately 1.414, which is an irrational number.
- Misconception 5: Squaring and taking the square root are always inverse operations.
While this is true for non-negative numbers (e.g., \(\sqrt{4} = 2\)), it doesn't hold for negative numbers since the square root of a negative number is not a real number.
- Misconception 6: Perfect squares are always positive.
In the context of real numbers, this is true. However, in the complex number system, numbers can have negative squares (e.g., \(i^2 = -1\), where \(i\) is the imaginary unit).
By understanding these misconceptions, learners can develop a stronger and more accurate grasp of mathematical principles related to squaring.
Practical Examples of Squaring
Squaring is a fundamental mathematical operation with numerous practical applications. Here are some detailed examples to illustrate the concept:
1. Area Calculation
One of the most common applications of squaring is in calculating the area of a square. The area \(A\) of a square is given by the formula:
\[ A = s^2 \]
where \(s\) is the length of one side of the square. For example, if each side of a square is 5 units long, the area is:
\[ A = 5^2 = 25 \text{ square units} \]
2. Pythagorean Theorem
The Pythagorean theorem is a significant application of squaring in geometry. It states that in a right-angled triangle, the square of the hypotenuse \(c\) is equal to the sum of the squares of the other two sides \(a\) and \(b\):
\[ c^2 = a^2 + b^2 \]
For instance, if \(a = 3\) units and \(b = 4\) units, the hypotenuse \(c\) can be found as:
\[ c^2 = 3^2 + 4^2 = 9 + 16 = 25 \]
Thus, \(c = \sqrt{25} = 5\) units.
3. Profit Maximization in Business
Quadratic functions, which involve squaring, are used to maximize profits in business. For example, if a lemonade stand’s profit \(P\) is modeled by the quadratic equation:
\[ P = -p^2 + 12p - 20 \]
where \(p\) is the price per glass. By completing the square or using calculus, one can determine the optimal price to maximize profit.
4. Physics and Projectile Motion
In physics, squaring is essential in the equations of motion. For instance, the height \(h\) of a projectile thrown into the air is given by:
\[ h = v_0 t - \frac{1}{2} g t^2 \]
where \(v_0\) is the initial velocity, \(g\) is the acceleration due to gravity, and \(t\) is the time. Squaring the time component helps in determining the projectile's path.
5. Electrical Engineering
In electrical engineering, the power \(P\) dissipated in a resistor is calculated using the square of the voltage \(V\) across the resistor divided by the resistance \(R\):
\[ P = \frac{V^2}{R} \]
This formula illustrates how squaring the voltage affects the power dissipation in circuits.
6. Algebra and Quadratic Equations
Solving quadratic equations is a direct application of squaring. A standard quadratic equation is of the form:
\[ ax^2 + bx + c = 0 \]
The solutions to this equation, known as the roots, are found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
This demonstrates the critical role of squaring in finding the solutions to quadratic equations.

Calculating Squares Using Different Methods
Squaring a number involves multiplying the number by itself. Here are several methods to calculate squares:
1. Traditional Multiplication
This is the most straightforward method, where you simply multiply the number by itself:
\[ x^2 = x \times x \]
For example, to calculate \( 5^2 \):
\[ 5^2 = 5 \times 5 = 25 \]
2. Base Method
This method is useful for squaring numbers near a base (e.g., 10, 100). The steps are:
- Identify the base (e.g., 10, 100) close to the number.
- Calculate the difference between the number and the base.
- Square the difference.
- Adjust the result based on the base.
For example, to calculate \( 104^2 \) using base 100:
- Base = 100
- Difference = \( 104 - 100 = 4 \)
- Square the difference: \( 4^2 = 16 \)
- Calculate: \( 100 \times (104 + 4) = 108 \times 100 = 10800 \)
- Combine the results: \( 10800 + 16 = 10816 \)
3. Duplex Method
This method involves breaking the number into smaller parts and applying a specific formula:
- Split the number into two parts.
- Square each part and sum the results.
- Add double the product of the parts.
For example, to calculate \( 53^2 \):
- Split into 50 and 3
- Calculate: \( 50^2 = 2500 \)
- Calculate: \( 3^2 = 9 \)
- Double the product: \( 2 \times 50 \times 3 = 300 \)
- Sum the results: \( 2500 + 9 + 300 = 2809 \)
4. Squaring Numbers Ending in 5
For numbers ending in 5, a special trick can be used:
- Identify the number without the 5.
- Multiply this number by itself plus one.
- Append 25 to the result.
For example, to calculate \( 35^2 \):
- Number without 5 = 3
- Calculate: \( 3 \times 4 = 12 \)
- Append 25: \( 1225 \)
5. Using Algebraic Identities
Using algebraic identities can simplify squaring:
- \( (a + b)^2 = a^2 + b^2 + 2ab \)
- \( (a - b)^2 = a^2 + b^2 - 2ab \)
For example, to calculate \( 47^2 \) using \( (a + b)^2 \):
- Identify a = 50, b = 3
- Apply the formula: \( 50^2 + 3^2 + 2 \times 50 \times (-3) = 2500 + 9 - 300 = 2209 \)
6. Using Calculators and Software
Modern calculators and software can quickly compute squares using built-in functions. Simply enter the number and use the square function.
Conclusion
Understanding and using different methods to calculate squares can enhance your mathematical skills and speed. Practice these methods to find the one that suits you best.
Conclusion
Understanding the concept of squaring is fundamental in mathematics. The operation of squaring a number, represented as \( n^2 \), involves multiplying the number by itself. This process has broad applications across various mathematical disciplines and real-world scenarios, including geometry, algebra, and everyday problem-solving.
Through our exploration, we have seen that squaring numbers leads to the creation of perfect squares, which have unique properties and applications. For instance, perfect squares are always non-negative, and the square of any integer results in a perfect square. Additionally, the square root of a perfect square returns the original number.
We have also addressed common misconceptions about squaring, such as the difference between squaring positive and negative numbers. It's crucial to remember that squaring a negative number results in a positive product, while squaring a positive number also yields a positive product.
Calculating squares can be done using various methods, including direct multiplication, using algebraic identities, or employing technological tools like calculators. Each method offers a different perspective and utility depending on the context and complexity of the numbers involved.
In conclusion, the operation of squaring numbers is a simple yet powerful mathematical tool. By understanding its principles and applications, one can enhance their mathematical proficiency and apply this knowledge to various fields, from academic studies to practical everyday situations.
Negative One Squared?... Comparing -1² vs. (-1)²
i squared All 4 One
Expand & Simplify brackets, one squared
What Is Seconds Squared? (Acceleration Unit Explained)
Squared Squares - Numberphile
–1 squared minus (– 1) squared =? A BASIC Math problem MANY will get WRONG!
READ MORE: