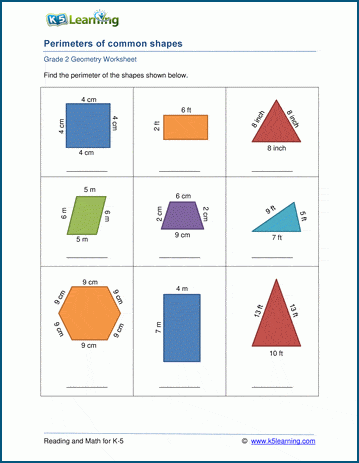
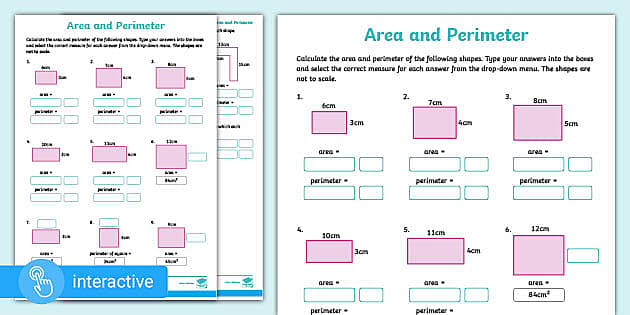
Topic the perimeter of an equilateral triangle: The perimeter of an equilateral triangle is a fundamental concept in geometry, involving simple yet essential calculations. Understanding how to determine the perimeter is crucial for students and enthusiasts of mathematics. In this article, we explore the definition, properties, and practical applications of equilateral triangles, ensuring a comprehensive grasp of the topic.
Table of Content
- Equilateral Triangle
- Introduction to Equilateral Triangles
- Definition and Properties
- Formulas and Calculations
- Perimeter of an Equilateral Triangle
- Area of an Equilateral Triangle
- Height of an Equilateral Triangle
- Special Characteristics
- Comparison with Other Triangles
- Equilateral Triangle Theorems
- Applications in Real Life
- Practice Problems and Solutions
- Frequently Asked Questions
- YOUTUBE: Hướng dẫn cách tính chu vi của tam giác đều một cách dễ hiểu và nhanh chóng. Phù hợp cho học sinh và người mới bắt đầu.
Equilateral Triangle
Definition
An equilateral triangle is a triangle in which all three sides are equal in length and all three internal angles are congruent, each measuring 60 degrees.
Properties
- All sides are equal: \(AB = BC = CA\)
- All internal angles are equal: \(\angle ABC = \angle BCA = \angle CAB = 60^\circ\)
- Has three lines of symmetry
- Altitude, median, angle bisector, and perpendicular bisector all coincide
- Centroid, orthocenter, circumcenter, and incenter are the same point
Formulas
Perimeter
The perimeter of an equilateral triangle is calculated by adding all three sides. Since all sides are equal, the formula is:
\[
\text{Perimeter} = 3a
\]
where \(a\) is the length of one side.
Area
The area of an equilateral triangle can be found using the formula:
\[
\text{Area} = \frac{\sqrt{3}}{4}a^2
\]
where \(a\) is the length of one side.
Height
The height (altitude) of an equilateral triangle is given by:
\[
h = \frac{\sqrt{3}}{2}a
\]
Radius of Circumcircle
The radius of the circumscribed circle (circumradius) is:
\[
R = \frac{a\sqrt{3}}{3}
\]
Radius of Incircle
The radius of the inscribed circle (inradius) is:
\[
r = \frac{a\sqrt{3}}{6}
\]
Example Calculation
For an equilateral triangle with a side length of 6 cm:
- Perimeter: \( P = 3 \times 6 = 18 \) cm
- Area: \(\text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = 9\sqrt{3} \approx 15.59 \) cm2
- Height: \( h = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \approx 5.20 \) cm
- Circumradius: \( R = \frac{6\sqrt{3}}{3} = 2\sqrt{3} \approx 3.46 \) cm
- Inradius: \( r = \frac{6\sqrt{3}}{6} = \sqrt{3} \approx 1.73 \) cm
Conclusion
The equilateral triangle is a fundamental geometric shape with unique properties and simple formulas for calculating its dimensions, making it an essential topic in geometry.

READ MORE:
Introduction to Equilateral Triangles
An equilateral triangle is a type of polygon where all three sides are of equal length, and all three interior angles are equal to 60 degrees. This symmetry gives the equilateral triangle several unique properties that make it a fundamental shape in geometry.
The term "equilateral" comes from the Latin words "equi," meaning equal, and "lateral," meaning side. Thus, an equilateral triangle is defined by its equal sides and angles. This type of triangle is not only aesthetically pleasing but also appears frequently in various fields such as architecture, art, and nature.
In an equilateral triangle, several geometric concepts coincide, including the centroid, orthocenter, and circumcenter, which are all the same point due to the triangle's perfect symmetry. The altitude, median, and angle bisector in an equilateral triangle are also the same line segments, each dividing the triangle into two 30-60-90 right triangles.
Here are some key properties and formulas related to equilateral triangles:
- Perimeter: The perimeter \( P \) of an equilateral triangle with side length \( a \) is given by \( P = 3a \).
- Area: The area \( A \) can be calculated using the formula \( A = \frac{\sqrt{3}}{4}a^2 \).
- Height: The height \( h \) (or altitude) of an equilateral triangle can be found using \( h = \frac{\sqrt{3}}{2}a \).
These properties make the equilateral triangle an interesting and important shape in mathematics. Whether used in the construction of buildings or in solving complex mathematical problems, the equilateral triangle's consistent properties and ratios are highly valuable.
Definition and Properties
An equilateral triangle is a triangle in which all three sides are of equal length and all three interior angles are equal to 60 degrees. This unique property makes the equilateral triangle a regular polygon.
Below are some key properties and formulas associated with equilateral triangles:
- Equal Sides: All sides are congruent, meaning each side has the same length denoted as \(a\).
- Equal Angles: Each interior angle is 60 degrees.
- Perimeter: The perimeter \(P\) of an equilateral triangle can be calculated as \(P = 3a\).
- Semi-Perimeter: The semi-perimeter \(s\) is half of the perimeter, given by \(s = \frac{3a}{2}\).
- Area: The area \(A\) of an equilateral triangle can be calculated using the formula \(A = \frac{\sqrt{3}}{4}a^2\).
- Altitude: The altitude \(h\) (height) can be found using \(h = \frac{\sqrt{3}}{2}a\).
These properties make equilateral triangles a fundamental shape in geometry, often used in various mathematical calculations and real-world applications such as construction and design.
Formulas and Calculations
Calculating the perimeter of an equilateral triangle involves a simple formula. An equilateral triangle is a triangle in which all three sides are equal in length. Given this property, the perimeter can be calculated using the following formula:
Perimeter Formula:
\[ P = 3a \]
where \( P \) is the perimeter and \( a \) is the length of one side of the equilateral triangle.
Step-by-Step Calculation
- Identify the length of one side (a): Measure or note the length of one side of the equilateral triangle.
- Multiply by 3: Multiply the length of the side by 3 to get the perimeter.
For example, if the length of one side is 5 units, the calculation would be:
\[ P = 3 \times 5 = 15 \text{ units} \]
Example Calculation
Consider an equilateral triangle with each side of length 7 units. To find the perimeter:
- Length of one side (a): 7 units
- Apply the formula:
- \[ P = 3 \times 7 = 21 \text{ units} \]
Table of Perimeter Calculations
| Side Length (a) | Perimeter (P) |
|---|---|
| 2 units | \[ P = 3 \times 2 = 6 \text{ units} \] |
| 4 units | \[ P = 3 \times 4 = 12 \text{ units} \] |
| 6 units | \[ P = 3 \times 6 = 18 \text{ units} \] |
| 10 units | \[ P = 3 \times 10 = 30 \text{ units} \] |
Using this formula, you can easily calculate the perimeter of any equilateral triangle as long as you know the length of one side.
Perimeter of an Equilateral Triangle
The perimeter of an equilateral triangle is the total length around the triangle. Since all sides of an equilateral triangle are of equal length, calculating the perimeter is straightforward.
To find the perimeter of an equilateral triangle, you can use the following formula:
\[ P = 3a \]
Where:
- P is the perimeter
- a is the length of one side of the triangle
This formula simply multiplies the length of one side by three because all three sides are equal. For example, if each side of the triangle is 5 units long, the perimeter would be:
\[ P = 3 \times 5 = 15 \, \text{units} \]
Step-by-Step Calculation
- Measure the length of one side of the equilateral triangle. Let's call this length a.
- Multiply the length of the side by 3 using the formula: P = 3a.
- The result is the perimeter of the equilateral triangle.
Here is a practical example to illustrate this:
- If the side length of an equilateral triangle is 10 units, then the perimeter is:
- \[ P = 3 \times 10 = 30 \, \text{units} \]
Thus, the perimeter is 30 units.
Using this method, you can easily determine the perimeter of any equilateral triangle as long as you know the length of one side.

Area of an Equilateral Triangle
The area of an equilateral triangle can be calculated using a specific formula derived from its geometric properties. Here, we will explore the formula and the steps involved in calculating the area.
Formula for the Area
The formula for finding the area of an equilateral triangle is:
\[
\text{Area} = \frac{\sqrt{3}}{4} a^2
\]
where \( a \) is the length of a side of the equilateral triangle.
Derivation of the Formula
- Draw an equilateral triangle and an altitude from one vertex to the opposite side, dividing the triangle into two congruent right triangles.
- Using the Pythagorean theorem in one of the right triangles, calculate the height \( h \):
\[
h = \frac{\sqrt{3}}{2} a
\] - Substitute the height into the standard formula for the area of a triangle \( A = \frac{1}{2} \times \text{base} \times \text{height} \):
\[
A = \frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2
\]
Step-by-Step Calculation
Let's go through an example calculation to illustrate the process.
Example: Find the area of an equilateral triangle with a side length of 6 cm.
- Identify the side length: \( a = 6 \) cm.
- Plug the side length into the formula:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \, \text{cm}^2
\] - Simplify the expression to get the final area:
\[
\text{Area} \approx 15.59 \, \text{cm}^2
\]
Properties of an Equilateral Triangle
- All sides are equal in length.
- All internal angles are equal, each measuring \( 60^\circ \).
- It is a regular polygon with three equal sides and three equal angles.
- The altitude, median, angle bisector, and perpendicular bisector coincide.
Examples of Using the Area Formula
- Example 1: For an equilateral triangle with a side length of 8 cm, the area is:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 8^2 = 16\sqrt{3} \approx 27.71 \, \text{cm}^2
\] - Example 2: For a triangle with a side length of 5 cm, the area is:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 5^2 = \frac{\sqrt{3}}{4} \times 25 = 6.25\sqrt{3} \approx 10.83 \, \text{cm}^2
\]
Height of an Equilateral Triangle
The height of an equilateral triangle is the perpendicular line segment drawn from a vertex to the midpoint of the opposite side. This height divides the triangle into two 30-60-90 right triangles.
Formula to Calculate the Height
The height (\(h\)) of an equilateral triangle with side length (\(a\)) can be calculated using the following formula:
\[
h = \frac{\sqrt{3}}{2} a
\]
Step-by-Step Calculation
- Identify the side length (\(a\)) of the equilateral triangle.
- Substitute the side length into the height formula.
- Simplify to find the height.
Example Calculation
Let's calculate the height of an equilateral triangle with a side length of 6 units:
\[
h = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \approx 5.2 \text{ units}
\]
Height from Perimeter
If the perimeter (\(P\)) of an equilateral triangle is given, the side length can be found as:
\[
a = \frac{P}{3}
\]
Then, use the side length to find the height:
\[
h = \frac{\sqrt{3}}{2} \times \frac{P}{3} = \frac{P\sqrt{3}}{6}
\]
Height from Area
If the area (\(A\)) of an equilateral triangle is known, use the area to find the side length first:
\[
A = \frac{\sqrt{3}}{4} a^2 \implies a = \sqrt{\frac{4A}{\sqrt{3}}}
\]
Then, substitute the side length into the height formula:
\[
h = \frac{\sqrt{3}}{2} \sqrt{\frac{4A}{\sqrt{3}}}
\]
Examples
- Given side length 4 units:
\[
h = \frac{\sqrt{3}}{2} \times 4 = 2\sqrt{3} \approx 3.46 \text{ units}
\] - Given perimeter 18 units:
\[
a = \frac{18}{3} = 6 \text{ units}
\]\[
h = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \approx 5.2 \text{ units}
\] - Given area 16 square units:
\[
a = \sqrt{\frac{4 \times 16}{\sqrt{3}}} = \sqrt{\frac{64}{\sqrt{3}}} \approx 5.4 \text{ units}
\]\[
h = \frac{\sqrt{3}}{2} \times 5.4 \approx 4.68 \text{ units}
\]
Special Characteristics
An equilateral triangle, being a regular polygon, has unique properties and characteristics that distinguish it from other triangles. Here are some of the notable features:
- Equal Sides and Angles: All three sides of an equilateral triangle are of equal length, and each internal angle measures 60 degrees. This symmetry contributes to its regular polygon status.
- Symmetry: An equilateral triangle has three lines of symmetry. Each line of symmetry passes through a vertex and the midpoint of the opposite side.
- Concurrent Lines: The altitude, median, angle bisector, and perpendicular bisector from each vertex coincide, forming a single line for each side. These three lines intersect at a single point known as the centroid, which is also the orthocenter, circumcenter, and incenter of the triangle.
- Altitude: The altitude of an equilateral triangle can be calculated using the formula:
\[ \text{Height} = \frac{s\sqrt{3}}{2} \] where \(s\) is the length of a side. - Area: The area is given by the formula:
\[ \text{Area} = \frac{s^2\sqrt{3}}{4} \] This demonstrates the relationship between the side length and the area of the triangle. - Circles:
- Circumcircle: The radius of the circumcircle (circumradius) is:
\[ R = \frac{s\sqrt{3}}{3} \] - Incircle: The radius of the incircle (inradius) is:
\[ r = \frac{s\sqrt{3}}{6} \]
- Circumcircle: The radius of the circumcircle (circumradius) is:
- Relations: The circumradius is exactly twice the inradius (\(R = 2r\)).
- Point Properties: For any point inside the equilateral triangle, the sum of the distances from this point to the three sides is equal to the length of the altitude.
These characteristics make the equilateral triangle a fascinating subject in geometry, with numerous applications in various fields of science and mathematics.
Comparison with Other Triangles
Triangles come in various forms, each with unique characteristics. Let's explore how an equilateral triangle compares with other types of triangles.
- Equilateral Triangle:
- All three sides are equal.
- All three angles are equal, each measuring \(60^\circ\).
- It is a special case of an isosceles triangle where not just two but all three sides are equal.
- Isosceles Triangle:
- Has at least two equal sides.
- Two angles opposite the equal sides are also equal.
- While every equilateral triangle is isosceles, not all isosceles triangles are equilateral.
- Scalene Triangle:
- No sides are equal.
- No angles are equal.
- Scalene triangles have the most general form without any specific symmetry properties.
- Right Triangle:
- Has one angle equal to \(90^\circ\).
- The sides opposite the right angle (the hypotenuse) is the longest side.
- Can be scalene (if all sides are different) or isosceles (if the other two sides are equal).
- Acute Triangle:
- All three angles are less than \(90^\circ\).
- Can be equilateral if all angles are \(60^\circ\).
- Can also be isosceles or scalene.
- Obtuse Triangle:
- Has one angle greater than \(90^\circ\).
- Cannot be equilateral.
- Can be isosceles or scalene.
In summary, while an equilateral triangle is unique with its perfect symmetry and equal sides and angles, other types of triangles exhibit a range of side lengths and angle measures, offering a rich variety of geometric properties and applications.

Equilateral Triangle Theorems
An equilateral triangle, due to its unique properties, satisfies several important theorems. These theorems not only highlight the symmetry and regularity of the equilateral triangle but also connect it with broader geometric principles.
- Angle Congruence Theorem
In an equilateral triangle, all three internal angles are equal. Since the sum of the internal angles in any triangle is 180 degrees, each angle in an equilateral triangle measures 60 degrees.
\[
\alpha = \beta = \gamma = \frac{180^\circ}{3} = 60^\circ
\] - Equilateral Triangle as an Isosceles Triangle
An equilateral triangle can be considered a special case of an isosceles triangle, where all three sides (and thus all three angles) are congruent. This allows the use of theorems applicable to isosceles triangles for equilateral triangles as well.
- Altitude, Median, and Angle Bisector Coincidence
In an equilateral triangle, the altitude, median, and angle bisector from any vertex coincide into a single line segment. This line not only bisects the angle and the opposite side but also represents the height of the triangle.
\[
h = \frac{\sqrt{3}}{2}a
\] - Congruence and Similarity Theorem
Any two equilateral triangles are similar, meaning they have the same shape but not necessarily the same size. This similarity comes from the fact that all their corresponding angles are equal (60 degrees), and their corresponding sides are proportional.
- Centroid, Circumcenter, Incenter, and Orthocenter Coincidence
In an equilateral triangle, the centroid, circumcenter, incenter, and orthocenter all coincide at a single point. This is a unique property of equilateral triangles not shared by other types of triangles.
- Euler Line
For an equilateral triangle, the Euler line, which typically connects the orthocenter, centroid, and circumcenter of a triangle, cannot be defined because these points coincide at a single point. Thus, there are infinitely many lines passing through this point.
- Area Theorem
The area of an equilateral triangle can be calculated using the formula:
\[
A = \frac{\sqrt{3}}{4}a^2
\]
where \(a\) is the length of a side. - Circumradius and Inradius
The circumradius (R) and inradius (r) of an equilateral triangle are related to the side length \(a\):
- Circumradius:
\[
R = \frac{a}{\sqrt{3}}
\]
- Inradius:
\[
r = \frac{\sqrt{3}}{6}a
\]
- Circumradius:
Applications in Real Life
Equilateral triangles play a significant role in various real-life applications due to their unique properties. Here are some prominent examples:
- Architecture and Construction: Equilateral triangles are used extensively in architectural designs and construction for their ability to evenly distribute weight and provide structural stability. For instance, the truss bridges are constructed using a framework of equilateral triangles to ensure strength and durability against heavy loads.
- Traffic Signs: Many traffic signs, particularly yield signs, are designed as equilateral triangles. The uniform angles and equal sides make them easily recognizable and effective for conveying important traffic information quickly.
- Electronic Devices: The play, rewind, and fast-forward buttons on remote controls and other electronic devices often use equilateral triangles. These symbols are universally understood, making device operation intuitive.
- Pyramids: The ancient Egyptian pyramids are a classic example of the use of equilateral triangles in monumental architecture. The triangular faces converge at a point, creating a stable and enduring structure.
- Sports Equipment: A billiard ball rack is another practical application, where the triangular shape efficiently holds the balls in position at the start of the game.
- Roof Design: Equilateral triangles are often used in the design of roofs, especially in regions with heavy snowfall. The shape ensures that snow slides off easily, preventing accumulation and potential damage.
- Tents: Traditional tents are often designed with equilateral triangular sides, providing a stable and wind-resistant structure ideal for camping and outdoor activities.
- Star Patterns: The Winter Triangle is an imaginary equilateral triangle formed by the stars Sirius, Betelgeuse, and Procyon. This triangle is easily identifiable in the night sky during winter months.
These examples demonstrate the versatility and practicality of equilateral triangles in various fields, from engineering and construction to everyday objects and natural phenomena.
Practice Problems and Solutions
Here are some practice problems to help you understand the concepts related to the perimeter of an equilateral triangle. Each problem is followed by a detailed solution.
Problem 1
An equilateral triangle has a side length of 8 cm. Calculate its perimeter.
Solution:
The formula for the perimeter \(P\) of an equilateral triangle is given by:
\[ P = 3a \]
where \(a\) is the side length of the triangle.
Substitute the given side length:
\[ P = 3 \times 8 \]
\[ P = 24 \, \text{cm} \]
Problem 2
Find the side length of an equilateral triangle if its perimeter is 45 cm.
Solution:
Using the perimeter formula \( P = 3a \), we can solve for \(a\):
\[ 45 = 3a \]
\[ a = \frac{45}{3} \]
\[ a = 15 \, \text{cm} \]
Problem 3
An equilateral triangle has a side length of \(12 \, \text{cm}\). Calculate its height.
Solution:
The height \(h\) of an equilateral triangle can be calculated using the formula:
\[ h = \frac{\sqrt{3}}{2} a \]
Substitute the given side length:
\[ h = \frac{\sqrt{3}}{2} \times 12 \]
\[ h = 6\sqrt{3} \, \text{cm} \]
Problem 4
The perimeter of an equilateral triangle is 60 cm. Calculate the area of the triangle.
Solution:
First, find the side length \(a\):
\[ P = 3a \]
\[ 60 = 3a \]
\[ a = 20 \, \text{cm} \]
Next, use the formula for the area \(A\) of an equilateral triangle:
\[ A = \frac{\sqrt{3}}{4} a^2 \]
Substitute the side length:
\[ A = \frac{\sqrt{3}}{4} \times 20^2 \]
\[ A = \frac{\sqrt{3}}{4} \times 400 \]
\[ A = 100\sqrt{3} \, \text{cm}^2 \]
Problem 5
Calculate the perimeter of an equilateral triangle with a height of \(6\sqrt{3} \, \text{cm}\).
Solution:
The height \(h\) is related to the side length \(a\) by the formula:
\[ h = \frac{\sqrt{3}}{2} a \]
Solve for \(a\):
\[ 6\sqrt{3} = \frac{\sqrt{3}}{2} a \]
\[ 6\sqrt{3} \times 2 = \sqrt{3} a \]
\[ 12\sqrt{3} = \sqrt{3} a \]
\[ 12 = a \]
Now, calculate the perimeter:
\[ P = 3a \]
\[ P = 3 \times 12 \]
\[ P = 36 \, \text{cm} \]
Frequently Asked Questions
-
What does the Perimeter of a Triangle Mean?
The perimeter of a triangle is the total distance around the edges of a triangle. In other words, it is the length of the boundary of the triangle.
-
How to Calculate the Perimeter of a Triangle?
To calculate the perimeter of a triangle, add the lengths of its sides. For example, if a triangle has sides \( a \), \( b \), and \( c \), then the perimeter of that triangle will be \( P = a + b + c \).
-
Calculate the Perimeter of a Right Triangle with Base as 3 cm and Height as 4 cm.
First, using the Pythagorean theorem, calculate the hypotenuse of the right triangle:
\( h = \sqrt{(\text{base})^2 + (\text{height})^2} \)
\( h = \sqrt{3^2 + 4^2} \)
\( h = \sqrt{9 + 16} \)
\( h = \sqrt{25} \)
\( h = 5 \, \text{cm} \)
So, the perimeter of the triangle = \( 3 + 4 + 5 = 12 \, \text{cm} \).
-
How to Calculate the Perimeter of a Scalene Triangle?
If \( x \), \( y \), and \( z \) are the sides of a scalene triangle, then its perimeter formula is given by:
Perimeter of a scalene triangle, \( P = x + y + z \, \text{units} \).
-
What is the Formula for the Perimeter of an Isosceles Triangle?
In an isosceles triangle, two sides are equal. The formula for the perimeter of an isosceles triangle is given as:
\( P = 2a + b \, \text{units} \)
where \( a \) is the measure of the equal sides of the triangle and \( b \) is the third side. -
What is the Formula for the Perimeter of an Equilateral Triangle?
In an equilateral triangle, all sides are equal. If the side length of an equilateral triangle is \( a \), the perimeter is:
\( P = 3a \, \text{units} \).
-
Calculate the Perimeter of an Equilateral Triangle if its Side Measures 5 cm.
Given the side length of the equilateral triangle is 5 cm, the perimeter is:
\( P = 3 \times 5 = 15 \, \text{cm} \).

Hướng dẫn cách tính chu vi của tam giác đều một cách dễ hiểu và nhanh chóng. Phù hợp cho học sinh và người mới bắt đầu.
Cách tìm chu vi của tam giác đều
READ MORE:
Hướng dẫn tính diện tích và chu vi của tam giác đều một cách chi tiết và dễ hiểu. Thích hợp cho học sinh và người học toán.
Cách tìm Diện tích và Chu vi của Tam giác Đều