Topic area of perimeter of square: Understanding the area and perimeter of a square is fundamental in geometry. This guide will help you grasp these essential concepts with clear formulas, step-by-step calculations, and practical examples. Whether you're a student or simply curious, this article will make learning about the area and perimeter of a square both easy and enjoyable.
Table of Content
- Understanding the Area and Perimeter of a Square
- Introduction to Square Geometry
- Definition of a Square
- Properties of a Square
- Formula for Perimeter
- Step-by-Step Calculation of Perimeter
- Real-World Examples of Perimeter Calculation
- Applications of Perimeter in Daily Life
- Formula for Area
- Step-by-Step Calculation of Area
- Real-World Examples of Area Calculation
- Applications of Area in Daily Life
- Comparing Perimeter and Area
- Common Misconceptions
- Practice Problems and Solutions
- Advanced Concepts Related to Squares
- Conclusion
- Further Reading and Resources
- YOUTUBE: Hướng dẫn chi tiết về cách tính diện tích và chu vi của hình vuông, giúp bạn nắm vững kiến thức cơ bản và ứng dụng trong thực tế.
Understanding the Area and Perimeter of a Square
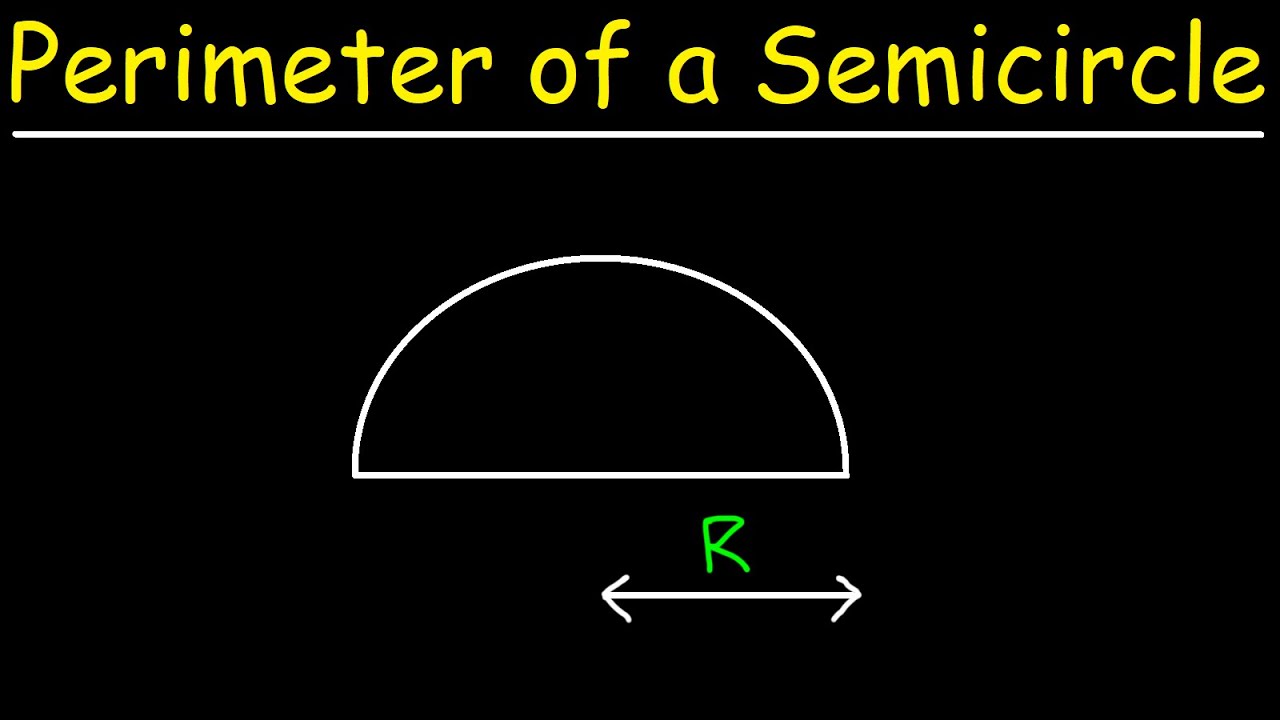
Perimeter of a Square
The perimeter of a square is the total length of all four sides. Since all sides of a square are equal in length, the formula for the perimeter \(P\) is:
\[ P = 4 \times a \]
where \(a\) is the length of one side of the square.
Example Calculation for Perimeter
If the side length \(a\) of a square is 5 units, then the perimeter is:
\[ P = 4 \times 5 = 20 \text{ units} \]
Area of a Square
The area of a square is the amount of space enclosed within its sides. The formula to calculate the area \(A\) is:
\[ A = a^2 \]
where \(a\) is the length of one side of the square.
Example Calculation for Area
If the side length \(a\) of a square is 5 units, then the area is:
\[ A = 5^2 = 25 \text{ square units} \]
Summary
- Perimeter of a square: \( P = 4 \times a \)
- Area of a square: \( A = a^2 \)
| Side Length (a) | Perimeter (P) | Area (A) |
|---|---|---|
| 1 | 4 | 1 |
| 2 | 8 | 4 |
| 3 | 12 | 9 |
| 4 | 16 | 16 |
| 5 | 20 | 25 |

READ MORE:
Introduction to Square Geometry
Geometry is a branch of mathematics that deals with shapes, sizes, and properties of space. One of the most fundamental shapes in geometry is the square. A square is a four-sided polygon, known as a quadrilateral, where all sides are of equal length and all angles are right angles (90 degrees).
Key characteristics of a square include:
- Four equal sides
- Four right angles
- Equal diagonals that bisect each other at right angles
These properties make squares highly symmetrical and easy to work with in various geometric calculations.
To better understand square geometry, let's look at two important aspects: perimeter and area.
Perimeter of a Square
The perimeter of a square is the total distance around the outside of the square. Since all four sides are equal in length, the perimeter \(P\) can be calculated using the formula:
\[ P = 4a \]
where \(a\) is the length of one side of the square.
For example, if the side length \(a\) is 6 units, the perimeter is:
\[ P = 4 \times 6 = 24 \text{ units} \]
Area of a Square
The area of a square is the amount of space enclosed within its sides. The area \(A\) is calculated using the formula:
\[ A = a^2 \]
where \(a\) is the length of one side of the square.
For example, if the side length \(a\) is 6 units, the area is:
\[ A = 6^2 = 36 \text{ square units} \]
Understanding these fundamental properties of squares is crucial for solving various geometric problems and applying these concepts in real-world scenarios.
Definition of a Square
A square is a special type of polygon known as a quadrilateral, which has four sides. What makes a square unique among quadrilaterals is its defining properties:
- Four Equal Sides: All sides of a square are of equal length. If the length of one side is denoted by \(a\), then the length of each of the four sides is also \(a\).
- Four Right Angles: Each internal angle in a square is a right angle, meaning it measures \(90^\circ\). This property ensures that a square is also a rectangle.
- Equal Diagonals: A square's diagonals are equal in length and bisect each other at right angles (90 degrees). The length of each diagonal can be calculated using the formula: \[ d = a\sqrt{2} \] where \(d\) is the length of the diagonal and \(a\) is the side length.
In summary, a square is characterized by its equal sides, right angles, and equal diagonals. These properties make squares highly symmetrical and a fundamental shape in geometry.
Let's break down these properties step-by-step:
- Side Length: Each side of a square is of the same length, denoted by \(a\).
- Angles: All internal angles are \(90^\circ\), making it a right-angled quadrilateral.
- Diagonals: The diagonals are equal in length, intersect at right angles, and their length is given by \(a\sqrt{2}\).
These fundamental properties of squares play a crucial role in many geometric calculations and applications.
| Property | Description | Formula |
|---|---|---|
| Sides | All four sides are equal in length. | \(a\) |
| Angles | Each internal angle is a right angle. | \(90^\circ\) |
| Diagonals | Diagonals are equal in length and bisect each other at right angles. | \(a\sqrt{2}\) |
Understanding the definition and properties of a square is essential for exploring more complex geometric concepts and solving related mathematical problems.
Properties of a Square
A square is a highly symmetrical shape with several unique properties that distinguish it from other geometric figures. Understanding these properties is essential for solving various mathematical problems and for applications in real-world scenarios. Here are the key properties of a square:
- Equal Sides: All four sides of a square are of equal length. If the length of one side is \(a\), then each side measures \(a\).
- Right Angles: A square has four right angles, meaning each internal angle is \(90^\circ\). This property ensures that a square is a type of rectangle.
- Equal Diagonals: The diagonals of a square are equal in length. Each diagonal divides the square into two congruent right-angled triangles. The length of the diagonal \(d\) can be calculated using the formula: \[ d = a\sqrt{2} \] where \(a\) is the length of a side.
- Diagonals Bisect at Right Angles: The diagonals of a square bisect each other at \(90^\circ\), forming four right angles at the point of intersection.
- Symmetry: A square has four lines of symmetry. These lines can be drawn by connecting the midpoints of opposite sides or by drawing the diagonals. Additionally, a square has rotational symmetry of order 4, meaning it looks the same after a rotation of \(90^\circ\), \(180^\circ\), \(270^\circ\), or \(360^\circ\).
- Perimeter: The perimeter \(P\) of a square is the total length of its boundaries. It can be calculated using the formula: \[ P = 4a \] where \(a\) is the side length.
- Area: The area \(A\) of a square is the amount of space enclosed within its sides. It is given by the formula: \[ A = a^2 \] where \(a\) is the side length.
Summary Table of Square Properties
| Property | Description | Formula/Value |
|---|---|---|
| Sides | All four sides are equal in length. | \(a\) |
| Angles | Each internal angle is a right angle. | \(90^\circ\) |
| Diagonals | Diagonals are equal in length and bisect each other at right angles. | \(a\sqrt{2}\) |
| Lines of Symmetry | Number of lines of symmetry. | 4 |
| Rotational Symmetry | Order of rotational symmetry. | 4 |
| Perimeter | Total length of the boundaries. | \(4a\) |
| Area | Space enclosed within the sides. | \(a^2\) |
By understanding these properties, one can easily solve problems related to squares in geometry and apply these concepts in various practical fields such as architecture, design, and more.
Formula for Perimeter
The perimeter of a square is a key geometric property that quantifies the total distance around the square. This is an essential calculation in various practical fields such as construction, design, and art.
Understanding the Formula:
The perimeter of a square can be calculated using a simple formula due to the equality of its four sides. The formula is:
\[ P = 4a \]
where \(P\) is the perimeter and \(a\) is the length of one side of the square.
Step-by-Step Calculation:
- Measure the Side Length: Determine the length of one side of the square. This length is represented by \(a\).
- Multiply by Four: Since all four sides of a square are equal, multiply the side length by 4 to get the total perimeter: \[ P = 4a \]
- Interpret the Result: The resulting value is the perimeter of the square, representing the total distance around it.
Example Calculation:
Consider a square with a side length of 5 units. To find the perimeter, apply the formula:
\[ P = 4 \times 5 = 20 \text{ units} \]
Visual Representation:
To better understand the formula, visualize a square with labeled sides:
| a | ||||
| a |
Since each side is of length \(a\), the perimeter is the sum of all four sides, \(a + a + a + a = 4a\).
Applications:
- Construction: Calculating the perimeter is essential for determining the amount of material needed for fencing, framing, and other construction projects.
- Design: In design and architecture, knowing the perimeter helps in planning layouts and ensuring symmetry.
- Art: Artists use the concept of perimeter to create balanced and proportionate works, especially in geometric art.
Summary Table
| Parameter | Description | Formula |
|---|---|---|
| Perimeter (P) | Total distance around the square. | \(P = 4a\) |
| Side Length (a) | Length of one side of the square. | \(a\) |
By understanding and applying the formula for the perimeter, \(P = 4a\), one can easily calculate the perimeter of any square, aiding in various mathematical and practical applications.

Step-by-Step Calculation of Perimeter
Calculating the perimeter of a square is straightforward because all four sides are of equal length. Here is a detailed, step-by-step guide to help you understand the process:
-
Identify the length of one side of the square. Let's denote this length as \( s \).
-
Recall the formula for the perimeter of a square:
\[
P = 4s
\]Where \( P \) is the perimeter and \( s \) is the length of one side.
-
Substitute the length of the side into the formula. For example, if the length of one side is 5 units, then:
\[
P = 4 \times 5
\] -
Perform the multiplication to find the perimeter:
\[
P = 20 \text{ units}
\] -
Therefore, the perimeter of a square with a side length of 5 units is 20 units.
Here is another example for further clarity:
-
Suppose the length of one side of the square is 7 units. Using the formula:
\[
P = 4s
\] -
Substitute the value of \( s \) (7 units) into the formula:
\[
P = 4 \times 7
\] -
Calculate the perimeter:
\[
P = 28 \text{ units}
\] -
Therefore, the perimeter of a square with a side length of 7 units is 28 units.
By following these steps, you can easily calculate the perimeter of any square as long as you know the length of one of its sides.
Real-World Examples of Perimeter Calculation
The perimeter of a square is an important measurement used in various real-world scenarios. Here are some detailed examples:
Example 1: Fencing a Garden
Suppose you have a square garden with each side measuring 10 meters, and you want to install a fence around it. To determine how much fencing material you need, you need to calculate the perimeter of the garden.
- Identify the length of one side of the square: \( s = 10 \text{ meters} \)
- Use the perimeter formula for a square: \( P = 4s \)
- Substitute the side length into the formula: \( P = 4 \times 10 = 40 \text{ meters} \)
You will need 40 meters of fencing material to enclose the garden.
Example 2: Creating a Square Tile Pathway
Imagine you are designing a square tile pathway in your backyard, and each side of the square pathway is 5 feet. To calculate the total length of the tiles needed to outline the pathway, you calculate the perimeter.
- Measure the side length of the square pathway: \( s = 5 \text{ feet} \)
- Apply the perimeter formula: \( P = 4s \)
- Insert the side length into the formula: \( P = 4 \times 5 = 20 \text{ feet} \)
Therefore, you need 20 feet of tiles to create the pathway's outline.
Example 3: Framing a Square Picture
Consider a square picture frame where each side is 8 inches long. To find out the length of the material needed to frame the picture, you calculate the perimeter of the square.
- Determine the length of one side of the square frame: \( s = 8 \text{ inches} \)
- Use the perimeter formula: \( P = 4s \)
- Plug in the side length: \( P = 4 \times 8 = 32 \text{ inches} \)
You will need 32 inches of framing material.
Example 4: Outlining a Square Sports Field
A square sports field has sides of 50 meters each. To find the length of the line needed to outline the field, you calculate its perimeter.
- Find the side length of the sports field: \( s = 50 \text{ meters} \)
- Apply the perimeter formula: \( P = 4s \)
- Substitute the side length into the formula: \( P = 4 \times 50 = 200 \text{ meters} \)
You need 200 meters of line to outline the sports field.
Example 5: Wrapping a Square Gift Box
You have a square gift box with each side measuring 12 inches. To determine the length of ribbon required to wrap around the box, you calculate the perimeter.
- Measure one side of the gift box: \( s = 12 \text{ inches} \)
- Use the perimeter formula: \( P = 4s \)
- Substitute the side length: \( P = 4 \times 12 = 48 \text{ inches} \)
You need 48 inches of ribbon to wrap around the gift box.
Applications of Perimeter in Daily Life
The concept of perimeter, which is the total length of the boundary of a two-dimensional shape, finds numerous applications in daily life. Here are some detailed examples:
-
Construction and Fencing
When constructing a house, garden, or any building, determining the perimeter is essential for purchasing materials such as fencing, boards for the walls, or molding for doors and windows.
For example, if you are building a rectangular garden that is 20 feet long and 30 feet wide, the perimeter would be:
\[
\text{Perimeter} = 2 \times (\text{Length} + \text{Width}) = 2 \times (20 + 30) = 100 \text{ feet}
\]This calculation ensures that you buy the correct amount of fencing to enclose the garden.
-
Interior Design
In interior design, knowing the perimeter of a room helps in determining the amount of materials needed for baseboards, crown molding, or even wallpaper and paint. For example, if a room is 15 feet long and 10 feet wide, the perimeter calculation is:
\[
\text{Perimeter} = 2 \times (\text{Length} + \text{Width}) = 2 \times (15 + 10) = 50 \text{ feet}
\] -
Landscaping
In landscaping, calculating the perimeter is crucial when designing pathways, flower beds, or any other feature that requires precise measurement for edging materials.
-
Sports Fields
For sports fields, the perimeter helps in planning the boundaries of the field, ensuring that it meets the standard dimensions for games and competitions. For example, a soccer field might have a perimeter calculation as follows if it is 100 meters long and 70 meters wide:
\[
\text{Perimeter} = 2 \times (100 + 70) = 340 \text{ meters}
\] -
Art and Framing
In the art world, calculating the perimeter is essential for creating frames for paintings and photographs. If you have a picture that is 8 inches by 10 inches, the perimeter would be:
\[
\text{Perimeter} = 2 \times (8 + 10) = 36 \text{ inches}
\]
Understanding the perimeter is not only fundamental in geometry but also immensely practical in various real-world scenarios, ensuring accuracy in construction, design, and daily measurements.
Formula for Area
The area of a square is the amount of space enclosed within its sides. It can be calculated using various methods depending on the known measurements. Here are the most common formulas:
-
Using the Side Length
The most straightforward way to calculate the area of a square is by using the length of one of its sides. The formula is:
\[ \text{Area} = s^2 \]
where \( s \) is the length of one side of the square.
Example: If the side length of a square is 5 cm, then the area is:
\[ \text{Area} = 5^2 = 25 \, \text{cm}^2 \]
-
Using the Diagonal
If the length of the diagonal is known, the area can be calculated using the formula:
\[ \text{Area} = \frac{d^2}{2} \]
where \( d \) is the length of the diagonal.
Example: If the diagonal length of a square is 10 cm, then the area is:
\[ \text{Area} = \frac{10^2}{2} = \frac{100}{2} = 50 \, \text{cm}^2 \]
-
Using the Perimeter
If the perimeter is known, the side length can first be calculated and then used to find the area. The formulas are:
\[ s = \frac{P}{4} \]
\[ \text{Area} = s^2 \]
where \( P \) is the perimeter of the square.
Example: If the perimeter of a square is 20 cm, then each side length is:
\[ s = \frac{20}{4} = 5 \, \text{cm} \]
Thus, the area is:
\[ \text{Area} = 5^2 = 25 \, \text{cm}^2 \]
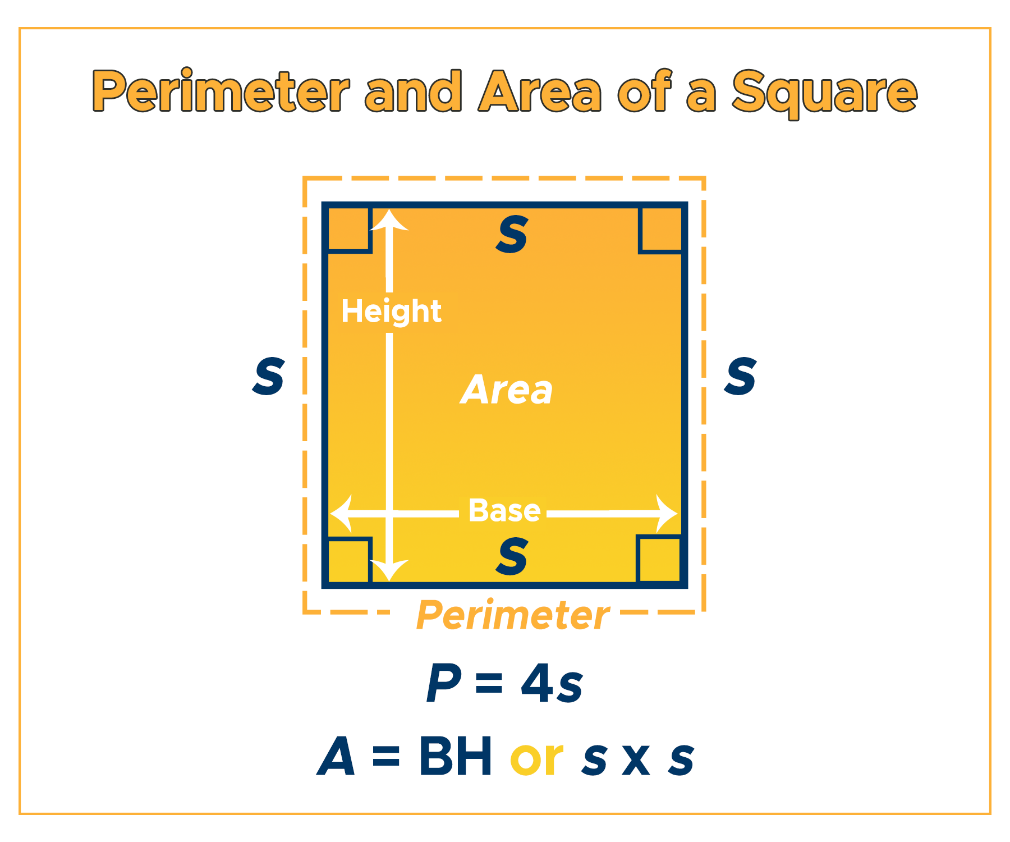
Step-by-Step Calculation of Area
To calculate the area of a square, you need to know the length of one of its sides. The formula for the area \( A \) of a square is given by:
\( A = a^2 \)
where \( a \) is the length of the side of the square. Below is a step-by-step guide to calculating the area of a square:
-
Determine the length of one side of the square.
For example, let's say the length of the side of the square is 5 units.
-
Substitute the side length into the area formula.
\( A = 5^2 \)
-
Perform the calculation.
\( A = 25 \, \text{square units} \)
Thus, the area of a square with a side length of 5 units is 25 square units.
Let's look at another example:
-
Determine the length of one side of the square.
Suppose the length of the side is 8 units.
-
Substitute the side length into the area formula.
\( A = 8^2 \)
-
Perform the calculation.
\( A = 64 \, \text{square units} \)
Therefore, the area of a square with a side length of 8 units is 64 square units.
This method can be applied to any square, regardless of the length of its sides. Just follow the steps: measure the side, square that measurement, and you have the area.
Real-World Examples of Area Calculation
Understanding the area of a square can be incredibly useful in various real-world situations. Here are some detailed examples that illustrate how to calculate the area in different contexts:
Example 1: Lawn Seeding
A homeowner wants to reseed their square lawn to ensure the grass grows evenly. The lawn measures 20 feet on each side.
- First, determine the length of one side of the square lawn: \( s = 20 \) feet.
- Use the area formula for a square: \( A = s \times s \).
- Calculate the area: \( A = 20 \times 20 = 400 \) square feet.
The homeowner will need enough seed to cover 400 square feet.
Example 2: Tiling a Floor
Imagine you are tiling a square kitchen floor that is 12 feet on each side. You need to know how many square feet of tiles to purchase.
- Measure the side length of the kitchen floor: \( s = 12 \) feet.
- Apply the area formula: \( A = s \times s \).
- Perform the calculation: \( A = 12 \times 12 = 144 \) square feet.
You will need 144 square feet of tiles to cover the entire kitchen floor.
Example 3: Painting a Wall
A painter needs to estimate the amount of paint required to cover a square wall that is 15 feet on each side.
- Identify the side length of the wall: \( s = 15 \) feet.
- Calculate the area using the formula: \( A = s \times s \).
- Find the area: \( A = 15 \times 15 = 225 \) square feet.
The painter will need enough paint to cover 225 square feet of wall space.
Example 4: Installing Solar Panels
A homeowner wants to install solar panels on their square rooftop, which measures 25 feet on each side.
- Measure the side length of the rooftop: \( s = 25 \) feet.
- Use the area formula: \( A = s \times s \).
- Calculate the area: \( A = 25 \times 25 = 625 \) square feet.
The rooftop can accommodate solar panels over an area of 625 square feet.
These examples highlight how calculating the area of a square is essential in various practical scenarios, from gardening and home improvement to energy efficiency projects.
Applications of Area in Daily Life
The concept of area is widely used in various real-life scenarios. Here are some detailed examples:
1. Construction and Architecture
In construction, the area is crucial for planning and designing spaces. For instance, determining the area of a room helps in selecting the right amount of flooring material.
- Example: To lay tiles in a room, you need to calculate the area of the floor. If a room is 12 feet by 15 feet, the area is \(12 \times 15 = 180 \text{ square feet}\).
2. Agriculture and Gardening
Farmers and gardeners use area calculations to determine the amount of seeds, fertilizers, and water required for their fields.
- Example: If a garden measures 20 feet by 30 feet, its area is \(20 \times 30 = 600 \text{ square feet}\). Knowing this helps in calculating the amount of fertilizer needed.
3. Real Estate
In real estate, the price of a property is often based on its area. Buyers and sellers calculate the area to assess property value.
- Example: A plot of land that is 50 feet by 40 feet has an area of \(50 \times 40 = 2000 \text{ square feet}\). If the price per square foot is $10, the total cost is \(2000 \times 10 = \$20,000\).
4. Painting
When painting walls or ceilings, knowing the area helps in estimating the amount of paint needed.
- Example: To paint a wall that is 10 feet high and 15 feet wide, the area is \(10 \times 15 = 150 \text{ square feet}\). If one gallon of paint covers 400 square feet, you will need \(150 / 400 = 0.375\) gallons, so purchasing one gallon is sufficient.
5. Interior Design
Interior designers calculate area to arrange furniture and decor efficiently within a space.
- Example: To place a rug in a living room measuring 10 feet by 12 feet, the area is \(10 \times 12 = 120 \text{ square feet}\). This helps in selecting a rug that fits the space appropriately.
6. HVAC (Heating, Ventilation, and Air Conditioning)
Calculating the area of a room is essential for determining the capacity of HVAC systems needed to heat or cool a space efficiently.
- Example: A room that is 14 feet by 14 feet has an area of \(14 \times 14 = 196 \text{ square feet}\). This measurement helps in selecting an HVAC unit with the right capacity.
7. Event Planning
For organizing events, knowing the area of a venue helps in planning the layout and ensuring enough space for attendees.
- Example: If an event hall is 50 feet by 80 feet, its area is \(50 \times 80 = 4000 \text{ square feet}\). This helps in arranging seating and other facilities.
These examples illustrate how understanding and calculating area can significantly impact efficiency and cost-effectiveness in various fields.
Comparing Perimeter and Area
Understanding the differences and relationships between perimeter and area is crucial in geometry. Both concepts measure different attributes of a shape, and knowing how to compare them can provide deeper insights into the properties of shapes.
Definitions
- Perimeter: The perimeter is the total length of the boundary of a shape. It is measured in linear units such as meters, centimeters, or inches.
- Area: The area is the amount of space enclosed within the boundary of a shape. It is measured in square units such as square meters, square centimeters, or square inches.
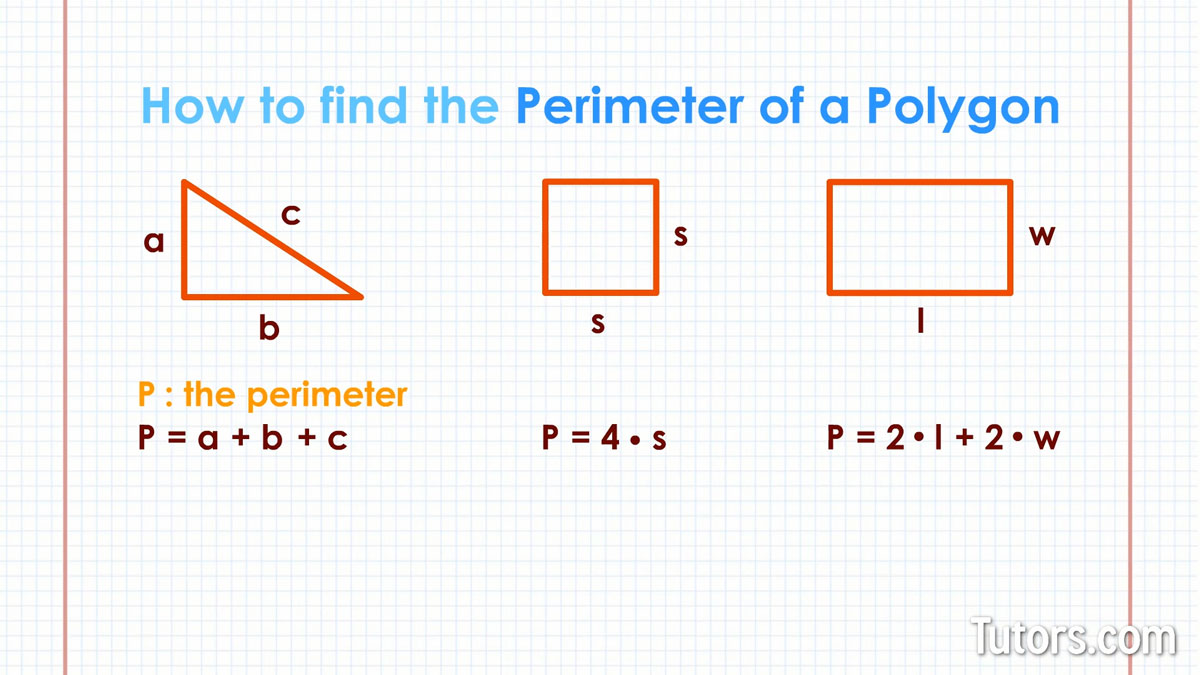
Formulas
| Shape | Perimeter Formula | Area Formula |
|---|---|---|
| Square | 4a | a^2 |
| Rectangle | 2(l + w) | l × w |
| Circle | 2πr | πr^2 |
| Triangle | a + b + c | 1/2 × b × h |
Key Differences
- Measurement Units: Perimeter is measured in linear units, while area is measured in square units.
- Conceptual Difference: Perimeter measures the boundary length, while area measures the enclosed space.
Example: Square
Consider a square with side length \( a = 5 \) units:
- Perimeter: \( P = 4a = 4 \times 5 = 20 \) units
- Area: \( A = a^2 = 5^2 = 25 \) square units
Comparison
For a given shape, perimeter and area can vary significantly:
- Two shapes with the same perimeter can have different areas.
- Two shapes with the same area can have different perimeters.
For example, a long, thin rectangle and a square might have the same perimeter but vastly different areas.
Applications
- Knowing the perimeter is useful for tasks such as fencing a garden or framing a picture.
- Knowing the area is essential for tasks such as laying carpet, tiling floors, or painting walls.
Understanding both perimeter and area is essential for solving real-world problems efficiently and effectively.

Common Misconceptions
Understanding the area and perimeter of a square is fundamental in geometry, but several common misconceptions can confuse learners. Below, we outline and clarify these misconceptions:
- Misconception: Area and perimeter are the same and interchangeable.
The area of a square measures the space inside it, calculated as where is the length of a side. The perimeter, however, measures the total length around the square, calculated as .
- Misconception: Square units mean the object is a square.
Square units are a way of measuring area and do not imply that the shape is a square. They simply represent the amount of space covered.
- Misconception: To find the area, you must use a "textbook issued" formula.
While the formula is standard for squares, understanding the concept of area as the number of unit squares that cover a surface is crucial. This helps in understanding area calculation for different shapes.
- Misconception: Area as a concept vs. area as a measurement.
Students often confuse the conceptual understanding of area with the procedural steps to calculate it. Emphasizing the conceptual aspect helps in applying area calculations in various contexts.
- Misconception: Area in 3-D or surface area in 3-D?
Area refers to 2-D space, whereas surface area refers to the total area covering a 3-D object. Clarifying this distinction is important to avoid confusion.
- Misconception: Including the wrong units with calculated area.
When calculating area, it's essential to use square units (e.g., square meters, square centimeters). Using linear units (e.g., meters) leads to incorrect interpretation.
By addressing these misconceptions, learners can develop a more accurate and comprehensive understanding of geometric concepts related to squares.
Practice Problems and Solutions
Here are some practice problems to help you understand the concepts of the area and perimeter of a square. Each problem is followed by a detailed solution.
-
Problem 1: The side of a square is 5 cm. Find the perimeter and area of the square.
Solution:
- Perimeter: \( P = 4a = 4 \times 5 \, \text{cm} = 20 \, \text{cm} \)
- Area: \( A = a^2 = 5^2 \, \text{cm}^2 = 25 \, \text{cm}^2 \)
-
Problem 2: The perimeter of a square is 32 cm. Find the length of one side and the area of the square.
Solution:
- Side length: \( P = 4a \rightarrow 32 \, \text{cm} = 4a \rightarrow a = \frac{32}{4} \, \text{cm} = 8 \, \text{cm} \)
- Area: \( A = a^2 = 8^2 \, \text{cm}^2 = 64 \, \text{cm}^2 \)
-
Problem 3: Find the perimeter of a square whose area is 49 cm².
Solution:
- Side length: \( A = a^2 \rightarrow 49 \, \text{cm}^2 = a^2 \rightarrow a = \sqrt{49} \, \text{cm} = 7 \, \text{cm} \)
- Perimeter: \( P = 4a = 4 \times 7 \, \text{cm} = 28 \, \text{cm} \)
-
Problem 4: The diagonal of a square is 10 cm. Find the area and perimeter of the square.
Solution:
- Side length: \( \text{Diagonal} = a\sqrt{2} \rightarrow 10 \, \text{cm} = a\sqrt{2} \rightarrow a = \frac{10}{\sqrt{2}} = \frac{10 \times \sqrt{2}}{2} = 5\sqrt{2} \, \text{cm} \)
- Area: \( A = a^2 = (5\sqrt{2})^2 \, \text{cm}^2 = 50 \, \text{cm}^2 \)
- Perimeter: \( P = 4a = 4 \times 5\sqrt{2} \, \text{cm} = 20\sqrt{2} \, \text{cm} \)
-
Problem 5: A square field has an area of 100 m². Calculate the side length and the cost to fence it at $5 per meter.
Solution:
- Side length: \( A = a^2 \rightarrow 100 \, \text{m}^2 = a^2 \rightarrow a = \sqrt{100} \, \text{m} = 10 \, \text{m} \)
- Perimeter: \( P = 4a = 4 \times 10 \, \text{m} = 40 \, \text{m} \)
- Cost of fencing: \( \text{Cost} = 40 \, \text{m} \times \$5/\text{m} = \$200 \)
These problems cover various aspects of calculating the area and perimeter of squares. Practice them to gain a better understanding and to prepare for exams.
Advanced Concepts Related to Squares
Understanding the advanced concepts related to squares involves exploring various geometric properties and relationships. Below are some advanced topics that provide deeper insights into the study of squares:
1. Diagonal Properties
The diagonals of a square have several interesting properties:
- The diagonals are equal in length.
- They bisect each other at right angles (90 degrees).
- Each diagonal divides the square into two congruent isosceles right triangles.
- The length of the diagonal \(d\) can be calculated using the Pythagorean theorem: \( d = a\sqrt{2} \), where \(a\) is the side length of the square.
2. Coordinate Geometry
Squares can be studied within the context of coordinate geometry:
- Consider a square with vertices at \( (0, 0) \), \( (a, 0) \), \( (a, a) \), and \( (0, a) \). This allows us to use algebraic methods to solve geometric problems.
- The equations of the lines forming the sides of the square can be derived and used for further calculations.
3. Transformation Geometry
Squares undergo various geometric transformations, including:
- Translation: Moving the square without rotating or changing its size.
- Rotation: Rotating the square around a point, often its center. A square rotated 90 degrees about its center will map onto itself.
- Reflection: Reflecting the square across a line (axis of symmetry). A square has four lines of symmetry.
- Scaling: Enlarging or reducing the square's size while preserving its shape.
4. Area and Perimeter Relationships
The relationships between the area and perimeter of a square can be explored in depth:
- The perimeter \(P\) of a square with side length \(a\) is \( P = 4a \).
- The area \(A\) of a square with side length \(a\) is \( A = a^2 \).
- These formulas can be used to derive other properties, such as the relationship between the side length and the diagonal.
5. Squares in Higher Dimensions
Extending the concept of squares to higher dimensions leads to:
- Cubes: In three dimensions, a square becomes a cube. Each face of a cube is a square.
- Hypercubes: In four or more dimensions, we have hypercubes (tesseracts in 4D), where each face is a cube.
6. Applications in Real Life
Advanced concepts related to squares have practical applications:
- Architecture: Designing buildings with square floor plans to maximize space efficiency.
- Engineering: Calculating load distributions in square plates and other structural elements.
- Computer Graphics: Using squares and their transformations to create and manipulate digital images.
7. Problem-Solving with Advanced Concepts
Applying these advanced concepts can solve complex geometric problems. For example:
- Using coordinate geometry to find the intersection points of lines within a square.
- Applying transformation principles to determine the new positions of a square after rotation or reflection.
- Using properties of diagonals to solve problems related to symmetry and distance.
These advanced concepts help deepen the understanding of squares and their properties, providing valuable tools for both theoretical and practical applications.
Conclusion
In this comprehensive guide, we've explored the fundamental concepts of square geometry, focusing specifically on the area and perimeter of a square. Understanding these concepts is crucial as they form the basis for more advanced geometric studies and have practical applications in various fields.
The perimeter of a square, calculated using the formula \(\text{Perimeter} = 4 \times \text{side}\), helps us determine the total distance around the square. This is particularly useful in tasks involving fencing, framing, and any project requiring precise boundary measurements.
Similarly, the area of a square, given by \(\text{Area} = \text{side}^2\), enables us to calculate the surface space within the square. This is essential in real-world applications such as determining the amount of material needed to cover a surface, planning layouts, and optimizing space usage.
By working through step-by-step calculations and exploring real-world examples, we've seen how these mathematical principles are applied in everyday situations. The comparison between perimeter and area highlights their distinct roles and the importance of understanding both for a well-rounded grasp of geometry.
We also addressed common misconceptions, reinforcing correct mathematical interpretations and providing clarity on frequently misunderstood concepts. The practice problems and solutions section offered hands-on experience, ensuring that learners can apply what they've learned confidently.
For those interested in delving deeper, advanced concepts related to squares were introduced, paving the way for further exploration and study. This guide serves as a solid foundation for anyone looking to master the basics of square geometry and beyond.
In conclusion, the study of the area and perimeter of a square is not only foundational but also highly practical. By mastering these concepts, you enhance your problem-solving skills and open up new opportunities for applying geometry in various aspects of life. Continue exploring, practicing, and applying these principles, and you'll find that your understanding of geometry will grow stronger and more intuitive.
We hope this guide has been informative and helpful. For further reading and resources, be sure to explore additional materials to expand your knowledge and proficiency in geometry.

Further Reading and Resources
To deepen your understanding of the area and perimeter of a square, here are some excellent resources and tools:
-
Khan Academy: Area and Perimeter
Offers a comprehensive collection of lessons, practice problems, and quizzes on the area and perimeter of various shapes, including squares. This is a great resource for both beginners and those looking to solidify their understanding.
-
Math Is Fun: Square Geometry
Provides clear explanations and interactive tools to explore the properties, area, and perimeter of squares. It's particularly useful for visual learners.
-
Cuemath: Perimeter of a Square
Includes detailed examples, step-by-step solutions, and practice problems to master the calculation of a square's perimeter and related concepts.
-
Byju's: Area and Perimeter
Offers extensive coverage on the area and perimeter of various geometric shapes, including squares. The site includes definitions, formulas, applications, and common questions to enhance your knowledge.
-
Omni Calculator: Area of a Square
Features a calculator to quickly find the area of a square given various parameters. It also explains the formulas used, making it a handy tool for quick computations and learning.
Hướng dẫn chi tiết về cách tính diện tích và chu vi của hình vuông, giúp bạn nắm vững kiến thức cơ bản và ứng dụng trong thực tế.
Cách tìm Diện tích và Chu vi của Hình vuông
READ MORE:
Hướng dẫn chi tiết về cách tính chu vi của hình vuông với Thầy J, giúp bạn nắm vững kiến thức cơ bản và ứng dụng trong thực tế.
Cách tìm Chu vi của Hình vuông | Toán học với Thầy J