Topic calculate perimeter of ellipse: Explore the intriguing world of elliptical geometry as we delve into the methods to calculate the perimeter of an ellipse, blending historical insights with practical mathematical applications.
Table of Content
- Can you calculate the perimeter of an ellipse accurately?
- Understanding Ellipses: Historical Background and Definitions
- Basic Ellipse Parameters: Major Axis, Minor Axis, and Eccentricity
- Common Perimeter Approximation Formulas
- Exact Perimeter Formulation: Integral Approach
- Practical Examples: Calculating Ellipse Perimeters
- YOUTUBE: 3 Ways to Calculate the Perimeter of an Ellipse and Derivation of the Formula
- Ellipse in Real Life: Applications and Examples
- Online Tools and Calculators for Ellipse Perimeter
- Advanced Topics: Eccentricity and its Role in Perimeter Calculation
Can you calculate the perimeter of an ellipse accurately?
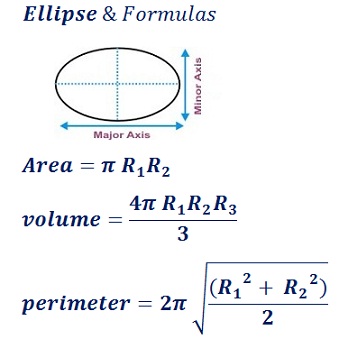
Unfortunately, calculating the perimeter of an ellipse accurately is not possible using a simple algebraic formula like in the case of finding the area of an ellipse. In fact, there is no exact formula for the perimeter of an ellipse. This means that any approach to calculate the perimeter will involve approximations or numerical methods, like integration.
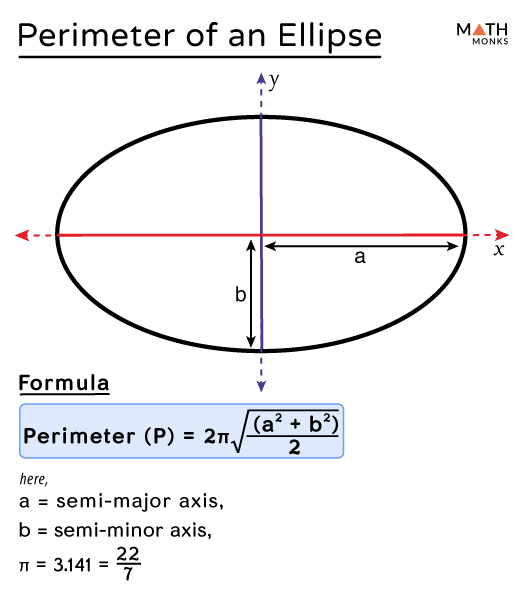
One common approximation for the perimeter of an ellipse is given by the formula: perimeter ≈ 2π√((a^2+b^2)/2), where \'a\' and \'b\' are the lengths of the major and minor axes of the ellipse. However, this formula is not exactly accurate and may introduce some degree of error.
If a more accurate result is desired, numerical methods can be employed. These methods involve breaking down the ellipse into smaller, manageable segments and calculating the sum of the lengths of these segments. However, this approach can be quite complex and time-consuming, as it requires a large number of calculations to achieve a reasonably accurate result.
Ultimately, it is important to understand that finding the exact perimeter of an ellipse is not straightforward and may require significant computation or approximation techniques.
READ MORE:
Understanding Ellipses: Historical Background and Definitions
An ellipse is a unique figure in geometry, related to conic sections, with an oval shape and fascinating properties. It differs from a circle in its shape and the way it\"s defined, making its study intriguing. Historically, ellipses have been a subject of study by prominent mathematicians and have applications in various real-world situations like planetary orbits and architectural designs.
- Definition and Basic Properties: An ellipse is described as the locus of points where the sum of distances from two fixed points (foci) is constant.
- Historical Significance: The study of ellipses dates back to ancient mathematicians. Notably, Kepler\"s discovery of planetary orbits being elliptical highlighted its astronomical importance.
- Geometric Construction: Formed by the intersection of a plane with a cone, an ellipse has two focal points, a center, major and minor axes, and an eccentricity less than one.
- Components of an Ellipse: Understanding the ellipse\"s components like the foci, axes, and eccentricity is crucial for comprehending its perimeter calculations.
- Real-Life Examples: Ellipses are not just theoretical constructs but have practical applications in various fields including astronomy and engineering.
Studying ellipses opens a gateway to understanding complex geometric shapes and their application in the real world, emphasizing the importance of their perimeter calculations.

Basic Ellipse Parameters: Major Axis, Minor Axis, and Eccentricity
The geometry of an ellipse is defined by three key parameters: the major axis, the minor axis, and the eccentricity. These elements are crucial in understanding the structure and properties of an ellipse, which in turn are essential for perimeter calculation.
- Major Axis: This is the longest diameter of an ellipse, stretching from one end to the other, passing through the center. It defines the longest distance across the ellipse.
- Minor Axis: The shortest diameter of the ellipse, the minor axis is perpendicular to the major axis and also passes through the center, defining the shortest distance across the ellipse.
- Eccentricity: A key parameter that measures the deviation of the ellipse from a circular shape. It is a non-negative number less than 1, where 0 represents a perfect circle and values approaching 1 indicate an increasingly elongated shape.
Understanding these parameters is fundamental in calculating the perimeter of an ellipse, as they directly influence the shape and size of the elliptical curve. The major and minor axes provide the necessary dimensions, while the eccentricity offers insight into the ellipse\"s overall shape.
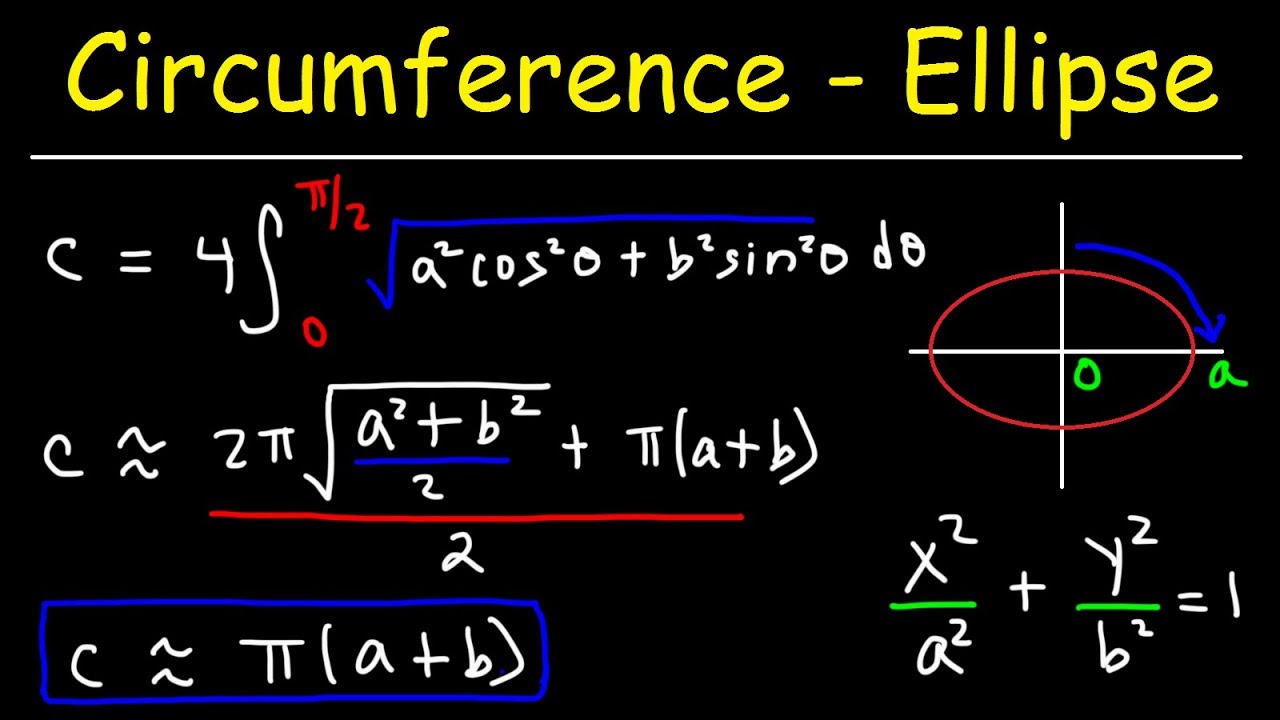
Common Perimeter Approximation Formulas
Calculating the exact perimeter of an ellipse involves complex mathematics, often requiring infinite series or integral calculus. However, there are several approximation formulas commonly used for practical purposes. These formulas provide a means to estimate the ellipse\"s perimeter with varying degrees of accuracy.
- Ramanujan\"s Approximations: These formulas, developed by the renowned mathematician Srinivasa Ramanujan, offer a balance between simplicity and accuracy. One popular version is P ≈ π [3(a + b) - √[(3a + b)(a + 3b)]].
- Infinite Series Formulas: These involve summing an infinite series of terms to approximate the perimeter. While they can provide high accuracy, they are more complex and require more computational power.
- Other Approximations: Various other formulas exist, each with its own level of simplicity and accuracy. These include simpler estimations like P ≈ π(a + b) [1 + (3h)/(10 + √(4 - 3h))], where h = ((a - b)/(a + b))^2.
These formulas are essential tools in various fields, from engineering to astronomy, where precise measurements of elliptical shapes are necessary. While exact calculations are complex, these approximations provide practical solutions for most applications.
Exact Perimeter Formulation: Integral Approach
The calculation of an ellipse\"s perimeter using the integral approach is a complex but precise method. This approach is necessary because there is no simple formula for accurately calculating the perimeter of an ellipse.
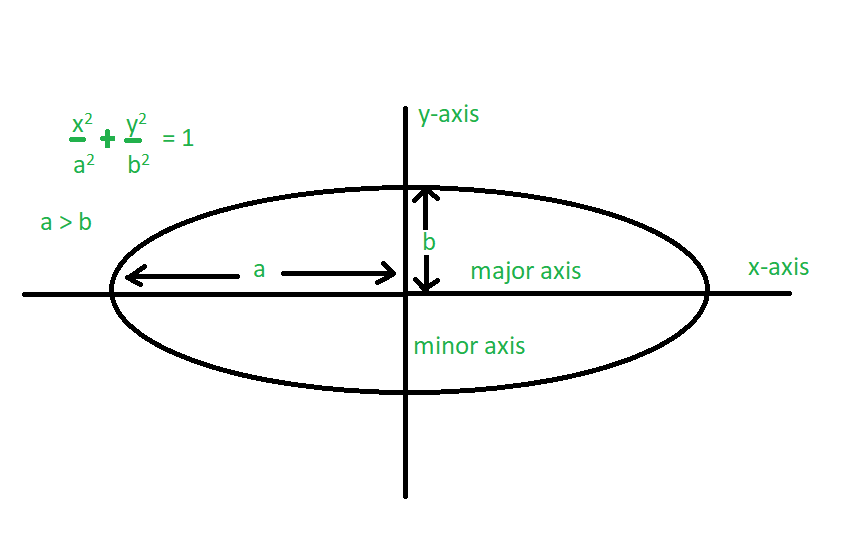
To start, consider an ellipse with a semi-major axis \"a\" and a semi-minor axis \"b\". The eccentricity \"e\" of the ellipse, which plays a crucial role in this calculation, is given by e = √(a² - b²)/a.
One way to calculate the perimeter is by using the arc length of a function. For an ellipse represented by the equation (x²/a²) + (y²/b²) = 1, this involves integrating over the interval [0, a] to find the perimeter in the first quadrant and then multiplying it by 4 to cover the entire ellipse. The integral for the first quadrant is expressed as:
- Perimeter of the ellipse in the first quadrant = 4 × ∫ from 0 to a √(1 + b²x²/(a²(a² - x²))) dx
Alternatively, the perimeter can also be calculated using parametric equations. The parametric equations for an ellipse are x = a cos θ and y = b sin θ. By integrating the square root of the sum of the squares of the derivatives of these parametric equations from 0 to π/2, and then multiplying by 4, we get the formula for the perimeter:
- P = 4a ∫ from 0 to π/2 √(1 - e² sin² θ) dθ
This integral approach, while exact, requires complex calculations and often the use of computational tools for practical applications.

_HOOK_
Practical Examples: Calculating Ellipse Perimeters
In this section, we will explore practical examples to calculate the perimeter of an ellipse using different methods, including approximation formulas and integral calculus.
Example 1: Using Approximation Formula
Suppose we have an ellipse with a semi-major axis of 12 units and a semi-minor axis of 11 units. To estimate the perimeter, we can use an approximation formula:
- Perimeter (P) ≈ π × (a + b)
- Here, a = 12 units, b = 11 units.
- So, P ≈ 3.14 × (12 + 11) = 72.22 units.
Example 2: Calculating Perimeter Using Integral Method
Consider an ellipse described by the equation (x²/25) + (y²/16) = 1. We can find its perimeter using integral calculus:
- First, identify a = 5 and b = 4 from the equation.
- Calculate the eccentricity, e = √(a² - b²) / a = √(25 - 16) / 5 = 3/5.
- Use the integral formula: P = 4a ∫ from 0 to π/2 √(1 - e² sin² θ) dθ.
- Compute the integral to find the perimeter, which can be approximated using a calculator.
Example 3: Using the Semi-Major and Semi-Minor Axes
For an ellipse with a semi-major axis of 10 cm and a semi-minor axis of 5 cm, the perimeter can be approximated as follows:
- Perimeter of ellipse = 2π √[(a² + b²)/2]
- Substituting a = 10 cm and b = 5 cm,
- The Perimeter ≈ 2 × 3.14 × √[(10² + 5²)/2] = 49.64 cm.
These examples provide a practical understanding of how to calculate the perimeter of an ellipse, highlighting both approximate and more exact methods.
3 Ways to Calculate the Perimeter of an Ellipse and Derivation of the Formula
Perimeter: Discover the secrets behind calculating the perimeter of any shape with this fascinating video! Learn useful tips and techniques to help you excel in geometry and tackle problem-solving with confidence. Watch now and unlock the wonders of perimeter!
How to Find the Circumference of an Ellipse
Circumference: Dive into the world of circles and unravel the mystery of circumference with this captivating video. Explore the relationship between radius, diameter, and circumference, and master the art of measuring circular objects. Get ready to be amazed by the beauty and simplicity of this essential geometry concept. Join us on this enlightening journey now!
Ellipse in Real Life: Applications and Examples
Ellipses are not just mathematical concepts; they have numerous applications in various fields. From architecture to technology, these geometric shapes play a vital role in our daily lives.
1. Architecture and Acoustics
Ellipses are widely used in architecture for their aesthetic appeal and unique properties. For instance, elliptical domes and ceilings, like those in St. Paul’s Cathedral, have special acoustic properties. In such structures, sound waves can travel between the two foci of the ellipse, enabling clear transmission of whispers across distances.
2. Technology and Engineering
In technology, elliptical lenses are crucial in optical devices such as telescopes and microscopes, focusing light more efficiently for better image quality. Elliptical shapes also strengthen structures in engineering, like bridges and arches, for better load distribution and stability.
3. Communications and Navigation
Elliptical shapes are integral in communication technologies. Satellite dishes, which are elliptically shaped, focus electromagnetic waves for better signal reception. Additionally, the principles of elliptical geometry are applied in GPS technology for accurate location tracking.
4. Medical Applications
The reflective properties of ellipses are used in medical procedures like lithotripsy, where shockwaves are focused to pulverize kidney stones without invasive surgery. This technique utilizes an ellipsoid-shaped device to direct energy precisely at the stones.
5. Exercise Equipment
Elliptical trainers in gyms simulate walking or running motions with a path that traces an ellipse. This design reduces the strain on the heart, making it an effective low-impact workout tool.
6. Astronomy and Space Exploration
Ellipses are fundamental in understanding celestial mechanics. Planetary orbits, including Earth’s path around the Sun, are elliptical, as described by Kepler\"s laws. This understanding is crucial in astronomy and space exploration.
7. Everyday Objects
Elliptical shapes are also found in everyday objects like elliptical mirrors, headlights and taillights of vehicles, and even in the design of some foods for aesthetic appeal.
From the grand scale of cosmic orbits to the intricate workings of optical devices, ellipses prove to be a shape of great importance and versatility in both nature and technology.

Online Tools and Calculators for Ellipse Perimeter
Calculating the perimeter of an ellipse can be complex, but several online tools and calculators make this task easier and more accurate. These calculators use various formulas, including Ramanujan\"s approximation, to provide precise results.
1. Ellipse Perimeter/Circumference Calculator
This calculator simplifies finding the perimeter (circumference) of an ellipse. Users need to enter the semi-major and semi-minor axis lengths, and the calculator employs Ramanujan\"s second approximation for accurate results. Additionally, it can also calculate the ellipse area.
2. Omni Calculator’s Ellipse Calculator
Omni Calculator\"s tool allows users to determine the basic parameters of an ellipse, including its center, vertices, foci, area, and perimeter. It also provides the eccentricity of the ellipse, a crucial factor in understanding its shape.
3. Owl Calculator’s Ellipse Perimeter Tool
This user-friendly tool automatically displays the perimeter of the ellipse upon entering the dimensions. It’s an excellent resource for quick calculations.
4. BYJU’S Ellipse Perimeter Calculator
BYJU\"S offers a free online tool for fast and accurate calculation of the ellipse\"s perimeter. It’s particularly useful for educational purposes.
5. Desmos Graphing Calculator
Desmos provides a graphical approach to calculating the ellipse perimeter. It’s an interactive tool ideal for those who prefer a visual method of learning.
6. Calculator.vg’s Ellipse Tools
With a focus on simplicity and speed, this online tool helps calculate the perimeter and area of an ellipse. It also explains the geometry of an ellipse and its properties.
These tools are invaluable for students, educators, and professionals who require accurate ellipse calculations without delving into complex manual computations.
READ MORE:
Advanced Topics: Eccentricity and its Role in Perimeter Calculation
The concept of eccentricity is pivotal in understanding the geometry of an ellipse and its perimeter calculation. Eccentricity (e) is a measure of how much an ellipse deviates from being circular. Mathematically, it\"s defined as the ratio of the distance from any point on the ellipse to a focus, and the distance from this point to the directrix.
Eccentricity is calculated using the formula: e = √(1 - (b²/a²)) for a horizontal ellipse and e = √(1 - (a²/b²)) for a vertical ellipse, where \"a\" is the semi-major axis and \"b\" is the semi-minor axis.
- The eccentricity of an ellipse ranges from 0 to 1. An eccentricity of 0 indicates a perfect circle, whereas an eccentricity close to 1 indicates a highly elongated ellipse.
- In the context of planetary orbits, eccentricity helps in understanding the elliptical paths of planets. For example, Earth with lower eccentricity has a nearly circular orbit, while Mercury with higher eccentricity has a more elongated path.
- In engineering, the eccentricity of elliptical gears influences their torque and rotational speed.
In terms of perimeter calculation, the eccentricity plays a role in determining the formula to be used. For ellipses with low eccentricity, simpler approximation formulas can be used. However, as the eccentricity increases, more complex formulas involving infinite series or elliptic integrals are required for accurate calculation.
Understanding the role of eccentricity in the geometry of an ellipse is essential for accurate calculation of its perimeter and for various practical applications in fields such as astronomy, engineering, and medical imaging.
Discover the intriguing world of ellipse perimeter calculations, a blend of geometric elegance and mathematical complexity. This journey from basic concepts to advanced topics illuminates how ellipses are not just theoretical constructs, but vital to understanding the real-world around us.