Topic area perimeter triangle: Unlock the secrets of triangles with our comprehensive guide on area and perimeter. Learn simple formulas, explore detailed examples, and gain confidence in calculating these essential properties of triangles. Perfect for students, teachers, and geometry enthusiasts looking to master the basics and apply them in real-world scenarios.
Table of Content
- Understanding the Area and Perimeter of a Triangle
- Introduction to Triangles
- Basic Properties of Triangles
- Types of Triangles
- Calculating the Perimeter of a Triangle
- Perimeter of Different Types of Triangles
- Calculating the Area of a Triangle
- Area Using Base and Height
- Heron's Formula for Area
- Trigonometric Method for Area Calculation
- Special Cases in Triangle Area Calculation
- Examples of Perimeter Calculations
- Examples of Area Calculations
- Common Mistakes in Triangle Calculations
- Applications of Triangle Area and Perimeter in Real Life
- Advanced Topics in Triangle Geometry
- Conclusion
- YOUTUBE:
Understanding the Area and Perimeter of a Triangle
Triangles are fundamental shapes in geometry, and understanding how to calculate their area and perimeter is essential. This guide provides formulas and examples to help you compute these properties.
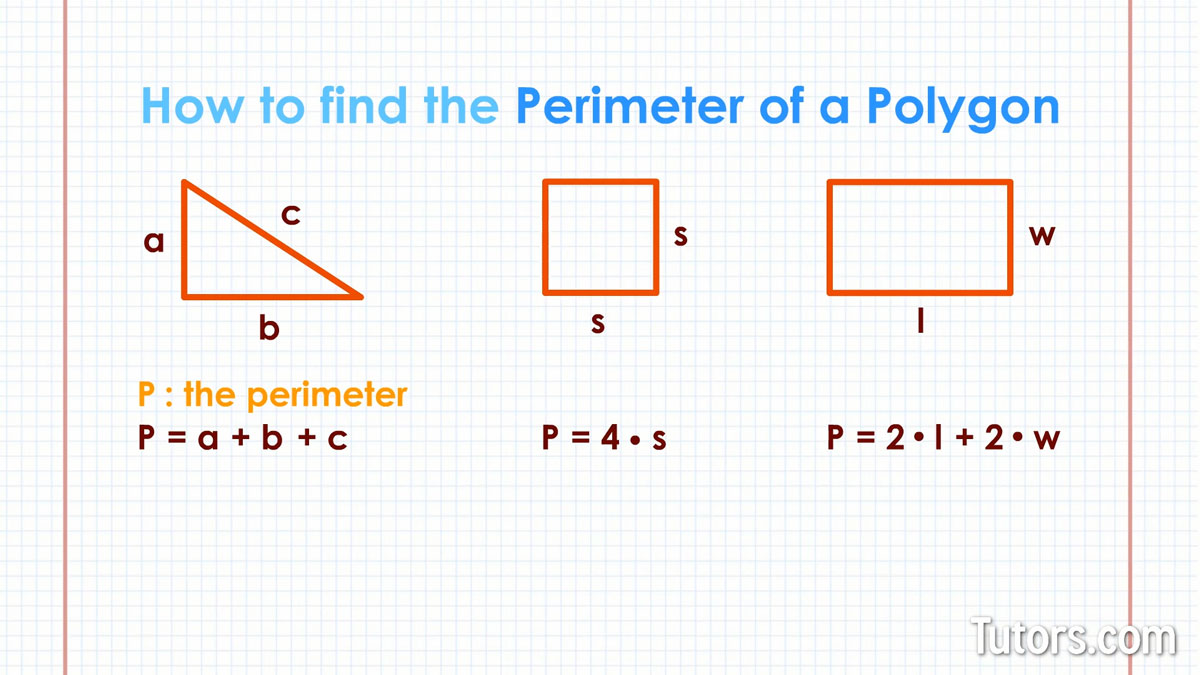
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its three sides. If a triangle has sides of lengths \( a \), \( b \), and \( c \), the perimeter \( P \) is given by:
\[ P = a + b + c \]
Area of a Triangle
There are multiple methods to calculate the area of a triangle, depending on the available information.
Using Base and Height
If you know the base \( b \) and the height \( h \) of the triangle, the area \( A \) is calculated as:
\[ A = \frac{1}{2} \times b \times h \]
Using Heron's Formula
If you know the lengths of all three sides, you can use Heron's formula. First, calculate the semi-perimeter \( s \):
\[ s = \frac{a + b + c}{2} \]
Then, the area \( A \) is given by:
\[ A = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \]
Using Trigonometry
If you know two sides and the included angle, the area can be calculated using trigonometry. For sides \( a \) and \( b \) with included angle \( \theta \), the area \( A \) is:
\[ A = \frac{1}{2} \times a \times b \times \sin(\theta) \]
Examples
Example 1: Perimeter
For a triangle with sides \( a = 5 \) cm, \( b = 7 \) cm, and \( c = 9 \) cm:
\[ P = 5 + 7 + 9 = 21 \text{ cm} \]
Example 2: Area using Base and Height
For a triangle with base \( b = 10 \) cm and height \( h = 6 \) cm:
\[ A = \frac{1}{2} \times 10 \times 6 = 30 \text{ cm}^2 \]
Example 3: Area using Heron's Formula
For a triangle with sides \( a = 5 \) cm, \( b = 7 \) cm, and \( c = 9 \) cm:
\[ s = \frac{5 + 7 + 9}{2} = 10.5 \text{ cm} \]
\]
\[ A = \sqrt{10.5 \times (10.5 - 5) \times (10.5 - 7) \times (10.5 - 9)} \approx 17.41 \text{ cm}^2 \]
Example 4: Area using Trigonometry
For a triangle with sides \( a = 8 \) cm, \( b = 6 \) cm, and included angle \( \theta = 60^\circ \):
\[ A = \frac{1}{2} \times 8 \times 6 \times \sin(60^\circ) = \frac{1}{2} \times 8 \times 6 \times \frac{\sqrt{3}}{2} \approx 20.78 \text{ cm}^2 \]
By mastering these formulas and methods, you can confidently calculate the area and perimeter of any triangle you encounter.
READ MORE:
Introduction to Triangles
Triangles are one of the most fundamental shapes in geometry. A triangle is a polygon with three edges and three vertices. It is a basic shape studied in various branches of mathematics and has significant applications in science, engineering, and art. Understanding triangles involves exploring their properties, types, and the methods to calculate their area and perimeter.
Key characteristics of triangles include:
- Three sides
- Three angles
- The sum of the interior angles is always \(180^\circ\)
Triangles can be classified based on their sides and angles:
- By Sides:
- Equilateral Triangle: All three sides are equal, and all angles are \(60^\circ\).
- Isosceles Triangle: Two sides are equal, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
- By Angles:
- Acute Triangle: All three angles are less than \(90^\circ\).
- Right Triangle: One angle is exactly \(90^\circ\).
- Obtuse Triangle: One angle is greater than \(90^\circ\).
Understanding the area and perimeter of triangles is crucial for solving many geometric problems. Here's a brief overview:
- Perimeter: The perimeter of a triangle is the sum of the lengths of its three sides. If the sides are \(a\), \(b\), and \(c\), then the perimeter \(P\) is given by: \[ P = a + b + c \]
- Area: The area of a triangle can be calculated in several ways, depending on the information available:
- Using base \(b\) and height \(h\): \[ A = \frac{1}{2} \times b \times h \]
- Using Heron's Formula when all sides \(a\), \(b\), and \(c\) are known: \[ s = \frac{a + b + c}{2} \] \[ A = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \]
- Using trigonometry when two sides and the included angle \( \theta \) are known: \[ A = \frac{1}{2} \times a \times b \times \sin(\theta) \]
By understanding these basic properties and formulas, you can tackle a wide range of problems involving triangles with confidence and precision.
Basic Properties of Triangles
Triangles are essential shapes in geometry with unique properties that differentiate them from other polygons. Understanding these properties helps in various geometric calculations and proofs. Here are the fundamental properties of triangles:
- Three Sides and Three Angles: A triangle has three sides and three interior angles.
- Sum of Interior Angles: The sum of the interior angles of a triangle is always \(180^\circ\).
- Types of Triangles:
- Equilateral Triangle: All three sides are equal, and all three angles are \(60^\circ\).
- Isosceles Triangle: Two sides are equal, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
- Acute Triangle: All three angles are less than \(90^\circ\).
- Right Triangle: One angle is exactly \(90^\circ\).
- Obtuse Triangle: One angle is greater than \(90^\circ\).
- Perimeter: The perimeter of a triangle is the sum of the lengths of its three sides: \[ P = a + b + c \]
- Area: The area of a triangle can be calculated in different ways:
- Using base \(b\) and height \(h\): \[ A = \frac{1}{2} \times b \times h \]
- Using Heron's Formula, where \(s\) is the semi-perimeter: \[ s = \frac{a + b + c}{2} \] \[ A = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \]
- Using trigonometry for two sides and included angle \(\theta\): \[ A = \frac{1}{2} \times a \times b \times \sin(\theta) \]
Other important properties include:
- Exterior Angles: The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
- Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.
- Centroid: The point where the three medians (lines drawn from each vertex to the midpoint of the opposite side) intersect. It divides each median into a ratio of 2:1.
- Orthocenter: The point where the three altitudes (perpendiculars drawn from each vertex to the opposite side) intersect.
- Circumcenter: The point where the perpendicular bisectors of the sides intersect. It is the center of the circumscribed circle (circumcircle) around the triangle.
- Incenter: The point where the angle bisectors intersect. It is the center of the inscribed circle (incircle) within the triangle.
By mastering these properties, you can deepen your understanding of triangle geometry and solve complex problems with confidence.
Types of Triangles
Triangles can be classified based on the lengths of their sides and the measures of their angles. Understanding these classifications is essential for solving geometric problems and applying various formulas. Here are the different types of triangles:
Classification by Sides
- Equilateral Triangle: All three sides are equal in length, and all three interior angles are \(60^\circ\).
Properties:
- All sides are congruent: \( a = b = c \)
- All angles are congruent: \( \angle A = \angle B = \angle C = 60^\circ \)
- Area: \[ A = \frac{\sqrt{3}}{4} \times a^2 \]
- Isosceles Triangle: Two sides are equal in length, and the angles opposite these sides are equal.
Properties:
- Two sides are congruent: \( a = b \)
- Two angles are congruent: \( \angle A = \angle B \)
- Area: \[ A = \frac{1}{2} \times b \times h \]
- Scalene Triangle: All three sides and all three angles are different.
Properties:
- No sides are congruent: \( a \neq b \neq c \)
- No angles are congruent: \( \angle A \neq \angle B \neq \angle C \)
- Area (using Heron's Formula): \[ s = \frac{a + b + c}{2} \] \[ A = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \]
Classification by Angles
- Acute Triangle: All three interior angles are less than \(90^\circ\).
Properties:
- All angles are acute: \( \angle A < 90^\circ, \angle B < 90^\circ, \angle C < 90^\circ \)
- Right Triangle: One interior angle is exactly \(90^\circ\).
Properties:
- One right angle: \( \angle C = 90^\circ \)
- The side opposite the right angle is the hypotenuse: \( c \)
- Pythagorean Theorem: \[ a^2 + b^2 = c^2 \]
- Area: \[ A = \frac{1}{2} \times a \times b \]
- Obtuse Triangle: One interior angle is greater than \(90^\circ\).
Properties:
- One obtuse angle: \( \angle C > 90^\circ \)
By recognizing these types of triangles and their properties, you can apply appropriate formulas and theorems to solve various geometric problems effectively.
Calculating the Perimeter of a Triangle
The perimeter of a triangle is the total length around the triangle. It is calculated by summing the lengths of all three sides. Knowing how to calculate the perimeter is fundamental in geometry and helps in solving various problems related to triangles.
To calculate the perimeter of a triangle, follow these steps:
- Identify the lengths of the sides:
- Label the sides of the triangle as \( a \), \( b \), and \( c \).
- Use the perimeter formula:
The formula to calculate the perimeter \( P \) of a triangle is:
\[ P = a + b + c \] - Sum the lengths of the sides:
- Add the values of \( a \), \( b \), and \( c \) to get the perimeter.
Here are some examples to illustrate the calculation:
Example 1: Equilateral Triangle
An equilateral triangle has all three sides of equal length. Suppose each side is \( 6 \) cm. The perimeter \( P \) is:
Example 2: Isosceles Triangle
An isosceles triangle has two sides of equal length. Suppose the lengths of the sides are \( a = 5 \) cm, \( b = 5 \) cm, and \( c = 8 \) cm. The perimeter \( P \) is:
Example 3: Scalene Triangle
A scalene triangle has all sides of different lengths. Suppose the lengths of the sides are \( a = 3 \) cm, \( b = 4 \) cm, and \( c = 5 \) cm. The perimeter \( P \) is:
By following these steps and using the perimeter formula, you can easily determine the perimeter of any triangle, whether it is equilateral, isosceles, or scalene. This knowledge is useful in various applications of geometry, from solving theoretical problems to practical uses in fields such as engineering and architecture.

Perimeter of Different Types of Triangles
Calculating the perimeter of a triangle involves summing the lengths of its sides. The approach is straightforward but varies slightly depending on the type of triangle: equilateral, isosceles, or scalene. Here's how to calculate the perimeter for each type of triangle:
Equilateral Triangle
An equilateral triangle has all three sides of equal length.
- Identify the length of one side:
- Let \( a \) be the length of each side.
- Use the perimeter formula: \[ P = a + a + a = 3a \]
For example, if each side is \( 6 \) cm:
Isosceles Triangle
An isosceles triangle has two sides of equal length and a third side of a different length.
- Identify the lengths of the sides:
- Let \( a \) be the length of the two equal sides and \( b \) be the length of the third side.
- Use the perimeter formula: \[ P = a + a + b = 2a + b \]
For example, if the equal sides are \( 5 \) cm each and the third side is \( 8 \) cm:
Scalene Triangle
A scalene triangle has all three sides of different lengths.
- Identify the lengths of the sides:
- Let \( a \), \( b \), and \( c \) be the lengths of the three sides.
- Use the perimeter formula: \[ P = a + b + c \]
For example, if the sides are \( 3 \) cm, \( 4 \) cm, and \( 5 \) cm:
These formulas and methods can be applied to determine the perimeter of any triangle, regardless of its type. Knowing how to calculate the perimeter accurately is essential for solving more complex geometric problems and understanding the properties of triangles.
Calculating the Area of a Triangle
To calculate the area of a triangle, there are several methods available depending on the information provided. The most common methods include using the base and height, Heron's formula, and trigonometric functions. Each method is useful in different scenarios, and understanding these methods is essential for accurate calculations.
1. Area Using Base and Height
The formula to calculate the area of a triangle using its base and height is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
Steps to calculate:
- Identify the base (b) of the triangle.
- Measure the height (h) perpendicular to the base.
- Apply the formula \( \frac{1}{2} \times b \times h \) to find the area.
2. Heron's Formula
Heron's formula is used when the lengths of all three sides of the triangle are known. The formula is:
\[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
where \( s \) is the semi-perimeter of the triangle, calculated as:
\[ s = \frac{a + b + c}{2} \]
Steps to calculate:
- Measure the lengths of all three sides (a, b, and c).
- Calculate the semi-perimeter \( s \) using \( s = \frac{a + b + c}{2} \).
- Apply Heron's formula \( \sqrt{s(s-a)(s-b)(s-c)} \) to find the area.
3. Trigonometric Method
This method is used when two sides and the included angle are known. The formula is:
\[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(C) \]
Steps to calculate:
- Identify the lengths of two sides (a and b) and the included angle (C).
- Calculate the sine of the angle \( \sin(C) \).
- Apply the formula \( \frac{1}{2} \times a \times b \times \sin(C) \) to find the area.
Understanding these methods and knowing when to apply each one ensures accurate and efficient calculations of the area of a triangle in various scenarios.
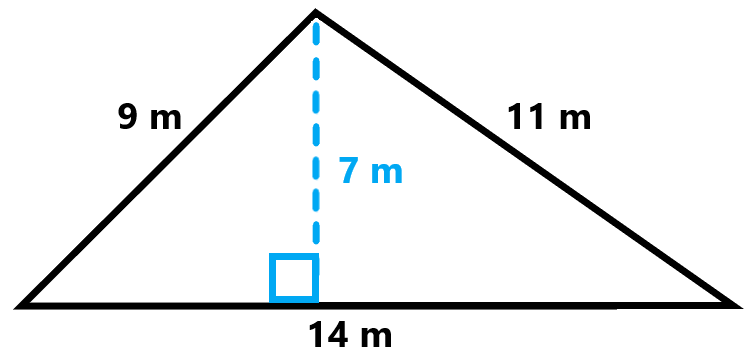
Area Using Base and Height
The area of a triangle can be calculated using the formula:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
This formula is applicable to all types of triangles as long as the base and the corresponding height are known. Here is a step-by-step guide to calculate the area:
- Identify the Base and Height: The base (\(b\)) can be any side of the triangle, but the height (\(h\)) must be the perpendicular distance from the base to the opposite vertex.
- Apply the Formula: Once the base and height are identified, plug them into the formula.
Let's look at an example to illustrate this:
- Consider a triangle with a base of 8 cm and a height of 5 cm.
- Using the formula: \( \text{Area} = \frac{1}{2} \times 8 \, \text{cm} \times 5 \, \text{cm} \)
- Simplifying this, we get \( \text{Area} = \frac{1}{2} \times 40 \, \text{cm}^2 = 20 \, \text{cm}^2 \)
The calculation is straightforward and provides a reliable way to determine the area of a triangle when the base and height are known.
In summary, the formula \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \) is a simple and effective method to find the area of a triangle, making it a fundamental concept in geometry.
Heron's Formula for Area
Heron's formula is a useful method for calculating the area of a triangle when the lengths of all three sides are known. The formula is named after Hero of Alexandria, an ancient Greek engineer and mathematician.
To use Heron's formula, follow these steps:
- Calculate the semi-perimeter of the triangle. The semi-perimeter, \( s \), is half of the perimeter of the triangle and is given by:
\[ s = \frac{a + b + c}{2} \]
where \( a \), \( b \), and \( c \) are the lengths of the sides of the triangle. - Use the semi-perimeter to calculate the area, \( A \), of the triangle using the following formula:
\[ A = \sqrt{s(s - a)(s - b)(s - c)} \]
Let's go through an example to illustrate this process:
Example: Calculate the area of a triangle with side lengths 5, 6, and 7 units.
- First, find the semi-perimeter \( s \):
\[ s = \frac{5 + 6 + 7}{2} = 9 \]
- Next, use Heron's formula to find the area:
\[ A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} \]
\[ A = \sqrt{9 \cdot 4 \cdot 3 \cdot 2} \]
\[ A = \sqrt{216} \]
\[ A = 6 \sqrt{6} \approx 14.7 \, \text{square units} \]
Heron's formula is especially handy for triangles where the height is not easily determined, such as scalene triangles where all sides are of different lengths.
This method simplifies the calculation and avoids the need for complex trigonometric functions or constructing perpendicular heights.
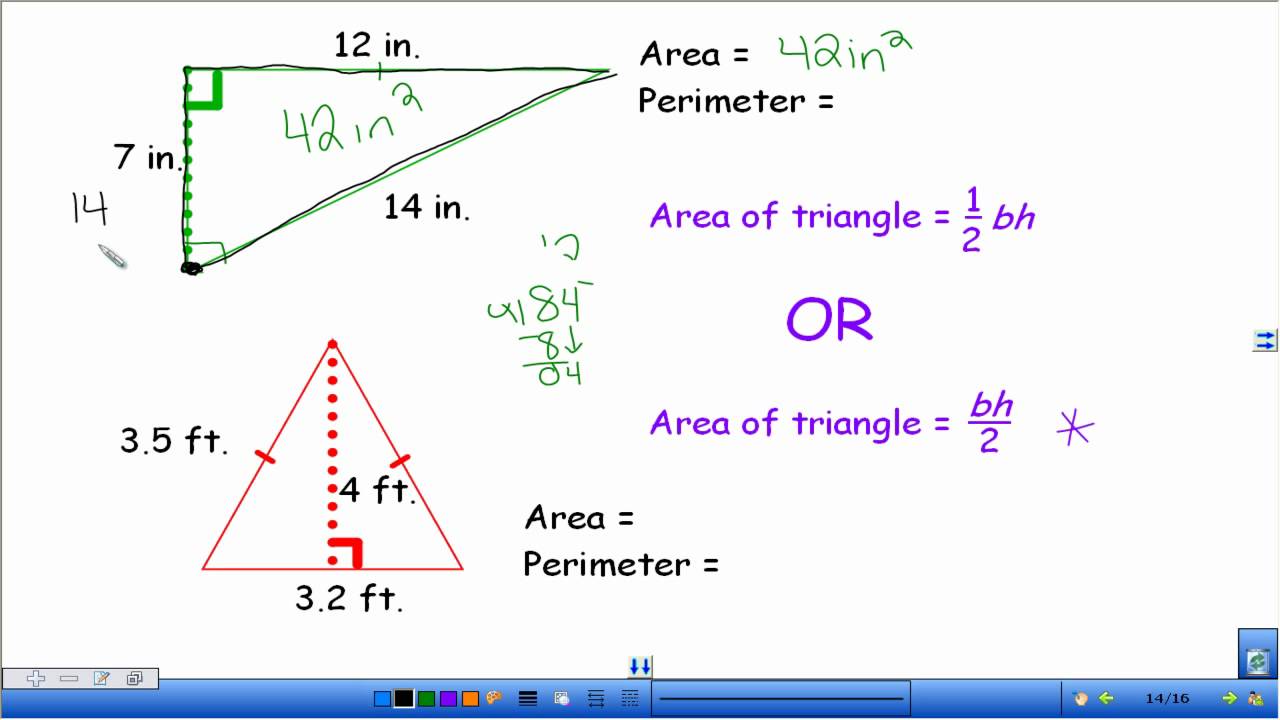
Trigonometric Method for Area Calculation
The trigonometric method for calculating the area of a triangle is particularly useful when the height is not known, but the lengths of two sides and the included angle are available. This method leverages the sine function to determine the area efficiently.
The formula for the area (\(K\)) of a triangle using trigonometry is given by:
\( K = \frac{1}{2} \times a \times b \times \sin(C) \)
Here, \(a\) and \(b\) are the lengths of two sides of the triangle, and \(C\) is the included angle between them.
The steps to calculate the area using this method are as follows:
-
Identify the sides and angle: Determine the lengths of two sides of the triangle and the included angle between them. Label these sides as \(a\) and \(b\) and the angle as \(C\). -
Calculate the sine of the angle: Use a calculator to find the value of \(\sin(C)\). -
Plug the values into the formula: Substitute the side lengths and the sine of the angle into the formula:
\( K = \frac{1}{2} \times a \times b \times \sin(C) \) -
Compute the area: Perform the multiplication to find the area of the triangle.
Example 1:
Consider a triangle with sides \(a = 8 \, \text{cm}\) and \(b = 10 \, \text{cm}\), and an included angle \(C = 45^\circ\). To find the area:
- Calculate the sine of \(45^\circ\): \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \)
- Use the formula: \( K = \frac{1}{2} \times 8 \, \text{cm} \times 10 \, \text{cm} \times \frac{\sqrt{2}}{2} \)
- Compute the result: \( K = 20 \sqrt{2} \, \text{cm}^2 \)
Example 2:
Consider a triangle with sides \(a = 6 \, \text{cm}\) and \(b = 9 \, \text{cm}\), and an included angle \(C = 30^\circ\). To find the area:
- Calculate the sine of \(30^\circ\): \( \sin(30^\circ) = 0.5 \)
- Use the formula: \( K = \frac{1}{2} \times 6 \, \text{cm} \times 9 \, \text{cm} \times 0.5 \)
- Compute the result: \( K = 13.5 \, \text{cm}^2 \)
This trigonometric method is an efficient and accurate way to calculate the area of a triangle when the height is not directly available, making it a versatile tool in various geometric applications.
Special Cases in Triangle Area Calculation
There are several special cases in triangle area calculations where unique formulas and methods are applied to simplify the process:
1. Right Triangle
In a right triangle, one of the angles is \(90^\circ\), which allows the use of a simplified formula for area calculation:
Given the two legs of the right triangle, \(a\) and \(b\):
\[ \text{Area} = \frac{1}{2} \times a \times b \]
For example, if \(a = 3\) and \(b = 4\):
\[ \text{Area} = \frac{1}{2} \times 3 \times 4 = 6 \]
2. Equilateral Triangle
An equilateral triangle has all three sides equal and all angles are \(60^\circ\). The formula for the area of an equilateral triangle with side length \(s\) is:
\[ \text{Area} = \frac{\sqrt{3}}{4} s^2 \]
For example, if \(s = 6\):
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \approx 15.59 \]
3. Isosceles Triangle
In an isosceles triangle, two sides are of equal length. The formula for the area can be derived using the Pythagorean theorem:
Given the equal sides \(a\) and the base \(b\):
\[ \text{Area} = \frac{1}{2} b \sqrt{a^2 - \left(\frac{b}{2}\right)^2} \]
For example, if \(a = 5\) and \(b = 6\):
\[ \text{Area} = \frac{1}{2} \times 6 \times \sqrt{5^2 - \left(\frac{6}{2}\right)^2} = 3 \times \sqrt{25 - 9} = 3 \times \sqrt{16} = 3 \times 4 = 12 \]
4. Heron's Formula
For any triangle with sides \(a\), \(b\), and \(c\), Heron's formula can be used when the height is unknown:
First, calculate the semi-perimeter \(s\):
\[ s = \frac{a + b + c}{2} \]
Then, the area is given by:
\[ \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \]
For example, if \(a = 7\), \(b = 8\), and \(c = 9\):
\[ s = \frac{7 + 8 + 9}{2} = 12 \]
\[ \text{Area} = \sqrt{12(12-7)(12-8)(12-9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.83 \]
5. Area of a Triangle Given Two Sides and the Included Angle
If two sides and the included angle are known, the area can be calculated using the sine function:
Given sides \(a\) and \(b\) with the included angle \(\theta\):
\[ \text{Area} = \frac{1}{2} ab \sin(\theta) \]
For example, if \(a = 5\), \(b = 7\), and \(\theta = 60^\circ\):
\[ \text{Area} = \frac{1}{2} \times 5 \times 7 \times \sin(60^\circ) = \frac{35}{2} \times \frac{\sqrt{3}}{2} = \frac{35 \sqrt{3}}{4} \approx 15.14 \]
Examples of Perimeter Calculations
Calculating the perimeter of a triangle involves summing the lengths of all its sides. Below are examples of perimeter calculations for different types of triangles:
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula for its perimeter is:
\[ P = 3a \]
where \( a \) is the length of a side.
For example, if each side of an equilateral triangle is 10 cm:
\[ P = 3 \times 10 = 30 \, \text{cm} \]
Isosceles Triangle
An isosceles triangle has two sides of equal length. The formula for its perimeter is:
\[ P = 2a + b \]
where \( a \) is the length of the equal sides, and \( b \) is the base.
For example, if the equal sides are 10 cm each and the base is 20 cm:
\[ P = 2 \times 10 + 20 = 40 \, \text{cm} \]
Scalene Triangle
A scalene triangle has all sides of different lengths. The formula for its perimeter is:
\[ P = a + b + c \]
where \( a \), \( b \), and \( c \) are the lengths of the sides.
For example, if the sides are 5 cm, 7 cm, and 10 cm:
\[ P = 5 + 7 + 10 = 22 \, \text{cm} \]
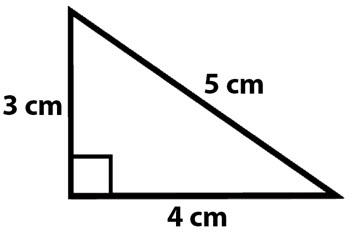
Right Triangle
A right triangle has one 90-degree angle. The sides are the base (\( b \)), the height (\( h \)), and the hypotenuse (\( c \)). The formula for its perimeter is:
\[ P = b + h + c \]
For example, if the base is 3 cm, the height is 4 cm, and using the Pythagorean theorem, the hypotenuse is:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \, \text{cm} \]
Then the perimeter is:
\[ P = 3 + 4 + 5 = 12 \, \text{cm} \]
These examples demonstrate how to calculate the perimeter of various types of triangles. Practice with different sets of side lengths to reinforce your understanding.
Examples of Area Calculations
Calculating the area of a triangle can be done using various methods depending on the known parameters. Here are some examples to illustrate different methods:
Example 1: Using Base and Height
Consider a triangle with a base (b) of 6 units and a height (h) of 4 units. The area (A) is calculated as follows:
- Formula: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Calculation: \( A = \frac{1}{2} \times 6 \times 4 \)
- Result: \( A = 12 \, \text{square units} \)
Example 2: Using Heron's Formula
For a triangle with sides of lengths 5 units, 6 units, and 7 units, the area can be calculated using Heron's formula:
- Step 1: Calculate the semi-perimeter (s):
- \( s = \frac{a + b + c}{2} \)
- Substitute values: \( s = \frac{5 + 6 + 7}{2} = 9 \, \text{units} \)
- Step 2: Apply Heron's formula:
- Formula: \( A = \sqrt{s(s-a)(s-b)(s-c)} \)
- Calculation: \( A = \sqrt{9(9-5)(9-6)(9-7)} \)
- Simplify: \( A = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \, \text{square units} \)
Example 3: Using Trigonometry
If two sides and the included angle are known, the area can be found using the formula involving sine. Consider a triangle with sides of 7 units and 8 units, and an included angle of 30 degrees:
- Formula: \( A = \frac{1}{2}ab \sin C \)
- Calculation: \( A = \frac{1}{2} \times 7 \times 8 \times \sin(30^\circ) \)
- Result: \( A = \frac{1}{2} \times 7 \times 8 \times 0.5 = 14 \, \text{square units} \)
Example 4: Area of an Equilateral Triangle
For an equilateral triangle with side length (a) of 5 units, the area is calculated as:
- Formula: \( A = \frac{\sqrt{3}}{4} a^2 \)
- Calculation: \( A = \frac{\sqrt{3}}{4} \times 5^2 \)
- Result: \( A \approx 10.83 \, \text{square units} \)
Example 5: Area of a Right Triangle
For a right triangle with legs of 3 units and 4 units, the area is calculated as:
- Formula: \( A = \frac{1}{2} \times \text{leg}_1 \times \text{leg}_2 \)
- Calculation: \( A = \frac{1}{2} \times 3 \times 4 \)
- Result: \( A = 6 \, \text{square units} \)
Example 6: Special Case - Triangle Inside a Rectangle
If a triangle is formed by slicing a rectangle diagonally, each of the resulting triangles will have an area that is half of the area of the rectangle. For a rectangle with length 8 units and width 6 units:
- Area of the rectangle: \( 8 \times 6 = 48 \, \text{square units} \)
- Area of each triangle: \( \frac{1}{2} \times 48 = 24 \, \text{square units} \)
These examples illustrate how the area of a triangle can be calculated using different methods depending on the given information. Understanding these methods allows for accurate and efficient computation of areas in various scenarios.

Common Mistakes in Triangle Calculations
When calculating the area and perimeter of triangles, several common mistakes can occur. Being aware of these errors can help ensure more accurate results. Here are some of the most frequent mistakes and how to avoid them:
1. Incorrect Variable Assignment
One of the most frequent errors is using incorrect variables in your calculations. This can happen when mislabeling sides or angles, leading to incorrect results. Always double-check that each variable correctly represents the side or angle intended.
2. Misapplication of Formulas
Applying the wrong formula to calculate area or perimeter is another common mistake. For example:
- Area Formula: Using the formula
\( \frac{1}{2} \times \text{base} \times \text{height} \)is only valid when the base and height are perpendicular. - Heron's Formula: Forgetting to calculate the semi-perimeter first:
\( s = \frac{a + b + c}{2} \), where \( a \), \( b \), and \( c \) are the side lengths.
3. Measurement Errors
Inaccurate measurements of sides or angles can significantly affect calculations. To avoid this, use precise tools and double-check measurements.
4. Wrong Units
Using inconsistent units (e.g., mixing centimeters and meters) can lead to incorrect results. Always ensure that all measurements are in the same unit before performing calculations.
5. Misinterpretation of Given Data
Misreading the problem or misinterpreting given data, such as assuming a right angle where there isn't one, can lead to errors. Carefully read the problem and verify all given data before starting calculations.
6. Arithmetic Mistakes
Simple arithmetic mistakes, such as incorrect addition or multiplication, can distort your results. Double-check your calculations or use a calculator for accuracy.
7. Incorrect Use of Trigonometric Functions
When using trigonometric functions, ensure you are using the correct function for the given angles and sides. Common errors include:
- Using sine instead of cosine or vice versa.
- Incorrect angle measurements (degrees vs. radians).
8. Rounding Errors
Rounding intermediate results too early can lead to significant inaccuracies. Keep as many decimal places as possible during calculations and round off only in the final step.
9. Lack of Focus
Distractions and lack of focus can lead to careless mistakes. Stay concentrated, work in a quiet environment, and take breaks if needed to maintain accuracy.
10. Diagram Errors
Incorrectly drawn diagrams can lead to wrong assumptions and errors in calculations. Always ensure your diagrams accurately represent the problem.
By being mindful of these common mistakes and taking steps to avoid them, you can improve the accuracy of your triangle calculations.
Applications of Triangle Area and Perimeter in Real Life
The concepts of triangle area and perimeter are utilized in various real-life applications, ranging from architecture to astronomy. Below are some detailed examples of how these geometric principles are applied:
- Construction and Architecture
Buildings and Monuments: Triangular shapes are commonly used in the design of structures like the Eiffel Tower and other architectural marvels. These structures rely on the principles of triangles to ensure stability and strength.
Bridges: Many bridges use triangular trusses to distribute weight and provide support. This use of triangles helps maintain the structural integrity of the bridges.
Home Construction: Calculating the area and perimeter of triangular sections is crucial in determining the amount of materials needed, such as roofing and flooring.
- Land and Agriculture
Land Measurement: When buying or selling land, especially in irregular shapes, calculating the area can involve breaking the land into triangles. This helps in precise measurement and valuation.
Irrigation Planning: Understanding the perimeter and area of triangular fields helps in designing efficient irrigation systems.
- Transportation
Triangular Traffic Signs: Triangular shapes are used in traffic signs to convey warnings and important information effectively.
- Recreational and Daily Life
Food Design: Triangular shapes are common in foods like sandwiches, pizza slices, and snacks. Calculating the area and perimeter can be useful in packaging and serving sizes.
Sports Fields: Some sports fields, like certain sections of a track or soccer goal areas, use triangular dimensions to mark boundaries and zones.
- Science and Astronomy
Astronomical Calculations: Triangles are used in astronomy to measure distances between stars and planets. The area and perimeter calculations help in mapping celestial objects and their movements.
- Art and Design
Graphic Design: Triangular shapes are often used in graphic design and computer graphics to create visually appealing and structurally sound images.
Fashion: Designers use triangles in patterns and cutting fabrics, ensuring precision and aesthetic appeal in clothing and accessories.
Understanding the applications of triangle area and perimeter not only enhances mathematical skills but also provides practical insights into how these concepts are integral to various fields and everyday activities.
Advanced Topics in Triangle Geometry
In this section, we explore some advanced concepts in triangle geometry that go beyond the basics. These topics are crucial for a deeper understanding of geometric properties and relationships.
1. Euler's Line
In any triangle, the orthocenter, centroid, and circumcenter are collinear and lie on a line known as Euler's line. The centroid divides Euler's line into two segments, where the distance from the centroid to the circumcenter is twice the distance from the centroid to the orthocenter.
To visualize this, consider a triangle with vertices \(A\), \(B\), and \(C\). Let \(H\) be the orthocenter, \(G\) be the centroid, and \(O\) be the circumcenter. Then, \(H\), \(G\), and \(O\) lie on Euler's line.
2. Nine-Point Circle
The nine-point circle, also known as the Euler circle, passes through nine significant points of a triangle: the midpoint of each side, the foot of each altitude, and the midpoint of the segment from each vertex to the orthocenter. The center of the nine-point circle lies on Euler's line and is the midpoint of the segment joining the orthocenter and circumcenter.
3. Ceva's Theorem
Ceva's Theorem provides a criterion for three cevians (lines from a vertex to the opposite side) to be concurrent. For a triangle \(ABC\), let \(D\), \(E\), and \(F\) be points on \(BC\), \(CA\), and \(AB\), respectively. The cevians \(AD\), \(BE\), and \(CF\) are concurrent if and only if:
\[\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1\]
4. Menelaus's Theorem
Menelaus's Theorem is used to determine when three points on the sides of a triangle (or their extensions) are collinear. For a triangle \(ABC\) with points \(D\), \(E\), and \(F\) on \(BC\), \(CA\), and \(AB\), respectively, the points are collinear if:
\[\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1\]
5. Inversions in Circle
Inversion is a transformation that maps points inside a given circle to the outside and vice versa. This technique can simplify many geometric problems by transforming complex configurations into simpler ones. For a given circle with center \(O\) and radius \(R\), the inversion of a point \(P\) is a point \(P'\) such that:
\[OP \cdot OP' = R^2\]
6. The Poincaré Disk
The Poincaré disk model is used in hyperbolic geometry, where the entire hyperbolic plane is represented inside a disk. The model helps visualize hyperbolic lines, which appear as arcs of circles orthogonal to the boundary circle of the disk.
Conclusion
These advanced topics in triangle geometry reveal the richness and depth of geometric principles. Understanding these concepts provides a solid foundation for further exploration in both theoretical and applied mathematics.
Conclusion
In this comprehensive guide, we've delved deeply into the concepts of triangle area and perimeter, exploring their definitions, formulas, and real-life applications. Understanding these fundamental geometric properties not only enhances your mathematical skills but also broadens your perspective on how geometry is integrated into various aspects of our daily lives.
From the basic properties of triangles to the advanced methods of calculating their area and perimeter, we've covered a wide array of topics. We learned how to apply simple formulas for quick calculations and also tackled more complex scenarios involving Heron's formula and trigonometric methods.
Throughout the journey, we've highlighted common mistakes to avoid and provided practical examples to ensure clarity and confidence in solving triangle-related problems. Whether you're a student, teacher, or simply a math enthusiast, the knowledge gained here will serve as a solid foundation for further exploration into the fascinating world of geometry.
Remember, the key to mastering triangle calculations lies in understanding the principles behind the formulas and practicing their application in various contexts. Keep experimenting with different types of triangles and scenarios to reinforce your learning and uncover new insights.
As you continue your mathematical journey, always stay curious and open to discovering the endless possibilities that geometry offers. With a strong grasp of triangle area and perimeter, you're well-equipped to tackle more advanced topics and real-life challenges with confidence and precision.
Thank you for embarking on this educational adventure. We hope this guide has been both informative and inspiring, encouraging you to further your exploration of mathematics and its many wonders.
Cách Tìm Diện Tích và Chu Vi của Tam Giác
READ MORE:
Cách Tìm Diện Tích và Chu Vi của Tam Giác | Toán với Thầy J