Topic area and perimeter problems: Discover how to solve area and perimeter problems with ease! This comprehensive guide covers essential formulas, step-by-step examples, and advanced techniques. Whether you’re a student or just looking to brush up on your math skills, this article will help you master the concepts of area and perimeter for various shapes and applications.
Table of Content
- Area and Perimeter Problems
- Introduction to Area and Perimeter
- Basic Formulas for Common Shapes
- Calculating Area and Perimeter of Rectangles
- Solving Problems Involving Squares
- Understanding Circle Area and Circumference
- Triangles: Area and Perimeter Calculations
- Composite Shapes: Combining Areas and Perimeters
- Advanced Problem-Solving Techniques
- Word Problems Involving Area and Perimeter
- Real-World Applications of Area and Perimeter
- Tips for Solving Complex Area and Perimeter Problems
- Common Mistakes and How to Avoid Them
- Interactive Tools and Practice Problems
- Conclusion and Summary
- YOUTUBE:
Area and Perimeter Problems
Understanding the concepts of area and perimeter is essential for solving various geometry problems. Here, we explore different types of area and perimeter problems along with their solutions.
Basic Formulas
Let's start with the fundamental formulas for area and perimeter:
- Rectangle:
- Area: \( A = l \times w \)
- Perimeter: \( P = 2(l + w) \)
- Square:
- Area: \( A = s^2 \)
- Perimeter: \( P = 4s \)
- Circle:
- Area: \( A = \pi r^2 \)
- Circumference: \( C = 2 \pi r \)
- Triangle:
- Area: \( A = \frac{1}{2} \times b \times h \)
- Perimeter: Sum of all sides \( P = a + b + c \)
Example Problems and Solutions
1. Finding the Area of a Rectangle
Problem: Calculate the area of a rectangle with a length of 8 meters and a width of 5 meters.
Solution: Using the formula \( A = l \times w \), we have:
\[ A = 8 \times 5 = 40 \text{ square meters} \]
2. Calculating the Perimeter of a Square
Problem: Determine the perimeter of a square with a side length of 6 meters.
Solution: Using the formula \( P = 4s \), we get:
\[ P = 4 \times 6 = 24 \text{ meters} \]
3. Area and Circumference of a Circle
Problem: Find the area and circumference of a circle with a radius of 7 meters.
Solution: Using the formulas \( A = \pi r^2 \) and \( C = 2 \pi r \), we calculate:
\[ A = \pi \times 7^2 = 49 \pi \approx 153.94 \text{ square meters} \]
\[ C = 2 \pi \times 7 = 14 \pi \approx 43.98 \text{ meters} \]
4. Perimeter of a Triangle
Problem: Find the perimeter of a triangle with sides measuring 3 meters, 4 meters, and 5 meters.
Solution: Sum the lengths of all sides:
\[ P = 3 + 4 + 5 = 12 \text{ meters} \]
5. Area of a Triangle
Problem: Calculate the area of a triangle with a base of 10 meters and a height of 5 meters.
Solution: Using the formula \( A = \frac{1}{2} \times b \times h \), we have:
\[ A = \frac{1}{2} \times 10 \times 5 = 25 \text{ square meters} \]
Advanced Problems
Let's delve into more complex problems involving composite shapes and variable dimensions.
6. Area and Perimeter of a Composite Shape
Problem: Find the area and perimeter of an L-shaped figure made by joining two rectangles, one with dimensions 4 meters by 2 meters and another with dimensions 3 meters by 5 meters.
Solution: Calculate the area and perimeter of each rectangle, then combine them:
\[ A_1 = 4 \times 2 = 8 \text{ square meters} \]
\[ A_2 = 3 \times 5 = 15 \text{ square meters} \]
\[ A_{\text{total}} = A_1 + A_2 = 8 + 15 = 23 \text{ square meters} \]
Perimeter involves subtracting the shared sides and adding all other sides:
\[ P = 4 + 2 + 5 + 3 + 1 = 15 \text{ meters} \]
7. Variable Dimensions
Problem: A rectangle has a length that is twice its width. If the perimeter is 36 meters, find the dimensions and area of the rectangle.
Solution: Let the width be \( w \) and the length be \( 2w \). Using the perimeter formula \( P = 2(l + w) \), we have:
\[ 36 = 2(2w + w) \]
\[ 36 = 6w \]
\[ w = 6 \text{ meters} \]
So, the length \( l \) is \( 2 \times 6 = 12 \text{ meters} \).
\[ A = l \times w = 12 \times 6 = 72 \text{ square meters} \]
Conclusion
Understanding and applying the formulas for area and perimeter allows us to solve a wide range of problems in geometry. Practice with different shapes and complexities to master these concepts.
READ MORE:
Introduction to Area and Perimeter
Area and perimeter are fundamental concepts in geometry, essential for understanding the dimensions and boundaries of various shapes. Whether dealing with simple rectangles or complex composite shapes, mastering these concepts is crucial. This introduction will guide you through the basic definitions, formulas, and practical applications of area and perimeter.
- Area refers to the amount of space inside a shape. It's measured in square units and varies depending on the shape's dimensions. For example, the area of a rectangle is calculated using the formula:
- Perimeter is the total distance around the boundary of a shape. It’s measured in linear units. The perimeter of a rectangle is found by adding up the lengths of all its sides:
\[ \text{Area} = \text{Length} \times \text{Width} \]
For a circle, the area is determined by:
\[ \text{Area} = \pi r^2 \]
\[ \text{Perimeter} = 2(\text{Length} + \text{Width}) \]
For a circle, the perimeter, also known as the circumference, is given by:
\[ \text{Circumference} = 2 \pi r \]
To fully understand these concepts, let's break them down step by step:
- Identifying Shapes: Recognize the shape you are dealing with—whether it's a rectangle, square, triangle, or circle. This identification is the first step in applying the correct formulas for area and perimeter.
- Applying Formulas: Use the appropriate formulas based on the shape identified. Each shape has specific formulas that make calculating area and perimeter straightforward.
- Units of Measurement: Always pay attention to the units used. Area is expressed in square units (e.g., square meters), while perimeter is in linear units (e.g., meters).
- Practical Applications: Understanding how to calculate area and perimeter is useful in various real-world scenarios, such as determining the amount of paint needed for a wall (area) or the length of fencing required for a garden (perimeter).
With these basics in mind, you are ready to explore and solve area and perimeter problems across different types of shapes. This foundation will also help in tackling more advanced geometric problems involving composite shapes and irregular boundaries.
Basic Formulas for Common Shapes
Understanding the basic formulas for calculating the area and perimeter of common shapes is essential for solving geometry problems. Here, we will cover the fundamental formulas for rectangles, squares, circles, and triangles.
- Rectangle:
- Area:
- Perimeter:
- Square:
- Area:
- Perimeter:
- Circle:
- Area:
- Circumference (Perimeter):
- Triangle:
- Area:
- Perimeter:
The area and perimeter of a rectangle depend on its length (\( l \)) and width (\( w \)). The formulas are:
\[ \text{Area} = l \times w \]
\[ \text{Perimeter} = 2(l + w) \]
A square is a special case of a rectangle where all sides are equal in length (\( s \)). The formulas are simplified as:
\[ \text{Area} = s^2 \]
\[ \text{Perimeter} = 4s \]
A circle is defined by its radius (\( r \)), the distance from its center to any point on its circumference. The formulas are:
\[ \text{Area} = \pi r^2 \]
\[ \text{Circumference} = 2 \pi r \]
For triangles, the formulas vary depending on the type, but for a right triangle or any triangle with a known base (\( b \)) and height (\( h \)), the formulas are:
\[ \text{Area} = \frac{1}{2} \times b \times h \]
The perimeter is the sum of all its sides. For a triangle with sides \( a \), \( b \), and \( c \):
\[ \text{Perimeter} = a + b + c \]
These basic formulas form the foundation for understanding more complex geometric problems. Let’s explore each shape in more detail with practical examples:
- Rectangle Example: To find the area of a rectangle with a length of 8 meters and a width of 5 meters, use:
- Square Example: For a square with a side length of 4 meters, the perimeter is:
- Circle Example: Given a circle with a radius of 3 meters, the area is:
- Triangle Example: For a triangle with a base of 6 meters and a height of 4 meters, the area is:
\[ \text{Area} = 8 \times 5 = 40 \, \text{square meters} \]
\[ \text{Perimeter} = 4 \times 4 = 16 \, \text{meters} \]
\[ \text{Area} = \pi \times 3^2 = 9 \pi \approx 28.27 \, \text{square meters} \]
\[ \text{Area} = \frac{1}{2} \times 6 \times 4 = 12 \, \text{square meters} \]
By mastering these formulas, you can tackle a wide range of area and perimeter problems effectively and efficiently.
Calculating Area and Perimeter of Rectangles
Rectangles are one of the most common shapes encountered in geometry. Understanding how to calculate their area and perimeter is crucial for solving various real-world problems. This guide will take you through the steps needed to compute these values effectively.
Step-by-Step Calculation
- Identify the Length and Width:
To begin, determine the length (\( l \)) and width (\( w \)) of the rectangle. These dimensions can be measured or provided in a problem statement. In a rectangle, opposite sides are equal in length, so you only need to measure one pair of adjacent sides.
- Calculate the Area:
The area of a rectangle is the total space within its boundaries. The formula to calculate the area is:
\[ \text{Area} = l \times w \]
For example, if a rectangle has a length of 8 meters and a width of 5 meters, its area would be:
\[ \text{Area} = 8 \times 5 = 40 \, \text{square meters} \]
- Calculate the Perimeter:
The perimeter is the total distance around the rectangle. To find the perimeter, use the formula:
\[ \text{Perimeter} = 2(l + w) \]
Using the same dimensions, the perimeter would be:
\[ \text{Perimeter} = 2(8 + 5) = 2 \times 13 = 26 \, \text{meters} \]
Example Problem
Consider a rectangular garden with a length of 10 meters and a width of 4 meters. Let's calculate its area and perimeter.
- Area:
\[ \text{Area} = 10 \times 4 = 40 \, \text{square meters} \]
This tells us that the garden covers 40 square meters of space.
- Perimeter:
\[ \text{Perimeter} = 2(10 + 4) = 2 \times 14 = 28 \, \text{meters} \]
The perimeter indicates that you would need 28 meters of fencing to enclose the garden.
Practical Applications
Knowing how to calculate the area and perimeter of rectangles is useful in various practical situations:
- Construction: Estimating the amount of material needed for flooring or wall surfaces.
- Gardening: Determining the size of a garden plot or the amount of fencing required.
- Interior Design: Planning the layout of furniture or designing room spaces.
By following these steps and understanding the formulas, you can confidently tackle any problem involving the area and perimeter of rectangles.
Solving Problems Involving Squares
Squares are special types of rectangles where all four sides are equal in length. Solving problems involving squares is straightforward if you understand the basic properties and formulas related to their area and perimeter. This section will guide you through various problems and provide step-by-step solutions.
Key Formulas for Squares
- Area of a Square:
The area of a square is calculated by squaring the length of one of its sides. The formula is:
\[ \text{Area} = s^2 \]
where \( s \) is the side length of the square.
- Perimeter of a Square:
The perimeter of a square is the total length around the shape, calculated by multiplying the side length by four. The formula is:
\[ \text{Perimeter} = 4s \]
Step-by-Step Problem Solving
- Determine the Side Length:
Identify the side length (\( s \)) of the square. This value is often provided in the problem or can be measured directly.
- Calculate the Area:
Use the side length to find the area using the formula:
\[ \text{Area} = s^2 \]
For example, if a square has a side length of 6 meters, its area is:
\[ \text{Area} = 6^2 = 36 \, \text{square meters} \]
- Calculate the Perimeter:
Determine the perimeter by applying the formula:
\[ \text{Perimeter} = 4s \]
Using the same side length of 6 meters, the perimeter is:
\[ \text{Perimeter} = 4 \times 6 = 24 \, \text{meters} \]
Example Problems
Let’s explore some practical examples to solidify your understanding.
- Example 1: A garden is designed in the shape of a square with each side measuring 8 meters. Calculate the area and the amount of fencing needed to enclose the garden.
- Area:
- Perimeter:
- Example 2: A square tile has an area of 49 square centimeters. Determine the length of each side and the perimeter of the tile.
- Side Length:
- Perimeter:
Solution:
\[ \text{Area} = 8^2 = 64 \, \text{square meters} \]
\[ \text{Perimeter} = 4 \times 8 = 32 \, \text{meters} \]
Solution:
Since the area (\( A \)) is given, find the side length (\( s \)) by taking the square root:
\[ s = \sqrt{A} = \sqrt{49} = 7 \, \text{centimeters} \]
\[ \text{Perimeter} = 4 \times 7 = 28 \, \text{centimeters} \]
Practical Applications
Knowing how to solve problems involving squares is beneficial in many practical scenarios:
- Architecture and Construction: Calculating the area of square rooms or plots of land.
- Interior Design: Planning the layout of square tiles on floors and walls.
- Gardening: Designing square flower beds or garden plots.
By following these steps and applying the formulas, you can efficiently solve any problem involving squares.

Understanding Circle Area and Circumference
A circle is a two-dimensional shape defined as the set of all points in a plane that are equidistant from a fixed point called the center. Understanding the area and circumference of a circle is crucial for solving various geometric problems.
Basic Definitions
- Radius (r): The distance from the center of the circle to any point on its boundary.
- Diameter (d): The distance across the circle through its center, which is twice the radius (d = 2r).
- Circumference (C): The total distance around the circle.
- Area (A): The space enclosed within the boundary of the circle.
Formulas
The formulas for the circumference and area of a circle are derived using the constant π (pi), approximately equal to 3.14159.
- Circumference: \( C = 2\pi r \)
- Area: \( A = \pi r^2 \)
Step-by-Step Calculation
Let's go through the steps to calculate the area and circumference of a circle.
Example Problem
Given a circle with a radius of 5 units:
- Calculate the Circumference:
- Calculate the Area:
Using the formula \( C = 2\pi r \):
\[
C = 2 \times \pi \times 5 \approx 2 \times 3.14159 \times 5 \approx 31.4159 \text{ units}
\]
Using the formula \( A = \pi r^2 \):
\[
A = \pi \times 5^2 \approx 3.14159 \times 25 \approx 78.53975 \text{ square units}
\]
Common Applications
- Determining the material needed to create a circular garden.
- Calculating the length of the fence required to enclose a circular area.
- Finding the space available within circular objects like wheels, plates, and rings.
Practice Problems
- Find the circumference and area of a circle with a radius of 10 units.
- A circular pool has a diameter of 15 meters. Calculate its circumference and area.
- Determine the area of a circle with a circumference of 50 units.
Understanding these fundamental concepts of circle geometry will help in solving more complex problems involving circular shapes.
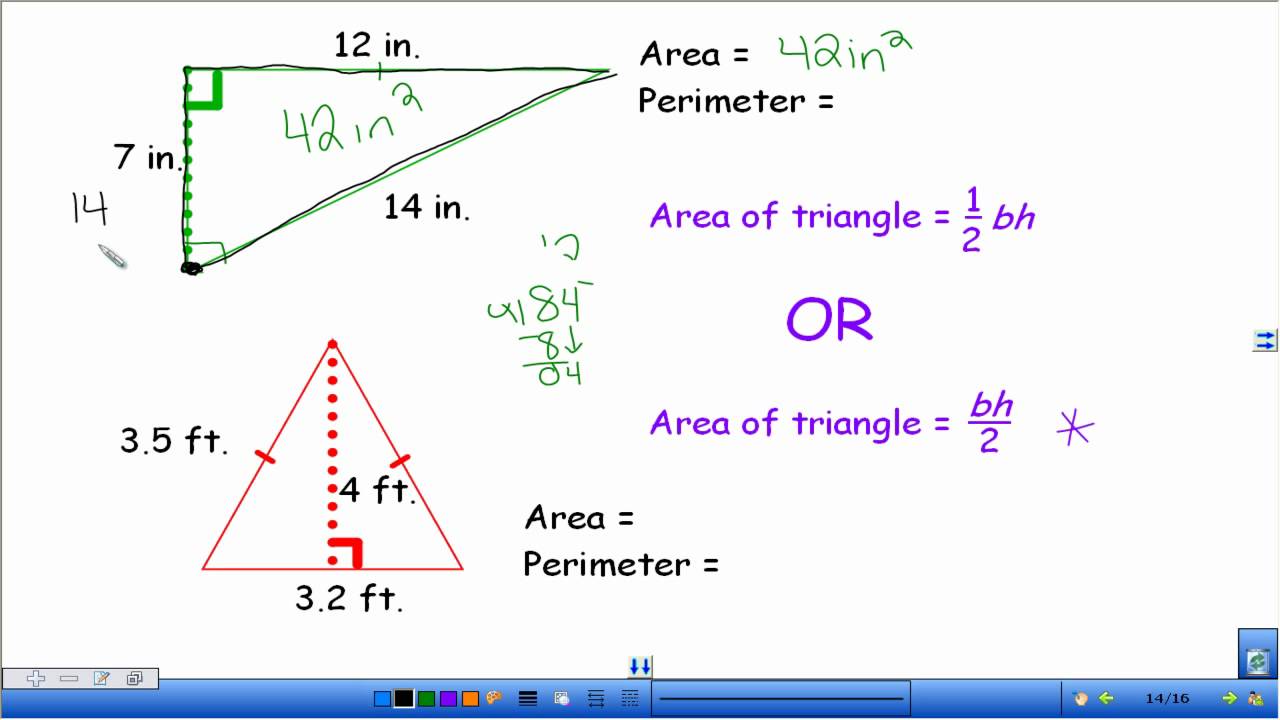
Triangles: Area and Perimeter Calculations
Understanding the area and perimeter of triangles is essential for solving various geometric problems. This section will cover the fundamental formulas and step-by-step methods to calculate the area and perimeter of different types of triangles, including equilateral, isosceles, and scalene triangles.
Area of a Triangle
The area of a triangle can be calculated using the following basic formula:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}
\]
Here, the base is any side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex.
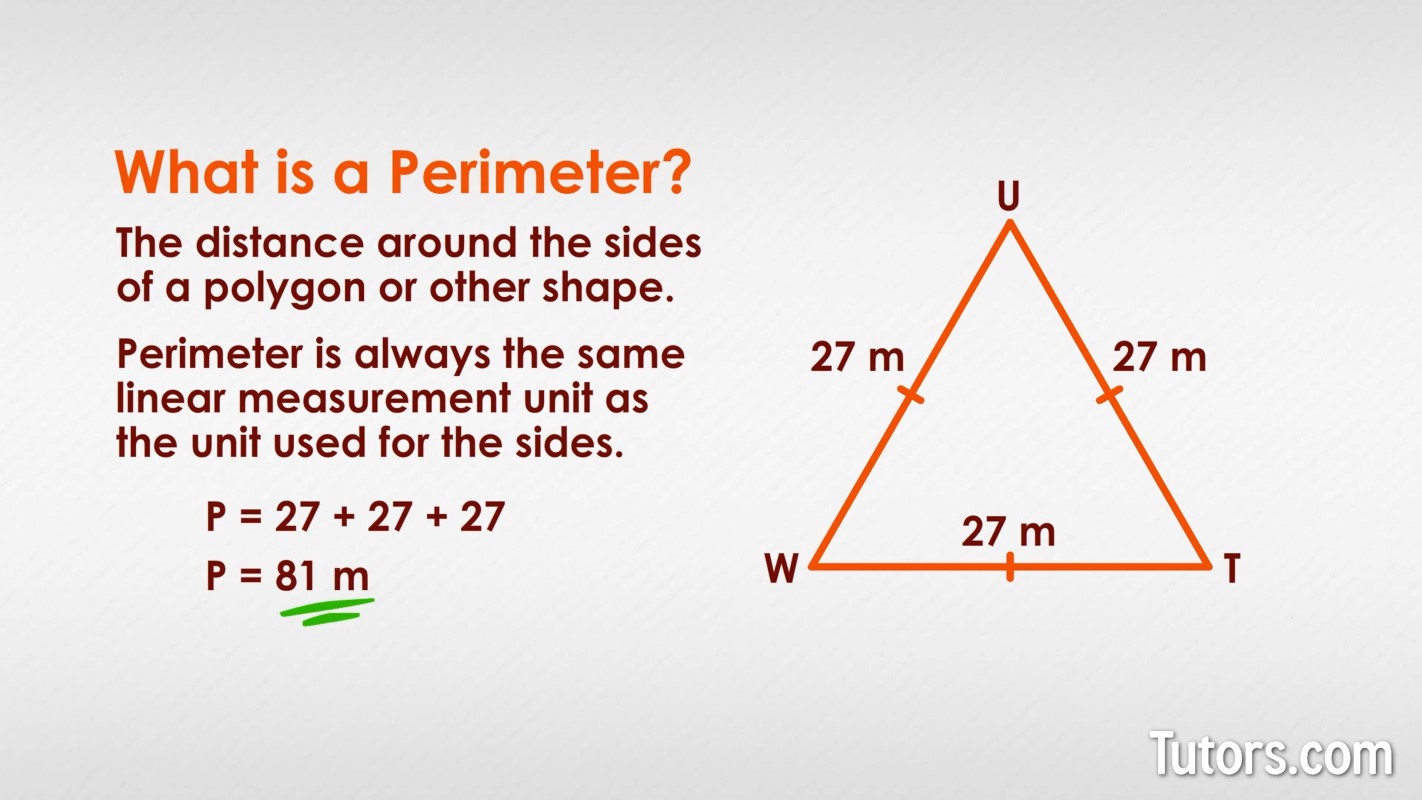
Perimeter of a Triangle
The perimeter of a triangle is the sum of the lengths of its three sides:
\[
\text{Perimeter} = a + b + c
\]
where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
Types of Triangles and Their Calculations
- Equilateral Triangle: All three sides are equal.
\[
\text{Perimeter} = 3a
\]\[
\text{Area} = \frac{\sqrt{3}}{4} a^2
\] - Isosceles Triangle: Two sides are equal.
\[
\text{Perimeter} = 2a + b
\]\[
\text{Area} = \frac{b}{4} \sqrt{4a^2 - b^2}
\] - Scalene Triangle: All sides have different lengths.
\[
\text{Perimeter} = a + b + c
\]To find the area, use Heron's formula:
\[
s = \frac{a + b + c}{2}
\]\[
\text{Area} = \sqrt{s(s - a)(s - b)(s - c)}
\]
Examples
Let's look at a few examples to understand how these formulas are applied:
- Equilateral Triangle:
Given side length \(a = 6\) units, the perimeter is:
\[
\text{Perimeter} = 3 \times 6 = 18 \text{ units}
\]The area is:
\[
\text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = 9\sqrt{3} \text{ units}^2
\] - Isosceles Triangle:
Given \(a = 5\) units and base \(b = 8\) units, the perimeter is:
\[
\text{Perimeter} = 2 \times 5 + 8 = 18 \text{ units}
\]The area is:
\[
\text{Area} = \frac{8}{4} \sqrt{4 \times 5^2 - 8^2} = 12 \text{ units}^2
\] - Scalene Triangle:
Given sides \(a = 7\) units, \(b = 8\) units, and \(c = 5\) units, the perimeter is:
\[
\text{Perimeter} = 7 + 8 + 5 = 20 \text{ units}
\]The semi-perimeter is:
\[
s = \frac{7 + 8 + 5}{2} = 10 \text{ units}
\]The area is:
\[
\text{Area} = \sqrt{10(10 - 7)(10 - 8)(10 - 5)} = \sqrt{10 \times 3 \times 2 \times 5} = 14.14 \text{ units}^2
\]
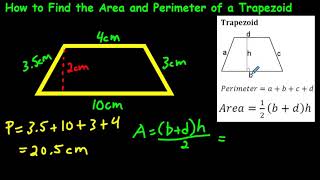
Composite Shapes: Combining Areas and Perimeters
Composite shapes, also known as compound shapes, are shapes that consist of two or more simple geometric shapes. To find the area and perimeter of composite shapes, follow these steps:
Steps to Calculate the Area of Composite Shapes
- Identify the Simple Shapes: Break down the composite shape into simpler shapes such as rectangles, triangles, circles, etc.
- Calculate the Area of Each Simple Shape: Use the appropriate formulas to find the area of each individual shape.
- For rectangles: \( \text{Area} = \text{length} \times \text{width} \)
- For triangles: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- For circles: \( \text{Area} = \pi \times r^2 \)
- Add the Areas Together: Sum the areas of the individual shapes to get the total area of the composite shape.
Steps to Calculate the Perimeter of Composite Shapes
- Identify All the Outer Sides: Determine the lengths of all the outer sides of the composite shape.
- Add the Side Lengths: Sum the lengths of all the outer sides to find the perimeter.
- Ensure that you account for every side only once.
Example 1: Composite Shape with Rectangles
Consider a composite shape consisting of two rectangles:
- Rectangle A: length = 14m, width = 2m
- Rectangle B: length = 8m, width = 5m
Step-by-step area calculation:
- Area of Rectangle A: \( 14 \times 2 = 28 \, \text{m}^2 \)
- Area of Rectangle B: \( 8 \times 5 = 40 \, \text{m}^2 \)
- Total Area: \( 28 + 40 = 68 \, \text{m}^2 \)
Step-by-step perimeter calculation:
- Identify and sum the outer sides:
- Total Perimeter: \( 14 + 2 + 8 + 5 + \text{(other outer sides)} \)
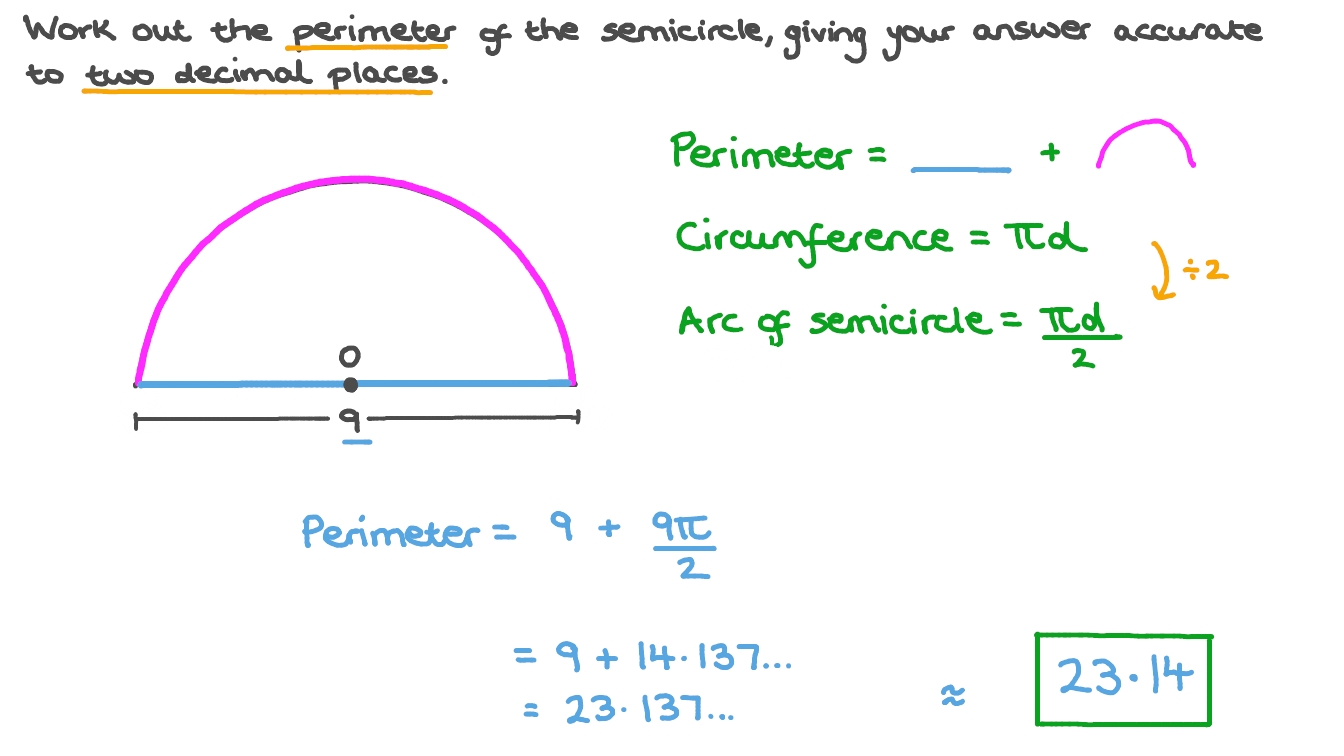
Example 2: Composite Shape with Non-Rectangular Shapes
Consider a composite shape made up of a rectangle and a semicircle:
- Rectangle: length = 10m, width = 6m
- Semicircle with radius = 3m
Step-by-step area calculation:
- Area of Rectangle: \( 10 \times 6 = 60 \, \text{m}^2 \)
- Area of Semicircle: \( \frac{1}{2} \times \pi \times 3^2 = \frac{1}{2} \times \pi \times 9 \approx 14.14 \, \text{m}^2 \)
- Total Area: \( 60 + 14.14 \approx 74.14 \, \text{m}^2 \)
Step-by-step perimeter calculation:
- Perimeter of Rectangle: \( 2 \times (10 + 6) = 32 \, \text{m} \)
- Perimeter of Semicircle: \( \pi \times 3 + 6 \approx 15.42 + 6 = 21.42 \, \text{m} \)
- Total Perimeter: \( 32 + 21.42 = 53.42 \, \text{m} \)
Tips for Success
- Always double-check the measurements and ensure all parts of the composite shape are accounted for.
- Label each part of the composite shape to avoid confusion during calculations.
- Use accurate values for constants like \( \pi \) to ensure precision.
By following these steps and examples, you can effectively find the area and perimeter of any composite shape, making complex shapes easier to handle.
Advanced Problem-Solving Techniques
Solving complex area and perimeter problems often requires a combination of basic formulas, strategic thinking, and advanced mathematical techniques. Here are some advanced techniques to tackle challenging problems:
1. Decomposition and Recomposition
Break down complex shapes into simpler components whose area and perimeter you can easily calculate. Then, sum up the areas and perimeters of these components.
- Example: To find the area of an L-shaped figure, decompose it into two rectangles, calculate their areas separately, and add them together.
2. Use of Algebraic Expressions
Incorporate algebra to form equations that represent the relationships between different parts of a shape. This technique is especially useful in problems involving unknown dimensions.
- Example: If a rectangle's length is twice its width, and you know the perimeter, you can set up an equation to solve for both dimensions.
3. Application of Geometric Properties
Use properties of shapes such as symmetry, similarity, and the Pythagorean theorem to simplify calculations.
- Example: For an isosceles triangle, knowing the properties of equal sides and angles helps in determining area and perimeter efficiently.
4. Optimization Problems
Often, problems may require you to maximize or minimize the area or perimeter given certain constraints. Techniques from calculus, such as finding the derivative and solving for critical points, can be applied here.
- Example: To maximize the area enclosed by a fixed perimeter, use the derivative to find the dimensions that provide the largest area.
5. Coordinate Geometry
Use coordinate geometry to place shapes on a graph and apply formulas to find lengths, areas, and distances between points.
- Example: Calculating the area of a polygon by plotting its vertices on a coordinate plane and using the shoelace formula.
6. Working with Composite Shapes
For shapes that are combinations of multiple basic shapes, calculate each part individually and then combine the results.
- Example: For a composite figure made of a rectangle and a semicircle, calculate the area and perimeter of each part separately before adding them together.
7. Utilizing Software Tools
Advanced geometry software and tools can help visualize complex shapes and verify manual calculations.
- Example: Use tools like GeoGebra to create dynamic models of shapes and explore their properties interactively.
8. Practice with Challenging Problems
Engage with problems that push your understanding and application of these techniques. Websites like NRICH and Khan Academy offer a plethora of challenging problems to practice.
- Example: Solve problems that involve optimizing shapes, working with irregular polygons, or dealing with multiple constraints simultaneously.
By combining these techniques, you can tackle a wide range of advanced area and perimeter problems with confidence.

Word Problems Involving Area and Perimeter
Word problems involving area and perimeter can often be more complex than simple calculations because they require translating a real-world situation into a mathematical model. Below are some detailed steps and examples to help you tackle these problems effectively.
Steps to Solve Word Problems
- Read the Problem Carefully: Understand what is being asked. Identify the shapes involved and the measurements provided.
- Draw a Diagram: Visualizing the problem can help you see the relationships between different elements.
- Write Down Known Values: List the given measurements and what needs to be found.
- Apply Relevant Formulas: Use the appropriate formulas for area and perimeter of the shapes involved.
- Solve Step-by-Step: Break down the problem into smaller parts and solve each part systematically.
- Check Your Work: Review your solution to ensure all parts of the problem have been addressed and the calculations are correct.
Example Problems
Below are a few example problems with solutions:
Example 1: Finding the Perimeter
A rectangular garden is 8 meters long and 5 meters wide. How much fencing is needed to enclose the garden?
- Identify the shape: Rectangle
- Write down known values: Length \( l = 8 \) meters, Width \( w = 5 \) meters
- Apply the perimeter formula for a rectangle: \( P = 2l + 2w \)
- Substitute the values: \( P = 2(8) + 2(5) = 16 + 10 = 26 \) meters
- The perimeter is 26 meters.
Example 2: Finding the Area
A rectangular patio is 12 meters long and 7 meters wide. What is the area of the patio?
- Identify the shape: Rectangle
- Write down known values: Length \( l = 12 \) meters, Width \( w = 7 \) meters
- Apply the area formula for a rectangle: \( A = l \times w \)
- Substitute the values: \( A = 12 \times 7 = 84 \) square meters
- The area is 84 square meters.
Example 3: Combined Shapes
A garden consists of a rectangular section 10 meters by 6 meters and a semicircular section with a diameter of 6 meters. Find the total area of the garden.
- Calculate the area of the rectangle: \( A_{rect} = 10 \times 6 = 60 \) square meters
- Calculate the radius of the semicircle: \( r = \frac{6}{2} = 3 \) meters
- Calculate the area of the semicircle: \( A_{semi} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (3^2) = \frac{1}{2} \pi \times 9 = 4.5 \pi \) square meters
- Approximate the area of the semicircle: \( 4.5 \pi \approx 4.5 \times 3.14 = 14.13 \) square meters
- Add the areas: \( A_{total} = 60 + 14.13 = 74.13 \) square meters
- The total area is approximately 74.13 square meters.
Practice Problems
- A rectangular field is 20 meters long and 15 meters wide. How much area does it cover?
- A swimming pool is in the shape of a circle with a radius of 5 meters. What is the perimeter of the pool?
- A composite shape consists of a rectangle 8 meters by 4 meters and a triangle with a base of 8 meters and a height of 3 meters. Find the total area of the shape.
By following these steps and practicing with a variety of problems, you can become proficient at solving word problems involving area and perimeter.
Real-World Applications of Area and Perimeter
The concepts of area and perimeter are not just confined to the classroom; they have numerous practical applications in everyday life. Understanding these concepts can help in various fields, such as construction, landscaping, interior design, and more.
1. Construction and Architecture
In construction, knowing the area and perimeter is crucial for determining the amount of materials needed. For instance, when building a house, calculating the area of floors and walls helps determine the quantity of tiles, paint, or wallpaper required.
- Example: To calculate the paint needed for a room, you first find the perimeter of the walls and then multiply by the height to get the total area.
2. Landscaping and Gardening
Gardeners and landscapers use area and perimeter to plan layouts for gardens and determine the amount of fencing or paving materials required.
- Example: If you have a rectangular garden that is 20 feet long and 15 feet wide, you can calculate the perimeter to know how much fencing you need: \( P = 2 \times (20 + 15) = 70 \) feet.
3. Interior Design
Interior designers use these measurements to plan furniture placement and ensure everything fits properly within a room. They also calculate the area of floors to determine the amount of flooring material needed.
- Example: To find the carpet required for a room, multiply the length by the width. For a room measuring 12 feet by 10 feet, the area is \( A = 12 \times 10 = 120 \) square feet.
4. Urban Planning
Urban planners use area and perimeter calculations when designing parks, streets, and public spaces. These measurements help in efficiently using space and resources.
- Example: Calculating the area of a park to determine the amount of grass seed or the number of trees that can be planted.
5. Sports Fields
Area and perimeter are used to design and maintain sports fields, ensuring they meet regulation sizes and determining the materials needed for maintenance.
- Example: For a rectangular soccer field that is 100 meters long and 60 meters wide, the perimeter is \( P = 2 \times (100 + 60) = 320 \) meters, and the area is \( A = 100 \times 60 = 6000 \) square meters.
6. Real Estate
Real estate agents and homebuyers use these measurements to evaluate property sizes and compare them. The area helps determine the value of a property, while the perimeter can help in planning modifications like fencing.
- Example: When buying a piece of land, knowing the perimeter helps plan fencing costs, while the area helps understand the usable space.
7. Crafting and DIY Projects
Craft enthusiasts use area and perimeter to measure fabric for sewing projects, wood for carpentry, and other materials for various DIY projects.
- Example: If making a rectangular tablecloth, calculate the area of the table to determine the amount of fabric needed.
8. Everyday Measurements
In daily life, understanding these concepts helps in tasks like wrapping gifts, laying out a picnic blanket, or planning a room layout.
- Example: To wrap a gift, measure the perimeter of the box to know how much wrapping paper you need.
Conclusion
Understanding the practical applications of area and perimeter enhances problem-solving skills and helps in making informed decisions in various real-world scenarios.
Tips for Solving Complex Area and Perimeter Problems
Solving complex area and perimeter problems can be challenging. Here are some tips to help you tackle these problems effectively:
-
Understand the Problem:
Carefully read the problem to identify what is being asked. Determine if you need to find the area, perimeter, or both.
-
Break Down Complex Shapes:
If the shape is complex, break it down into simpler shapes (rectangles, triangles, circles, etc.) for which you know the formulas.
- For example, divide a composite shape into known shapes and calculate their areas separately.
- Use the sum of the areas of these simpler shapes to find the total area.
-
Use the Right Formulas:
Make sure you are using the correct formulas for each shape.
- Rectangle: \( \text{Area} = l \times w \), \( \text{Perimeter} = 2(l + w) \)
- Triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \), \( \text{Perimeter} = a + b + c \)
- Circle: \( \text{Area} = \pi r^2 \), \( \text{Circumference} = 2\pi r \)
-
Label and Organize:
Label all known dimensions and organize your work. Clearly show each step to avoid confusion.
-
Check Units:
Ensure that all measurements are in the same units before performing any calculations.
-
Apply Geometric Properties:
Use geometric properties and theorems (such as the Pythagorean theorem) to find missing dimensions.
-
Verify Your Solution:
Double-check your calculations and make sure your answer makes sense in the context of the problem.
-
Practice Regularly:
Regular practice with a variety of problems will improve your problem-solving skills and help you become more familiar with different types of complex area and perimeter problems.
By following these tips, you can approach complex area and perimeter problems with confidence and accuracy.
Common Mistakes and How to Avoid Them
When solving problems involving area and perimeter, students often encounter common mistakes that can lead to incorrect answers. Recognizing these mistakes and understanding how to avoid them is crucial for mastering these concepts.
-
Confusing Area with Perimeter:
This is a frequent error where students mix up the concepts of area and perimeter. The area measures the space inside a shape, while the perimeter measures the distance around the shape.
Solution: Always start by identifying what the problem is asking for. Draw a diagram and label the sides to visualize the shape better.
-
Incorrect Unit Usage:
Using incorrect units or not converting them properly can lead to mistakes.
Solution: Ensure that all measurements are in the same unit before performing calculations. Convert units if necessary.
-
Forgetting to Include All Sides in Perimeter Calculations:
Sometimes students may overlook a side or use incorrect side lengths when calculating perimeter.
Solution: Double-check that all sides have been included in the calculation. For irregular shapes, break them down into simpler shapes and sum the perimeters.
-
Misunderstanding Formula Applications:
Students might apply the wrong formula or incorrectly apply the right one.
Solution: Memorize key formulas and practice using them in different problems. For example, the area of a rectangle is \( A = l \times w \), and the perimeter is \( P = 2l + 2w \).
-
Errors in Algebraic Manipulations:
When problems involve algebra, mistakes in solving equations can lead to incorrect results.
Solution: Practice solving algebraic equations and check your work by substituting your solution back into the original equation.
By being aware of these common mistakes and taking steps to avoid them, students can improve their accuracy and confidence in solving area and perimeter problems.
Interactive Tools and Practice Problems
Interactive tools and practice problems are essential for mastering the concepts of area and perimeter. These resources offer engaging ways to learn and apply mathematical principles. Below are some highly recommended interactive tools and practice problem sets:
-
Math Playground - Area Blocks
is a game where students can create shapes with specified areas and perimeters on a 12x12 grid. This tool enhances problem-solving and spatial reasoning skills.
-
Khan Academy - Practice Exercises
provides various practice exercises and quizzes to reinforce understanding of area and perimeter. Topics include finding perimeters given side lengths, solving for missing side lengths, and comparing areas and perimeters of rectangles.
-
Interactive Maths - Geoboards
are an excellent way to explore area and perimeter through interactive learning. Students can manipulate virtual bands to form shapes and calculate their areas and perimeters.
-
Math Center - Area and Perimeter Activities
offers a variety of interactive activities for third graders to practice calculating the area and perimeter of different shapes. These activities are designed to build a strong foundation in these concepts.
Here is an example of how to use these tools to solve practice problems:
- Access the game on Math Playground.
- Select a challenge to create a shape with a specified area and perimeter.
- Use the grid to design your shape and verify your calculations within the game.
- Visit to practice additional problems and take quizzes to assess your understanding.
Using these interactive tools regularly will help reinforce your learning and make solving area and perimeter problems more intuitive and fun!
Conclusion and Summary
The journey through understanding the area and perimeter of various shapes has equipped us with essential mathematical tools that are applicable in numerous real-world scenarios. From the basic concepts to more advanced applications, mastering these topics not only enhances our problem-solving skills but also provides a solid foundation for further studies in geometry and related fields.
Here's a brief recap of the key points covered in this guide:
- Introduction to Area and Perimeter: We began with the fundamental definitions of area and perimeter, understanding that the perimeter is the total distance around a shape, while the area is the space enclosed within it.
- Basic Formulas: We explored the essential formulas for calculating the area and perimeter of common shapes such as rectangles, squares, triangles, and circles.
- Advanced Techniques: We delved into solving complex problems involving composite shapes and the use of various strategies to simplify calculations.
- Real-World Applications: We discussed how these concepts are utilized in everyday life, from architectural design to crafting and sports field measurements.
- Interactive Tools and Practice Problems: We provided resources and tools for further practice and exploration, ensuring that learners can reinforce their understanding through hands-on activities.
To summarize:
- The perimeter of a shape is calculated by adding the lengths of all its sides.
- The area is found using specific formulas depending on the shape, such as \( A = l \times w \) for rectangles and \( A = \pi r^2 \) for circles.
- Understanding both concepts is crucial for practical applications in various fields.
With consistent practice and application of these principles, anyone can become proficient in solving problems related to area and perimeter. Remember to use the interactive tools and resources provided to enhance your learning experience. Mathematics is a skill that improves with practice, so keep challenging yourself with new problems and scenarios.
Thank you for using this comprehensive guide on area and perimeter. We hope it has been informative and beneficial in your mathematical journey.
Diện tích và Chu vi
READ MORE:
Tìm Chu vi và Diện tích của Hình phức hợp | Ví dụ Hình chữ L | Hình học | Toán học với Mr. J