Topic what is the perimeter of the triangle: Discover the intriguing world of triangles with our comprehensive guide on "What is the Perimeter of the Triangle?", a journey through geometry, formulas, and practical applications that bring this fundamental concept to life.
Table of Content
- Basic Concept of Triangle Perimeter
- Perimeter Calculation for Different Triangle Types
- Using Pythagorean Theorem for Right Triangles
- Advanced Concepts: Perimeter with Given Angles and Sides
- YOUTUBE: Finding the Perimeter of a Triangle with Mr. J
- Practical Applications and Real-world Examples
- Common Mistakes and Misconceptions
- Practice Problems and FAQs
Basic Concept of Triangle Perimeter
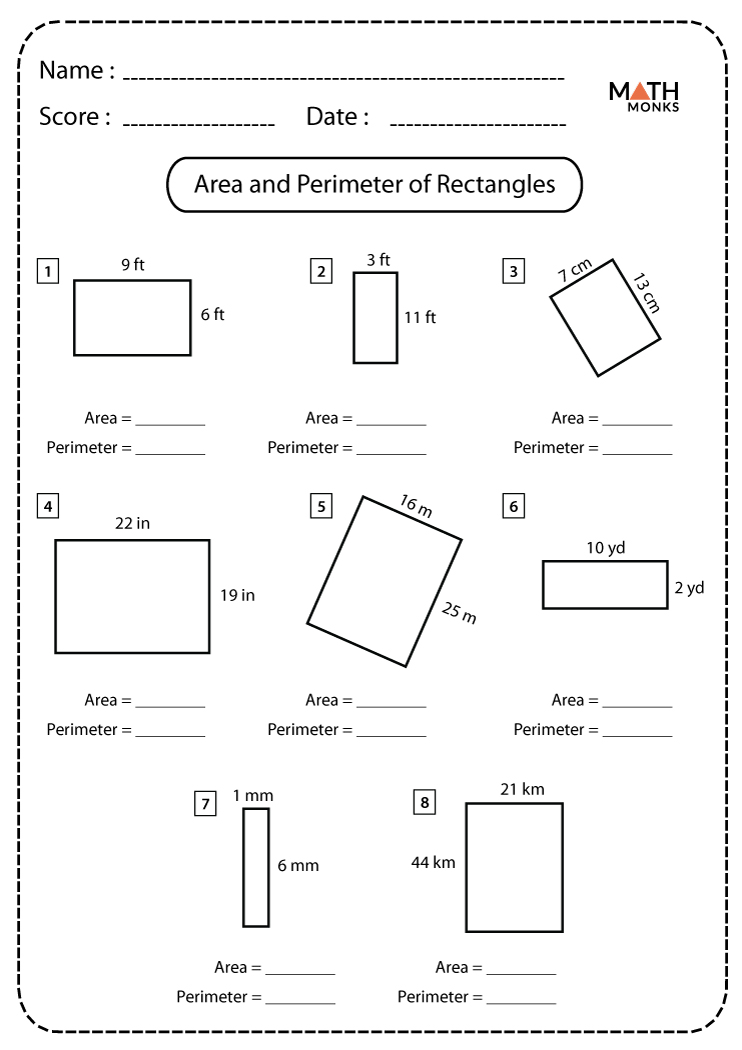
The perimeter of a triangle is the total distance around its boundary, calculated by adding the lengths of its three sides. This fundamental geometric concept applies to various triangles, each with specific properties impacting how their perimeters are determined.
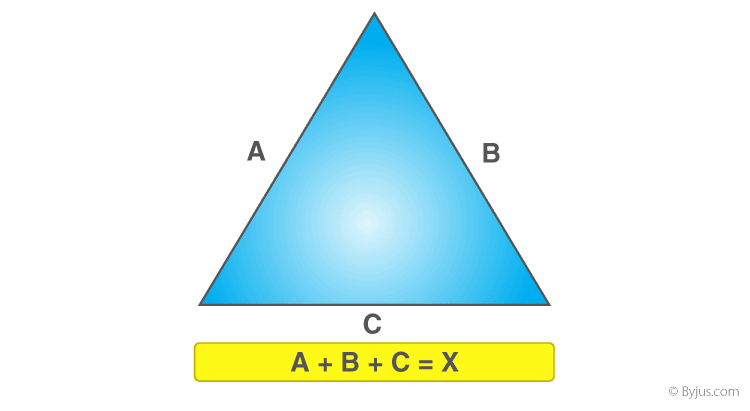
- Standard Triangle: The perimeter is simply the sum of its three sides, denoted as \"a\", \"b\", and \"c\". The formula is P = a + b + c.
- Isosceles Triangle: With two sides of equal length, its perimeter is calculated as P = 2a + b, where \"a\" is the length of the equal sides and \"b\" the base.
- Equilateral Triangle: All sides are equal, making the perimeter calculation straightforward as P = 3a, where \"a\" is the length of one side.
- Right Triangle: If the lengths of two sides are known, the third can be calculated using the Pythagorean Theorem, with the perimeter being the sum of these three sides.
Understanding the concept of triangle perimeter is essential for practical applications in various fields, from architecture to mathematics. This section will explore the nuances of calculating the perimeter for different types of triangles, emphasizing the importance of precision and understanding in geometric calculations.

READ MORE:
Perimeter Calculation for Different Triangle Types
The calculation of a triangle\"s perimeter varies with its type. Here, we explore how to calculate the perimeter for different types of triangles.
- Equilateral Triangle:
- For an equilateral triangle, all sides are of equal length. The formula to calculate the perimeter (P) is simply 3 times the length of one side (a). Hence, P = 3a.
- Isosceles Triangle:
- An isosceles triangle has two sides of equal length (l) and a different base length (b). The perimeter is calculated as P = 2l + b.
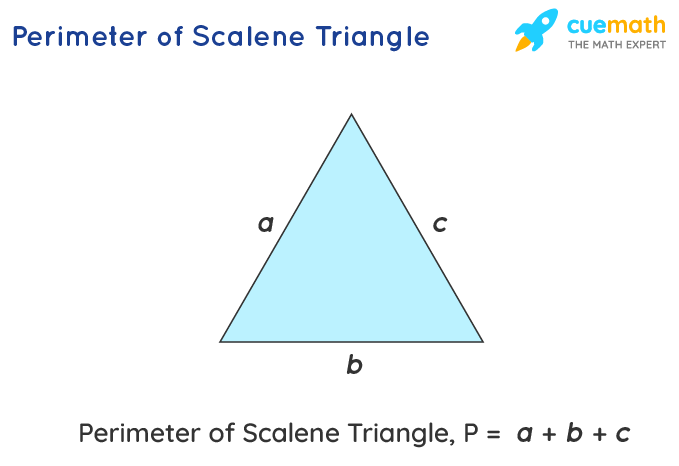
- Scalene Triangle:
- In a scalene triangle, all sides are of different lengths. The perimeter is the sum of all these sides, given as P = a + b + c.
- Right Triangle:
- For a right triangle, if two sides are known, the third side can be calculated using the Pythagorean theorem. The perimeter is then the sum of these three sides.
- Triangle with Given Angles:
- For a triangle with two angles and a side (ASA) or a side and two angles (SAS), the perimeter can be calculated using the law of sines or the law of cosines, respectively.
Understanding these formulas allows for accurate calculations and applications in various real-world scenarios, such as construction and design.
Using Pythagorean Theorem for Right Triangles
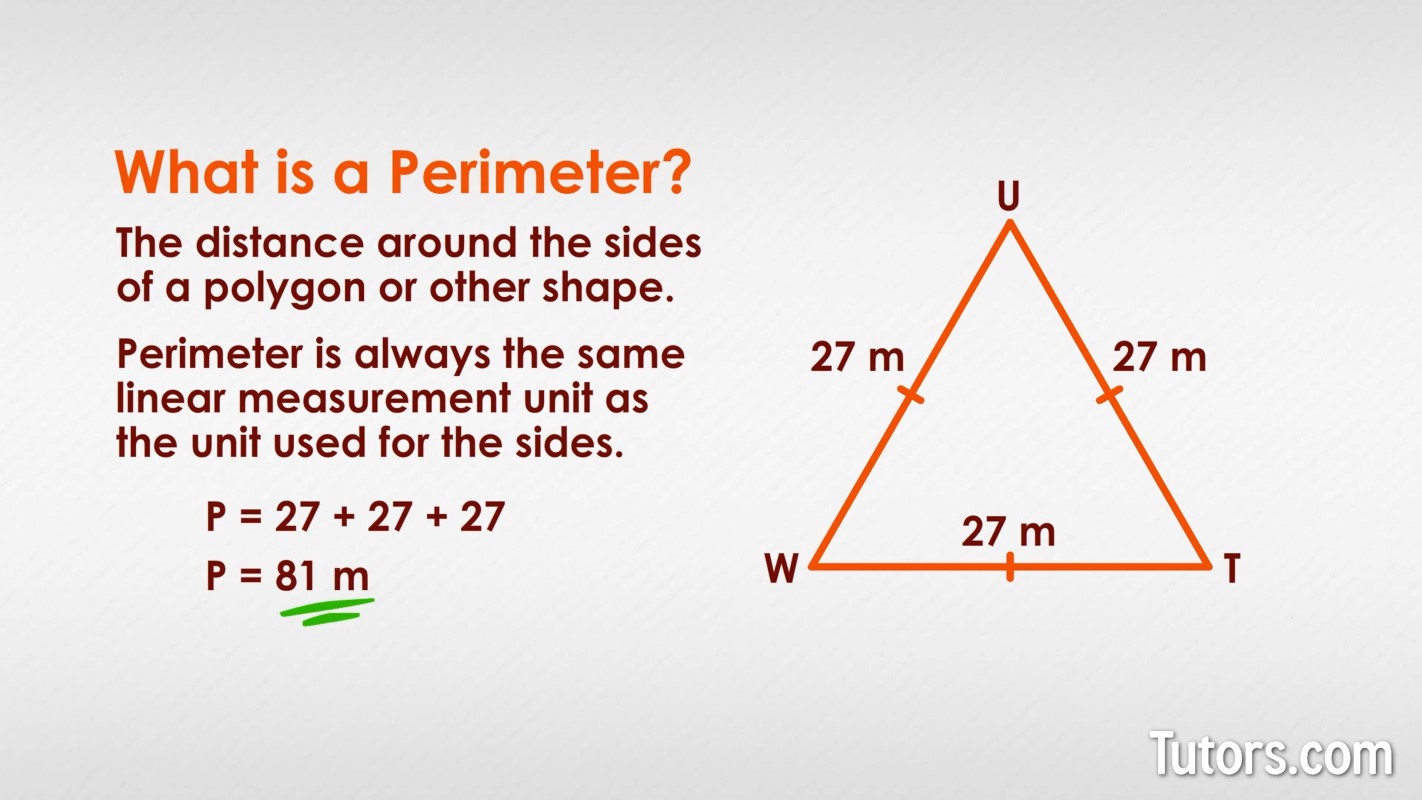
The Pythagorean Theorem is a fundamental principle in geometry, particularly useful in calculating the perimeter of right triangles. A right triangle is characterized by one angle of 90 degrees and two other angles that are acute. The sides forming the right angle are known as the legs, and the side opposite the right angle is the hypotenuse.
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). Mathematically, this is expressed as ( c^2 = a^2 + b^2 ).
- Identifying the Sides: Begin by identifying the two legs (a and b) and the hypotenuse (c) of the right triangle.
- Applying the Theorem: If two sides are known, use the Pythagorean Theorem to find the third side. For example, if the lengths of the legs are known, calculate the hypotenuse using ( c = sqrt{a^2 + b^2} ).
- Calculating the Perimeter: The perimeter (P) of the triangle is the sum of the lengths of its three sides. Once all side lengths are known, calculate the perimeter as ( P = a + b + c ).
Example Problem: Suppose a right triangle has legs of lengths 3 units and 4 units. First, find the length of the hypotenuse using the Pythagorean Theorem: ( c = sqrt{3^2 + 4^2} = sqrt{9 + 16} = sqrt{25} = 5 ) units. The perimeter of the triangle is then ( P = 3 + 4 + 5 = 12 ) units.
Special Considerations
- Only for Right Triangles: The Pythagorean Theorem applies exclusively to right triangles. For other triangle types, different methods are used.
- Accuracy of Measurements: Ensure that the measurements of the sides are accurate. Errors in measurement can lead to incorrect calculations.
- Units Consistency: Maintain consistent units while calculating to avoid errors in the final perimeter value.
Understanding and applying the Pythagorean Theorem is not only crucial in geometry but also serves as a foundation for more advanced mathematical concepts and real-world applications.
Advanced Concepts: Perimeter with Given Angles and Sides
Calculating the perimeter of a triangle when given a combination of sides and angles involves using advanced geometric principles. This process typically employs trigonometric relationships and laws, such as the Law of Sines and the Law of Cosines, to find missing side lengths necessary to determine the perimeter.
Using the Law of Sines
The Law of Sines is useful when the lengths of one side and two angles are known. It states that the ratio of the length of a side to the sine of its opposite angle is constant for all sides and angles in the triangle. Mathematically, it is expressed as ( frac{a}{sin A} = frac{b}{sin B} = frac{c}{sin C} ), where a, b, c are sides and A, B, C are the respective opposite angles.
- Determine the known elements: one side length and two angles.
- Use the Law of Sines to find the remaining sides.
- Sum up all three sides to get the perimeter: ( P = a + b + c ).
Using the Law of Cosines
The Law of Cosines is essential when two sides and the included angle, or three sides, are known. It relates the lengths of the sides of a triangle to the cosine of one of its angles. The formula is ( c^2 = a^2 + b^2 - 2ab cdot cos C ), where C is the angle opposite side c.
- Identify the known sides and angle.
- Apply the Law of Cosines to find the missing side(s).
- Add all three sides to calculate the perimeter: ( P = a + b + c ).
Example Problem Using Law of Sines
Consider a triangle with one side of length 5 units and angles of 30° and 60°. Using the Law of Sines, the other sides can be calculated, and consequently, the perimeter can be determined.
Example Problem Using Law of Cosines
For a triangle with two sides of lengths 7 units and 9 units and an included angle of 45°, use the Law of Cosines to find the third side, and then calculate the perimeter.
- Always ensure angle measurements are accurate to avoid errors in side length calculations.
- Check calculations carefully as trigonometric functions can lead to complex equations.
- Understanding these laws not only aids in solving geometric problems but also enhances spatial reasoning and analytical skills.
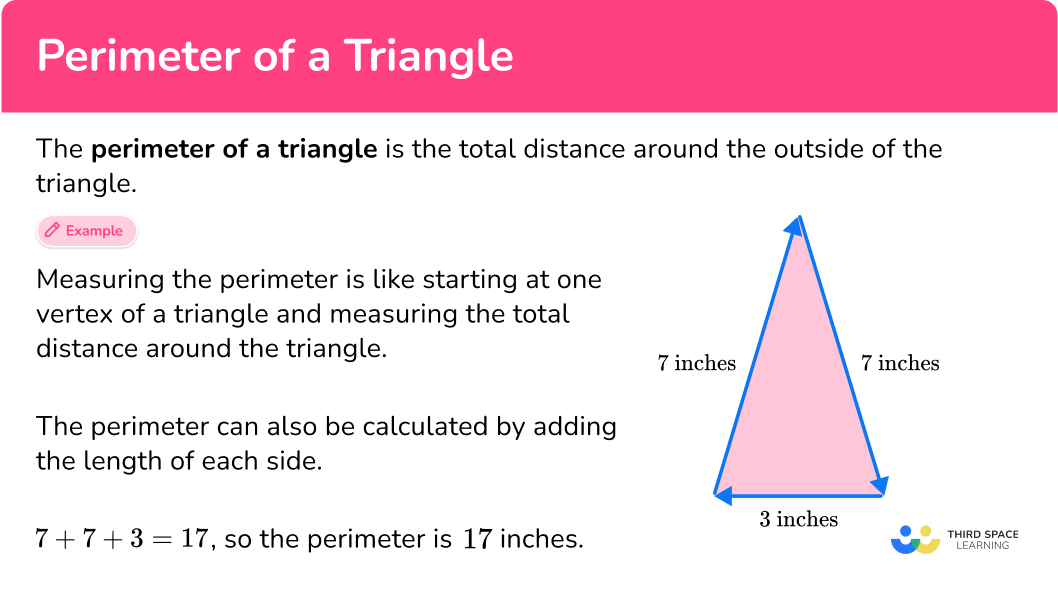
Finding the Perimeter of a Triangle with Mr. J
Discover the secrets of measuring the perimeter in this informative and engaging video! Learn how to calculate the distance around any shape and unlock the key to perfecting your geometry skills.
Finding the Area and Perimeter of a Triangle with Mr. J
Dive into the fascinating world of area measurement with this captivating video. From finding the surface area of a rectangle to exploring the concept of area in real-life scenarios, this video will leave you amazed and eager to learn more.
Practical Applications and Real-world Examples
Understanding the concept of a triangle\"s perimeter has numerous practical applications and real-world examples. The perimeter, which is the sum of all the sides of a triangle, plays a crucial role in various fields such as architecture, engineering, and even everyday life scenarios.
Architecture and Construction
- In architecture, the perimeter of triangular elements is often calculated for designing roofs, bridges, and other structural elements that require geometric precision.
- In construction, understanding the perimeter is essential for material estimation, like fencing around triangular plots or creating triangular garden beds.
Art and Design
- Artists and designers frequently use the concept of perimeter in creating and understanding triangular forms, which are prevalent in modern design and artwork.
- Graphic designers might calculate the perimeter of triangular elements within a layout to maintain visual balance and proportion.
Everyday Applications
- In everyday life, calculating the perimeter can be useful for tasks such as determining the amount of trim needed for a triangular tablecloth or calculating the boundary of a triangular park.
- DIY projects often require measurements of materials, where knowing how to calculate the perimeter of triangular components can be handy.
Education and Problem Solving
- In educational settings, understanding the perimeter of triangles aids in developing problem-solving skills and a deeper understanding of geometry.
- Mathematical problems involving triangles and their perimeters are common in academic competitions and standardized tests, emphasizing practical application skills.
Geographical and Environmental Planning
- Geographers and environmental planners might use the concept of perimeter while mapping triangular land areas or planning land use.
- Understanding the perimeter is also crucial in resource management, such as calculating the fencing required for wildlife reserves with triangular boundaries.
These examples illustrate that the concept of a triangle\"s perimeter is not just a theoretical mathematical concept, but a practical tool used in various real-world applications.
_HOOK_
Common Mistakes and Misconceptions
When learning about the perimeter of triangles, it\"s important to be aware of common mistakes and misconceptions. These errors can lead to incorrect calculations and misunderstandings of geometric principles.
Mistaking Perimeter for Area
- One common error is confusing the perimeter with the area. The perimeter is the sum of all sides of a triangle, whereas the area is the space enclosed within it.
- Remember, perimeter is a linear measure (units), while area is measured in square units (units²).
Incorrect Application of Formulas
- Applying the wrong formulas, such as using the Pythagorean Theorem in non-right triangles, leads to incorrect results.
- Ensure the right formula is applied based on the triangle type (e.g., isosceles, equilateral, or right triangle).
Misunderstanding Triangle Types
- Not recognizing the type of triangle can result in the misuse of formulas or principles. Each type of triangle has its unique properties.
- For instance, in an equilateral triangle, all sides are equal, which simplifies the calculation of the perimeter.
Errors in Measurement
- Incorrectly measuring triangle sides is a frequent source of error. Precision in measurement is crucial.
- When using tools like rulers or protractors, ensure they are properly aligned and read accurately.
Unit Conversion Errors
- Failing to convert units consistently can lead to incorrect perimeter calculations.
- Always check that all measurements are in the same unit before calculating the perimeter.
Calculation Errors
- Simple arithmetic mistakes can result in incorrect perimeters. Double-check calculations for accuracy.
- Using calculators or tools, ensure the correct input of values and operations.
Avoiding these common mistakes and misconceptions can greatly improve accuracy in calculating the perimeter of triangles, leading to a better understanding of geometry.

READ MORE:
Practice Problems and FAQs
Engaging in practice problems is a great way to solidify your understanding of calculating the perimeter of triangles. This section presents a variety of problems to challenge and test your skills, along with frequently asked questions to clarify common doubts.
Practice Problems
- Problem 1: Calculate the perimeter of an equilateral triangle with each side measuring 6 cm.
- Problem 2: Find the perimeter of a right triangle with legs of 3 cm and 4 cm.
- Problem 3: Determine the perimeter of an isosceles triangle with two sides of 5 cm each and a base of 8 cm.
- Problem 4: A scalene triangle has sides measuring 7 cm, 9 cm, and 12 cm. What is its perimeter?
- Problem 5: Using the Law of Sines, find the perimeter of a triangle with one side of 10 cm and opposite angles of 45° and 60°.
Frequently Asked Questions (FAQs)
- Q1: Can the perimeter of a triangle be calculated if only two sides are known?
- A1: No, the perimeter calculation requires the lengths of all three sides. In right triangles, if two sides are known, the third can be calculated using the Pythagorean Theorem.
- Q2: Is the perimeter of an equilateral triangle three times the length of one side?
- A2: Yes, since all sides of an equilateral triangle are equal, the perimeter is three times the length of one side.
- Q3: How is the perimeter of a triangle affected by scaling up or down?
- A3: Scaling a triangle up or down multiplies its perimeter by the same scale factor.
- Q4: Can the perimeter of a triangle be greater than the sum of its two sides?
- A4: Yes, according to the Triangle Inequality Theorem, the sum of any two sides of a triangle must be greater than the length of the third side.
- Q5: How does one calculate the perimeter of a right triangle?
- A5: Add the lengths of the two legs and the hypotenuse. The hypotenuse can be calculated using the Pythagorean Theorem if only the legs are known.
Exploring the world of triangles and their perimeters opens doors to a fascinating journey in geometry, enhancing our understanding of shapes in our daily lives and the wider universe. Dive into this adventure to uncover geometric wonders!