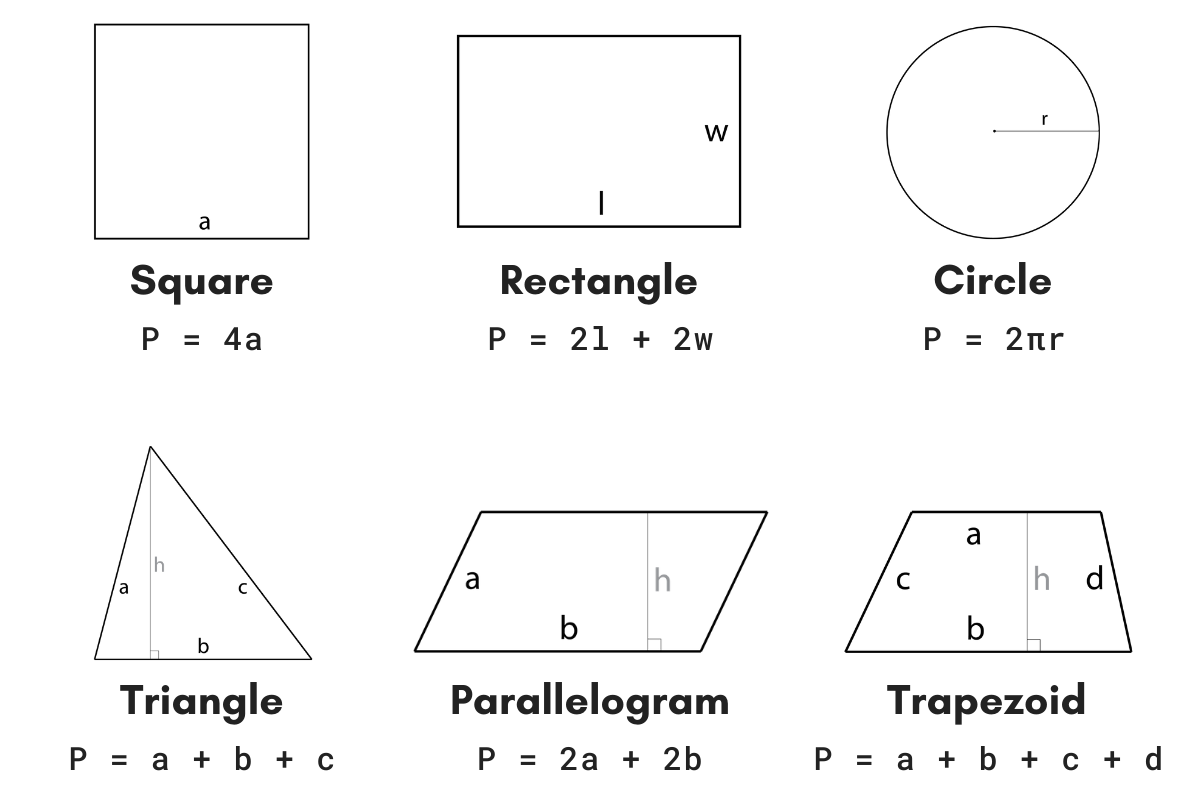
Topic area and perimeter of a triangle formula: Unlock the secrets of triangles with our definitive guide on the "Area and Perimeter of a Triangle Formula," where geometry becomes fascinating and accessible for everyone, from students to math enthusiasts.
Table of Content
- Understanding Triangle Types and Their Properties
- Perimeter of a Triangle: Basic Concept and Formulas
- Detailed Formulas for Perimeter of Different Triangle Types
- Perimeter Calculation Examples for Each Triangle Type
- Area of a Triangle: Introduction and Basic Formula
- YOUTUBE: Finding the Perimeter of a Triangle
- Formulas for Calculating the Area of Different Triangles
- Special Considerations for Right, Equilateral, and Isosceles Triangles
- Area Calculation Examples for Various Triangle Types
- Applying Heron\"s Formula for Triangle Area Calculation
- Advanced Topics: Semi-Perimeter and Its Applications
- Triangle Area and Perimeter: Common FAQs and Their Answers
- Practical Applications: From Classroom to Real Life
Understanding Triangle Types and Their Properties
A triangle, defined by its three sides and three corners, is a fundamental shape in geometry. Its perimeter is the sum of the lengths of these sides. For example, in a triangle with sides of lengths a, b, and c, the perimeter is a + b + c.
- Equilateral Triangle: All sides are equal in length. The perimeter is given as 3a, where \"a\" is the length of each side.
- Isosceles Triangle: Has two equal sides. If a and a are the equal sides and b is the base, its perimeter is 2a + b.
- Scalene Triangle: All sides are of different lengths. Its perimeter is simply the sum of its three sides, a + b + c.
The area of a triangle, which represents the space it encloses, is calculated differently based on available measurements. The most common formula is A = 1/2bh, where \"b\" is the base and \"h\" is the height. Specific formulas are used for different types of triangles:
- Right Triangle: Area is calculated as 1/2 × Base × Height, with one angle being 90°.
- Equilateral Triangle: The area can be found using A = (√3)/4 × side².
- Isosceles Triangle: Area is 1/4b√(4a² - b²), where \"a\" is the length of the equal sides and \"b\" is the base.
- Heron\"s Formula: When the lengths of all three sides are known, Heron’s formula is used: A = √[s(s-a)(s-b)(s-c)], where \"s\" is the semi-perimeter (half of the perimeter) of the triangle.
In addition to these, the law of cosines and the law of sines can be used to find the perimeter when specific side lengths and angles are known. For instance, in a SAS (Side-Angle-Side) triangle, you can calculate the third side using the law of cosines and then find the perimeter. In an ASA (Angle-Side-Angle) triangle, the law of sines helps in determining the remaining sides for the perimeter calculation.

READ MORE:
Perimeter of a Triangle: Basic Concept and Formulas
The perimeter of a triangle is defined as the total length of its three sides. It is a key geometric concept and plays a vital role in various applications. Understanding how to calculate the perimeter of different types of triangles is essential in geometry.
- Basic Formula: The basic formula for the perimeter of a triangle is P = a + b + c, where a, b, and c are the lengths of the triangle\"s sides.
- Equilateral Triangle: For an equilateral triangle, where all sides are of equal length l, the perimeter is given by P = 3l.
- Isosceles Triangle: In an isosceles triangle, with two equal sides of length a and base b, the perimeter is calculated as P = 2a + b.
- Scalene Triangle: A scalene triangle has all sides of different lengths. Here, the perimeter is simply the sum of these lengths.
- Right Triangle: The perimeter of a right triangle, which includes a base (b), perpendicular (p), and hypotenuse (h), is calculated using the Pythagorean theorem: h² = b² + p², followed by P = b + p + h.
It\"s important to always include the correct units in your calculations. For example, if the sides are measured in centimeters, the perimeter should also be expressed in centimeters.
Understanding these formulas allows for solving various practical problems, such as determining the length of a fence needed to enclose a triangular area or calculating the distances involved in a triangular race course.

Detailed Formulas for Perimeter of Different Triangle Types
The perimeter of a triangle is the sum of the lengths of its sides. Different types of triangles have different formulas for calculating their perimeters.
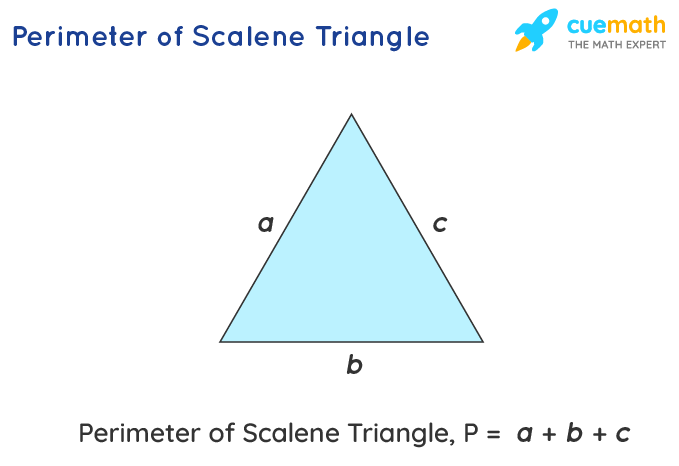
- Perimeter of a Scalene Triangle: For a triangle with sides of different lengths (a, b, and c), the formula is simply the sum of its sides. Perimeter = a + b + c.
- Perimeter of an Equilateral Triangle: In an equilateral triangle, all sides are equal in length. If \"a\" is the length of a side, the perimeter is 3 times the length of a side. Perimeter = 3a.
- Perimeter of an Isosceles Triangle: This triangle has two equal sides. If \"s\" is the length of the equal sides and \"b\" is the base, the perimeter is the sum of the lengths of all sides. Perimeter = 2s + b.
- Perimeter of a Right Triangle: For a right triangle, the perimeter can be found by adding the lengths of the two shorter sides (base and height) and the hypotenuse. If the shorter sides are a and b, and the hypotenuse is c, then Perimeter = a + b + c. The hypotenuse can be found using the Pythagorean theorem (c = √(a² + b²)).
For triangles where certain sides or angles are known, the perimeter can also be calculated using trigonometric formulas like the law of cosines and the law of sines.

Perimeter Calculation Examples for Each Triangle Type
Calculating the perimeter of a triangle involves adding the lengths of its sides. Here are examples for different types of triangles:
- Scalene Triangle:
- For a triangle with sides a, b, and c, the perimeter is the sum of these sides. Example: For a triangle with sides 5 units, 10 units, and 6 units, the perimeter is calculated as 5 + 10 + 6 = 21 units.
- Equilateral Triangle:
- All sides are equal in an equilateral triangle. If each side is \"a\", then the perimeter is 3a. Example: If a side is 8 cm, the perimeter is 3 × 8 = 24 cm.
- Isosceles Triangle:
- In an isosceles triangle, two sides are equal. If \"s\" is the length of the equal sides and \"b\" is the base, the perimeter is 2s + b. Example: For equal sides of 7 inches and base 5 inches, the perimeter is 2 × 7 + 5 = 19 inches.
- Right Triangle:
- A right triangle has one 90-degree angle. Example: For a right triangle with sides 4 inches, 3 inches, and a hypotenuse 5 inches (calculated using the Pythagorean theorem), the perimeter is 4 + 3 + 5 = 12 inches.
These examples illustrate how the perimeter of a triangle varies depending on its type and the lengths of its sides.

Area of a Triangle: Introduction and Basic Formula
The area of a triangle is a measure of the space enclosed within its three sides. It is a fundamental concept in geometry and is used in various fields such as engineering, architecture, and mathematics.
The basic formula for calculating the area of a triangle is given by:
- Area (A) = 1/2 × base (b) × height (h): This formula applies when the base and the perpendicular height of a triangle are known.
Besides the basic formula, other formulas based on different known dimensions of the triangle can be used:
- Heron\"s Formula: Used for scalene triangles where all three sides are known. Area = √[s(s - a)(s - b)(s - c)], where s is the semi-perimeter, and a, b, and c are the sides of the triangle.
- For Right-Angled Triangles: Area = 1/2 × Base × Height, where the base and height are the two sides that form the right angle.
- For Equilateral Triangles: Area = (√3)/4 × side², when the length of a side is known.
- For Isosceles Triangles: Area = 1/4 × b√(4a² - b²), where b is the base, and a is the length of an equal side.
Understanding these formulas allows for accurate calculations of the area of various triangle types, which is essential in both theoretical and practical applications.

_HOOK_
Finding the Perimeter of a Triangle
Perimeter: Discover the fascinating world of perimeter calculations in this video! Explore how to measure and calculate perimeters of different shapes, from basic squares and rectangles to more complex polygons. With clear examples and step-by-step instructions, you\'ll quickly become a pro at finding perimeters. Watch now and unlock the secrets of perimeter calculation!
Finding the Area and Perimeter of a Triangle
Area: Dive into the exciting world of area calculations with this captivating video! Learn how to measure and calculate areas of various shapes, including squares, circles, triangles, and more. From basic formulas to practical real-life applications, this video will empower you with the knowledge and skills to confidently calculate areas. Don\'t miss out on this enlightening experience - press play now and unravel the mysteries of area calculation!
Formulas for Calculating the Area of Different Triangles
Calculating the area of a triangle depends on the type and dimensions of the triangle. Below are formulas for different types of triangles:
- General Triangle (Base and Height Known):
- The area of a triangle can be calculated by the formula ( A = frac{1}{2} imes ext{base} imes ext{height} ). It is applicable when the base and height of the triangle are known.
- Scalene Triangle (All Sides Known - Heron\"s Formula):
- For a scalene triangle, where all three sides are known (a, b, c), the area can be calculated using Heron\"s Formula: ( ext{Area} = sqrt{s(s - a)(s - b)(s - c)} ), where ( s ) is the semi-perimeter ( (s = frac{a + b + c}{2}) ).
- Right-Angled Triangle:
- In a right-angled triangle, the area can be found by ( ext{Area} = frac{1}{2} imes ext{Base} imes ext{Height} ), where the base and height are the two sides forming the right angle.
- Equilateral Triangle (Side Known):
- The area of an equilateral triangle, where all sides are equal (side = a), is given by ( ext{Area} = frac{sqrt{3}}{4} imes a^2 ).
- Isosceles Triangle (Equal Side and Base Known):
- For an isosceles triangle, with an equal side length (a) and base (b), the area is calculated as ( ext{Area} = frac{1}{4} imes b imes sqrt{4a^2 - b^2} ).
These formulas cater to different scenarios and help in accurately calculating the area of various types of triangles.
Special Considerations for Right, Equilateral, and Isosceles Triangles
Calculating the area and perimeter of triangles requires an understanding of their specific properties. Right, equilateral, and isosceles triangles have unique characteristics that influence their formulas.
Right Triangle
In a right triangle, the area is calculated using the formula ( ext{Area} = frac{1}{2} imes ext{base} imes ext{height} ). The base and height are the two sides that form the right angle. The perimeter is the sum of all three sides, calculated as ( ext{Perimeter} = a + b + c ), where ( a ), ( b ), and ( c ) are the lengths of the sides.
Equilateral Triangle
All sides of an equilateral triangle are equal. Its area is found using the formula ( ext{Area} = frac{sqrt{3}}{4} imes a^2 ), where ( a ) is the length of a side. The perimeter is simply ( ext{Perimeter} = 3 imes a ).
Isosceles Triangle
An isosceles triangle has two equal sides. Its area can be calculated using ( ext{Area} = frac{1}{2} imes ext{base} imes ext{height} ). The perimeter is the sum of the lengths of the two equal sides and the base, given by ( ext{Perimeter} = 2 imes s + b ), where ( s ) is the length of the equal sides and ( b ) is the base.
For detailed formulas and examples, refer to the explanations provided by Embibe, Khan Academy, Cuemath, and Byju\"s.

Area Calculation Examples for Various Triangle Types
Understanding the area calculation for different types of triangles is essential in geometry. This section provides examples for calculating the area of various triangles including equilateral, isosceles, and right-angled triangles.
Example 1: Area of a Right-Angled Triangle
Consider a right-angled triangle with a base of 8 cm and a height of 7 cm. The area is calculated using the formula: Area = 1/2 × base × height. So, the area = 1/2 × 8 cm × 7 cm = 28 cm2.
Example 2: Area of an Equilateral Triangle
For an equilateral triangle with each side measuring 2 cm, the area can be calculated using the formula: Area = (√3/4) × side2. Thus, the area = (√3/4) × 2 cm2 ≈ 1.73 cm2.
Example 3: Area of an Isosceles Triangle
An isosceles triangle with a base of 4 cm and equal sides of 3 cm each, the area is calculated as: Area = 1/4 × base × √(4 × side2 - base2). Therefore, the area = 1/4 × 4 cm × √(4×3 cm2 - 4 cm2) ≈ 5.56 cm2.
Example 4: Area of a Triangle using Heron\"s Formula
For a triangle with sides of lengths 4 in, 7 in, and 9 in, the area can be calculated using Heron\"s formula. First, find the semi-perimeter (s): s = (4 + 7 + 9)/2 = 10 inches. The area = √[10(10 - 4)(10 - 7)(10 - 9)] ≈ 13.416 in2.
These examples illustrate how to apply different formulas to calculate the area of triangles. The choice of formula depends on the type of triangle and the dimensions given.
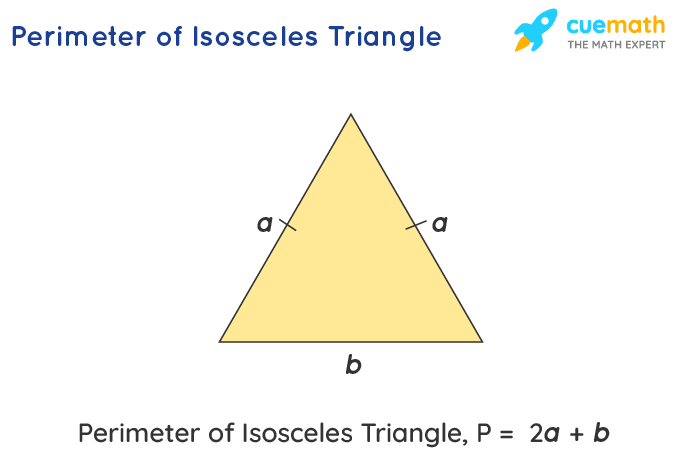
Applying Heron\"s Formula for Triangle Area Calculation
Heron\"s Formula provides a method to calculate the area of a triangle when you know the lengths of all three sides. It is especially useful for triangles that are not right-angled, where traditional methods (like half base times height) may not apply directly.
To use Heron\"s Formula, we first find the semi-perimeter of the triangle, which is half the sum of its sides. Then, we apply the formula to calculate the area.
- Calculate the semi-perimeter (s): ( s = frac{a + b + c}{2} ) where ( a, b, ) and ( c ) are the lengths of the sides of the triangle.
- Calculate the area (A): ( A = sqrt{s imes (s - a) imes (s - b) imes (s - c)} ).
Here is an example to illustrate:
- Consider a triangle with sides of length 3 cm, 4 cm, and 5 cm.
- First, calculate the semi-perimeter: ( s = frac{3 + 4 + 5}{2} = 6 ) cm.
- Then, calculate the area using Heron\"s formula: ( A = sqrt{6 imes (6 - 3) imes (6 - 4) imes (6 - 5)} = sqrt{6 imes 3 imes 2 imes 1} = sqrt{36} ) sq cm.
- The area of the triangle is 6 sq cm.
This method is versatile and can be used for any type of triangle, whether it is equilateral, isosceles, scalene, or right-angled.
Advanced Topics: Semi-Perimeter and Its Applications
The semi-perimeter of a triangle is an important concept in geometry, especially when calculating the area of a triangle using Heron\"s Formula. The semi-perimeter is half the sum of the lengths of the sides of a triangle. It is represented by the symbol (s) and is calculated as (s = frac{a + b + c}{2}), where (a), (b), and (c) are the lengths of the sides of the triangle.
Applications of the semi-perimeter are not limited to just area calculation. It is also used in solving problems related to the triangle\"s geometry, such as finding the radius of the inscribed circle (incircle) or the circumscribed circle (circumcircle).
- Calculating the Area: Using Heron\"s Formula, the area (A) of a triangle can be calculated as (A = sqrt{s(s-a)(s-b)(s-c)}), where (s) is the semi-perimeter.
- Inscribed Circle Radius: The radius (r) of the inscribed circle is given by (r = frac{A}{s}), where (A) is the area of the triangle and (s) is the semi-perimeter.
- Circumscribed Circle Radius: For a triangle with sides (a), (b), and (c), the radius (R) of the circumcircle can be found using the formula (R = frac{abc}{4A}), where (A) is the area of the triangle.
Examples of Semi-Perimeter in Use:
- For a triangle with sides 5 cm, 6 cm, and 7 cm, the semi-perimeter (s) would be (s = frac{5 + 6 + 7}{2} = 9) cm.
- Applying Heron\"s Formula, the area of this triangle can be calculated, and subsequently, the radius of the inscribed or circumcircle can be determined.
_HOOK_
Triangle Area and Perimeter: Common FAQs and Their Answers
- What is the formula for the area of a triangle?
- The area of a triangle can be calculated using the formula (A = frac{1}{2} imes ext{base} imes ext{height}) for right, isosceles, and equilateral triangles. For triangles where all three sides are known, Heron\"s formula can be used: (A = sqrt{s(s-a)(s-b)(s-c)}), where (s) is the semi-perimeter ((s = frac{a + b + c}{2})) and (a), (b), (c) are the sides of the triangle.
- How is the perimeter of different types of triangles calculated?
- For an equilateral triangle (all sides equal): (P = 3 imes a).
- For an isosceles triangle (two sides equal): (P = 2a + b).
- For a scalene triangle (all sides different): (P = a + b + c).
- Can a triangle have the same area and perimeter?
- A triangle can have the same area and perimeter in specific cases, known as equable shapes. However, this is not common and usually occurs under certain geometric conditions.
- What is the perimeter of an isosceles right triangle?
- The perimeter of an isosceles right triangle can be calculated using the formula (P = 2l + sqrt{2}l), where (l) is the length of the two equal legs.
- How to find the area and perimeter of a triangle with given coordinates?
- To find the area and perimeter of a triangle with given coordinates, calculate the lengths of all sides using the distance formula, then apply the relevant formulas for area and perimeter.
READ MORE:
Practical Applications: From Classroom to Real Life
Understanding the area and perimeter of triangles extends beyond the classroom, finding practical applications in various fields of everyday life.
- Architectural Design and Construction: Architects and engineers use triangle area and perimeter calculations for designing structures, including buildings and bridges. These calculations help in determining the amount of materials needed, like tiles for flooring or paint for walls.
- Agricultural Planning: In agriculture, these concepts are crucial for land measurement and planning. They assist in estimating the land area required for different agricultural activities, enabling efficient use of space and resources.
- Geographic Mapping and Navigation: Area and perimeter calculations are vital in geography for mapping and navigation purposes. They help in calculating distances and areas on maps, which is essential for travel and exploration.
- Decoration and Interior Design: In interior design, calculating the area of triangular spaces is key to efficiently using materials like wallpaper or fabric. The perimeter measurement is useful for placing decorative items or furniture along the edges of a room.
- Sports Fields and Recreational Areas: The layout of sports fields often involves triangle calculations to mark out the playing areas accurately and to ensure the fields meet regulatory dimensions.
- Art and Craft: Triangle measurements are used in various art and craft projects for creating geometric designs and ensuring symmetry and balance in the artwork.
The practical applications of triangle area and perimeter calculations demonstrate the importance of these concepts in our daily lives, highlighting the connection between mathematical theories and real-world scenarios.
Embark on a mathematical journey exploring the fascinating world of triangles! Discover how the simple formulas for area and perimeter unlock a universe of practical applications, from architectural designs to geographical mapping. Join us in unraveling these geometric mysteries, making math both fun and applicable in everyday life.