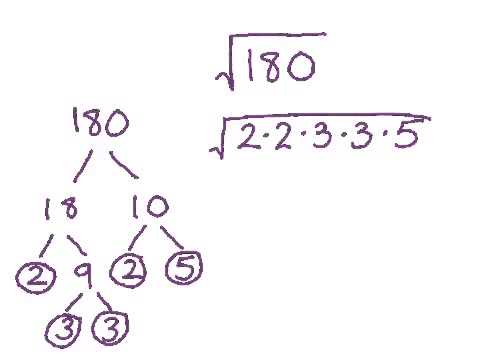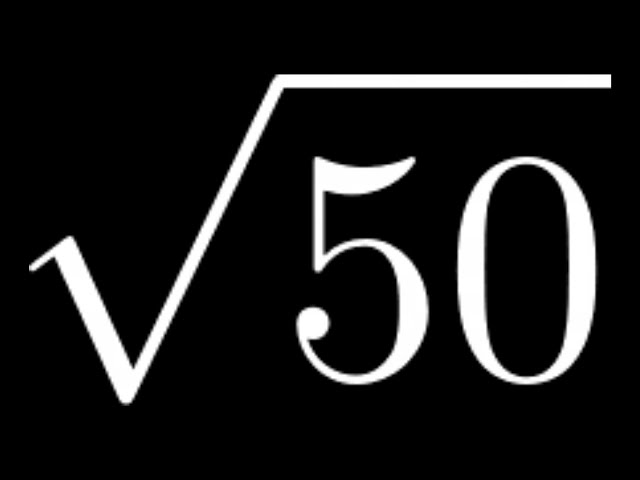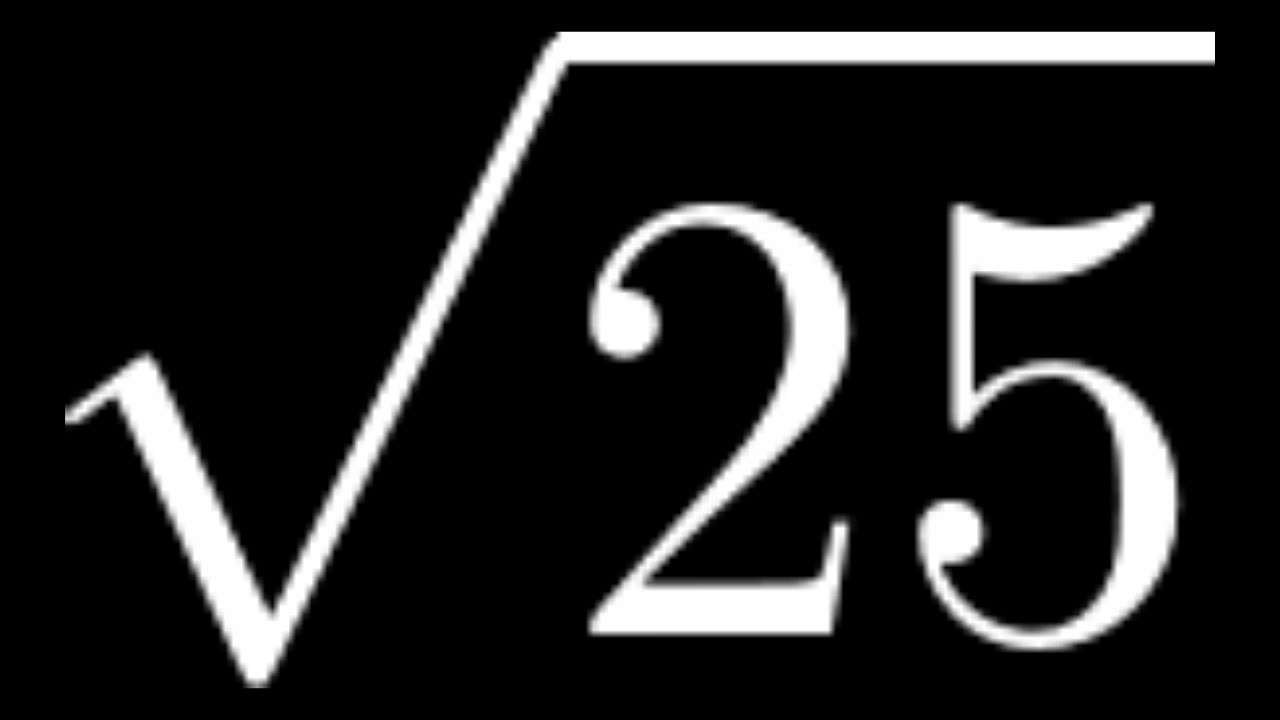Topic square root big numbers: Understanding how to find the square root of big numbers is essential for tackling complex mathematical problems. This article explores various methods and tips to simplify and accurately calculate square roots, helping you enhance your mathematical skills and confidence.
Table of Content
- Understanding Square Roots of Large Numbers
- Introduction
- Methods for Finding Square Roots
- Long Division Method
- Newton-Raphson Method
- Estimation and Approximation
- Mathematical Tables
- Algorithms for Big Numbers
- Examples and Practice Problems
- Applications
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai của các số lớn một cách nhẩm, giúp bạn nhanh chóng và dễ dàng tính toán mà không cần đến máy tính.
Understanding Square Roots of Large Numbers
Finding the square root of large numbers can be challenging but is manageable with the right techniques. Below are methods and examples to help you understand and calculate square roots of big numbers.
Step-by-Step Method for Finding Square Roots
- Identify the unit digit of the number. For example, if the number is 4489, the unit digit is 9. Possible unit digits for the square root are 3 and 7 because \(3^2 = 9\) and \(7^2 = 49\).
- Consider the first part of the number, ignoring the unit digit. For 4489, this is 44, which lies between \(6^2\) and \(7^2\) (since \(6^2 < 44 < 7^2\)).
- Assume the ten’s digit of the square root to be the lower number (6 in this case). Now, consider numbers ending in 63 and 67.
- Multiply 6 (the ten’s digit) by the next integer (7): \(6 \times 7 = 42\). Since 42 is less than 44, the correct number is 67.
- Therefore, \(\sqrt{4489} = 67\).
Example Calculations
Let’s look at another example:
- Number: 7056
- Unit digit is 6, so possible unit digits for the square root are 4 and 6 (\(4^2 = 16\), \(6^2 = 36\)).
- The first part of the number is 70, lying between \(8^2\) and \(9^2\) (since \(8^2 < 70 < 9^2\)).
- Assume the ten’s digit to be 8. Now, consider 84 and 86.
- Multiply 8 by 9: \(8 \times 9 = 72\). Since 72 is greater than 70, the correct number is 84.
- Therefore, \(\sqrt{7056} = 84\).
Simplifying Square Roots
To simplify square roots, find factors that are perfect squares. For example:
- \(\sqrt{27}\): The factors of 27 are 1, 3, 9, 27. Since 9 is a perfect square, \(\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}\).
- \(\sqrt{144}\): Since 144 is a perfect square (\(12^2\)), \(\sqrt{144} = 12\).
Using the Square Root Formula
Remember the fundamental property of square roots: \(\sqrt{x \times y} = \sqrt{x} \times \sqrt{y}\). This property helps in simplifying complex square roots.
Square Root Table
| Number | Square Root |
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
Conclusion
By breaking down the process and using these methods, you can find the square roots of large numbers efficiently. Practice with different numbers to become more comfortable with these techniques.

READ MORE:
Introduction
Finding the square root of large numbers can be a complex but fascinating process.
It involves breaking down the number into smaller components and applying methods
such as prime factorization, long division, or estimation techniques. This section
will explore various strategies to efficiently calculate the square root of big numbers
without relying on calculators, enabling a deeper understanding of mathematical principles.
Methods for Finding Square Roots
- Long Division Method: This method involves manually dividing the number into smaller parts to estimate the square root, iterating until the desired precision is achieved.
- Newton-Raphson Method: An iterative algorithm that starts with an initial guess and refines it using calculus principles, converging quickly to the accurate square root.
- Estimation and Approximation: Techniques like the Babylonian method use successive approximations to refine the square root estimate, particularly useful for mental calculations.
- Using Mathematical Tables: Historical and modern tables list precomputed square roots, aiding in quick lookup and verification of square roots for specific values.
- Algorithms for Big Numbers: Advanced computational algorithms, including binary search and iterative methods tailored for large numbers, provide efficient and precise square root calculations in computer science applications.
Long Division Method
The long division method is a systematic approach for finding the square root of large numbers. This method is particularly useful for manual calculations and is also used in some computer algorithms. Below are the detailed steps to find the square root of a number using the long division method:
- Group the digits of the number into pairs, starting from the decimal point and moving both left and right. For whole numbers, start from the right. Each pair of digits, including single digits, will be processed.
- Find the largest number whose square is less than or equal to the first group or pair. This number is the first digit of the square root. Subtract its square from the first group and bring down the next pair of digits.
- Double the current result (ignoring the remainder) and write it as the divisor's tens part. Find a digit which, when placed at the divisor's unit part and multiplied by the new divisor, gives a product less than or equal to the current dividend. This digit becomes the next digit of the square root.
- Subtract the product from the current dividend and bring down the next pair of digits. Repeat the process until all pairs have been processed.
Below is an example to illustrate the method:
Example: Find the square root of 7056.
- Group the digits: (70)(56).
- The largest number whose square is less than or equal to 70 is 8 (since \(8^2 = 64\)).
- Subtract 64 from 70 to get 6, then bring down the next pair (56) to get 656.
- Double 8 to get 16. Find a digit x such that 16x multiplied by x is less than or equal to 656. The digit is 4 (since \(164 \times 4 = 656\)).
- Subtract 656 from 656 to get 0.
Therefore, the square root of 7056 is 84.
The steps can be summarized in a tabular form:
| Step | Action | Explanation |
| 1 | 70 | Find the largest number whose square is ≤ 70 (8). Subtract 64 from 70 to get 6. |
| 2 | 656 | Bring down the next pair to get 656. Double the quotient (8) to get 16. |
| 3 | 164 | Find x such that 16x * x ≤ 656 (x=4). Subtract 656 from 656 to get 0. |
By following these steps, you can manually calculate the square root of any large number using the long division method.
Newton-Raphson Method
The Newton-Raphson method is an efficient iterative technique for finding the square root of large numbers. It uses the concept of linear approximation to progressively find a more accurate estimate. Here are the detailed steps to apply the Newton-Raphson method:
- Start with an initial guess \( x_0 \). A reasonable initial guess might be \( x_0 = \frac{N}{2} \) or \( x_0 = 1 \) where \( N \) is the number whose square root we are trying to find.
- Use the iterative formula to find a better approximation: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right) \] where \( x_n \) is the current approximation and \( x_{n+1} \) is the next, more accurate approximation.
- Repeat the process until the difference between successive approximations is less than a chosen tolerance level (i.e., \(|x_{n+1} - x_n| < \epsilon \), where \( \epsilon \) is a small positive number).
Below is an example to illustrate the method:
Example: Find the square root of 40401 using the Newton-Raphson method.
- Initial guess: \( x_0 = \frac{40401}{2} = 20200.5 \).
- Apply the iterative formula:
- \( x_1 = \frac{1}{2} \left( 20200.5 + \frac{40401}{20200.5} \right) = 10101.249975 \)
- \( x_2 = \frac{1}{2} \left( 10101.249975 + \frac{40401}{10101.249975} \right) = 5052.624895 \)
- \( x_3 = \frac{1}{2} \left( 5052.624895 + \frac{40401}{5052.624895} \right) = 2528.311474 \)
- Continue this process until the desired accuracy is achieved.
After several iterations, the approximation will converge to the actual square root.
The steps can be summarized in a tabular form:
| Iteration | Approximation |
| 0 | 20200.5 |
| 1 | 10101.249975 |
| 2 | 5052.624895 |
| 3 | 2528.311474 |
The Newton-Raphson method is powerful and converges quickly to the accurate square root, making it suitable for both manual calculations and computer algorithms.

Estimation and Approximation
Estimating and approximating square roots is a useful technique, especially when an exact value is not necessary or when performing mental calculations. Below are detailed steps and methods for estimating and approximating square roots:
- Identify the Perfect Squares
First, identify the perfect squares between which the given number lies. For instance, to estimate the square root of 60:
- The perfect squares closest to 60 are 49 (72) and 64 (82).
- Therefore, \(\sqrt{60}\) is between 7 and 8.
- Linear Approximation
Use linear approximation to find a more accurate estimate. Since 60 is closer to 64 than to 49, we know \(\sqrt{60}\) is closer to 8:
- We can estimate \(\sqrt{60}\) as approximately 7.75 or use more refined methods for better accuracy.
- Averaging Method
This method involves averaging. For example, to estimate \(\sqrt{23}\):
- 23 is between 16 (42) and 25 (52).
- Start with an average: \(\frac{4 + 5}{2} = 4.5\).
- Refine the estimate: Divide 23 by 4.5 to get approximately 5.11.
- Average again: \(\frac{4.5 + 5.11}{2} \approx 4.8\).
- Using Calculator
For quick and more precise approximations, a calculator can be used. For instance:
- To find \(\sqrt{5}\), enter it into the calculator to get approximately 2.236.
- Round the result to the desired precision, such as 2.24 for two decimal places.
- Formula-Based Approximation
For numbers that are not perfect squares, use the formula \(\sqrt{n} \approx \sqrt{p} + \frac{q}{2\sqrt{p}+1}\), where \(p\) is the nearest perfect square less than \(n\) and \(q\) is the difference \(n - p\).
- For example, to estimate \(\sqrt{968}\):
- Nearest perfect square is 961 (312).
- \(\sqrt{968} \approx 31 + \frac{7}{2 \cdot 31 + 1} \approx 31 + \frac{7}{63} \approx 31.11\).
Each of these methods provides a useful approach to estimating square roots, with varying levels of complexity and precision.
Mathematical Tables
Mathematical tables for squares and square roots provide a quick reference to find the square roots of larger numbers. These tables list the squares of numbers and their corresponding square roots, allowing for easy lookup and cross-referencing. Below is an example table that includes squares and square roots for numbers from 1 to 20:
| Number | Square | Square Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
Using these tables, you can quickly determine that the square root of 16 is 4, the square root of 81 is 9, and so on. For numbers not listed in the table, you can use interpolation to estimate the square root or use a calculator for more precision.
Such tables are especially useful for educational purposes and for quick mental calculations without the need for a calculator.
Algorithms for Big Numbers
Calculating the square root of very large numbers requires efficient algorithms, especially when precision and speed are crucial. Below are some advanced algorithms and methods commonly used:
Newton-Raphson Method
The Newton-Raphson method is an iterative numerical method used for finding successively better approximations to the roots (or zeroes) of a real-valued function. When applied to square roots, the iteration formula is:
$$ x_{k+1} = \frac{1}{2} \left( x_k + \frac{N}{x_k} \right) $$
Where \( x_k \) is the current approximation, and \( N \) is the number whose square root is to be found. This method converges quadratically, meaning the number of correct digits roughly doubles with each iteration.
Fast Inverse Square Root Method
This method is used to calculate \( \frac{1}{\sqrt{N}} \) very efficiently, which can then be used to find \( \sqrt{N} \) by multiplying the inverse square root by \( N \). The algorithm, made famous by its use in computer graphics, involves bit-level manipulations and approximations:
$$ y = N \cdot 0.5 $$
$$ i = \text{bit-level representation of } N $$
$$ i = 0x5f3759df - (i >> 1) $$
$$ N = \text{bit-level representation of } i $$
$$ N = N \cdot (1.5 - y \cdot N \cdot N) $$
This method is extremely fast and provides a good initial approximation for iterative refinement.
Binary Search Method
The binary search algorithm can be adapted to find the square root of a number by iteratively narrowing the range in which the square root lies. The steps are:
- Initialize low to 0 and high to the number \( N \).
- Compute the midpoint \( mid = \frac{low + high}{2} \).
- If \( mid^2 \) is close enough to \( N \), return \( mid \).
- If \( mid^2 < N \), set \( low = mid \). Otherwise, set \( high = mid \).
- Repeat steps 2-4 until the desired precision is achieved.
Digit-by-Digit Calculation
This is an old method resembling long division, where the square root is built one digit at a time. It’s especially useful for manual calculations and has a well-defined step-by-step process:
- Pair the digits of the number from right to left.
- Find the largest number whose square is less than or equal to the leftmost pair.
- Subtract the square of this number from the leftmost pair and bring down the next pair of digits.
- Double the current result and determine the next digit that fits the new number formed.
- Repeat until all pairs of digits have been processed.
Continued Fractions
Continued fractions can be used to generate increasingly accurate approximations of square roots. The general form of the continued fraction for \( \sqrt{N} \) is:
$$ \sqrt{N} = a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \cdots}}} $$
Where \( a_i \) are integers determined by the continued fraction expansion process. This method provides highly accurate results and is useful for both theoretical and computational purposes.
Each of these algorithms has its strengths and is suitable for different applications, whether for manual calculations, computer graphics, or high-precision computational tasks.
Examples and Practice Problems
Example 1: Finding the Square Root of 7056
To find the square root of 7056, we can use the estimation and approximation method:
- Consider the unit digit which is 6. Possible square roots ending with 6 are 4 and 6 (since \(4^2 = 16\) and \(6^2 = 36\)).
- Now, consider the first two digits which are 70. This lies between \(8^2 = 64\) and \(9^2 = 81\).
- Assume the tens digit is 8, giving possible roots as 84 and 86.
- Since 84 x 86 is slightly less than 7056, the square root of 7056 is closer to 84.
- Therefore, \(\sqrt{7056} = 84\).
Example 2: Finding the Square Root of 40401
Using a similar method, let's find the square root of 40401:
- Pair the digits from right to left: 404 01.
- The unit digit is 1, so possible square roots end in 1 or 9. Here, the tens digit analysis will help us find the exact root.
- The first three digits are 404, which lies between \(20^2 = 400\) and \(21^2 = 441\).
- Since 404 is closer to 400, the tens digit will be 20.
- Thus, \(\sqrt{40401} = 201\).
Example 3: Using Long Division to Find the Square Root of 68
The long division method provides a systematic way to find square roots:
- Start by grouping the digits in pairs from the decimal point. For 68, group as 68.00.
- Find the largest number whose square is less than or equal to the first group. Here, 8 is the largest number since \(8^2 = 64\).
- Subtract \(64\) from \(68\), bringing down the next pair (00), resulting in 400.
- Double the number already found (8) and determine the next digit. Here, it becomes 16x ≤ 400 where x is the largest possible digit.
- The closest value is 4, giving us 84.
- Thus, the approximate square root of 68 is 8.4.
Example 4: Determining the Least Number to Subtract to Form a Perfect Square
Given a number, find the smallest subtraction to make it a perfect square:
- Consider the number 70.
- The nearest perfect squares are \(64\) (82) and \(81\) (92).
- Since \(70\) is closer to \(64\), subtract \(70 - 64 = 6\).
- Therefore, subtracting \(6\) from \(70\) results in the perfect square \(64\).
Practice solving these problems using the methods described to improve your understanding of finding square roots of large numbers.

Applications
Square roots play a significant role in various fields, aiding in calculations and problem-solving across different applications. Here are some detailed examples:
- Scientific Computations
In science, square roots are often used in statistical calculations, such as determining the standard deviation, which measures the amount of variation or dispersion in a set of values. The formula for the standard deviation \( \sigma \) is:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \( N \) is the number of data points, \( x_i \) are the data points, and \( \mu \) is the mean of the data. - Engineering Problems
Square roots are used in various engineering applications, such as calculating the stresses and strains on materials. For instance, in structural engineering, the Pythagorean theorem helps determine the lengths of components in trusses and beams. The formula for the length \( c \) of the hypotenuse in a right triangle with legs \( a \) and \( b \) is:
\[
c = \sqrt{a^2 + b^2}
\] - Financial Modeling
In finance, square roots are used in the calculation of volatility, which is a measure of the price variation of a financial instrument over time. The formula for volatility \( \sigma \) of a set of returns \( R \) over \( N \) periods is:
\[
\sigma = \sqrt{\frac{\sum_{i=1}^{N} (R_i - \bar{R})^2}{N}}
\]
where \( \bar{R} \) is the average return. - Cryptography
In cryptography, square roots are used in various algorithms, including those related to encryption and decryption processes. For example, the RSA encryption algorithm involves operations with large prime numbers and their roots. Calculating modular square roots is essential in some encryption schemes.
- Distance Calculations
Square roots are fundamental in calculating distances in both two-dimensional and three-dimensional space. For two points \((x_1, y_1)\) and \((x_2, y_2)\) in 2D space, the distance \( D \) is:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]For three points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\) in 3D space, the distance \( D \) is:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\] - Quadratic Equations
Square roots are crucial for solving quadratic equations, which are in the form \( ax^2 + bx + c = 0 \). The quadratic formula for the roots is:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
where the term under the square root, \( b^2 - 4ac \), is called the discriminant and determines the nature of the roots.
Hướng dẫn cách tìm căn bậc hai của các số lớn một cách nhẩm, giúp bạn nhanh chóng và dễ dàng tính toán mà không cần đến máy tính.
Cách Tìm Căn Bậc Hai của Các Số Lớn Một Cách Nhẩm
READ MORE:
Hướng dẫn chi tiết cách tính căn bậc hai của số lớn bằng phương pháp thủ công mà không cần sử dụng máy tính, giúp bạn nắm vững kỹ thuật tính toán này.
Cách Tính Căn Bậc Hai của Số Lớn Thủ Công (Không cần máy tính)