Topic simplify square root of 80: Unlock the mystery of simplifying the square root of 80 with our easy step-by-step guide. Whether you're a student or a math enthusiast, this article will help you break down the process, making it simple and understandable. Dive in and learn how to transform the square root of 80 into its simplest form effortlessly!
Table of Content
- Simplifying the Square Root of 80
- Introduction
- Understanding Square Roots
- Basic Factorization Techniques
- Step-by-Step Simplification of Square Root of 80
- Prime Factorization Method
- Using Exponents to Simplify
- Simplifying Non-Perfect Squares
- Common Mistakes to Avoid
- Practical Applications of Square Roots
- Advanced Simplification Techniques
- Frequently Asked Questions (FAQs)
- Additional Resources and References
- YOUTUBE: Xem video về cách đơn giản hóa căn bậc hai của 80 để hiểu rõ hơn về chủ đề này.
Simplifying the Square Root of 80
To simplify the square root of 80, we need to factorize 80 and look for perfect squares.
Step-by-Step Process
- Factorize 80 into its prime factors:
- 80 = 2 × 40
- 40 = 2 × 20
- 20 = 2 × 10
- 10 = 2 × 5
- Rewrite the square root of 80 using these factors:
\(\sqrt{80} = \sqrt{2^4 \times 5}\)
- Separate the factors under the square root:
\(\sqrt{80} = \sqrt{2^4} \times \sqrt{5}\)
- Simplify the perfect square \(\sqrt{2^4}\):
\(\sqrt{2^4} = \sqrt{16} = 4\)
- Combine the simplified part with the remaining factor:
\(\sqrt{80} = 4 \sqrt{5}\)
Conclusion
Thus, the simplified form of the square root of 80 is:
READ MORE:
Introduction
Simplifying square roots is a fundamental skill in mathematics that allows us to express a square root in its simplest form. In this guide, we will focus on the process of simplifying the square root of 80. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 80 can be written as √80.
To simplify the square root of 80, we aim to express it in its simplest radical form. This involves breaking down the number into its prime factors and simplifying the expression under the radical sign. By the end of this section, you will have a clear understanding of how to simplify √80 using various mathematical techniques.
Let's begin by examining the basic concept of square roots and then proceed to apply these concepts to simplify √80 effectively. The steps involved in the simplification process will be explained in detail, ensuring a comprehensive understanding of each stage.
Through this guide, we will cover the following key aspects:
- Understanding the concept of square roots
- Basic factorization techniques
- Prime factorization method
- Using exponents to simplify square roots
- Common mistakes to avoid during simplification
- Practical applications of simplified square roots
By mastering these techniques, you will be well-equipped to simplify not just √80, but any non-perfect square root you encounter. Let's dive in and simplify the square root of 80 step-by-step!
Understanding Square Roots
Square roots are a fundamental concept in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3, because \(3 \times 3 = 9\).
The symbol for the square root is called a radical sign, represented as \( \sqrt{} \). For example, the square root of 80 is written as \( \sqrt{80} \).
To simplify square roots, particularly those that are not perfect squares, we follow a series of steps:
- Identify the factors of the number under the radical. For 80, the factors are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
- Find the largest perfect square factor of the number. The largest perfect square factor of 80 is 16.
- Rewrite the square root in terms of the largest perfect square factor. For 80, we rewrite it as \( \sqrt{80} = \sqrt{16 \times 5} \).
- Separate the square root of the perfect square from the remaining factor: \( \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} \).
- Simplify the square root of the perfect square. Since \( \sqrt{16} = 4 \), we have \( 4\sqrt{5} \).
Therefore, the simplified form of \( \sqrt{80} \) is \( 4\sqrt{5} \).
This method is useful for simplifying non-perfect squares and helps in making further calculations easier.
Basic Factorization Techniques
Factorization is a fundamental technique in simplifying square roots. It involves breaking down a number into its prime factors. This method is particularly useful for simplifying square roots of non-perfect squares. Here, we will go through the steps to simplify the square root of 80 using basic factorization techniques.
- Identify the Factors:
First, list all the factors of 80. These are numbers that can be multiplied together to equal 80:
- 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
- Find Perfect Squares:
Next, identify which of these factors are perfect squares. A perfect square is a number that can be expressed as the product of an integer with itself:
- 1, 4, 16
- Divide by the Largest Perfect Square:
Divide 80 by the largest perfect square identified in the previous step. In this case, the largest perfect square factor of 80 is 16:
\( 80 \div 16 = 5 \)
- Express as a Product:
Rewrite the original square root as the product of the square roots of the perfect square and the remaining factor:
\( \sqrt{80} = \sqrt{16 \times 5} \)
Using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{80} = \sqrt{16} \times \sqrt{5} \)
- Calculate the Square Root of the Perfect Square:
The square root of 16 is 4, so we can simplify the expression further:
\( \sqrt{16} \times \sqrt{5} = 4\sqrt{5} \)
- Final Simplified Form:
Thus, the square root of 80 simplified using basic factorization techniques is:
\( \sqrt{80} = 4\sqrt{5} \)
This method highlights the importance of recognizing perfect squares and utilizing the property of square roots to simplify expressions efficiently. With practice, these steps can be applied to simplify the square roots of various non-perfect square numbers.
Step-by-Step Simplification of Square Root of 80
In this section, we will simplify the square root of 80 step by step using factorization techniques. The goal is to express the square root in its simplest radical form.
-
List the Factors:
First, list the factors of 80:
- 1
- 2
- 4
- 5
- 8
- 10
- 16
- 20
- 40
- 80
-
Identify Perfect Squares:
From the list of factors, identify the perfect squares:
- 1
- 4
- 16
-
Divide by the Largest Perfect Square:
Divide 80 by the largest perfect square identified, which is 16:
\[ \frac{80}{16} = 5 \]
-
Calculate the Square Root:
Calculate the square root of 16:
\[ \sqrt{16} = 4 \]
-
Combine the Results:
Combine the results to express the square root of 80 in its simplest form:
\[ \sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4\sqrt{5} \]
Therefore, the simplified form of the square root of 80 is \(4\sqrt{5}\).
For further verification, you can convert this to decimal form:
\[ 4\sqrt{5} \approx 4 \times 2.236 = 8.944 \]

Prime Factorization Method
The prime factorization method is a systematic approach to simplify square roots by breaking down the number into its prime factors. Here is the step-by-step process to simplify the square root of 80 using this method:
- Prime Factorization: Find the prime factors of 80.
80 can be factorized as:
80 = 2 × 2 × 2 × 2 × 5
- Pair the Prime Factors: Group the prime factors into pairs.
80 = (2 × 2) × (2 × 2) × 5
- Extract the Square Roots: For each pair of identical factors, take one factor out of the square root.
√80 = √((2 × 2) × (2 × 2) × 5) = 2 × 2 × √5
- Simplify: Multiply the factors outside the square root.
2 × 2 × √5 = 4√5
Thus, the simplified form of √80 is 4√5.
Using Exponents to Simplify
Simplifying square roots using exponents involves leveraging the properties of exponents to break down the radicand into manageable parts. This method can make the simplification process more intuitive, especially for those familiar with exponent rules.
To simplify the square root of 80 using exponents, follow these steps:
-
First, express 80 as a product of its prime factors:
\[ 80 = 2^4 \times 5 \] -
Apply the square root to each factor individually:
\[ \sqrt{80} = \sqrt{2^4 \times 5} \] -
Use the property of square roots that allows you to separate the product of the square roots:
\[ \sqrt{2^4 \times 5} = \sqrt{2^4} \times \sqrt{5} \] -
Since \(2^4\) is a perfect square, simplify \( \sqrt{2^4} \):
\[ \sqrt{2^4} = 2^2 = 4 \] -
Combine the simplified parts:
\[ \sqrt{80} = 4 \sqrt{5} \]
Thus, using exponents, we have simplified \( \sqrt{80} \) to \( 4 \sqrt{5} \). This method highlights the power of exponents in breaking down complex radicands into simpler forms, making the simplification process straightforward and efficient.
Simplifying Non-Perfect Squares
When dealing with non-perfect squares, the process of simplification involves breaking down the number under the square root into its prime factors and identifying perfect squares within those factors. Here is a detailed step-by-step method to simplify non-perfect squares:
-
Find the Prime Factors: Start by finding the prime factors of the number inside the square root. For example, to simplify \( \sqrt{80} \), we find the prime factors of 80:
- 80 can be factored into \( 2^4 \times 5 \)
-
Identify Perfect Squares: Next, look for perfect square factors within the prime factors. In our example, \( 2^4 \) is a perfect square (since \( 2^4 = (2^2)^2 \)).
-
Rewrite the Expression: Rewrite the original square root as a product of square roots of the perfect square factor and the remaining factor:
- \[ \sqrt{80} = \sqrt{2^4 \times 5} \]
-
Simplify: Apply the property that the square root of a product is the product of the square roots:
- \[ \sqrt{80} = \sqrt{(2^2)^2 \times 5} = \sqrt{(2^2)^2} \times \sqrt{5} = 4\sqrt{5} \]
Using this method, we find that \( \sqrt{80} \) simplifies to \( 4\sqrt{5} \). This approach can be applied to any non-perfect square, ensuring that the square root is expressed in its simplest form.
Common Mistakes to Avoid
When simplifying the square root of 80, several common errors can occur. Here are some mistakes to be mindful of and tips on how to avoid them:
- Ignoring Prime Factorization: One common mistake is not breaking down the number into its prime factors. Properly factorizing 80 as \(2^4 \times 5\) helps in simplification.
- Prime factorize 80: \(80 = 2 \times 40 = 2 \times 2 \times 20 = 2 \times 2 \times 2 \times 10 = 2 \times 2 \times 2 \times 2 \times 5 = 2^4 \times 5\).
- Incorrectly Grouping Factors: When using the prime factorization method, it is crucial to group the factors correctly. Remember to pair identical factors.
- Identify pairs: From \(2^4 \times 5\), you can group \(2^2\) pairs, which results in \(2 \times 2\).
- Simplify: \(2 \times 2 \times \sqrt{5} = 4\sqrt{5}\).
- Leaving Unpaired Factors Under the Root: Some learners forget to take out all possible pairs from under the square root, leaving unnecessary factors inside.
- Ensure all pairs are considered: After taking out the pairs \(2 \times 2\), the correct simplification is \(4\sqrt{5}\), not \(2\sqrt{20}\) or \(8\sqrt{2.5}\).
- Overlooking Perfect Squares: Recognize that part of the factorization may include a perfect square.
- Example: If simplifying \( \sqrt{80} \), notice that \(80 = 16 \times 5\), where 16 is a perfect square.
- Simplify: \( \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4\sqrt{5}\).
- Calculation Errors: Incorrect arithmetic can lead to wrong results.
- Double-check calculations: Verify each step, especially when multiplying or grouping factors.
- Example: Incorrectly stating \(2 \times 2 \times \sqrt{5} = 2\sqrt{10}\) instead of \(4\sqrt{5}\).
- Misinterpreting Simplified Forms: Misunderstanding the final simplified form can cause confusion.
- Correctly interpret: \(4\sqrt{5}\) means \(4 \times \sqrt{5}\), not \(4 \times 5\).
Avoiding these mistakes will help in correctly simplifying the square root of 80 and applying similar techniques to other numbers.
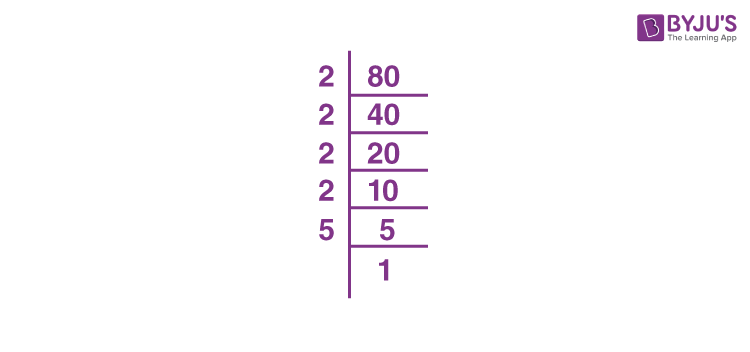
Practical Applications of Square Roots
Square roots have numerous practical applications across various fields, providing valuable insights and solving complex problems. Here are some real-world uses of square roots:
- Geometry and Area Calculations: Square roots are crucial in calculating areas and side lengths of geometric shapes.
- To find the side length of a square given its area \(A\), use the formula \(s = \sqrt{A}\).
- Example: For a square with an area of 80 square units, the side length is \(s = \sqrt{80} = 4\sqrt{5} \approx 8.94\) units.
- Physics and Engineering: In physics, square roots are often used to solve equations involving quadratic relationships.
- For instance, in the equation \(v = \sqrt{2gh}\) where \(v\) is velocity, \(g\) is acceleration due to gravity, and \(h\) is height, square roots help in determining the final velocity of an object in free fall.
- Example: If \(h = 80\) meters and \(g = 9.8 \, \text{m/s}^2\), then \(v = \sqrt{2 \times 9.8 \times 80} \approx 39.6 \, \text{m/s}\).
- Finance: Square roots are used in calculating various financial metrics, including standard deviation and volatility in risk assessments.
- Standard deviation, a measure of investment risk, often involves square root calculations of variance. The formula is \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \bar{x})^2} \).
- Example: For an investment with a variance of 80, the standard deviation \( \sigma = \sqrt{80} \approx 8.94 \).
- Statistics: In statistics, square roots play a role in calculating root mean square (RMS) values, a measure of the magnitude of a set of numbers.
- The RMS is given by \( \text{RMS} = \sqrt{\frac{1}{N}\sum_{i=1}^{N}x_i^2} \), useful in data analysis to understand variability.
- Example: For data points {9, 16, 25, 36}, the RMS is \( \text{RMS} = \sqrt{\frac{1}{4}(9 + 16 + 25 + 36)} = \sqrt{21.5} \approx 4.64 \).
- Computer Graphics: Square roots are integral in calculating distances and scaling in graphics rendering.
- In 3D graphics, the distance between two points \((x_1, y_1, z_1)\) and \((x_2, y_2, z_2)\) is calculated using \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \).
- Example: For points (1, 2, 3) and (4, 6, 8), the distance is \( d = \sqrt{(4-1)^2 + (6-2)^2 + (8-3)^2} = \sqrt{9 + 16 + 25} = \sqrt{50} \approx 7.07 \).
Understanding and applying square roots enable problem-solving in these diverse fields, showcasing their importance in practical scenarios.
Advanced Simplification Techniques
When it comes to simplifying square roots, there are several advanced techniques that can be applied to ensure accuracy and efficiency. These methods build on the basic understanding of square roots and factorization. Below, we delve into some of these techniques:
1. Simplifying Using the Difference of Squares
The difference of squares is a useful algebraic identity that can simplify certain square root expressions. The identity is given by:
\[
a^2 - b^2 = (a + b)(a - b)
\]
To use this identity in simplifying the square root of a number, you look for two perfect squares whose difference is the number under the square root. For example, if we consider \(\sqrt{80}\), we look for two perfect squares such that:
\[
80 = a^2 - b^2
\]
However, in this case, since 80 is not expressible as a difference of two perfect squares, this technique isn't directly applicable. Nonetheless, understanding this concept is beneficial for other complex simplifications.
2. Simplifying Using Rationalizing Techniques
Rationalizing involves eliminating the square root from the denominator of a fraction. This technique is particularly useful in algebra and higher mathematics.
For example, consider the expression \(\frac{1}{\sqrt{80}}\). To rationalize the denominator, multiply both the numerator and the denominator by \(\sqrt{80}\):
\[
\frac{1}{\sqrt{80}} \times \frac{\sqrt{80}}{\sqrt{80}} = \frac{\sqrt{80}}{80}
\]
Next, simplify \(\sqrt{80}\) as discussed in previous sections:
\[
\sqrt{80} = \sqrt{16 \times 5} = 4\sqrt{5}
\]
Therefore:
\[
\frac{\sqrt{80}}{80} = \frac{4\sqrt{5}}{80} = \frac{\sqrt{5}}{20}
\]
3. Simplifying by Substitution Method
In some complex scenarios, substitution can simplify the process. If dealing with a more complex expression involving square roots, substituting a variable for the square root can help. For example:
Given \(x = \sqrt{80}\), we can square both sides to get:
\[
x^2 = 80
\]
This substitution can simplify algebraic manipulation, especially in equations or functions involving \(\sqrt{80}\).
4. Advanced Use of Prime Factorization
Prime factorization is a fundamental technique but can be extended for more complex expressions. By breaking down the number into its prime factors, deeper insights can be gained. For \(\sqrt{80}\):
\[
80 = 2^4 \times 5
\]
Applying the square root gives:
\[
\sqrt{80} = \sqrt{2^4 \times 5} = \sqrt{2^4} \times \sqrt{5} = 4\sqrt{5}
\]
This method is particularly powerful when dealing with larger numbers or variables.
5. Using Calculators and Software
For very complex square roots, leveraging technology can be advantageous. Advanced calculators and mathematical software (like WolframAlpha or MATLAB) can handle intricate calculations and provide precise results, saving time and reducing errors.
These advanced techniques enhance your ability to simplify square roots accurately and efficiently, especially in more challenging mathematical problems.
Frequently Asked Questions (FAQs)
Here are some frequently asked questions about simplifying the square root of 80:
-
What is the square root of 80 in its simplest form?
To simplify √80, we can break it down using its prime factors. √80 = √(16 × 5) = 4√5.
-
How do you simplify √80 using prime factorization?
Start by finding the prime factors of 80, which are 2 and 5. Then, rewrite √80 as √(16 × 5) = 4√5.
-
Can the square root of 80 be simplified further?
No, 4√5 is already in its simplest radical form because 5 is not a perfect square.
-
What are some common mistakes when simplifying √80?
One common mistake is not properly factorizing 80, leading to incorrect simplification. It's important to correctly identify and use the prime factors.
-
Are there real-world applications for understanding how to simplify square roots?
Yes, simplifying square roots is used in various fields such as engineering, physics, and computer science for calculations involving areas, volumes, and more complex formulas.
Additional Resources and References

Xem video về cách đơn giản hóa căn bậc hai của 80 để hiểu rõ hơn về chủ đề này.
How to Simplify the Square Root of 80: sqrt(80) | Làm thế nào để đơn giản hóa căn bậc hai của 80
READ MORE:
Xem video về cách đơn giản hóa căn bậc hai của số 80 bằng cách sử dụng cây phân tích yếu tố để hiểu rõ hơn về chủ đề này.
Simplifying the Square Root of a Number Using a Factor Tree, Sqrt(80) | Đơn giản hóa căn bậc hai của một số bằng cách sử dụng cây phân tích yếu tố, Sqrt(80)