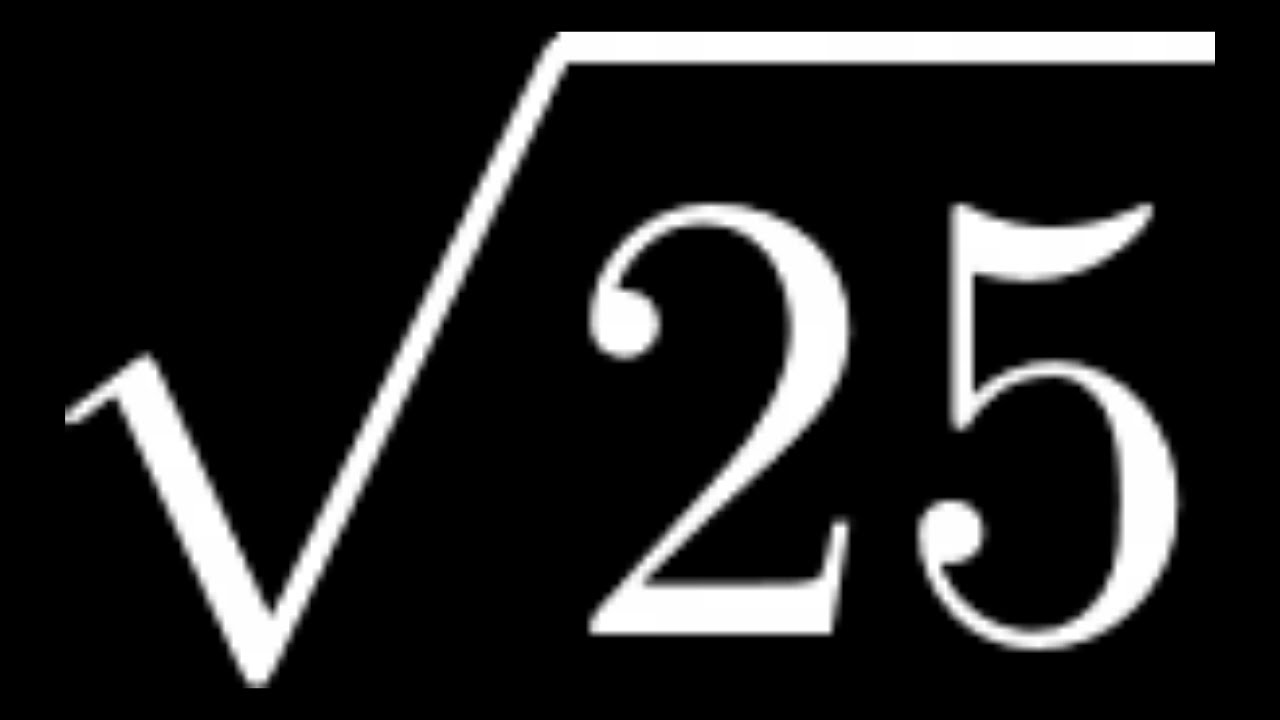Topic simplify square root of 5: Simplifying the square root of 5 may seem challenging, but with our step-by-step guide, you'll master it in no time. This article will walk you through the process, highlight common mistakes, and provide practical examples to help you understand and apply this fundamental mathematical concept with confidence.
Table of Content
- Search Results for "simplify square root of 5" on Bing
- Introduction to Square Roots
- Understanding the Square Root of 5
- Properties of the Square Root of 5
- Step-by-Step Guide to Simplifying the Square Root of 5
- Common Mistakes to Avoid
- Applications of the Square Root of 5 in Mathematics
- Practice Problems and Solutions
- Advanced Simplification Techniques
- Conclusion and Summary
- Additional Resources and References
- YOUTUBE: Khám phá cách đơn giản hóa căn bậc hai của 5 với hướng dẫn chi tiết và dễ hiểu trong video này.
Search Results for "simplify square root of 5" on Bing
Here is a summary of the search results for the keyword "simplify square root of 5" on Bing:
Web Results:
- Mathematical explanations and tutorials on simplifying the square root of 5.
- Online calculators and tools for calculating and simplifying square roots.
- Educational articles and forums discussing the concept of square roots and their simplification.
Images:
- Visual representations of square roots and mathematical symbols.
- Illustrations and diagrams explaining the concept of square root of 5.
News:
- No specific news articles were found related to "simplify square root of 5."
Related Searches:
- Other related searches include "simplify square root of 5 calculator" and "how to simplify square root of 5 step by step."

READ MORE:
Introduction to Square Roots
Square roots are mathematical expressions that represent a value which, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \( 3 \times 3 = 9 \). Square roots are denoted by the radical symbol \( \sqrt{} \).
Understanding square roots is fundamental in mathematics, especially in algebra and geometry. Here are some key points to consider:
- The square root of a number \( x \) is written as \( \sqrt{x} \).
- Square roots can be positive or negative, but we often refer to the positive (principal) square root.
- Perfect squares are numbers whose square roots are integers (e.g., 1, 4, 9, 16).
- Non-perfect squares have square roots that are irrational numbers, meaning they cannot be expressed as a simple fraction.
For example, the square root of 5 is an irrational number because it cannot be simplified to a fraction and its decimal representation is non-repeating and non-terminating. The approximate value is:
\[
\sqrt{5} \approx 2.236
\]
Calculating square roots can be done through various methods such as factorization, using the long division method, or by employing a calculator for more complex numbers.
Below is a simple example table of perfect squares and their roots:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
By understanding the basics of square roots, we can proceed to more complex operations like simplifying the square root of non-perfect squares, such as 5.
Understanding the Square Root of 5
The square root of 5 is an irrational number, which means it cannot be exactly expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate value of the square root of 5 is:
\[
\sqrt{5} \approx 2.236
\]
To understand why \( \sqrt{5} \) is irrational, let's break it down step by step:
- Definition of Irrational Numbers:
An irrational number cannot be written as a ratio of two integers. Its decimal form goes on forever without repeating.
- Prime Factorization:
First, consider the number 5. Since it is a prime number, its only factors are 1 and 5. Therefore, it cannot be simplified further into smaller square roots.
- Square Root Properties:
When we take the square root of a prime number (such as 5), the result is always irrational. This is because there are no two identical factors of a whole number that multiply together to give 5.
- Approximation:
Although we can't simplify \( \sqrt{5} \) into a fraction, we can approximate its value using long division or a calculator. As mentioned, \( \sqrt{5} \approx 2.236 \). This approximation helps us understand its magnitude and use it in practical calculations.
Here's a table comparing the square roots of some common numbers, including 5:
| Number | Square Root |
| 2 | \(\approx 1.414\) |
| 3 | \(\approx 1.732\) |
| 4 | 2 |
| 5 | \(\approx 2.236\) |
| 6 | \(\approx 2.449\) |
Understanding that the square root of 5 is irrational helps in various mathematical contexts, from solving equations to geometry, where precise values are essential. Embracing its irrational nature allows us to work with approximations and recognize patterns in mathematical calculations.
Properties of the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), has several unique properties that distinguish it from both rational and other irrational numbers. Understanding these properties provides a deeper insight into its mathematical significance.
- Irrational Number:
\( \sqrt{5} \) is an irrational number, which means it cannot be expressed as a simple fraction. Its decimal form is non-repeating and non-terminating:
\[
\sqrt{5} \approx 2.23606797749979...
\] - Non-Perfect Square:
Since 5 is not a perfect square, \( \sqrt{5} \) cannot be simplified into an integer or a simple fraction. This distinguishes it from numbers like 4 and 9, whose square roots are 2 and 3, respectively.
- Algebraic Properties:
- Addition and Subtraction:
The sum or difference of \( \sqrt{5} \) with a rational number remains irrational. For example, \( 2 + \sqrt{5} \) and \( 3 - \sqrt{5} \) are both irrational numbers.
- Multiplication and Division:
Multiplying or dividing \( \sqrt{5} \) by a rational number results in an irrational number. For example, \( 2 \cdot \sqrt{5} = 2\sqrt{5} \) and \( \sqrt{5} / 2 = \frac{\sqrt{5}}{2} \) are both irrational.
- Exponentiation:
When squared, \( \sqrt{5} \) returns the original number: \( (\sqrt{5})^2 = 5 \).
- Addition and Subtraction:
- Geometric Interpretation:
In geometry, \( \sqrt{5} \) can represent the length of the diagonal of a rectangle with sides of length 1 and 2. Using the Pythagorean theorem:
\[
\sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\] - Continued Fraction Representation:
\( \sqrt{5} \) can be expressed as a continued fraction, which provides an infinite series representation:
\[
\sqrt{5} = 2 + \cfrac{1}{4 + \cfrac{1}{4 + \cfrac{1}{4 + \ddots}}}
\]
These properties highlight the complexity and utility of \( \sqrt{5} \) in various mathematical contexts, from algebraic equations to geometric constructions, making it a fundamental concept worth mastering.
Step-by-Step Guide to Simplifying the Square Root of 5
Simplifying the square root of 5 involves expressing it in the simplest radical form. Here is a detailed step-by-step guide:
- Identify the Number:
The number we need to simplify is 5, which is a prime number. This means it cannot be factored into smaller integers other than 1 and itself.
- Express in Radical Form:
The square root of 5 is already in its simplest radical form as √5 because it cannot be simplified further.
- Understand the Concept:
For non-prime numbers, you would factorize them into smaller numbers. For example, √12 can be written as √(4×3), which simplifies to 2√3 since 4 is a perfect square.
- Example of a Prime Number:
Since 5 is prime, √5 does not simplify further. Unlike composite numbers, prime numbers have no additional factors to simplify.
- Verification:
You can use a calculator to check that √5 approximately equals 2.236, and this value cannot be simplified into a product of simpler square roots.
While √5 is already simplified, understanding this process helps in handling other square roots effectively.
Here are some additional examples for practice:
- Simplify √18: √18 = √(9×2) = 3√2
- Simplify √20: √20 = √(4×5) = 2√5
By following these steps, you can simplify square roots efficiently. Keep practicing with different numbers to become more comfortable with the process.

Common Mistakes to Avoid
When simplifying the square root of 5 or any other square root, there are several common mistakes to be aware of. Avoiding these errors will help ensure your calculations are accurate and efficient.
- Incorrect Factorization: When simplifying square roots, it is crucial to factorize the number inside the radical correctly. Incorrect factorization can lead to wrong simplifications. For example, avoid assuming that \( \sqrt{20} = \sqrt{4 \cdot 5} \) can be directly simplified without breaking it down to \( 2\sqrt{5} \).
- Improper Use of Product Rule: The product rule states \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \). Ensure both a and b are nonnegative before applying this rule. Misapplying this rule can lead to incorrect results, especially with negative numbers.
- Ignoring Perfect Squares: Always check if the number inside the radical can be broken down into perfect squares. For example, \( \sqrt{50} \) can be simplified to \( \sqrt{25 \cdot 2} = 5\sqrt{2} \). Ignoring this step can lead to incomplete simplification.
- Misinterpreting the Square Root of a Sum: Remember that \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \). This is a common mistake that leads to incorrect simplifications. For instance, \( \sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16} \); instead, \( \sqrt{25} = 5 \).
- Forgetting to Simplify Completely: After factorizing and applying the square root, ensure that the expression is simplified completely. For example, \( 2\sqrt{12} \) should be further simplified to \( 4\sqrt{3} \).
- Misapplying the Quotient Rule: The quotient rule states \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Be cautious to apply this rule correctly, especially ensuring that b is not zero. Incorrect application can lead to errors in simplification.
By keeping these common mistakes in mind and carefully following the proper steps, you can avoid errors and accurately simplify square roots.
Applications of the Square Root of 5 in Mathematics
The square root of 5 (\(\sqrt{5}\)) has various applications in mathematics and related fields. Here are some significant examples:
Pythagorean Theorem
The square root of 5 frequently appears in problems involving the Pythagorean theorem. For instance, in a right-angled triangle with legs of lengths 1 and 2, the hypotenuse will be \(\sqrt{1^2 + 2^2} = \sqrt{5}\).
Given a right-angled triangle with legs \(a = 1\) and \(b = 2\), calculate the hypotenuse \(c\).
Use the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\).
Substitute the values: \(c = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}\).
Golden Ratio
The golden ratio (\(\phi\)) is another fascinating application of \(\sqrt{5}\). The golden ratio is defined as:
\[
\phi = \frac{1 + \sqrt{5}}{2}
\]
This ratio is prevalent in various fields, including art, architecture, and nature.
Geometry and Algebra
\(\sqrt{5}\) is used in various geometric and algebraic contexts, such as finding the side lengths of certain polygons. For example, a regular pentagon can be constructed using the golden ratio, which involves \(\sqrt{5}\).
In the diagonal of a regular pentagon, the relationship between the side length \(s\) and the diagonal \(d\) is given by:
\[
d = s \cdot \phi = s \cdot \frac{1 + \sqrt{5}}{2}
\]
Physics
Square roots, including \(\sqrt{5}\), appear in various physics formulas. For example, in calculating the time (\(t\)) it takes for an object to fall from a height (\(h\)):
\[
t = \sqrt{\frac{2h}{g}}
\]
Here, \(g\) is the acceleration due to gravity. If \(h\) involves \(\sqrt{5}\), this value will be part of the calculation.
Mathematical Constants and Computation
\(\sqrt{5}\) is utilized in computations involving quadratic equations and roots. For example, in solving the quadratic equation \(x^2 - 5 = 0\), the solutions are \(x = \pm\sqrt{5}\).
Examples
Evaluate \(\sqrt{5}\) in the context of the quadratic equation \(x^2 - 5 = 0\).
Solution: The roots are \(x = \pm\sqrt{5}\).
Practice Problems
Find the hypotenuse of a right-angled triangle with legs 3 and \(\sqrt{5}\).
Use \(\sqrt{5}\) to calculate the length of the diagonal of a rectangle with sides 2 and \(\sqrt{5}\).
Practice Problems and Solutions
Practicing the simplification of square roots helps to solidify the concepts and methods. Below are some problems along with detailed solutions to guide you through the process.
-
Simplify \( \sqrt{20} \)
- Factor 20 into its prime factors: \( 20 = 2^2 \times 5 \)
- Apply the square root to the factors: \( \sqrt{20} = \sqrt{2^2 \times 5} \)
- Separate the perfect square: \( \sqrt{2^2} \times \sqrt{5} \)
- Simplify: \( 2\sqrt{5} \)
Solution: \( 2\sqrt{5} \)
-
Simplify \( \sqrt{50} \)
- Factor 50 into its prime factors: \( 50 = 2 \times 5^2 \)
- Apply the square root to the factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
- Separate the perfect square: \( \sqrt{2} \times \sqrt{5^2} \)
- Simplify: \( 5\sqrt{2} \)
Solution: \( 5\sqrt{2} \)
-
Simplify \( \sqrt{72} \)
- Factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \)
- Apply the square root to the factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
- Separate the perfect square: \( \sqrt{2^2} \times \sqrt{2 \times 3^2} \)
- Simplify: \( 2 \times 3\sqrt{2} \)
- Combine: \( 6\sqrt{2} \)
Solution: \( 6\sqrt{2} \)
-
Simplify \( \sqrt{32} \)
- Factor 32 into its prime factors: \( 32 = 2^5 \)
- Apply the square root to the factors: \( \sqrt{32} = \sqrt{2^5} \)
- Separate the perfect square: \( \sqrt{2^4} \times \sqrt{2} \)
- Simplify: \( 4\sqrt{2} \)
Solution: \( 4\sqrt{2} \)
-
Simplify \( \sqrt{200} \)
- Factor 200 into its prime factors: \( 200 = 2^3 \times 5^2 \)
- Apply the square root to the factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
- Separate the perfect square: \( \sqrt{2^2} \times \sqrt{2 \times 5^2} \)
- Simplify: \( 2 \times 5\sqrt{2} \)
- Combine: \( 10\sqrt{2} \)
Solution: \( 10\sqrt{2} \)
Practice these problems to gain confidence in simplifying square roots. Remember to always look for perfect squares within the number and factor them out step by step.
Advanced Simplification Techniques
When dealing with advanced simplification techniques for square roots, especially non-perfect squares like the square root of 5, it’s essential to apply properties of square roots and factorization methods. Below are detailed techniques to simplify complex square root expressions.
Using the Product Property of Square Roots
The product property states that for any non-negative numbers \(a\) and \(b\):
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
This property can be particularly useful in simplifying square roots involving products of numbers.
Example 1: Simplifying \(\sqrt{50}\)
- First, factor 50 into its prime factors: \(50 = 2 \cdot 5^2\).
- Apply the product property: \(\sqrt{50} = \sqrt{2 \cdot 5^2}\).
- Separate the factors under the square root: \(\sqrt{2} \cdot \sqrt{5^2}\).
- Simplify the perfect square: \(\sqrt{5^2} = 5\).
- Final simplified form: \(5\sqrt{2}\).
Using the Quotient Property of Square Roots
The quotient property states that for any non-negative numbers \(a\) and \(b\) (where \(b \neq 0\)):
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
This property is helpful for simplifying square roots involving fractions.
Example 2: Simplifying \(\sqrt{\frac{45}{5}}\)
- First, simplify the fraction inside the square root: \(\frac{45}{5} = 9\).
- Apply the quotient property: \(\sqrt{\frac{45}{5}} = \sqrt{9}\).
- Simplify the perfect square: \(\sqrt{9} = 3\).
Combining Like Terms
When simplifying expressions involving multiple square roots, combine like terms whenever possible.
Example 3: Simplifying \(2\sqrt{12} + 3\sqrt{3}\)
- Simplify each term: \(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\).
- Rewrite the expression: \(2 \cdot 2\sqrt{3} + 3\sqrt{3}\).
- Combine like terms: \(4\sqrt{3} + 3\sqrt{3} = 7\sqrt{3}\).
Simplifying Higher Powers
For higher powers under the square root, express the radicand as a product of squares and other terms.
Example 4: Simplifying \(\sqrt{x^6y^4}\)
- Rewrite the radicand: \(x^6y^4 = (x^3)^2(y^2)^2\).
- Apply the product property: \(\sqrt{(x^3)^2(y^2)^2} = \sqrt{(x^3)^2} \cdot \sqrt{(y^2)^2}\).
- Simplify the square roots: \(x^3y^2\).
These techniques are essential for handling more complex square root expressions and achieving their simplified forms effectively.
Conclusion and Summary
In this guide, we explored the various aspects of simplifying the square root of 5 and its significance in mathematics. Here's a brief summary of what we covered:
- Introduction to Square Roots: We started with a foundational understanding of square roots, emphasizing their importance in mathematical computations and various real-world applications.
- Understanding the Square Root of 5: We delved into the properties of the square root of 5, noting its irrational nature and its approximate value of 2.236.
- Properties of the Square Root of 5: We examined key properties, including its role in the golden ratio, and how it fits into the broader category of irrational numbers.
- Step-by-Step Guide to Simplifying the Square Root of 5: A detailed walkthrough was provided on how to handle and simplify expressions involving the square root of 5.
- Common Mistakes to Avoid: We highlighted common pitfalls, such as incorrect factorization and misinterpretation of the properties of square roots.
- Applications of the Square Root of 5 in Mathematics: This section covered various applications, from geometry to algebra, and its occurrence in different mathematical contexts.
- Practice Problems and Solutions: We provided a series of problems to practice simplifying square roots, enhancing understanding through hands-on exercises.
- Advanced Simplification Techniques: For those looking to deepen their understanding, we discussed advanced techniques for handling more complex expressions involving square roots.
In conclusion, mastering the simplification of square roots, particularly the square root of 5, is a valuable skill in mathematics. It enhances problem-solving abilities and provides a deeper insight into the nature of numbers. Keep practicing and exploring to further solidify your understanding.
Additional Resources and References
For further reading and more in-depth understanding, consider exploring the following resources:
-
This resource provides a thorough introduction to simplifying square roots, including detailed examples and practice problems.
-
A beginner-friendly guide to understanding square roots, complete with interactive elements and quizzes to test your knowledge.
-
An extensive tutorial on simplifying radicals, with a focus on step-by-step instructions and common pitfalls to avoid.
-
A video tutorial that visually explains the process of simplifying square roots, ideal for visual learners.
-
This lesson covers the basics of simplifying square roots and includes interactive practice problems.
-
An article exploring different techniques for simplifying radicals, providing multiple approaches to suit different learning styles.
For advanced learners seeking to deepen their understanding, the following references are recommended:
-
An in-depth exploration of irrational numbers, including the square root of 5, with historical context and mathematical proofs.
-
A research paper discussing advanced methods for approximating square roots, suitable for those interested in mathematical theory and applications.
These resources will provide comprehensive insights and practice opportunities to help you master the simplification of the square root of 5 and related mathematical concepts.
Khám phá cách đơn giản hóa căn bậc hai của 5 với hướng dẫn chi tiết và dễ hiểu trong video này.
Căn Bậc Hai của 5 Được Đơn Giản Hóa
READ MORE:
Hướng dẫn chi tiết về cách đơn giản hóa căn bậc hai trong video này, giúp bạn nắm vững kiến thức một cách dễ dàng.
Cách Đơn Giản Hóa Căn Bậc Hai